2.6 正多边形与圆 同步练(含答案) 2025-2026学年数学苏科版九年级上册
文档属性
| 名称 | 2.6 正多边形与圆 同步练(含答案) 2025-2026学年数学苏科版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 966.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 23:21:27 | ||
图片预览



文档简介
2.6 正多边形与圆
第1课时 正多边形的有关概念及计算
1. 各边相等、各角也相等的多边形叫做正多边形.
2. 一般地,只要用量角器把一个圆n(n≥3)等分,依次连接各等分点就能得到这个圆的内接正n边形,这个圆是这个正n边形的外接圆.正多边形的外接圆的圆心叫做正多边形的中心,外接圆的半径叫做正多边形的半径.
建议用时:20分钟
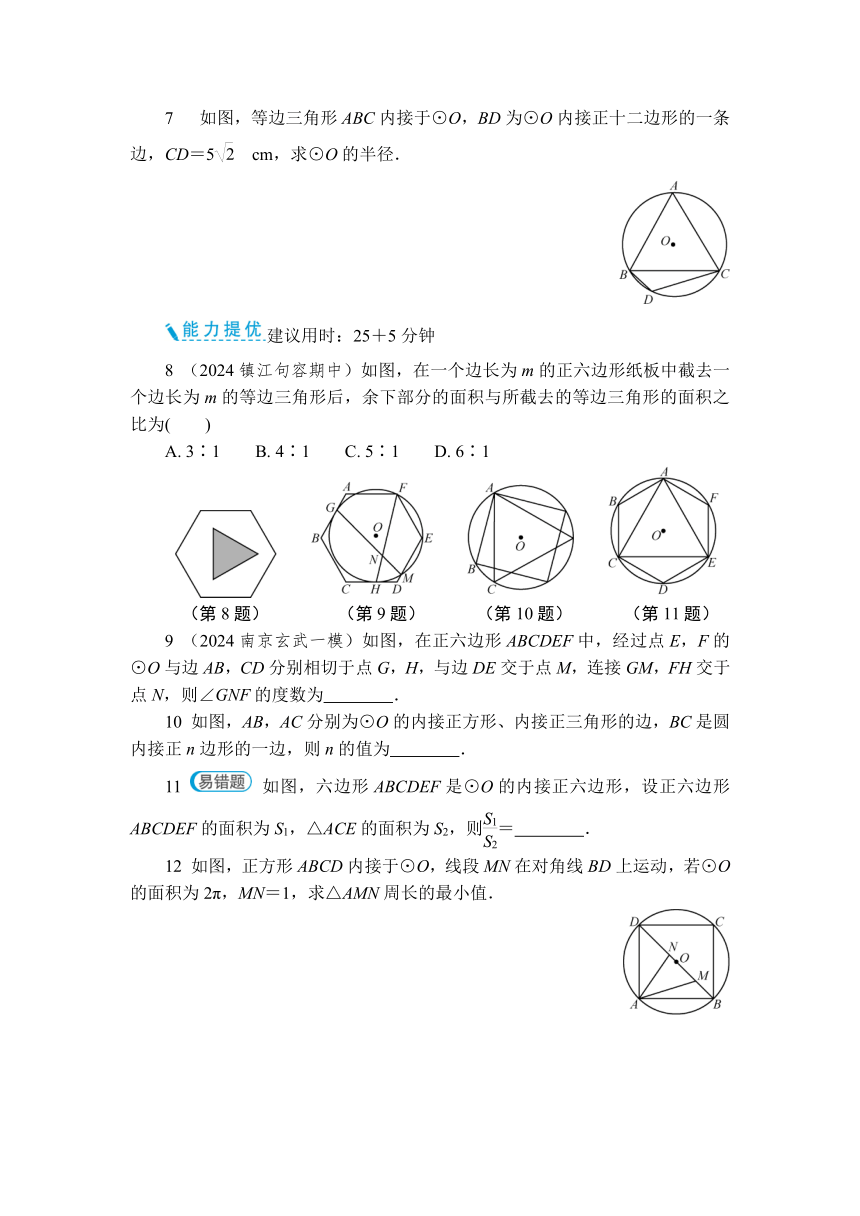
1 (2024济宁)如图,边长为2的正六边形ABCDEF内接于⊙O,则它的内切圆半径为( )
A. 1 B. 2 C. D.
(第1题) (第2题) (第4题) (第5题) (第6题)
2 (2024青岛)为筹备运动会,小松制作了如图所示的宣传牌,在正五边形ABCDE和正方形CDFG中,CF,DG的延长线分别交AE,AB于点M,N,则∠FME的度数是( )
A. 90° B. 99° C. 108° D. 135°
3 (2024南通崇川期中)若正多边形的中心角为30°,则该正多边形的边数为 .
4 (2024镇江)如图,AB是⊙O的内接正n边形的一边,点C在⊙O上,∠ACB=18°,则n= .
5 (2024盐城盐都月考)如图,边长为2的正方形内接于⊙M,则⊙M的半径是 .
6 (2024启东期中)如图,将⊙O的圆周12等分,圆内接矩形ABCD的面积为20,则圆内接正六边形的面积为 .
7 如图,等边三角形ABC内接于⊙O,BD为⊙O内接正十二边形的一条边,CD=5 cm,求⊙O的半径.
建议用时:25+5分钟
8 (2024镇江句容期中)如图,在一个边长为m的正六边形纸板中截去一个边长为m的等边三角形后,余下部分的面积与所截去的等边三角形的面积之比为( )
A. 3∶1 B. 4∶1 C. 5∶1 D. 6∶1
(第8题) (第9题) (第10题) (第11题)
9 (2024南京玄武一模)如图,在正六边形ABCDEF中,经过点E,F的⊙O与边AB,CD分别相切于点G,H,与边DE交于点M,连接GM,FH交于点N,则∠GNF的度数为 .
10 如图,AB,AC分别为⊙O的内接正方形、内接正三角形的边,BC是圆内接正n边形的一边,则n的值为 .
11 如图,六边形ABCDEF是⊙O的内接正六边形,设正六边形ABCDEF的面积为S1,△ACE的面积为S2,则= .
12 如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2π,MN=1,求△AMN周长的最小值.
13 如图,中心为O的正六边形ABCDEF的半径为6 cm,点P,Q同时分别从A,D两点出发,以1 cm/s的速度沿AF,DC向终点F,C运动,连接PB,PE,QB,QE,设运动时间为t s.
(1) 求证:四边形PBQE为平行四边形;
(2) 当四边形PBQE为矩形时,求矩形PBQE的面积与正六边形ABCDEF的面积之比.
第2课时 正多边形的画法及应用
1. 正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都经过正n边形的中心.一个正多边形,如果有偶数条边,那么它既是轴对称图形,又是中心对称图形,对称中心就是这个正多边形的中心.
2. 利用直尺和圆规可以画出圆的内接正多边形.依次连接互相垂直的直径端点所得的四边形是圆的内接正方形;以圆的半径为半径,在圆周上依次截取可得6个等分点,并顺次连接这些等分点所得的多边形是圆的内接正六边形.
建议用时:20分钟
1 下列说法中,错误的是( )
A. 正多边形的每个内角都相等 B. 正多边形都是轴对称图形
C. 正多边形都是中心对称图形 D. 正多边形的中心到各边的距离相等
2 如图所示的向日葵图案是用等分圆周画出的,则⊙O的半径与半圆P半径的比为( )
A. 2∶1 B. 4∶1 C. 3∶1 D. 5∶3
(第2题) (第3题) (第4题) (第5题)
3 (2024盐城期中)正六边形蜂巢的建筑结构密合度最高、用材最少、空间最大、也最为坚固.如图,某蜂巢的房孔是边长为6的正六边形ABCDEF,点O是正六边形的中心,则BF的长为( )
A. 12 B. 6 C. 6 D. 12
4 如图,在正五边形ABCDE中,经过C,D两点的⊙O与AB,AE分别相切于点M,N,连接CM,CN,则∠MCN= .
5 如图,在正十边形A1A2A3A4A5A6A7A8A9A10中,连接A1A4,A1A7,则∠A4A1A7= .
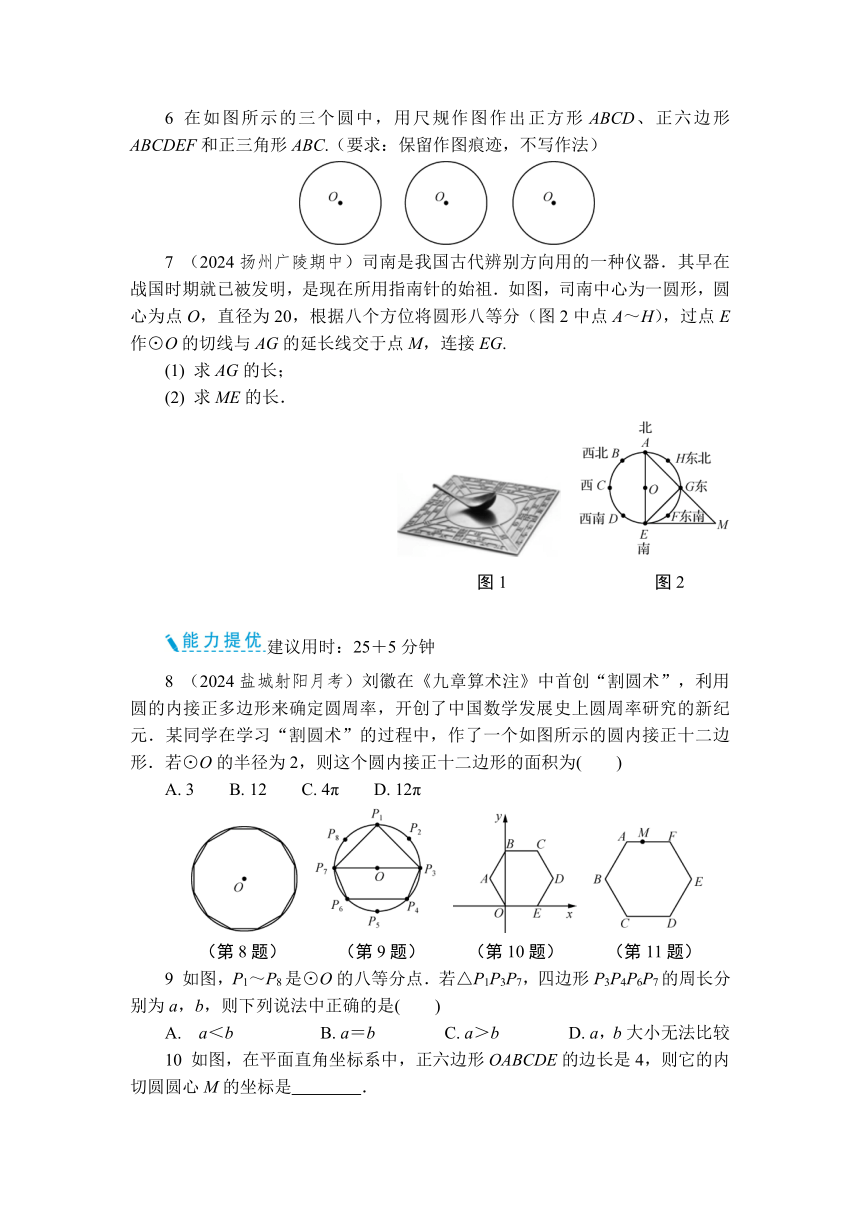
6 在如图所示的三个圆中,用尺规作图作出正方形ABCD、正六边形ABCDEF和正三角形ABC.(要求:保留作图痕迹,不写作法)
7 (2024扬州广陵期中)司南是我国古代辨别方向用的一种仪器.其早在战国时期就已被发明,是现在所用指南针的始祖.如图,司南中心为一圆形,圆心为点O,直径为20,根据八个方位将圆形八等分(图2中点A~H),过点E作⊙O的切线与AG的延长线交于点M,连接EG.
(1) 求AG的长;
(2) 求ME的长.
图1 图2
建议用时:25+5分钟
8 (2024盐城射阳月考)刘徽在《九章算术注》中首创“割圆术”,利用圆的内接正多边形来确定圆周率,开创了中国数学发展史上圆周率研究的新纪元.某同学在学习“割圆术”的过程中,作了一个如图所示的圆内接正十二边形.若⊙O的半径为2,则这个圆内接正十二边形的面积为( )
A. 3 B. 12 C. 4π D. 12π
(第8题) (第9题) (第10题) (第11题)
9 如图,P1~P8是⊙O的八等分点.若△P1P3P7,四边形P3P4P6P7的周长分别为a,b,则下列说法中正确的是( )
A. a<b B. a=b C. a>b D. a,b大小无法比较
10 如图,在平面直角坐标系中,正六边形OABCDE的边长是4,则它的内切圆圆心M的坐标是 .
11 如图,在正六边形ABCDEF中,AB=6,点M在边AF上,且AM=2.若经过点M的直线l将正六边形的面积平分,则直线l被正六边形所截的线段长是 W.
12 (1) 如图1,△ABC是⊙O的内接正三角形,P为弧BC上一动点,请探究PA,PB,PC三者之间有何数量关系,并给予证明;
(2) 如图2,四边形ABCD是⊙O的内接正方形,P为弧BC上一动点,请探究PA,PB,PC三者之间有何数量关系,并给予证明;
(3) 如图3,六边形ABCDEF是⊙O的内接正六边形,P为弧BC上一动点,请探究PA,PB,PC三者之间有何数量关系,直接写出结论不需证明.
图1 图2 图3
2.6 正多边形与圆
第1课时 正多边形的有关概念及计算
1. D 2. B 3. 12 4. 10 5. 6. 30
7. 解:如图,连接OB,OC,OD.
因为等边三角形ABC内接于⊙O,BD为内接正十二边形的一条边,
所以∠BOC=×360°=120°,∠BOD=×360°=30°,
所以∠COD=∠BOC-∠BOD=90°.
因为OC=OD,所以△OCD是等腰直角三角形,
所以OC=OD=CD=×5=5(cm),
即⊙O的半径为5 cm.
8. C 9. 60° 10. 12 11. 2
12. 解:连接AC.
因为⊙O的面积为2π,所以⊙O的半径为,
则BD=2=AC,
由正方形的性质知,C是点A关于BD的对称点,
过点C作CA′∥BD,且使CA′=1,
连接AA′交BD于点N,取NM=1,
连接AM,CM,则M,N即为所求点.
因为A′C∥MN,且A′C=MN,
所以四边形MCA′N为平行四边形,
所以A′N=CM=AM,
所以△AMN的周长=AM+AN+MN=AA′+1最小.
因为A′A==3,
所以△AMN周长的最小值为3+1=4.
13. (1) 证明:因为六边形ABCDEF是正六边形,
所以AB=BC=CD=DE=EF=FA,∠A=∠ABC=∠C=∠D=∠DEF=∠F.
因为点P,Q同时分别从A,D两点出发,以1 cm/s的速度沿AF,DC向终点F,C运动,
所以AP=DQ=t,PF=QC=6-t.
在△ABP和△DEQ中,
所以△ABP≌△DEQ(SAS),
所以BP=EQ,同理可证PE=QB,
所以四边形PBQE为平行四边形.
(2) 解:连接BE,OA.
因为∠AOB==60°,OA=OB,
所以△AOB是等边三角形,
所以AB=OA=6 cm,BE=2OB=12 cm.
当t=0时,点P与点A重合,点Q与点D重合,四边形PBQE即为四边形ABDE,如图1,则∠EAF=∠AEF=30°,
所以∠BAE=120°-30°=90°,
所以四边形ABDE是矩形,即四边形PBQE是矩形.
又AE==6(cm),
所以S矩形PBQE=S矩形ABDE=AB·AE=6×6=36(cm2);
当t=6时,点P与点F重合,点Q与点C重合,四边形PBQE即为四边形FBCE,如图2,
同理可知∠BFE=90°,此时四边形PBQE是矩形.
综上,当t=0或t=6时,四边形PBQE是矩形,且矩形PBQE的面积为36 cm2.
因为正六边形ABCDEF的面积=6S△AOB=6×S矩形ABDE=6××36=54(cm2),
所以当四边形PBQE为矩形时,矩形PBQE的面积与正六边形ABCDEF的面积之比为2∶3.
图1 图2
第2课时 正多边形的画法及应用
1. C 2. A 3. C 4. 36° 5. 54°
6. 如图:
7. 解:(1) 因为AE为⊙O的直径,
所以∠AGE=90°.
因为=,
所以AG=EG,
所以∠GAE=∠AEG=45°,
所以AG=EG=10.
(2) 因为ME为⊙O的切线,
所以∠AEM=90°,
由(1)知,∠GAE=45°,
所以ME=AE=20.
8. B 9. A 10. (2,2) 11. 4
12. 解:(1) 如图1,延长BP至点E,使PE=PC,连接CE.
因为A,B,P,C四点共圆,
所以∠BAC+∠BPC=180°.
因为∠BPC+∠EPC=180°,
所以∠BAC=∠CPE=60°.又PE=PC,
所以△PCE是等边三角形,
所以CE=PC,∠E=60°.
又因为∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
所以∠BCE=∠ACP.
因为△ABC,△ECP为等边三角形,
所以CE=PC,AC=BC.
在△BEC和△APC中,,
所以△BEC≌△APC(SAS),
所以PA=EB=PB+PC.
(2) 如图2,过点B作BE⊥PB交PA于点E.
因为∠1+∠2=∠2+∠3=90°,
所以∠1=∠3.
易得∠APB=45°,
所以BP=BE,
所以PE=PB.
在△ABE和△CBP中,
所以△ABE≌△CBP(SAS),
所以PC=AE,
所以PA=AE+PE=PC+PB.
(3) PA=PC+PB.证明如下:
如图3,过点B作BM⊥AP于点M,在AP上截取AQ=PC,连接BQ.
因为∠BAP=∠BCP,AB=BC,
在△ABQ和△CBP中,,
所以△ABQ≌△CBP(SAS),
所以BQ=BP,
所以MP=QM.
在Rt△PBM中,又因为∠APB=30°,所以BM=PB,
所以PM==PB,
所以PQ=PB,
所以PA=PQ+AQ=PC+PB.
图1 图2 图3
第1课时 正多边形的有关概念及计算
1. 各边相等、各角也相等的多边形叫做正多边形.
2. 一般地,只要用量角器把一个圆n(n≥3)等分,依次连接各等分点就能得到这个圆的内接正n边形,这个圆是这个正n边形的外接圆.正多边形的外接圆的圆心叫做正多边形的中心,外接圆的半径叫做正多边形的半径.
建议用时:20分钟
1 (2024济宁)如图,边长为2的正六边形ABCDEF内接于⊙O,则它的内切圆半径为( )
A. 1 B. 2 C. D.
(第1题) (第2题) (第4题) (第5题) (第6题)
2 (2024青岛)为筹备运动会,小松制作了如图所示的宣传牌,在正五边形ABCDE和正方形CDFG中,CF,DG的延长线分别交AE,AB于点M,N,则∠FME的度数是( )
A. 90° B. 99° C. 108° D. 135°
3 (2024南通崇川期中)若正多边形的中心角为30°,则该正多边形的边数为 .
4 (2024镇江)如图,AB是⊙O的内接正n边形的一边,点C在⊙O上,∠ACB=18°,则n= .
5 (2024盐城盐都月考)如图,边长为2的正方形内接于⊙M,则⊙M的半径是 .
6 (2024启东期中)如图,将⊙O的圆周12等分,圆内接矩形ABCD的面积为20,则圆内接正六边形的面积为 .
7 如图,等边三角形ABC内接于⊙O,BD为⊙O内接正十二边形的一条边,CD=5 cm,求⊙O的半径.
建议用时:25+5分钟
8 (2024镇江句容期中)如图,在一个边长为m的正六边形纸板中截去一个边长为m的等边三角形后,余下部分的面积与所截去的等边三角形的面积之比为( )
A. 3∶1 B. 4∶1 C. 5∶1 D. 6∶1
(第8题) (第9题) (第10题) (第11题)
9 (2024南京玄武一模)如图,在正六边形ABCDEF中,经过点E,F的⊙O与边AB,CD分别相切于点G,H,与边DE交于点M,连接GM,FH交于点N,则∠GNF的度数为 .
10 如图,AB,AC分别为⊙O的内接正方形、内接正三角形的边,BC是圆内接正n边形的一边,则n的值为 .
11 如图,六边形ABCDEF是⊙O的内接正六边形,设正六边形ABCDEF的面积为S1,△ACE的面积为S2,则= .
12 如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2π,MN=1,求△AMN周长的最小值.
13 如图,中心为O的正六边形ABCDEF的半径为6 cm,点P,Q同时分别从A,D两点出发,以1 cm/s的速度沿AF,DC向终点F,C运动,连接PB,PE,QB,QE,设运动时间为t s.
(1) 求证:四边形PBQE为平行四边形;
(2) 当四边形PBQE为矩形时,求矩形PBQE的面积与正六边形ABCDEF的面积之比.
第2课时 正多边形的画法及应用
1. 正多边形都是轴对称图形,一个正n边形共有n条对称轴,每条对称轴都经过正n边形的中心.一个正多边形,如果有偶数条边,那么它既是轴对称图形,又是中心对称图形,对称中心就是这个正多边形的中心.
2. 利用直尺和圆规可以画出圆的内接正多边形.依次连接互相垂直的直径端点所得的四边形是圆的内接正方形;以圆的半径为半径,在圆周上依次截取可得6个等分点,并顺次连接这些等分点所得的多边形是圆的内接正六边形.
建议用时:20分钟
1 下列说法中,错误的是( )
A. 正多边形的每个内角都相等 B. 正多边形都是轴对称图形
C. 正多边形都是中心对称图形 D. 正多边形的中心到各边的距离相等
2 如图所示的向日葵图案是用等分圆周画出的,则⊙O的半径与半圆P半径的比为( )
A. 2∶1 B. 4∶1 C. 3∶1 D. 5∶3
(第2题) (第3题) (第4题) (第5题)
3 (2024盐城期中)正六边形蜂巢的建筑结构密合度最高、用材最少、空间最大、也最为坚固.如图,某蜂巢的房孔是边长为6的正六边形ABCDEF,点O是正六边形的中心,则BF的长为( )
A. 12 B. 6 C. 6 D. 12
4 如图,在正五边形ABCDE中,经过C,D两点的⊙O与AB,AE分别相切于点M,N,连接CM,CN,则∠MCN= .
5 如图,在正十边形A1A2A3A4A5A6A7A8A9A10中,连接A1A4,A1A7,则∠A4A1A7= .
6 在如图所示的三个圆中,用尺规作图作出正方形ABCD、正六边形ABCDEF和正三角形ABC.(要求:保留作图痕迹,不写作法)
7 (2024扬州广陵期中)司南是我国古代辨别方向用的一种仪器.其早在战国时期就已被发明,是现在所用指南针的始祖.如图,司南中心为一圆形,圆心为点O,直径为20,根据八个方位将圆形八等分(图2中点A~H),过点E作⊙O的切线与AG的延长线交于点M,连接EG.
(1) 求AG的长;
(2) 求ME的长.
图1 图2
建议用时:25+5分钟
8 (2024盐城射阳月考)刘徽在《九章算术注》中首创“割圆术”,利用圆的内接正多边形来确定圆周率,开创了中国数学发展史上圆周率研究的新纪元.某同学在学习“割圆术”的过程中,作了一个如图所示的圆内接正十二边形.若⊙O的半径为2,则这个圆内接正十二边形的面积为( )
A. 3 B. 12 C. 4π D. 12π
(第8题) (第9题) (第10题) (第11题)
9 如图,P1~P8是⊙O的八等分点.若△P1P3P7,四边形P3P4P6P7的周长分别为a,b,则下列说法中正确的是( )
A. a<b B. a=b C. a>b D. a,b大小无法比较
10 如图,在平面直角坐标系中,正六边形OABCDE的边长是4,则它的内切圆圆心M的坐标是 .
11 如图,在正六边形ABCDEF中,AB=6,点M在边AF上,且AM=2.若经过点M的直线l将正六边形的面积平分,则直线l被正六边形所截的线段长是 W.
12 (1) 如图1,△ABC是⊙O的内接正三角形,P为弧BC上一动点,请探究PA,PB,PC三者之间有何数量关系,并给予证明;
(2) 如图2,四边形ABCD是⊙O的内接正方形,P为弧BC上一动点,请探究PA,PB,PC三者之间有何数量关系,并给予证明;
(3) 如图3,六边形ABCDEF是⊙O的内接正六边形,P为弧BC上一动点,请探究PA,PB,PC三者之间有何数量关系,直接写出结论不需证明.
图1 图2 图3
2.6 正多边形与圆
第1课时 正多边形的有关概念及计算
1. D 2. B 3. 12 4. 10 5. 6. 30
7. 解:如图,连接OB,OC,OD.
因为等边三角形ABC内接于⊙O,BD为内接正十二边形的一条边,
所以∠BOC=×360°=120°,∠BOD=×360°=30°,
所以∠COD=∠BOC-∠BOD=90°.
因为OC=OD,所以△OCD是等腰直角三角形,
所以OC=OD=CD=×5=5(cm),
即⊙O的半径为5 cm.
8. C 9. 60° 10. 12 11. 2
12. 解:连接AC.
因为⊙O的面积为2π,所以⊙O的半径为,
则BD=2=AC,
由正方形的性质知,C是点A关于BD的对称点,
过点C作CA′∥BD,且使CA′=1,
连接AA′交BD于点N,取NM=1,
连接AM,CM,则M,N即为所求点.
因为A′C∥MN,且A′C=MN,
所以四边形MCA′N为平行四边形,
所以A′N=CM=AM,
所以△AMN的周长=AM+AN+MN=AA′+1最小.
因为A′A==3,
所以△AMN周长的最小值为3+1=4.
13. (1) 证明:因为六边形ABCDEF是正六边形,
所以AB=BC=CD=DE=EF=FA,∠A=∠ABC=∠C=∠D=∠DEF=∠F.
因为点P,Q同时分别从A,D两点出发,以1 cm/s的速度沿AF,DC向终点F,C运动,
所以AP=DQ=t,PF=QC=6-t.
在△ABP和△DEQ中,
所以△ABP≌△DEQ(SAS),
所以BP=EQ,同理可证PE=QB,
所以四边形PBQE为平行四边形.
(2) 解:连接BE,OA.
因为∠AOB==60°,OA=OB,
所以△AOB是等边三角形,
所以AB=OA=6 cm,BE=2OB=12 cm.
当t=0时,点P与点A重合,点Q与点D重合,四边形PBQE即为四边形ABDE,如图1,则∠EAF=∠AEF=30°,
所以∠BAE=120°-30°=90°,
所以四边形ABDE是矩形,即四边形PBQE是矩形.
又AE==6(cm),
所以S矩形PBQE=S矩形ABDE=AB·AE=6×6=36(cm2);
当t=6时,点P与点F重合,点Q与点C重合,四边形PBQE即为四边形FBCE,如图2,
同理可知∠BFE=90°,此时四边形PBQE是矩形.
综上,当t=0或t=6时,四边形PBQE是矩形,且矩形PBQE的面积为36 cm2.
因为正六边形ABCDEF的面积=6S△AOB=6×S矩形ABDE=6××36=54(cm2),
所以当四边形PBQE为矩形时,矩形PBQE的面积与正六边形ABCDEF的面积之比为2∶3.
图1 图2
第2课时 正多边形的画法及应用
1. C 2. A 3. C 4. 36° 5. 54°
6. 如图:
7. 解:(1) 因为AE为⊙O的直径,
所以∠AGE=90°.
因为=,
所以AG=EG,
所以∠GAE=∠AEG=45°,
所以AG=EG=10.
(2) 因为ME为⊙O的切线,
所以∠AEM=90°,
由(1)知,∠GAE=45°,
所以ME=AE=20.
8. B 9. A 10. (2,2) 11. 4
12. 解:(1) 如图1,延长BP至点E,使PE=PC,连接CE.
因为A,B,P,C四点共圆,
所以∠BAC+∠BPC=180°.
因为∠BPC+∠EPC=180°,
所以∠BAC=∠CPE=60°.又PE=PC,
所以△PCE是等边三角形,
所以CE=PC,∠E=60°.
又因为∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
所以∠BCE=∠ACP.
因为△ABC,△ECP为等边三角形,
所以CE=PC,AC=BC.
在△BEC和△APC中,,
所以△BEC≌△APC(SAS),
所以PA=EB=PB+PC.
(2) 如图2,过点B作BE⊥PB交PA于点E.
因为∠1+∠2=∠2+∠3=90°,
所以∠1=∠3.
易得∠APB=45°,
所以BP=BE,
所以PE=PB.
在△ABE和△CBP中,
所以△ABE≌△CBP(SAS),
所以PC=AE,
所以PA=AE+PE=PC+PB.
(3) PA=PC+PB.证明如下:
如图3,过点B作BM⊥AP于点M,在AP上截取AQ=PC,连接BQ.
因为∠BAP=∠BCP,AB=BC,
在△ABQ和△CBP中,,
所以△ABQ≌△CBP(SAS),
所以BQ=BP,
所以MP=QM.
在Rt△PBM中,又因为∠APB=30°,所以BM=PB,
所以PM==PB,
所以PQ=PB,
所以PA=PQ+AQ=PC+PB.
图1 图2 图3
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
