4.2 等可能条件下的概率(一) 同步练(含答案) 2025-2026学年数学苏科版九年级上册
文档属性
| 名称 | 4.2 等可能条件下的概率(一) 同步练(含答案) 2025-2026学年数学苏科版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 212.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 00:00:00 | ||
图片预览




文档简介
4.2 等可能条件下的概率(一)
第1课时 用枚举法求简单随机事件的概率
一般地,如果一个试验有n个等可能的结果,当其中的m个结果之一出现时,事件A发生,那么事件A发生的概率为P(A)=,其中m表示事件A发生可能出现的结果数,n表示一次试验所有等可能出现的结果数.
建议用时:20分钟
1 (2024广西)一只不透明袋子中装有白球2个,红球1个,这些球除了颜色外无其他差别.从袋子中随机取出1个球,取出白球的概率是( )
A. 1 B. C. D.
2 (2024广东)长江是中华民族的母亲河,长江流域孕育出藏羌文化、巴蜀文化、荆楚文化、吴越文化等区域文化.若从上述四种区域文化中随机选一种文化开展专题学习,则选中“巴蜀文化”的概率是( )
A. B. C. D.
3 (2024泸州)在一个不透明的盒子中装有6个白球,若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球是白球的概率是,则黄球的个数为 .
4 (2024浙江)有8张卡片,上面分别写着数字1,2,3,4,5,6,7,8.从中随机抽取1张,该卡片上的数是4的整数倍的概率是 .
5 (2024雅安)将-2,,π,0,,3.14这6个数字分别写在6张同样的卡片上,从中随机抽取1张,卡片上的数为有理数的概率是 .
6 (2024湖南)有四枚材质、大小、背面图案完全相同的中国象棋棋子“”“”“”“”,将它们背面朝上任意放置,从中随机翻开一枚,恰好翻到棋子“”的概率是 .
7 一副扑克牌(无大王、小王),从中任意取出一张,共有52种等可能的结果.
(1) 列出抽到K的所有可能的结果;
(2) 求抽到红桃K的概率;
(3) 求抽到K的概率;
(4) 求抽到红桃的概率;
(5) 若抽到红桃你赢,抽不到红桃老师赢,你认为这个游戏公平吗?为什么?
建议用时:25+5分钟
8 抛掷一枚质地均匀的1元硬币10次,有9次正面朝上,1次反面朝上.若第11次抛掷该硬币,则正面朝上的概率是( )
A. B. C. D. 无法确定
9 如图,将一个棱长为3的正方体表面涂上颜色,再把它分割成棱长为1的小正方体,将它们全部放入一个不透明盒子中摇匀,随机取出一个小正方体,只有一个面被涂色的概率为( )
A. B. C. D.
(第9题) (第10题) (第11题)
10 如图,电路图上有A,B,C三个开关和一个小灯泡,闭合开关C或者同时闭合开关A,B,都可使小灯泡发光,现在任意闭合其中一个开关,则小灯泡发光的概率等于 .
11 如图,点A,B在由边长为1的小正方形组成的网格的格点上,在网格格点上除点A,B外任取一点C,则使△ABC的面积为1的概率是 .
12 围棋盒中有x颗白色棋子,y颗黑色棋子,从盒中随机地取出一颗棋子,若它是白色棋子的概率是.
(1) 写出y与x的函数表达式;
(2) 第一次取出的棋子放回盒中,再往盒中放入6颗白色棋子,若随机取出一颗白色棋子的概率为,分别求出x和y的值.
13 如图,现有一个转盘被分成6等份,分别标有2,3,4,5,6,7这六个数字.转动转盘,当转盘停止时,指针指向的数字即为转出的数字.
(1) 转动转盘,转出的数字大于3的概率是 ;
(2) 现有两张分别写有3,4的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度,求这三条线段能构成直角三角形的概率.
第2课时 用树状图法求等可能条件下的概率
通过画树状图可以帮助我们不重复、不遗漏地列出随机试验的所有可能的结果,然后找出符合条件的结果,用概率公式求出随机事件的概率.
建议用时:20分钟
1 某校在劳动课上,设置了植树、种花、除草三个劳动项目.九年级一班和九年级二班都通过抽签的方式从这三个项目中随机抽取一个项目,则这两个班级恰好都抽到种花的概率是( )
A. B. C. D.
2 (2024齐齐哈尔)六月份,在“阳光大课间”活动中,某校设计了“篮球、足球、排球、羽毛球”四种球类运动项目,且每名学生在一个大课间只能选择参加一种运动项目,则甲、乙两名学生在一个大课间参加同种球类运动项目的概率是( )
A. B. C. D.
3 (2024济南)3月14日是国际数学节.某学校在今年国际数学节策划了“竞速华容道”“玩转幻方”和“巧解鲁班锁”三个挑战活动,若小红和小丽每人随机选择参加其中一个活动,则她们恰好选到同一个活动的概率是( )
A. B. C. D.
4 (2024黑龙江)七年级一班要从2名男生和3名女生中选择两名学生参加朗诵比赛,恰好选择1名男生和1名女生的概率是 .
5 (2024潍坊)小莹在做手抄报时,用到了红色、黄色、蓝色三支彩笔,这三支彩笔的笔帽和笔芯颜色分别一致.完成手抄报后,她随机地将三个笔帽分别盖在三支彩笔上,每个笔帽和笔芯的颜色都不匹配的概率是 .
6 (2024德州)衣橱里挂着3套不同颜色的服装,同一套服装的上衣与裤子的颜色相同,若从衣橱里各任取一件上衣和一条裤子,则它们取自同一套的概率是 .
7 (2024镇江)3张相同的卡片上分别写有中国二十四节气中的“小满”“芒种”“夏至”的字样,将卡片的背面朝上.
(1) 洗匀后,从中任意抽取1张卡片,抽到写有“小满”的卡片的概率等于 ;
(2) 洗匀后,从中任意抽取2张卡片,用画树状图或列表的方法,求抽到一张写有“芒种”,一张写有“夏至”的卡片的概率.
建议用时:25+5分钟
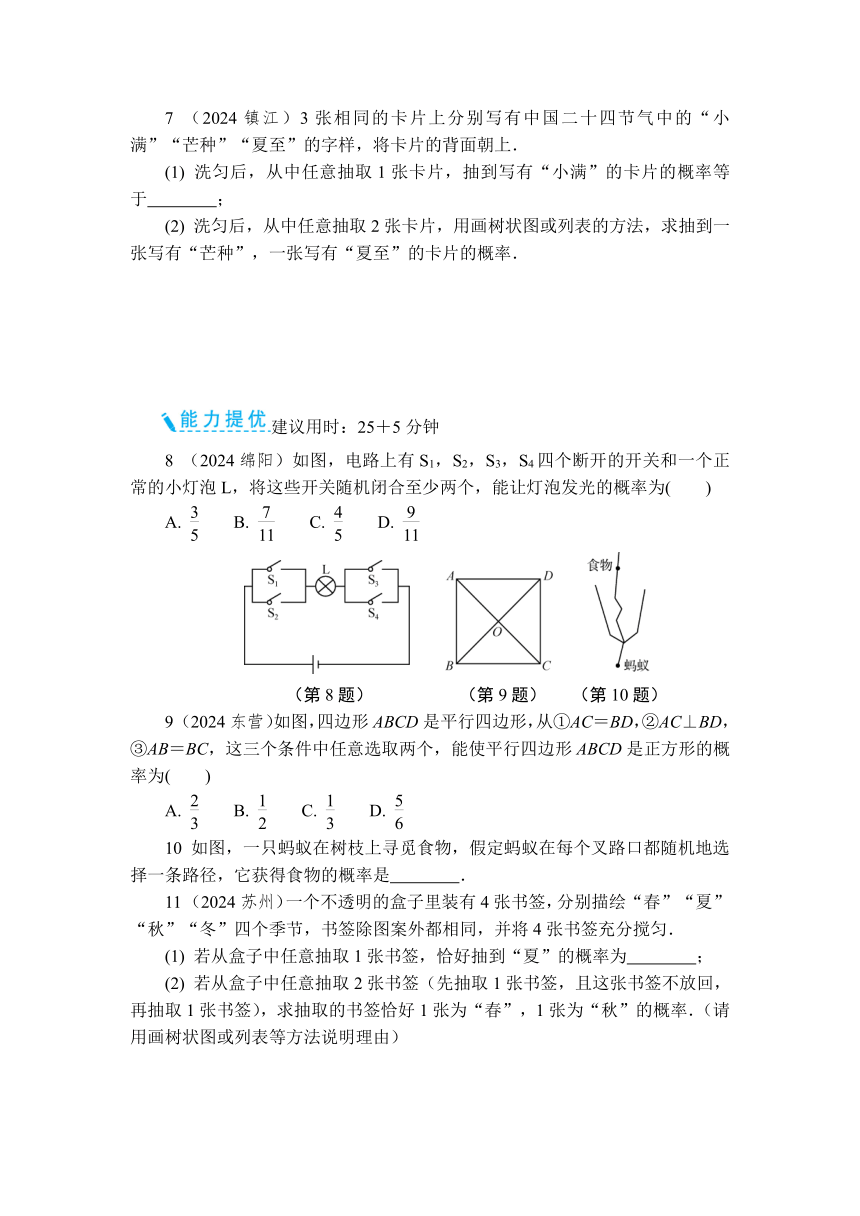
8 (2024绵阳)如图,电路上有S1,S2,S3,S4四个断开的开关和一个正常的小灯泡L,将这些开关随机闭合至少两个,能让灯泡发光的概率为( )
A. B. C. D.
(第8题) (第9题) (第10题)
9 (2024东营)如图,四边形ABCD是平行四边形,从①AC=BD,②AC⊥BD,③AB=BC,这三个条件中任意选取两个,能使平行四边形ABCD是正方形的概率为( )
A. B. C. D.
10 如图,一只蚂蚁在树枝上寻觅食物,假定蚂蚁在每个叉路口都随机地选择一条路径,它获得食物的概率是 .
11 (2024苏州)一个不透明的盒子里装有4张书签,分别描绘“春”“夏”
“秋”“冬”四个季节,书签除图案外都相同,并将4张书签充分搅匀.
(1) 若从盒子中任意抽取1张书签,恰好抽到“夏”的概率为 ;
(2) 若从盒子中任意抽取2张书签(先抽取1张书签,且这张书签不放回,再抽取1张书签),求抽取的书签恰好1张为“春”,1张为“秋”的概率.(请用画树状图或列表等方法说明理由)
12 甲、乙、丙、丁四个人做“击鼓传花”的游戏,游戏规则是:第一次由甲将花随机传给乙、丙、丁三人中的某一人,以后的每一次传花都是由接到花的人随机传给其他三人中的某一人.
(1) 甲第一次传花时,恰好传给乙的概率是 ;
(2) 请用画树状图法,求经过两次传花,花恰好回到甲手中的概率;
(3) 经过三次传花,花落在丙手上的概率记作P1,落在丁手上的概率记作P2,则P1 P2.(填“>”“<”或“=”)
第3课时 用列表法求等可能条件下的概率
一次试验可能出现的结果数目较多时,为书写方便,通常采用列表法列出随机事件在一次试验中所有可能的结果,然后找出符合条件的结果,用概率公式求出随机事件的概率.另外,列表时可用符号表示复杂的名称.
建议用时:20分钟
1 (2024北京)一只不透明袋子中仅有红、黄色小球各一个,两个小球除颜色外无其他差别.从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,则两次摸出的都是红球的概率是( )
A. B. C. D.
2 哥德巴赫提出“每个大于2的偶数都可以表示为两个质数之和”的猜想,我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.在质数2,3,5中,随机选取两个不同的数,其和是偶数的概率是( )
A. B. C. D.
3 学校招募运动会广播员,从两名男生和两名女生共四名候选人中随机选取两人,则两人恰好是一男一女的概率为 .
4 一个盒子里放有草莓味、柠檬味的两种糖各1块,另一个盒子里放有草莓味、柠檬味、葡萄味的三种糖各1块,糖的外形相同.小亮从两个盒子中各随机取出一块糖,则两块糖是不同味的概率是 .
5 为了有效保护环境,某居委会倡议居民将生活垃圾进行可回收的、不可回收的和有害的分类投放.一天,小林把垃圾分装在三个袋中,则他任意投放垃圾,把三个袋子都放错位的概率是 .
6 (2024泰安)某学校在4月23日世界读书日举行“书香校园,全员阅读”活动.小明和小颖去学校图书室借阅书籍,小明准备从《西游记》《骆驼祥子》《水浒传》中随机选择一本,小颖准备从《西游记》《骆驼祥子》《朝花夕拾》中随机选择一本,小明和小颖恰好选中书名相同的书的概率是 .
7 (2024宿迁)某校组织七年级学生开展以“讲好红色故事,传承红色基因”为主题的研学活动,策划了四条研学线路供学生选择:A彭雪枫纪念馆,B淮海军政大礼堂,C爱园烈士陵园,D大王庄党性教育基地,每名学生只能任意选择一条线路.
(1) 小刚选择线路A的概率为 ;
(2) 请用画树状图或列表的方法,求小刚和小红选择同一线路的概率.
建议用时:25+5分钟
8 如图,在三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以围成一个矩形,从这些矩形中任选一个,则所选矩形含点A的概率是( )
A. B. C. D.
9 有三张背面完全相同的卡片,正面上分别标有数字1,-1,2.把这三张卡片背面朝上,随机抽取一张,记下数字为a;不放回,在剩余的卡片中再随机抽取一张,记下数字为b,则方程x2+ax+b=0有解的概率是 .
10 (2024宿迁月考)四张相同的卡片上分别写有数字-1,-5,2,4,将卡片的背面向上洗匀后从中任意抽1张,并将卡片上数字记为k,再从余下的卡片中任意抽1张,并将卡片上数字记为b,则一次函数y=kx+b的图像经过第二、三、四象限的概率为 .
11 如图,A,B两个带指针的转盘分别被分成三个面积相等的扇形,转盘A上的数字分别是-6,-1,5,转盘B上的数字分别是6,-7,4(两个转盘除表面数字不同外,其他完全相同).小聪和小明同时转动A,B两个转盘,使之旋转(规定:若指针恰好停留在分界线上,则重新转一次).
(1) 转动转盘,转盘A指针指向正数的概率是 ;
(2) 若同时转动两个转盘,转盘A指针所指的数字记为a,转盘B指针所指的数字记为b,若a+b>0,则小聪获胜;若a+b<0,则小明获胜.请用列表法说明这个游戏是否公平.
12 有甲、乙两个不透明的布袋,甲袋中装有三个完全相同的小球,分别标有数字0,1,2;乙袋中装有三个完全相同的小球,分别标有数字-1,-2,0.现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M的坐标为(x,y).
(1) 用列表法列举点M所有可能的坐标;
(2) 求点M(x,y)在函数y=-x+1的图像上的概率;
(3) 在平面直角坐标系xOy中,⊙O的半径是2,求过点M(x,y)能作⊙O的切线的概率.
4.2 等可能条件下的概率(一)
第1课时 用枚举法求简单随机事件的概率
1. D 2. A 3. 3 4. 5. 6.
7. 解:(1) 抽到K的所有可能的结果为红桃K,黑桃K,方块K,梅花K.
(2) P(抽到红桃K)=.
(3) P(抽到K)=.
(4) P(抽到红桃)=.
(5) 因为P(抽到红桃)=,P(抽不到红桃)=,
所以游戏不公平.
8. B 9. B 10. 11.
12. 解:(1) 因为随机地取出一颗棋子是白色棋子的概率是,
所以随机地取出一颗棋子是黑色棋子的概率是,
所以黑色棋子与白色棋子之比为3∶5,
所以y=x.
(2) 由题意,得=,解得x=30,
经检验x=30是原方程的解,
所以y=×30=18.
13. 解:(1)
(2) 因为转盘被分成6等份,转到每个数字的可能性相等,共6种可能结果,能构成直角三角形的结果只有1种,
即转到5,所以P(构成直角三角形)=.
第2课时 用树状图法求等可能条件下的概率
1. D 2. C 3. C 4. 5. 6.
7. 解:(1)
(2) 把写有中国二十四节气中的“小满”“芒种”“夏至”3张卡片分别记为A,B,C,
画树状图如下:
共有6种等可能的结果,其中抽到一张写有“芒种”,一张写有“夏至”的卡片的结果有2种,
所以抽到一张写有“芒种”,一张写有“夏至”的卡片的概率为=.
8. D 9. A 10.
11. 解:(1)
(2) 画树状图如下:
共有12种等可能的结果,其中抽取的书签恰好1张为“春”,1张为“秋”的结果有2种,
所以抽取的书签恰好1张为“春”,1张为“秋”的概率为=.
12. 解:(1)
(2) 根据题意画树状图如下:
由树状图可知,共有9种等可能的结果,其中符合要求的结果有3种,所以P=.
(3) =
第3课时 用列表法求等可能条件下的概率
1. A 2. B 3. 4. 5. 6.
7. 解:(1)
(2) 列表如下:
小刚 小红
A B C D
A (A,A) (A,B) (A,C) (A,D)
B (B,A) (B,B) (B,C) (B,D)
C (C,A) (C,B) (C,C) (C,D)
D (D,A) (D,B) (D,C) (D,D)
共有16种等可能的结果,其中小刚和小红选择同一线路的结果有4种,
所以小刚和小红选择同一线路的概率为=.
8. D 9. 10.
11. 解:(1)
(2) 列表如下:
b a
-6 -1 5
6 0 5 11
-7 -13 -8 -2
4 -2 3 9
由表可知一共有9种等可能的结果,其中a+b>0有4种可能的结果,a+b<0有4种等可能的结果,
所以P(小聪获胜)=,P(小明获胜)=,
因为P(小聪获胜)=P(小明获胜),所以这个游戏公平.
12. 解:(1) 列表如下:
甲 乙
-1 -2 0
0 (0,-1) (0,-2) (0,0)
1 (1,-1) (1,-2) (1,0)
2 (2,-1) (2,-2) (2,0)
由表格可知,点M(x,y)的坐标共有9种等可能的结果.
(2) 在函数y=-x+1的图像上的点M为(1,0),(2,-1),所以所求概率P=.
(3) 点M在⊙O上或⊙O外的点为(0,-2),(1,-2),(2,-1),(2,-2),(2,0),
所以过点M能作⊙O的切线的概率P=.
第1课时 用枚举法求简单随机事件的概率
一般地,如果一个试验有n个等可能的结果,当其中的m个结果之一出现时,事件A发生,那么事件A发生的概率为P(A)=,其中m表示事件A发生可能出现的结果数,n表示一次试验所有等可能出现的结果数.
建议用时:20分钟
1 (2024广西)一只不透明袋子中装有白球2个,红球1个,这些球除了颜色外无其他差别.从袋子中随机取出1个球,取出白球的概率是( )
A. 1 B. C. D.
2 (2024广东)长江是中华民族的母亲河,长江流域孕育出藏羌文化、巴蜀文化、荆楚文化、吴越文化等区域文化.若从上述四种区域文化中随机选一种文化开展专题学习,则选中“巴蜀文化”的概率是( )
A. B. C. D.
3 (2024泸州)在一个不透明的盒子中装有6个白球,若干个黄球,它们除颜色不同外,其余均相同.若从中随机摸出一个球是白球的概率是,则黄球的个数为 .
4 (2024浙江)有8张卡片,上面分别写着数字1,2,3,4,5,6,7,8.从中随机抽取1张,该卡片上的数是4的整数倍的概率是 .
5 (2024雅安)将-2,,π,0,,3.14这6个数字分别写在6张同样的卡片上,从中随机抽取1张,卡片上的数为有理数的概率是 .
6 (2024湖南)有四枚材质、大小、背面图案完全相同的中国象棋棋子“”“”“”“”,将它们背面朝上任意放置,从中随机翻开一枚,恰好翻到棋子“”的概率是 .
7 一副扑克牌(无大王、小王),从中任意取出一张,共有52种等可能的结果.
(1) 列出抽到K的所有可能的结果;
(2) 求抽到红桃K的概率;
(3) 求抽到K的概率;
(4) 求抽到红桃的概率;
(5) 若抽到红桃你赢,抽不到红桃老师赢,你认为这个游戏公平吗?为什么?
建议用时:25+5分钟
8 抛掷一枚质地均匀的1元硬币10次,有9次正面朝上,1次反面朝上.若第11次抛掷该硬币,则正面朝上的概率是( )
A. B. C. D. 无法确定
9 如图,将一个棱长为3的正方体表面涂上颜色,再把它分割成棱长为1的小正方体,将它们全部放入一个不透明盒子中摇匀,随机取出一个小正方体,只有一个面被涂色的概率为( )
A. B. C. D.
(第9题) (第10题) (第11题)
10 如图,电路图上有A,B,C三个开关和一个小灯泡,闭合开关C或者同时闭合开关A,B,都可使小灯泡发光,现在任意闭合其中一个开关,则小灯泡发光的概率等于 .
11 如图,点A,B在由边长为1的小正方形组成的网格的格点上,在网格格点上除点A,B外任取一点C,则使△ABC的面积为1的概率是 .
12 围棋盒中有x颗白色棋子,y颗黑色棋子,从盒中随机地取出一颗棋子,若它是白色棋子的概率是.
(1) 写出y与x的函数表达式;
(2) 第一次取出的棋子放回盒中,再往盒中放入6颗白色棋子,若随机取出一颗白色棋子的概率为,分别求出x和y的值.
13 如图,现有一个转盘被分成6等份,分别标有2,3,4,5,6,7这六个数字.转动转盘,当转盘停止时,指针指向的数字即为转出的数字.
(1) 转动转盘,转出的数字大于3的概率是 ;
(2) 现有两张分别写有3,4的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度,求这三条线段能构成直角三角形的概率.
第2课时 用树状图法求等可能条件下的概率
通过画树状图可以帮助我们不重复、不遗漏地列出随机试验的所有可能的结果,然后找出符合条件的结果,用概率公式求出随机事件的概率.
建议用时:20分钟
1 某校在劳动课上,设置了植树、种花、除草三个劳动项目.九年级一班和九年级二班都通过抽签的方式从这三个项目中随机抽取一个项目,则这两个班级恰好都抽到种花的概率是( )
A. B. C. D.
2 (2024齐齐哈尔)六月份,在“阳光大课间”活动中,某校设计了“篮球、足球、排球、羽毛球”四种球类运动项目,且每名学生在一个大课间只能选择参加一种运动项目,则甲、乙两名学生在一个大课间参加同种球类运动项目的概率是( )
A. B. C. D.
3 (2024济南)3月14日是国际数学节.某学校在今年国际数学节策划了“竞速华容道”“玩转幻方”和“巧解鲁班锁”三个挑战活动,若小红和小丽每人随机选择参加其中一个活动,则她们恰好选到同一个活动的概率是( )
A. B. C. D.
4 (2024黑龙江)七年级一班要从2名男生和3名女生中选择两名学生参加朗诵比赛,恰好选择1名男生和1名女生的概率是 .
5 (2024潍坊)小莹在做手抄报时,用到了红色、黄色、蓝色三支彩笔,这三支彩笔的笔帽和笔芯颜色分别一致.完成手抄报后,她随机地将三个笔帽分别盖在三支彩笔上,每个笔帽和笔芯的颜色都不匹配的概率是 .
6 (2024德州)衣橱里挂着3套不同颜色的服装,同一套服装的上衣与裤子的颜色相同,若从衣橱里各任取一件上衣和一条裤子,则它们取自同一套的概率是 .
7 (2024镇江)3张相同的卡片上分别写有中国二十四节气中的“小满”“芒种”“夏至”的字样,将卡片的背面朝上.
(1) 洗匀后,从中任意抽取1张卡片,抽到写有“小满”的卡片的概率等于 ;
(2) 洗匀后,从中任意抽取2张卡片,用画树状图或列表的方法,求抽到一张写有“芒种”,一张写有“夏至”的卡片的概率.
建议用时:25+5分钟
8 (2024绵阳)如图,电路上有S1,S2,S3,S4四个断开的开关和一个正常的小灯泡L,将这些开关随机闭合至少两个,能让灯泡发光的概率为( )
A. B. C. D.
(第8题) (第9题) (第10题)
9 (2024东营)如图,四边形ABCD是平行四边形,从①AC=BD,②AC⊥BD,③AB=BC,这三个条件中任意选取两个,能使平行四边形ABCD是正方形的概率为( )
A. B. C. D.
10 如图,一只蚂蚁在树枝上寻觅食物,假定蚂蚁在每个叉路口都随机地选择一条路径,它获得食物的概率是 .
11 (2024苏州)一个不透明的盒子里装有4张书签,分别描绘“春”“夏”
“秋”“冬”四个季节,书签除图案外都相同,并将4张书签充分搅匀.
(1) 若从盒子中任意抽取1张书签,恰好抽到“夏”的概率为 ;
(2) 若从盒子中任意抽取2张书签(先抽取1张书签,且这张书签不放回,再抽取1张书签),求抽取的书签恰好1张为“春”,1张为“秋”的概率.(请用画树状图或列表等方法说明理由)
12 甲、乙、丙、丁四个人做“击鼓传花”的游戏,游戏规则是:第一次由甲将花随机传给乙、丙、丁三人中的某一人,以后的每一次传花都是由接到花的人随机传给其他三人中的某一人.
(1) 甲第一次传花时,恰好传给乙的概率是 ;
(2) 请用画树状图法,求经过两次传花,花恰好回到甲手中的概率;
(3) 经过三次传花,花落在丙手上的概率记作P1,落在丁手上的概率记作P2,则P1 P2.(填“>”“<”或“=”)
第3课时 用列表法求等可能条件下的概率
一次试验可能出现的结果数目较多时,为书写方便,通常采用列表法列出随机事件在一次试验中所有可能的结果,然后找出符合条件的结果,用概率公式求出随机事件的概率.另外,列表时可用符号表示复杂的名称.
建议用时:20分钟
1 (2024北京)一只不透明袋子中仅有红、黄色小球各一个,两个小球除颜色外无其他差别.从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,则两次摸出的都是红球的概率是( )
A. B. C. D.
2 哥德巴赫提出“每个大于2的偶数都可以表示为两个质数之和”的猜想,我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.在质数2,3,5中,随机选取两个不同的数,其和是偶数的概率是( )
A. B. C. D.
3 学校招募运动会广播员,从两名男生和两名女生共四名候选人中随机选取两人,则两人恰好是一男一女的概率为 .
4 一个盒子里放有草莓味、柠檬味的两种糖各1块,另一个盒子里放有草莓味、柠檬味、葡萄味的三种糖各1块,糖的外形相同.小亮从两个盒子中各随机取出一块糖,则两块糖是不同味的概率是 .
5 为了有效保护环境,某居委会倡议居民将生活垃圾进行可回收的、不可回收的和有害的分类投放.一天,小林把垃圾分装在三个袋中,则他任意投放垃圾,把三个袋子都放错位的概率是 .
6 (2024泰安)某学校在4月23日世界读书日举行“书香校园,全员阅读”活动.小明和小颖去学校图书室借阅书籍,小明准备从《西游记》《骆驼祥子》《水浒传》中随机选择一本,小颖准备从《西游记》《骆驼祥子》《朝花夕拾》中随机选择一本,小明和小颖恰好选中书名相同的书的概率是 .
7 (2024宿迁)某校组织七年级学生开展以“讲好红色故事,传承红色基因”为主题的研学活动,策划了四条研学线路供学生选择:A彭雪枫纪念馆,B淮海军政大礼堂,C爱园烈士陵园,D大王庄党性教育基地,每名学生只能任意选择一条线路.
(1) 小刚选择线路A的概率为 ;
(2) 请用画树状图或列表的方法,求小刚和小红选择同一线路的概率.
建议用时:25+5分钟
8 如图,在三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以围成一个矩形,从这些矩形中任选一个,则所选矩形含点A的概率是( )
A. B. C. D.
9 有三张背面完全相同的卡片,正面上分别标有数字1,-1,2.把这三张卡片背面朝上,随机抽取一张,记下数字为a;不放回,在剩余的卡片中再随机抽取一张,记下数字为b,则方程x2+ax+b=0有解的概率是 .
10 (2024宿迁月考)四张相同的卡片上分别写有数字-1,-5,2,4,将卡片的背面向上洗匀后从中任意抽1张,并将卡片上数字记为k,再从余下的卡片中任意抽1张,并将卡片上数字记为b,则一次函数y=kx+b的图像经过第二、三、四象限的概率为 .
11 如图,A,B两个带指针的转盘分别被分成三个面积相等的扇形,转盘A上的数字分别是-6,-1,5,转盘B上的数字分别是6,-7,4(两个转盘除表面数字不同外,其他完全相同).小聪和小明同时转动A,B两个转盘,使之旋转(规定:若指针恰好停留在分界线上,则重新转一次).
(1) 转动转盘,转盘A指针指向正数的概率是 ;
(2) 若同时转动两个转盘,转盘A指针所指的数字记为a,转盘B指针所指的数字记为b,若a+b>0,则小聪获胜;若a+b<0,则小明获胜.请用列表法说明这个游戏是否公平.
12 有甲、乙两个不透明的布袋,甲袋中装有三个完全相同的小球,分别标有数字0,1,2;乙袋中装有三个完全相同的小球,分别标有数字-1,-2,0.现从甲袋中随机抽取一个小球,记录标有的数字为x,再从乙袋中随机抽取一个小球,记录标有的数字为y,确定点M的坐标为(x,y).
(1) 用列表法列举点M所有可能的坐标;
(2) 求点M(x,y)在函数y=-x+1的图像上的概率;
(3) 在平面直角坐标系xOy中,⊙O的半径是2,求过点M(x,y)能作⊙O的切线的概率.
4.2 等可能条件下的概率(一)
第1课时 用枚举法求简单随机事件的概率
1. D 2. A 3. 3 4. 5. 6.
7. 解:(1) 抽到K的所有可能的结果为红桃K,黑桃K,方块K,梅花K.
(2) P(抽到红桃K)=.
(3) P(抽到K)=.
(4) P(抽到红桃)=.
(5) 因为P(抽到红桃)=,P(抽不到红桃)=,
所以游戏不公平.
8. B 9. B 10. 11.
12. 解:(1) 因为随机地取出一颗棋子是白色棋子的概率是,
所以随机地取出一颗棋子是黑色棋子的概率是,
所以黑色棋子与白色棋子之比为3∶5,
所以y=x.
(2) 由题意,得=,解得x=30,
经检验x=30是原方程的解,
所以y=×30=18.
13. 解:(1)
(2) 因为转盘被分成6等份,转到每个数字的可能性相等,共6种可能结果,能构成直角三角形的结果只有1种,
即转到5,所以P(构成直角三角形)=.
第2课时 用树状图法求等可能条件下的概率
1. D 2. C 3. C 4. 5. 6.
7. 解:(1)
(2) 把写有中国二十四节气中的“小满”“芒种”“夏至”3张卡片分别记为A,B,C,
画树状图如下:
共有6种等可能的结果,其中抽到一张写有“芒种”,一张写有“夏至”的卡片的结果有2种,
所以抽到一张写有“芒种”,一张写有“夏至”的卡片的概率为=.
8. D 9. A 10.
11. 解:(1)
(2) 画树状图如下:
共有12种等可能的结果,其中抽取的书签恰好1张为“春”,1张为“秋”的结果有2种,
所以抽取的书签恰好1张为“春”,1张为“秋”的概率为=.
12. 解:(1)
(2) 根据题意画树状图如下:
由树状图可知,共有9种等可能的结果,其中符合要求的结果有3种,所以P=.
(3) =
第3课时 用列表法求等可能条件下的概率
1. A 2. B 3. 4. 5. 6.
7. 解:(1)
(2) 列表如下:
小刚 小红
A B C D
A (A,A) (A,B) (A,C) (A,D)
B (B,A) (B,B) (B,C) (B,D)
C (C,A) (C,B) (C,C) (C,D)
D (D,A) (D,B) (D,C) (D,D)
共有16种等可能的结果,其中小刚和小红选择同一线路的结果有4种,
所以小刚和小红选择同一线路的概率为=.
8. D 9. 10.
11. 解:(1)
(2) 列表如下:
b a
-6 -1 5
6 0 5 11
-7 -13 -8 -2
4 -2 3 9
由表可知一共有9种等可能的结果,其中a+b>0有4种可能的结果,a+b<0有4种等可能的结果,
所以P(小聪获胜)=,P(小明获胜)=,
因为P(小聪获胜)=P(小明获胜),所以这个游戏公平.
12. 解:(1) 列表如下:
甲 乙
-1 -2 0
0 (0,-1) (0,-2) (0,0)
1 (1,-1) (1,-2) (1,0)
2 (2,-1) (2,-2) (2,0)
由表格可知,点M(x,y)的坐标共有9种等可能的结果.
(2) 在函数y=-x+1的图像上的点M为(1,0),(2,-1),所以所求概率P=.
(3) 点M在⊙O上或⊙O外的点为(0,-2),(1,-2),(2,-1),(2,-2),(2,0),
所以过点M能作⊙O的切线的概率P=.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
