第2章对称图形——圆达标检测卷(含答案) 2025-2026学年数学苏科版九年级上册
文档属性
| 名称 | 第2章对称图形——圆达标检测卷(含答案) 2025-2026学年数学苏科版九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 416.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-19 23:23:03 | ||
图片预览



文档简介
第2章 对称图形——圆 达标检测卷
(时间:120分钟 满分:150分)
一、 选择题(每小题3分,共24分)
1. 若⊙O的半径为3,点P在⊙O外,点P到圆心的距离为d,则d需要满足的条件是( )
A. d>3 B. d=3 C. 0<d<3 D. 无法确定
2. (2024临夏州)如图,AB是⊙O的直径,∠E=35°,则∠BOD等于( )
A. 80° B. 100° C. 120° D. 110°
(第2题) (第3题) (第5题)
3. 如图,⊙O的半径为6,AB,BC是⊙O的弦,若∠ABC=60°,则的长是( )
A. 3π B. 4π C. 10π D. 12π
4. 已知等边三角形ABC的边长为2,则它的内切圆直径为( )
A. 2 B. C. 2 D. 4
5. 如图,⊙O是△ABC的外接圆,半径为4,连接OB,OC,OA,若∠CAO=40°,∠ACB=70°,则阴影部分的面积是( )
A. B. C. D.
6. 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD,BE,CE,若∠CBD=25°,则∠BEC的度数为( )
A. 100° B. 110° C. 115° D. 120°
(第6题) (第7题) (第8题)
7. 如图,在平面直角坐标系xOy中,点P在第一象限,⊙P与x轴,y轴都相切,且经过矩形AOBC的顶点C,与BC相交于点D.若⊙P的半径为5,点A的坐标是(0,8),则点D的坐标是( )
A. (9,2) B. (9,3) C. (10,2) D. (10,3)
8. 如图,四边形ABCD内接于⊙O,AE⊥CB交CB的延长线于点E,若BA平分∠DBE,AD=5,CE=,则AE的长度为( )
A. 3 B. 3 C. 4 D. 2
二、 填空题(每小题3分,共24分)
9. (2024盐城东台期中)已知圆的一条弦把圆周分成1∶3两部分,则这条弦所对的圆周角的度数是________.
10. (2024南京秦淮模拟)已知圆锥的底面半径为3,母线长为6,则此圆锥侧面展开图的圆心角是________.
11. (2024无锡惠山月考)如图,一条公路的转弯处是一段圆弧,点O是这段弧所在圆的圆心.C是上的点,OC⊥AB,垂足为M.若AB=12 m,CM=2 m,则⊙O的半径为________m.
(第11题) (第12题) (第13题) (第14题) (第15题)
12. (2024泰州姜堰期中)如图,AB,CD为⊙O的两条弦,且AB=CD,AB⊥CD,垂足为E,若的长为2π,则AE2+BE2=________.
13. (2024南京秦淮期中)如图,PA,PB分别与⊙O相切,切点分别为A,B,点C在上,过点C的切线分别交PA,PB于点D,E.若PA=10,则△PDE的周长为________.
14. 如图,AB是半圆O的直径,AB=12,AC为弦,OD⊥AC于点D,OE∥AC交半圆O于点E,EF⊥AB于点F,若BF=3,则AC的长为________.
15. 如图,在△ABC 中,AB=AC=6 cm,∠BAC=50°,以AB为直径作半圆,交BC于点D,交AC于点E,则弧DE的长为________cm.
16. 如图,在⊙O中,AB为直径,C为⊙O上的一点,将劣弧沿弦AC翻折交AB于点D,连接CD.若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数为________.
三、 解答题(共102分)
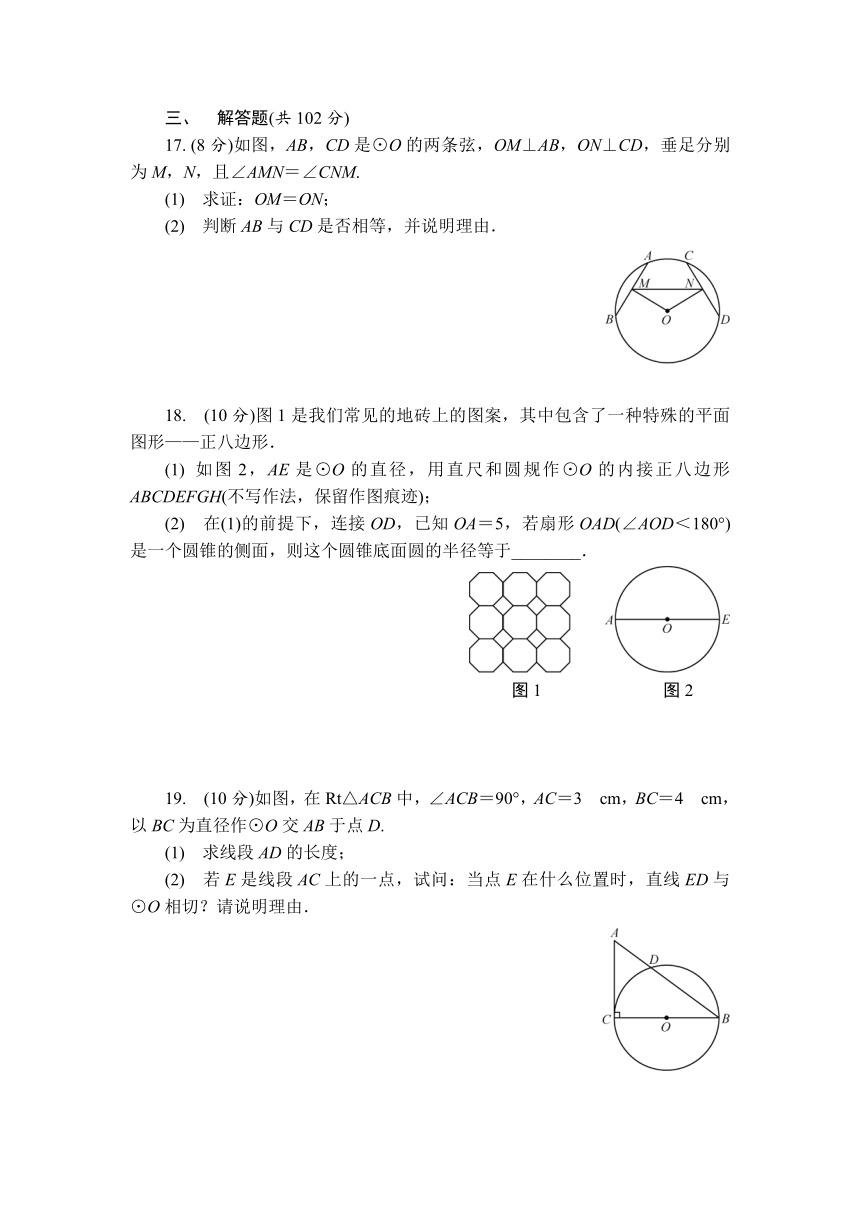
17. (8分)如图,AB,CD是⊙O的两条弦,OM⊥AB,ON⊥CD,垂足分别为M,N,且∠AMN=∠CNM.
(1) 求证:OM=ON;
(2) 判断AB与CD是否相等,并说明理由.
18. (10分)图1是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形.
(1) 如图2,AE是⊙O的直径,用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹);
(2) 在(1)的前提下,连接OD,已知OA=5,若扇形OAD(∠AOD<180°)是一个圆锥的侧面,则这个圆锥底面圆的半径等于________.
图1 图2
19. (10分)如图,在Rt△ACB中,∠ACB=90°,AC=3 cm,BC=4 cm,以BC为直径作⊙O交AB于点D.
(1) 求线段AD的长度;
(2) 若E是线段AC上的一点,试问:当点E在什么位置时,直线ED与⊙O相切?请说明理由.
20. (10分)如图,△ABC内接于⊙O,CO的延长线交AB于点D,交⊙O于点E,交⊙O的切线AF于点F,且AF∥BC.求证:
(1) AO∥BE;
(2) AO平分∠BAC.
21. (10分)如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.
(1) 求证:DE=DB;
(2) 若∠BAC=90°,BD=5,求△ABC外接圆的半径.
22. (10分)如图,OA,OB,OC都是⊙O的半径,∠ACB=2∠BAC.
(1) 求证:∠AOB=2∠BOC;
(2) 若AB=4,BC=,求⊙O的半径.
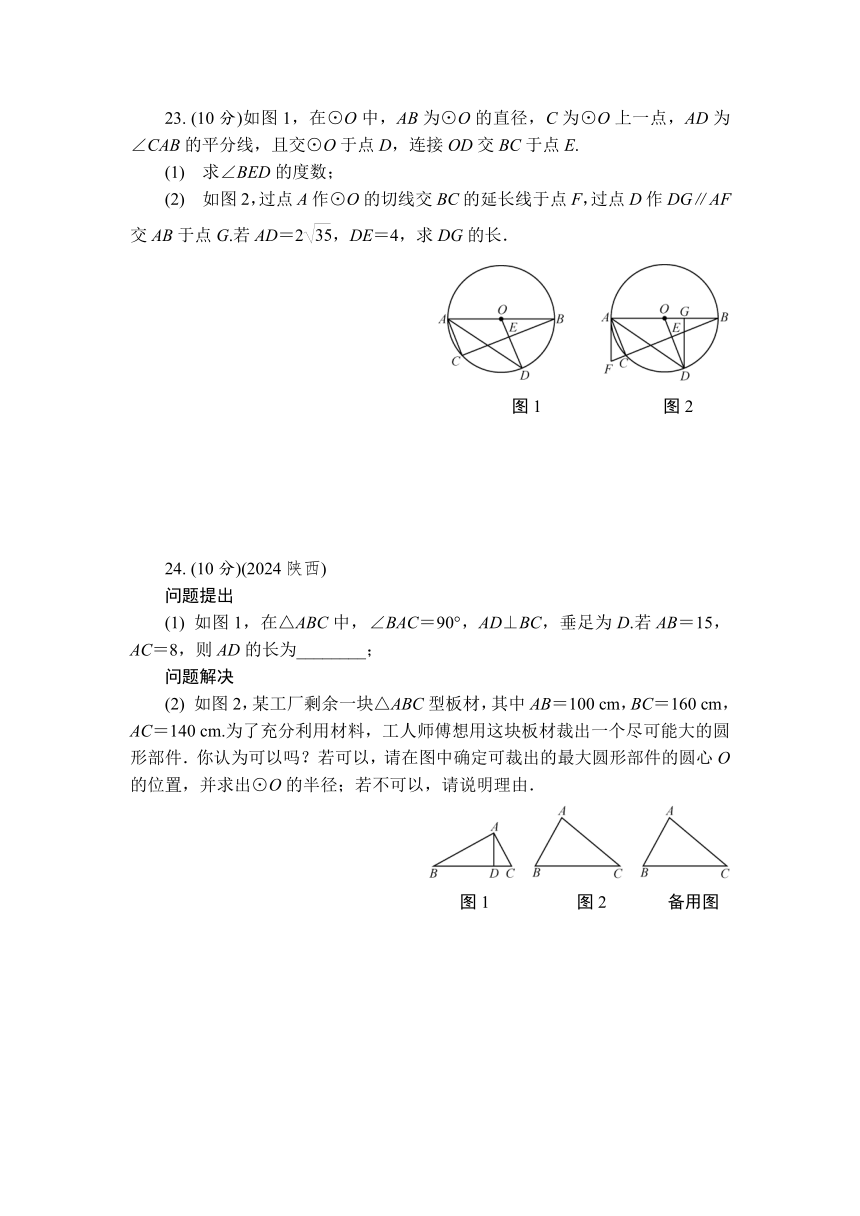
23. (10分)如图1,在⊙O中,AB为⊙O的直径,C为⊙O上一点,AD为∠CAB的平分线,且交⊙O于点D,连接OD交BC于点E.
(1) 求∠BED的度数;
(2) 如图2,过点A作⊙O的切线交BC的延长线于点F,过点D作DG∥AF交AB于点G.若AD=2,DE=4,求DG的长.
图1 图2
24. (10分)(2024陕西)
问题提出
(1) 如图1,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D.若AB=15,AC=8,则AD的长为________;
问题解决
(2) 如图2,某工厂剩余一块△ABC型板材,其中AB=100 cm,BC=160 cm,AC=140 cm.为了充分利用材料,工人师傅想用这块板材裁出一个尽可能大的圆形部件.你认为可以吗?若可以,请在图中确定可裁出的最大圆形部件的圆心O的位置,并求出⊙O的半径;若不可以,请说明理由.
图1 图2 备用图
25. (12分)(2024德州)如图,⊙O1与⊙O2都经过A,B两点,点O2在⊙O1上,C是上的一点,连接AC并延长交⊙O2于点P,连接AB,BC,BP.
(1) 求证:∠ACB=2∠P;
(2) 若∠P=30°,AB=2.
①求⊙O1的半径;
②求图中阴影部分的面积.
26. (12分)如图1,OA是⊙O的半径,D为OA上的动点,过点D作线段CD⊥OA交⊙O于点F,过点C作⊙O的切线BC,B为切点,连接AB,交CD于点E.
(1) 求证:CB=CE;
(2) 如图2,当D运动到OA的中点时,CD刚好平分,求证:△BCE是等边三角形;
(3) 如图3,当D运动到点O时,若⊙O的半径为2,且∠DCB=45°,求线段EF的长.
图1 图2 图3
第2章对称图形——圆达标检测卷
1. A 2. D 3. B 4. C 5. C 6. C 7. A 8. D
9. 45°或135° 10. 180° 11. 10 12. 32 13. 20
14. 6 15. 16. 40°
17. (1) 证明:因为OM⊥AB,ON⊥CD,
所以∠AMO=∠CNO=90°.
因为∠AMN=∠CNM,
所以∠OMN=∠ONM,所以MO=NO.
(2) 解:AB=CD.理由如下:
如图,连接OA,OC.
因为OM⊥AB,ON⊥CD,
所以AM=AB,CN=CD,∠AMO=∠CNO=90°.
在Rt△AOM与Rt△CON中,
所以Rt△AOM≌Rt△CON(HL),
所以AM=CN,所以AB=CD.
18. 解:(1) 如图,八边形ABCDEFGH即为所求.
(2)
19. 解:(1) 如图,连接CD.
因为BC为⊙O的直径,
所以∠BDC=∠ADC=90°,即CD⊥AB.
因为∠ACB=90°,AC=3 cm,BC=4 cm,
所以AB==5(cm).
因为S△ABC=AB·CD=AC·BC,
所以CD==(cm),
所以在Rt△ADC中,AD===(cm).
(2) 当E是AC的中点时,直线ED与⊙O相切.理由如下:
如图,连接OD,取AC的中点E,连接DE.
因为在Rt△ADC中,∠ADC=90°,E是AC的中点,
所以ED=EC,所以∠EDC=∠ECD.
因为OC=OD,所以∠ODC=∠OCD,
所以∠EDO=∠EDC+∠ODC=∠ECD+∠OCD=∠ACB=90°,
所以ED⊥OD.
又因为OD是⊙O的半径,
所以直线ED与⊙O相切.
20. 证明:(1) 因为AF是⊙O的切线,所以AF⊥OA,
即∠OAF=90°.
因为CE是⊙O的直径,
所以∠CBE=90°,所以∠OAF=∠CBE=90°.
因为AF∥BC,所以∠BAF=∠ABC,
所以∠OAF-∠BAF=∠CBE-∠ABC,
即∠OAB=∠ABE,所以AO∥BE.
(2) 因为∠ABE 与∠ACE 都是所对的圆周角,
所以∠ABE=∠ACE.
因为OA=OC,所以∠ACE=∠OAC,
所以∠ABE=∠OAC.
由(1)知,∠OAB=∠ABE,
所以∠OAB=∠OAC,所以AO平分∠BAC.
21. (1) 证明:因为AD平分∠BAC,BE平分∠ABC,
所以∠BAE=∠CAD,∠ABE=∠CBE,
所以=.
因为∠DBC=∠CAD,所以∠DBC=∠BAE.
因为∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,
所以∠DBE=∠DEB,所以DE=DB.
(2) 解:连接CD.
由(1),得=,所以CD=BD=5.
因为∠BAC=90°,所以BC为外接圆的直径,
所以∠BDC=90°,
所以BC==5,
所以△ABC外接圆的半径r=×5=.
22. (1) 证明:因为∠ACB=∠AOB,∠BAC=∠BOC,∠ACB=2∠BAC,
所以∠AOB=2∠BOC.
(2) 解:过点O作半径OD⊥AB于点E,连接BD,则AE=BE.
因为∠AOB=2∠BOC,∠DOB=∠AOB,
所以∠DOB=∠BOC,所以BD=BC.
因为AB=4,BC=,所以BE=2,DB=.
在Rt△BDE 中,∠DEB=90°,
所以DE==1,
在Rt△BOE中,∠OEB=90°,
所以OB2=OE2+BE2,即OB2=(OB-1)2+22,
解得OB=,
所以⊙O的半径是 .
23. 解:(1) 因为AB为⊙O的直径,所以∠ACB=90°.
因为AD为∠CAB的平分线,所以∠BAC=2∠BAD.
因为OA=OD,所以∠BAD=∠ODA,
所以∠BOD=∠BAD+∠ODA=2∠BAD,
所以∠BOD=∠BAC,所以OD∥AC,
所以∠OEB=∠ACB=90°,所以∠BED=90°.
(2) 连接BD,设OA=OB=OD=r,
则OE=r-4,AC=2OE=2r-8,AB=2r.
因为AB为⊙O的直径,所以∠ADB=90°.
在Rt△ADB中,BD2=AB2-AD2,
由(1),得∠BED=90°,所以∠BED=∠BEO=90°,
所以BE2=OB2-OE2,BE2=BD2-DE2,
所以BD2=AB2-AD2=BE2+DE2=OB2-OE2+DE2,
所以(2r)2-(2)2=r2-(r-4)2+42,
解得r1=7,r2=-5(不符合题意,舍去),
所以AB=2r=14,
所以BD===2.
因为AF是⊙O的切线,所以AF⊥AB.
因为DG∥AF,所以DG⊥AB,
所以S△ABD=AD·BD=AB·DG,
所以DG===2.
24. 解:(1)
(2) 可以.理由如下:
因为三角形内最大的圆是三角形的内切圆,
所以所求圆的圆心是△ABC的内心,
作∠ABC和∠ACB的平分线BE,CF交于点O,
则点O就是裁出的最大圆形部件的圆心O的位置,
过点O作OH⊥BC于点H,OP⊥AC于点P,OQ⊥AB于点Q,连接OA,OB,OC,过点A作AM⊥BC于点M,如图所示.
设BM=x cm,⊙O的半径为R cm,
因为AB=100 cm,BC=160 cm,AC=140 cm,
所以CM=(160-x) cm,
在Rt△ABM中,由勾股定理,得AM2=AB2-BM2=1002-x2,
在Rt△ACM中,由勾股定理,得AM2=AC2-CM2=1402-(160-x)2,
所以1002-x2=1402-(160-x)2,
解得x=50,
所以AM==50(cm),
所以S△ABC=BC·AM=×160×50=4 000(cm2).
因为点O为△ABC的内心,
所以OH=OP=OQ=R cm.
因为S△OBC+S△OCA+S△OAB=S△ABC,
所以BC·OH+AC·OP+AB·OQ=4 000,
即(100+160+140)R=8 000,
解得R=20 cm,
所以⊙O的半径为20 cm.
25. (1) 证明:连接AO2,BO2.
因为=,
所以∠ACB=∠AO2B=2∠P.
(2) 解:①连接AO1并延长交⊙O1于点D,连接BD,
则∠ABD=90°.
因为∠P=30°,
所以∠AO2B=2∠P=60°,
所以∠D=∠AO2B=60°.
因为AB=2,
所以AD=4,
所以⊙O1的半径为2.
②连接O2O1并延长交AB于点H,
则AH=AB=,O2H⊥AB,
所以HO1=AH=1,AO1=2,
所以O2H=3.
在⊙O2中,弓形AB的面积=扇形AO2B的面积-△AO2B的面积=-×2×3=2π-3;
在⊙O1中,弓形AB的面积=扇形AO1B的面积-△AO1B的面积=-×2×1=-,
故图中阴影部分的面积为(-)-2π+3=2-
26. (1) 证明:连接OB.
因为CB为⊙O的切线,切点为B,
所以OB⊥BC,所以∠OBC=90°.
因为OA=OB,所以∠DAE=∠OBA.
因为∠DAE+∠DEA=90°,∠OBA+∠CBE=90°,
所以∠DEA=∠CBE.
因为∠CEB=∠DEA,
所以∠CEB=∠CBE,所以CB=CE.
(2) 证明:连接OF,OB.
在Rt△ODF中,OF=OA=2OD,
所以∠OFD=30°,所以∠DOF=60°.
因为CD刚好平分,
所以∠AOB=2∠AOF=120°,
所以∠C=360°-∠ODC-∠OBC-∠AOB=60°.
因为CB=CE,所以△BCE是等边三角形.
(3) 解:连接OB.
因为∠OBC=90°,∠DCB=45°,
所以△OBC为等腰直角三角形,
所以BC=OB=2,OC=2 .
又因为CB=CE,
所以OE=OC-CE=OC-BC=2 -2,
所以EF=OF-OE=2-(2 -2)=4-2 .
(时间:120分钟 满分:150分)
一、 选择题(每小题3分,共24分)
1. 若⊙O的半径为3,点P在⊙O外,点P到圆心的距离为d,则d需要满足的条件是( )
A. d>3 B. d=3 C. 0<d<3 D. 无法确定
2. (2024临夏州)如图,AB是⊙O的直径,∠E=35°,则∠BOD等于( )
A. 80° B. 100° C. 120° D. 110°
(第2题) (第3题) (第5题)
3. 如图,⊙O的半径为6,AB,BC是⊙O的弦,若∠ABC=60°,则的长是( )
A. 3π B. 4π C. 10π D. 12π
4. 已知等边三角形ABC的边长为2,则它的内切圆直径为( )
A. 2 B. C. 2 D. 4
5. 如图,⊙O是△ABC的外接圆,半径为4,连接OB,OC,OA,若∠CAO=40°,∠ACB=70°,则阴影部分的面积是( )
A. B. C. D.
6. 如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD,BE,CE,若∠CBD=25°,则∠BEC的度数为( )
A. 100° B. 110° C. 115° D. 120°
(第6题) (第7题) (第8题)
7. 如图,在平面直角坐标系xOy中,点P在第一象限,⊙P与x轴,y轴都相切,且经过矩形AOBC的顶点C,与BC相交于点D.若⊙P的半径为5,点A的坐标是(0,8),则点D的坐标是( )
A. (9,2) B. (9,3) C. (10,2) D. (10,3)
8. 如图,四边形ABCD内接于⊙O,AE⊥CB交CB的延长线于点E,若BA平分∠DBE,AD=5,CE=,则AE的长度为( )
A. 3 B. 3 C. 4 D. 2
二、 填空题(每小题3分,共24分)
9. (2024盐城东台期中)已知圆的一条弦把圆周分成1∶3两部分,则这条弦所对的圆周角的度数是________.
10. (2024南京秦淮模拟)已知圆锥的底面半径为3,母线长为6,则此圆锥侧面展开图的圆心角是________.
11. (2024无锡惠山月考)如图,一条公路的转弯处是一段圆弧,点O是这段弧所在圆的圆心.C是上的点,OC⊥AB,垂足为M.若AB=12 m,CM=2 m,则⊙O的半径为________m.
(第11题) (第12题) (第13题) (第14题) (第15题)
12. (2024泰州姜堰期中)如图,AB,CD为⊙O的两条弦,且AB=CD,AB⊥CD,垂足为E,若的长为2π,则AE2+BE2=________.
13. (2024南京秦淮期中)如图,PA,PB分别与⊙O相切,切点分别为A,B,点C在上,过点C的切线分别交PA,PB于点D,E.若PA=10,则△PDE的周长为________.
14. 如图,AB是半圆O的直径,AB=12,AC为弦,OD⊥AC于点D,OE∥AC交半圆O于点E,EF⊥AB于点F,若BF=3,则AC的长为________.
15. 如图,在△ABC 中,AB=AC=6 cm,∠BAC=50°,以AB为直径作半圆,交BC于点D,交AC于点E,则弧DE的长为________cm.
16. 如图,在⊙O中,AB为直径,C为⊙O上的一点,将劣弧沿弦AC翻折交AB于点D,连接CD.若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数为________.
三、 解答题(共102分)
17. (8分)如图,AB,CD是⊙O的两条弦,OM⊥AB,ON⊥CD,垂足分别为M,N,且∠AMN=∠CNM.
(1) 求证:OM=ON;
(2) 判断AB与CD是否相等,并说明理由.
18. (10分)图1是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形.
(1) 如图2,AE是⊙O的直径,用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹);
(2) 在(1)的前提下,连接OD,已知OA=5,若扇形OAD(∠AOD<180°)是一个圆锥的侧面,则这个圆锥底面圆的半径等于________.
图1 图2
19. (10分)如图,在Rt△ACB中,∠ACB=90°,AC=3 cm,BC=4 cm,以BC为直径作⊙O交AB于点D.
(1) 求线段AD的长度;
(2) 若E是线段AC上的一点,试问:当点E在什么位置时,直线ED与⊙O相切?请说明理由.
20. (10分)如图,△ABC内接于⊙O,CO的延长线交AB于点D,交⊙O于点E,交⊙O的切线AF于点F,且AF∥BC.求证:
(1) AO∥BE;
(2) AO平分∠BAC.
21. (10分)如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.
(1) 求证:DE=DB;
(2) 若∠BAC=90°,BD=5,求△ABC外接圆的半径.
22. (10分)如图,OA,OB,OC都是⊙O的半径,∠ACB=2∠BAC.
(1) 求证:∠AOB=2∠BOC;
(2) 若AB=4,BC=,求⊙O的半径.
23. (10分)如图1,在⊙O中,AB为⊙O的直径,C为⊙O上一点,AD为∠CAB的平分线,且交⊙O于点D,连接OD交BC于点E.
(1) 求∠BED的度数;
(2) 如图2,过点A作⊙O的切线交BC的延长线于点F,过点D作DG∥AF交AB于点G.若AD=2,DE=4,求DG的长.
图1 图2
24. (10分)(2024陕西)
问题提出
(1) 如图1,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D.若AB=15,AC=8,则AD的长为________;
问题解决
(2) 如图2,某工厂剩余一块△ABC型板材,其中AB=100 cm,BC=160 cm,AC=140 cm.为了充分利用材料,工人师傅想用这块板材裁出一个尽可能大的圆形部件.你认为可以吗?若可以,请在图中确定可裁出的最大圆形部件的圆心O的位置,并求出⊙O的半径;若不可以,请说明理由.
图1 图2 备用图
25. (12分)(2024德州)如图,⊙O1与⊙O2都经过A,B两点,点O2在⊙O1上,C是上的一点,连接AC并延长交⊙O2于点P,连接AB,BC,BP.
(1) 求证:∠ACB=2∠P;
(2) 若∠P=30°,AB=2.
①求⊙O1的半径;
②求图中阴影部分的面积.
26. (12分)如图1,OA是⊙O的半径,D为OA上的动点,过点D作线段CD⊥OA交⊙O于点F,过点C作⊙O的切线BC,B为切点,连接AB,交CD于点E.
(1) 求证:CB=CE;
(2) 如图2,当D运动到OA的中点时,CD刚好平分,求证:△BCE是等边三角形;
(3) 如图3,当D运动到点O时,若⊙O的半径为2,且∠DCB=45°,求线段EF的长.
图1 图2 图3
第2章对称图形——圆达标检测卷
1. A 2. D 3. B 4. C 5. C 6. C 7. A 8. D
9. 45°或135° 10. 180° 11. 10 12. 32 13. 20
14. 6 15. 16. 40°
17. (1) 证明:因为OM⊥AB,ON⊥CD,
所以∠AMO=∠CNO=90°.
因为∠AMN=∠CNM,
所以∠OMN=∠ONM,所以MO=NO.
(2) 解:AB=CD.理由如下:
如图,连接OA,OC.
因为OM⊥AB,ON⊥CD,
所以AM=AB,CN=CD,∠AMO=∠CNO=90°.
在Rt△AOM与Rt△CON中,
所以Rt△AOM≌Rt△CON(HL),
所以AM=CN,所以AB=CD.
18. 解:(1) 如图,八边形ABCDEFGH即为所求.
(2)
19. 解:(1) 如图,连接CD.
因为BC为⊙O的直径,
所以∠BDC=∠ADC=90°,即CD⊥AB.
因为∠ACB=90°,AC=3 cm,BC=4 cm,
所以AB==5(cm).
因为S△ABC=AB·CD=AC·BC,
所以CD==(cm),
所以在Rt△ADC中,AD===(cm).
(2) 当E是AC的中点时,直线ED与⊙O相切.理由如下:
如图,连接OD,取AC的中点E,连接DE.
因为在Rt△ADC中,∠ADC=90°,E是AC的中点,
所以ED=EC,所以∠EDC=∠ECD.
因为OC=OD,所以∠ODC=∠OCD,
所以∠EDO=∠EDC+∠ODC=∠ECD+∠OCD=∠ACB=90°,
所以ED⊥OD.
又因为OD是⊙O的半径,
所以直线ED与⊙O相切.
20. 证明:(1) 因为AF是⊙O的切线,所以AF⊥OA,
即∠OAF=90°.
因为CE是⊙O的直径,
所以∠CBE=90°,所以∠OAF=∠CBE=90°.
因为AF∥BC,所以∠BAF=∠ABC,
所以∠OAF-∠BAF=∠CBE-∠ABC,
即∠OAB=∠ABE,所以AO∥BE.
(2) 因为∠ABE 与∠ACE 都是所对的圆周角,
所以∠ABE=∠ACE.
因为OA=OC,所以∠ACE=∠OAC,
所以∠ABE=∠OAC.
由(1)知,∠OAB=∠ABE,
所以∠OAB=∠OAC,所以AO平分∠BAC.
21. (1) 证明:因为AD平分∠BAC,BE平分∠ABC,
所以∠BAE=∠CAD,∠ABE=∠CBE,
所以=.
因为∠DBC=∠CAD,所以∠DBC=∠BAE.
因为∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAE,
所以∠DBE=∠DEB,所以DE=DB.
(2) 解:连接CD.
由(1),得=,所以CD=BD=5.
因为∠BAC=90°,所以BC为外接圆的直径,
所以∠BDC=90°,
所以BC==5,
所以△ABC外接圆的半径r=×5=.
22. (1) 证明:因为∠ACB=∠AOB,∠BAC=∠BOC,∠ACB=2∠BAC,
所以∠AOB=2∠BOC.
(2) 解:过点O作半径OD⊥AB于点E,连接BD,则AE=BE.
因为∠AOB=2∠BOC,∠DOB=∠AOB,
所以∠DOB=∠BOC,所以BD=BC.
因为AB=4,BC=,所以BE=2,DB=.
在Rt△BDE 中,∠DEB=90°,
所以DE==1,
在Rt△BOE中,∠OEB=90°,
所以OB2=OE2+BE2,即OB2=(OB-1)2+22,
解得OB=,
所以⊙O的半径是 .
23. 解:(1) 因为AB为⊙O的直径,所以∠ACB=90°.
因为AD为∠CAB的平分线,所以∠BAC=2∠BAD.
因为OA=OD,所以∠BAD=∠ODA,
所以∠BOD=∠BAD+∠ODA=2∠BAD,
所以∠BOD=∠BAC,所以OD∥AC,
所以∠OEB=∠ACB=90°,所以∠BED=90°.
(2) 连接BD,设OA=OB=OD=r,
则OE=r-4,AC=2OE=2r-8,AB=2r.
因为AB为⊙O的直径,所以∠ADB=90°.
在Rt△ADB中,BD2=AB2-AD2,
由(1),得∠BED=90°,所以∠BED=∠BEO=90°,
所以BE2=OB2-OE2,BE2=BD2-DE2,
所以BD2=AB2-AD2=BE2+DE2=OB2-OE2+DE2,
所以(2r)2-(2)2=r2-(r-4)2+42,
解得r1=7,r2=-5(不符合题意,舍去),
所以AB=2r=14,
所以BD===2.
因为AF是⊙O的切线,所以AF⊥AB.
因为DG∥AF,所以DG⊥AB,
所以S△ABD=AD·BD=AB·DG,
所以DG===2.
24. 解:(1)
(2) 可以.理由如下:
因为三角形内最大的圆是三角形的内切圆,
所以所求圆的圆心是△ABC的内心,
作∠ABC和∠ACB的平分线BE,CF交于点O,
则点O就是裁出的最大圆形部件的圆心O的位置,
过点O作OH⊥BC于点H,OP⊥AC于点P,OQ⊥AB于点Q,连接OA,OB,OC,过点A作AM⊥BC于点M,如图所示.
设BM=x cm,⊙O的半径为R cm,
因为AB=100 cm,BC=160 cm,AC=140 cm,
所以CM=(160-x) cm,
在Rt△ABM中,由勾股定理,得AM2=AB2-BM2=1002-x2,
在Rt△ACM中,由勾股定理,得AM2=AC2-CM2=1402-(160-x)2,
所以1002-x2=1402-(160-x)2,
解得x=50,
所以AM==50(cm),
所以S△ABC=BC·AM=×160×50=4 000(cm2).
因为点O为△ABC的内心,
所以OH=OP=OQ=R cm.
因为S△OBC+S△OCA+S△OAB=S△ABC,
所以BC·OH+AC·OP+AB·OQ=4 000,
即(100+160+140)R=8 000,
解得R=20 cm,
所以⊙O的半径为20 cm.
25. (1) 证明:连接AO2,BO2.
因为=,
所以∠ACB=∠AO2B=2∠P.
(2) 解:①连接AO1并延长交⊙O1于点D,连接BD,
则∠ABD=90°.
因为∠P=30°,
所以∠AO2B=2∠P=60°,
所以∠D=∠AO2B=60°.
因为AB=2,
所以AD=4,
所以⊙O1的半径为2.
②连接O2O1并延长交AB于点H,
则AH=AB=,O2H⊥AB,
所以HO1=AH=1,AO1=2,
所以O2H=3.
在⊙O2中,弓形AB的面积=扇形AO2B的面积-△AO2B的面积=-×2×3=2π-3;
在⊙O1中,弓形AB的面积=扇形AO1B的面积-△AO1B的面积=-×2×1=-,
故图中阴影部分的面积为(-)-2π+3=2-
26. (1) 证明:连接OB.
因为CB为⊙O的切线,切点为B,
所以OB⊥BC,所以∠OBC=90°.
因为OA=OB,所以∠DAE=∠OBA.
因为∠DAE+∠DEA=90°,∠OBA+∠CBE=90°,
所以∠DEA=∠CBE.
因为∠CEB=∠DEA,
所以∠CEB=∠CBE,所以CB=CE.
(2) 证明:连接OF,OB.
在Rt△ODF中,OF=OA=2OD,
所以∠OFD=30°,所以∠DOF=60°.
因为CD刚好平分,
所以∠AOB=2∠AOF=120°,
所以∠C=360°-∠ODC-∠OBC-∠AOB=60°.
因为CB=CE,所以△BCE是等边三角形.
(3) 解:连接OB.
因为∠OBC=90°,∠DCB=45°,
所以△OBC为等腰直角三角形,
所以BC=OB=2,OC=2 .
又因为CB=CE,
所以OE=OC-CE=OC-BC=2 -2,
所以EF=OF-OE=2-(2 -2)=4-2 .
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
