2024-2025学年重庆市万州第三中学等多校联考高一下学期5月月考数学试题(含解析)
文档属性
| 名称 | 2024-2025学年重庆市万州第三中学等多校联考高一下学期5月月考数学试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 583.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 00:00:00 | ||
图片预览




文档简介
2024-2025学年重庆市万州第三中学等多校联考高一下学期5月月考数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若复数的实部与虚部之和为0,则b的值为
A. 2 B. C. D.
2.在四棱锥中,已知平面ABCD,底面ABCD是菱形,,则异面直线PB与CD所成的角为
A. B. C. D.
3.在中,点D在BC边上,且,则
A. B.
C. D.
4.下列说法正确的是( )
A. 数据1,8,3,5,6的第60百分位数是5
B. 若一组样本数据4,6,7,8,9,a的平均数为7,则
C. 用分层随机抽样时,个体数最多的层里的个体被抽到的概率最大
D. 若的标准差为4,则的标准差是8
5.已知向量,满足,且,则向量在向量上的投影向量为
A. B. C. D.
6.我国在2024年的全国发电装机容量为亿千瓦,包括水电、火电、核电、风电、太阳能发电,其占比如图所示,根据此扇形图,下面说法正确的是( )
A. 2024年我国太阳能发电装机容量部分的扇形圆心角小于
B. 2024年我国火电发电装机容量超过15亿千瓦
C. 2024年我国火电发电装机容量超过新能源太阳能、风电、核电的发电装机容量
D. 若2025年核电规模要达到2024年全国发电装机容量规模的,则还要再建设的核电的发电装机容量为亿千瓦
7.如图,三棱锥的底面的斜二测直观图为,已知底面ABC,,,,则三棱锥外接球的表面积S为
A. B. C. D.
8.在锐角中,内角A,B,C的对边分别为a,b,c,已知,,则AB边上的高的取值范围为
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得2分,有选错的得0分。
9.已知m,n为两条不同的直线,,为两个不同的平面,下列命题正确的是
A. 若,,则
B. 若,,,,则
C. 若,,,则
D. 若,,,则
10.已知的内角A,B,C的对边分别为a,b,c,下列说法正确的是
A. 若,则
B. 若,,,则三角形有两解
C. 若的面积,则
D. 若,则为等腰三角形或直角三角形
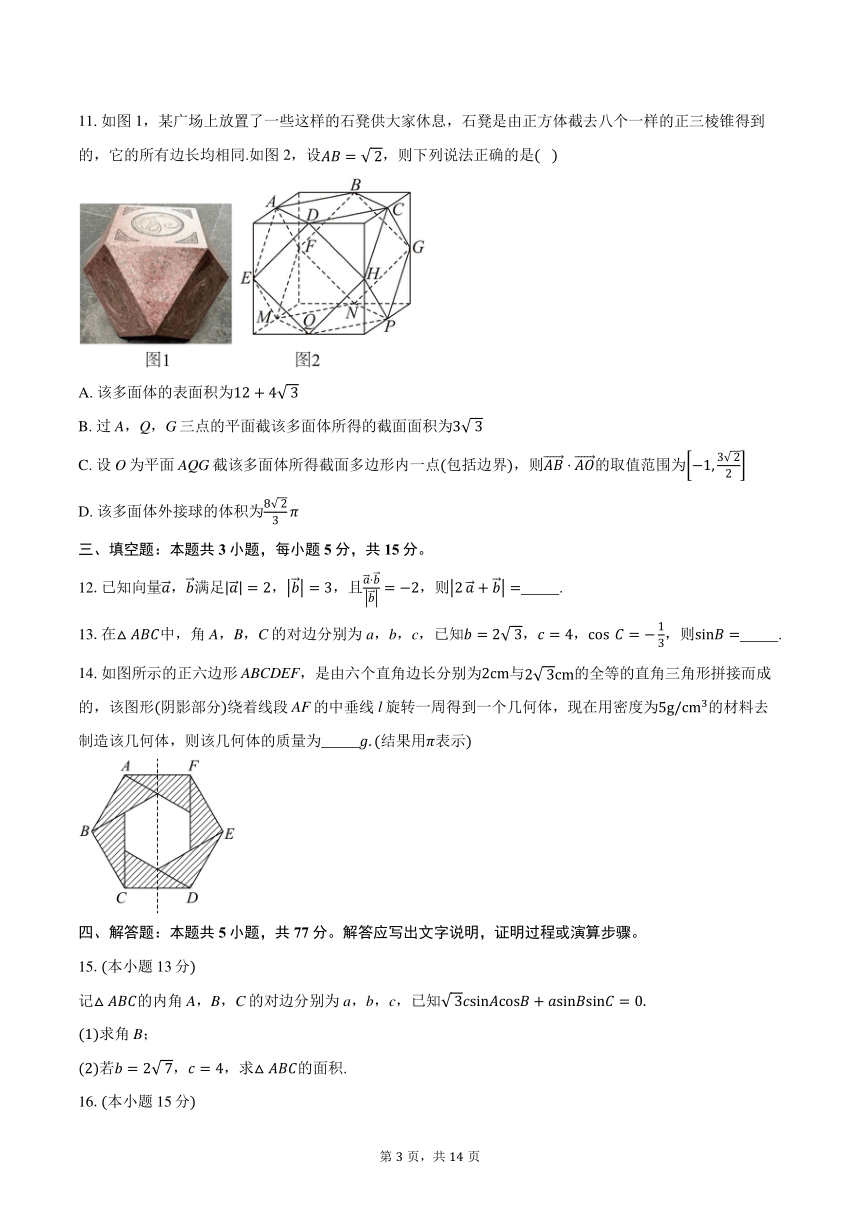
11.如图1,某广场上放置了一些这样的石凳供大家休息,石凳是由正方体截去八个一样的正三棱锥得到的,它的所有边长均相同.如图2,设,则下列说法正确的是
A. 该多面体的表面积为
B. 过A,Q,G三点的平面截该多面体所得的截面面积为
C. 设O为平面AQG截该多面体所得截面多边形内一点包括边界,则的取值范围为
D. 该多面体外接球的体积为
三、填空题:本题共3小题,每小题5分,共15分。
12.已知向量,满足,,且,则 .
13.在中,角A,B,C的对边分别为a,b,c,已知,,,则 .
14.如图所示的正六边形ABCDEF,是由六个直角边长分别为与的全等的直角三角形拼接而成的,该图形阴影部分绕着线段AF的中垂线l旋转一周得到一个几何体,现在用密度为的材料去制造该几何体,则该几何体的质量为 结果用表示
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题13分
记的内角A,B,C的对边分别为a,b,c,已知
求角B;
若,,求的面积.
16.本小题15分
如图,在直四棱柱中,底面ABCD是矩形,,E,F分别是棱AD,BC的中点.
证明:平面
证明:平面平面
17.本小题15分
已知平面向量,将的起点放在坐标原点O处,然后将按逆时针方向旋转得到的向量为,设向量,
若,求实数t的值;
将向量与的起点放在O处,,,若与的夹角为,求的面积.
18.本小题17分
2025年4月19日,全球首个“人形机器人”半程马拉松在北京举行,某机构调查了1000名观众,将这1000名观众对“人形机器人”的评分数据分成,六组,得到如图所示的频率分布直方图.
求频率分布直方图中评分的中位数;
已知评分在这两区间内数据的方差分别为,,且每组以该组的中间值作为该组的平均值,现将评分在这两区间内的数据合在一起得到一组新的数据,求这组新数据的方差结果用分数表示
19.本小题17分
如图,在三棱锥中,由AB,AC,AD三条射线所构成的图形被称为“三面角”,设,,,设二面角的平面角为,则有
已知三棱锥的所有棱长均为1,求二面角的余弦值.
设直线AD与平面ABC所成的角为,证明
若,,,,,求点A到平面BCD的距离.
答案和解析
1.【答案】A
【解析】解:由复数的实部与虚部之和为0,
得,即
故选:
2.【答案】C
【解析】解:因为,所以为异面直线PB与CD所成的角.
因为平面ABCD,平面ABCD,所以
又,所以
故选:
3.【答案】B
【解析】解:如图,
故选:
4.【答案】D
【解析】解:对于A,因为5个数据从小到大排列为1,3,5,6,8,且,所以第60百分位数是,则A错误.
对于B,一组样本数据4,6,7,8,9,a的平均数为7,可知,解得,B错误.
对于C,因为在分层抽样中,每一层的抽样比是相同的,都等于总的抽样比,所以C错误.
对于D,因为的标准差为4,所以它的方差为16,
而的方差为,所以它的标准差是8,故D正确.
故选:
5.【答案】B
【解析】解:向量在向量上的投影向量为
故选:
6.【答案】D
【解析】解:对于A:太阳能发电装机容量占,超过,则扇形圆心角大于,所以A错误;
对于B:2024年我国火电发电装机容量占,因为,所以B错误;
对于C:2024年我国火电发电装机容量占,新能源太阳能、风电、核电的发电装机容量占比和为,所以C错误;
对于D:还要再建设的核电的发电装机容量为亿千瓦,所以D正确.
故选:
7.【答案】B
【解析】解:由题意可知在斜二测直观图中,,,
则,,,
由斜二测画法可得,在中,,,,
在三棱锥中,因为底面ABC,且,
所以可将三棱锥补成相邻的三条侧棱分别为6,4,8的长方体,
则三棱锥的外接球即为该长方体的外接球,
因为长方体的体对角线即为外接球的直径,
则外接球的半径,
故三棱锥外接球的表面积
故选:
8.【答案】C
【解析】解:因为是锐角三角形,所以,解得
由正弦定理可得,则,
设AB边上的高为h,由,
得,
所以
由,得,可得
所以
即AB边上的高的取值范围为
故选:
9.【答案】CD
【解析】解:对于A,若,,则或n与m异面,所以A错误.
对于B,若,,,,没有m,n是相交直线这个条件,不能得到,所以B错误.
对于C,由,得存在过直线m的平面与平面相交,令交线为c,则,而,,则,,因此,C正确.
对于D,若,,则,又,所以,D正确.
故选:
10.【答案】ACD
【解析】解:对于A,由可得,从而,A正确;
对于B,由正弦定理,得,
又因为,所以,所以B只有唯一解,B错误;
对于C,因为,
所以,又,解得,C正确;
对于D,因为,
由正弦定理得,即,
所以或,即或,
则为等腰三角形或直角三角形,D正确.
故选:
11.【答案】ABD
【解析】解:对于A,由,得正方体的棱长,
所以该多面体的表面积,A正确;
对于B,由平面的性质可知过A,Q,G三点的平面截该多面体所得的截面是边长为的正六边形ABGPQE,其面积为,B正确;
对于C,以A为坐标原点,建立如图所示的平面直角坐标系,
则,,设点,且,,
则,,
所以,即,C错误;
对于D,由多面体性质可知其外接球球心为该多面体的体心,
即正方体体心,设为为,
外接球的半径为,
所以该多面体外接球的体积为,D正确.
故选:
12.【答案】1
【解析】解:因为,所以,则,从而
故答案为:
13.【答案】
【解析】解:在中,由,可得
由正弦定理得即,可得
故答案为:
14.【答案】
【解析】解:外部正六边形的边长为,
旋转得到的几何体是两个全等的圆台,
上底面半径为,下底面半径为,高为,
体积为,
内部的六边形边长为2cm,旋转得到的几何体是一个圆柱和两个与圆柱同底的圆锥,
圆锥的底面半径为,高为1cm,圆柱的底面半径为,高为,
内部的六边形旋转得到的几何体的体积为,
所以该几何体的体积为,
用密度为的材料去制造该几何体,
则该几何体的质量为
故答案为:
15.【答案】解:因为,
所以,
因为,所以
又,所以
由,得,
解得负解舍
所以的面积为
【解析】详细解答和解析过程见【答案】
16.【答案】证明:因为E,F分别是矩形ABCD的棱AD,BC的中点,
所以,,
则四边形BEDF是平行四边形,从而,
又平面,平面,
所以平面;
证明:在矩形ABCD中,因为,E,F分别是棱AD,BC的中点,
所以,,,
所以,
从而,即,
因为四棱柱是直四棱柱,
所以平面ABCD,
又平面ABCD,所以,
因为,且平面,
所以平面
又平面,
所以平面平面
【解析】详细解答和解析过程见【答案】
17.【答案】解:根据三角函数的定义知,,
所以,则,
所以,
,
所以,解得
由知,,
由,得,
整理得,解得或
当时,,,
;
当时,,,
综上所述,的面积为或
【解析】详细解答和解析过程见【答案】
18.【答案】解:由图可知,前3个小矩形对应的频率之和为,所以中位数为70分.
对应的平均数为65分,对应的平均数为85分,
因为评分在这两组数据对应的频率为,
所以可以求出整体的平均数为分,
故所求评分的方差
【解析】详细解答和解析过程见【答案】
19.【答案】解:三棱锥的所有棱长均为1,
故,
由已知得;
证明:过点D作平面ABC的垂线,垂足为H,连接AH,则,
设,
在面ABC中,过点 H做于点T,连接DT,
因为平面ABC,平面ABC,所以,
又,平面DHT,
所以平面DHT,
因为平面DHT,所以,
故,又,,
即,
所以①,
在三面角中,同理可得②,
由①得,从而,
由②得,
所以
,
所以,
所以
;
在中,由,得,
故,
在中,由,得,
故,
在中,由,得,
所以,从而
设直线DA与平面BCD所成的角为,
由知,
所以,
则点A到平面BCD的距离为
【解析】详细解答和解析过程见【答案】
第2页,共2页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若复数的实部与虚部之和为0,则b的值为
A. 2 B. C. D.
2.在四棱锥中,已知平面ABCD,底面ABCD是菱形,,则异面直线PB与CD所成的角为
A. B. C. D.
3.在中,点D在BC边上,且,则
A. B.
C. D.
4.下列说法正确的是( )
A. 数据1,8,3,5,6的第60百分位数是5
B. 若一组样本数据4,6,7,8,9,a的平均数为7,则
C. 用分层随机抽样时,个体数最多的层里的个体被抽到的概率最大
D. 若的标准差为4,则的标准差是8
5.已知向量,满足,且,则向量在向量上的投影向量为
A. B. C. D.
6.我国在2024年的全国发电装机容量为亿千瓦,包括水电、火电、核电、风电、太阳能发电,其占比如图所示,根据此扇形图,下面说法正确的是( )
A. 2024年我国太阳能发电装机容量部分的扇形圆心角小于
B. 2024年我国火电发电装机容量超过15亿千瓦
C. 2024年我国火电发电装机容量超过新能源太阳能、风电、核电的发电装机容量
D. 若2025年核电规模要达到2024年全国发电装机容量规模的,则还要再建设的核电的发电装机容量为亿千瓦
7.如图,三棱锥的底面的斜二测直观图为,已知底面ABC,,,,则三棱锥外接球的表面积S为
A. B. C. D.
8.在锐角中,内角A,B,C的对边分别为a,b,c,已知,,则AB边上的高的取值范围为
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得2分,有选错的得0分。
9.已知m,n为两条不同的直线,,为两个不同的平面,下列命题正确的是
A. 若,,则
B. 若,,,,则
C. 若,,,则
D. 若,,,则
10.已知的内角A,B,C的对边分别为a,b,c,下列说法正确的是
A. 若,则
B. 若,,,则三角形有两解
C. 若的面积,则
D. 若,则为等腰三角形或直角三角形
11.如图1,某广场上放置了一些这样的石凳供大家休息,石凳是由正方体截去八个一样的正三棱锥得到的,它的所有边长均相同.如图2,设,则下列说法正确的是
A. 该多面体的表面积为
B. 过A,Q,G三点的平面截该多面体所得的截面面积为
C. 设O为平面AQG截该多面体所得截面多边形内一点包括边界,则的取值范围为
D. 该多面体外接球的体积为
三、填空题:本题共3小题,每小题5分,共15分。
12.已知向量,满足,,且,则 .
13.在中,角A,B,C的对边分别为a,b,c,已知,,,则 .
14.如图所示的正六边形ABCDEF,是由六个直角边长分别为与的全等的直角三角形拼接而成的,该图形阴影部分绕着线段AF的中垂线l旋转一周得到一个几何体,现在用密度为的材料去制造该几何体,则该几何体的质量为 结果用表示
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题13分
记的内角A,B,C的对边分别为a,b,c,已知
求角B;
若,,求的面积.
16.本小题15分
如图,在直四棱柱中,底面ABCD是矩形,,E,F分别是棱AD,BC的中点.
证明:平面
证明:平面平面
17.本小题15分
已知平面向量,将的起点放在坐标原点O处,然后将按逆时针方向旋转得到的向量为,设向量,
若,求实数t的值;
将向量与的起点放在O处,,,若与的夹角为,求的面积.
18.本小题17分
2025年4月19日,全球首个“人形机器人”半程马拉松在北京举行,某机构调查了1000名观众,将这1000名观众对“人形机器人”的评分数据分成,六组,得到如图所示的频率分布直方图.
求频率分布直方图中评分的中位数;
已知评分在这两区间内数据的方差分别为,,且每组以该组的中间值作为该组的平均值,现将评分在这两区间内的数据合在一起得到一组新的数据,求这组新数据的方差结果用分数表示
19.本小题17分
如图,在三棱锥中,由AB,AC,AD三条射线所构成的图形被称为“三面角”,设,,,设二面角的平面角为,则有
已知三棱锥的所有棱长均为1,求二面角的余弦值.
设直线AD与平面ABC所成的角为,证明
若,,,,,求点A到平面BCD的距离.
答案和解析
1.【答案】A
【解析】解:由复数的实部与虚部之和为0,
得,即
故选:
2.【答案】C
【解析】解:因为,所以为异面直线PB与CD所成的角.
因为平面ABCD,平面ABCD,所以
又,所以
故选:
3.【答案】B
【解析】解:如图,
故选:
4.【答案】D
【解析】解:对于A,因为5个数据从小到大排列为1,3,5,6,8,且,所以第60百分位数是,则A错误.
对于B,一组样本数据4,6,7,8,9,a的平均数为7,可知,解得,B错误.
对于C,因为在分层抽样中,每一层的抽样比是相同的,都等于总的抽样比,所以C错误.
对于D,因为的标准差为4,所以它的方差为16,
而的方差为,所以它的标准差是8,故D正确.
故选:
5.【答案】B
【解析】解:向量在向量上的投影向量为
故选:
6.【答案】D
【解析】解:对于A:太阳能发电装机容量占,超过,则扇形圆心角大于,所以A错误;
对于B:2024年我国火电发电装机容量占,因为,所以B错误;
对于C:2024年我国火电发电装机容量占,新能源太阳能、风电、核电的发电装机容量占比和为,所以C错误;
对于D:还要再建设的核电的发电装机容量为亿千瓦,所以D正确.
故选:
7.【答案】B
【解析】解:由题意可知在斜二测直观图中,,,
则,,,
由斜二测画法可得,在中,,,,
在三棱锥中,因为底面ABC,且,
所以可将三棱锥补成相邻的三条侧棱分别为6,4,8的长方体,
则三棱锥的外接球即为该长方体的外接球,
因为长方体的体对角线即为外接球的直径,
则外接球的半径,
故三棱锥外接球的表面积
故选:
8.【答案】C
【解析】解:因为是锐角三角形,所以,解得
由正弦定理可得,则,
设AB边上的高为h,由,
得,
所以
由,得,可得
所以
即AB边上的高的取值范围为
故选:
9.【答案】CD
【解析】解:对于A,若,,则或n与m异面,所以A错误.
对于B,若,,,,没有m,n是相交直线这个条件,不能得到,所以B错误.
对于C,由,得存在过直线m的平面与平面相交,令交线为c,则,而,,则,,因此,C正确.
对于D,若,,则,又,所以,D正确.
故选:
10.【答案】ACD
【解析】解:对于A,由可得,从而,A正确;
对于B,由正弦定理,得,
又因为,所以,所以B只有唯一解,B错误;
对于C,因为,
所以,又,解得,C正确;
对于D,因为,
由正弦定理得,即,
所以或,即或,
则为等腰三角形或直角三角形,D正确.
故选:
11.【答案】ABD
【解析】解:对于A,由,得正方体的棱长,
所以该多面体的表面积,A正确;
对于B,由平面的性质可知过A,Q,G三点的平面截该多面体所得的截面是边长为的正六边形ABGPQE,其面积为,B正确;
对于C,以A为坐标原点,建立如图所示的平面直角坐标系,
则,,设点,且,,
则,,
所以,即,C错误;
对于D,由多面体性质可知其外接球球心为该多面体的体心,
即正方体体心,设为为,
外接球的半径为,
所以该多面体外接球的体积为,D正确.
故选:
12.【答案】1
【解析】解:因为,所以,则,从而
故答案为:
13.【答案】
【解析】解:在中,由,可得
由正弦定理得即,可得
故答案为:
14.【答案】
【解析】解:外部正六边形的边长为,
旋转得到的几何体是两个全等的圆台,
上底面半径为,下底面半径为,高为,
体积为,
内部的六边形边长为2cm,旋转得到的几何体是一个圆柱和两个与圆柱同底的圆锥,
圆锥的底面半径为,高为1cm,圆柱的底面半径为,高为,
内部的六边形旋转得到的几何体的体积为,
所以该几何体的体积为,
用密度为的材料去制造该几何体,
则该几何体的质量为
故答案为:
15.【答案】解:因为,
所以,
因为,所以
又,所以
由,得,
解得负解舍
所以的面积为
【解析】详细解答和解析过程见【答案】
16.【答案】证明:因为E,F分别是矩形ABCD的棱AD,BC的中点,
所以,,
则四边形BEDF是平行四边形,从而,
又平面,平面,
所以平面;
证明:在矩形ABCD中,因为,E,F分别是棱AD,BC的中点,
所以,,,
所以,
从而,即,
因为四棱柱是直四棱柱,
所以平面ABCD,
又平面ABCD,所以,
因为,且平面,
所以平面
又平面,
所以平面平面
【解析】详细解答和解析过程见【答案】
17.【答案】解:根据三角函数的定义知,,
所以,则,
所以,
,
所以,解得
由知,,
由,得,
整理得,解得或
当时,,,
;
当时,,,
综上所述,的面积为或
【解析】详细解答和解析过程见【答案】
18.【答案】解:由图可知,前3个小矩形对应的频率之和为,所以中位数为70分.
对应的平均数为65分,对应的平均数为85分,
因为评分在这两组数据对应的频率为,
所以可以求出整体的平均数为分,
故所求评分的方差
【解析】详细解答和解析过程见【答案】
19.【答案】解:三棱锥的所有棱长均为1,
故,
由已知得;
证明:过点D作平面ABC的垂线,垂足为H,连接AH,则,
设,
在面ABC中,过点 H做于点T,连接DT,
因为平面ABC,平面ABC,所以,
又,平面DHT,
所以平面DHT,
因为平面DHT,所以,
故,又,,
即,
所以①,
在三面角中,同理可得②,
由①得,从而,
由②得,
所以
,
所以,
所以
;
在中,由,得,
故,
在中,由,得,
故,
在中,由,得,
所以,从而
设直线DA与平面BCD所成的角为,
由知,
所以,
则点A到平面BCD的距离为
【解析】详细解答和解析过程见【答案】
第2页,共2页
同课章节目录
