期末重组复习卷(二)(含解析)-高一数学下学期人教A版(2019)必修第二册
文档属性
| 名称 | 期末重组复习卷(二)(含解析)-高一数学下学期人教A版(2019)必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末重组复习卷(二)-高一数学下学期人教A版(2019)必修第二册
一.选择题(共8小题)
1.(2024秋 楚雄州期末)(2﹣3i)(3+i)的虚部为( )
A.9 B.﹣7 C.9i D.﹣7i
2.(2025春 凉州区校级期末)与向量平行的单位向量为( )
A.
B.
C.或
D.
3.(2025春 黄冈期末)如图所示为水平放置的正方形ABCO,在平面直角坐标系xOy中,点B的坐标为(2,2),用斜二测画法画出它的直观图A'B'C'O',则点B'到x'轴的距离为( )
A. B. C. D.
4.(2025春 龙潭区校级期末)已知m,n为两条不同的直线,α,β为两个不同的平面,则下列结论正确的是( )
A.若α∥β,m α,n β,则m∥n
B.若α⊥β,m α,n β,则m⊥n
C.若m∥α,α⊥β,则m⊥β
D.若m,n是异面直线,m α,n β;m∥β,n∥α,则α∥β
5.(2025春 宁夏校级期末)先后两次抛掷一枚质地均匀的正方体骰子,得到的点数分别为m,n,设平面向量,,则“”的概率为( )
A. B. C. D.
6.(2025春 天水校级期末)在△ABC中,A=60°,b=1,其面积为,则等于( )
A. B. C. D.
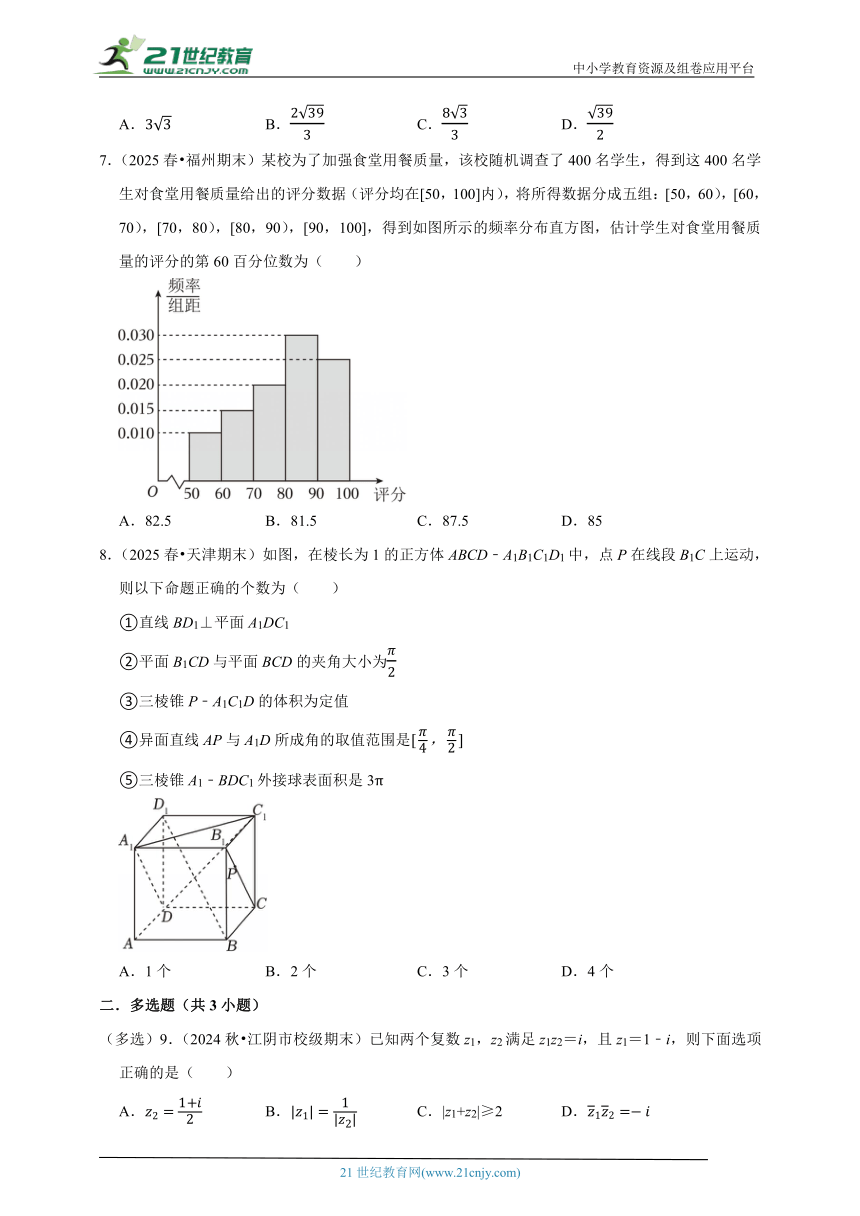
7.(2025春 福州期末)某校为了加强食堂用餐质量,该校随机调查了400名学生,得到这400名学生对食堂用餐质量给出的评分数据(评分均在[50,100]内),将所得数据分成五组:[50,60),[60,70),[70,80),[80,90),[90,100],得到如图所示的频率分布直方图,估计学生对食堂用餐质量的评分的第60百分位数为( )
A.82.5 B.81.5 C.87.5 D.85
8.(2025春 天津期末)如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,点P在线段B1C上运动,则以下命题正确的个数为( )
①直线BD1⊥平面A1DC1
②平面B1CD与平面BCD的夹角大小为
③三棱锥P﹣A1C1D的体积为定值
④异面直线AP与A1D所成角的取值范围是
⑤三棱锥A1﹣BDC1外接球表面积是3π
A.1个 B.2个 C.3个 D.4个
二.多选题(共3小题)
(多选)9.(2024秋 江阴市校级期末)已知两个复数z1,z2满足z1z2=i,且z1=1﹣i,则下面选项正确的是( )
A. B. C.|z1+z2|≥2 D.
(多选)10.(2025春 内江期末)抛掷两枚质地均匀的骰子,记“第一枚骰子出现的点数小于3”为事件A,“第二枚骰子出现的点数不小于3”为事件B,则下列结论中正确的是( )
A.事件A与事件B不互斥
B.事件A与事件B相互独立
C.P(B)=2P(A)
D.P(A)+P(B)<1
(多选)11.(2024秋 雁江区校级期末)如图,已知在棱长为2的正方体ABCD﹣A1B1C1D1中,点E,F,H分别是AB,DD1,BC1的中点,点G是A1D1上的动点,下列结论正确的是( )
A.C1D1∥平面ABH
B.AC1⊥平面BDA1
C.直线EF与BC1所成的角为30°
D.三棱锥G﹣DBC1的体积最大值为
三.填空题(共3小题)
12.(2024秋 海淀区期末)已知△ABC为等腰三角形,且sinA=2sinB,则cosB= .
13.(2025春 思茅区校级期末)已知点C为扇形AOB的弧AB上任意一点,且∠AOB=60°,若,则λ+μ的取值范围是 .
14.(2024秋 房县校级期末)如图所示,四边形A'B'C'D'是边长为2的正方形ABCD在平面α上的投影(光线AA'、BB'、CC'、DD'互相平行),光线AA'与平面α所成角为60°,转动正方形ABCD,在转动过程中保持BC∥平面α且BC⊥AA',若平面ABCD与平面α所成角为θ,且BB'=2cosθ,则多面体ABCD﹣A'B'C'D'的体积的最大值为 .
四.解答题(共5小题)
15.(2025春 内江期末)已知向量.
(1)求;
(2)若,求实数x的值.
16.(2025春 内江期末)某校组织高一年级学生进行了禁毒知识测试.根据测试成绩,将所得数据按照[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分成6组,其频率分布直方图如图所示.
(1)求a的值,并求该样本的第80百分位数;
(2)该校准备对本次禁毒知识测试成绩不及格(60分以下)的学生,采用按比例分配的分层随机抽样方法抽出5名同学,再从抽取的这5名同学中随机抽取2名同学进行情况了解,求这2名同学分数在[40,50),[50,60)各一人的概率.
17.(2025春 栖霞区校级期末)在△ABC中,a,b,c分别是角A,B,C的对边,且.
(1)求角B的大小;
(2)若a+c=2,S△ABC,求b的值.
18.(2025春 宁乡市期末)如图,四棱锥P﹣ABCD的侧面PAD是边长为2的正三角形,底面ABCD为正方形,且平面PAD⊥平面ABCD,M,N分别为AB,AD的中点.
(1)求四棱锥P﹣ABCD的体积;
(2)证明:DM⊥PC;
(3)求直线PM与平面PNC所成角的正弦值.
19.(2025春 河南校级期末)如图,在三棱柱ABC﹣A1B1C1中,A1A⊥底面ABC,且△ABC为正三角形,AA1=AB=6,D为AC的中点.
(1)求证:直线AB1∥平面BC1D;
(2)求证:平面BC1D⊥平面A1ACC1;
(3)求BC1与平面A1ACC1所成的角的正切值.
期末重组复习卷(二)-高一数学下学期人教A版(2019)必修第二册
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B C C D A B D C
二.多选题(共3小题)
题号 9 10 11
答案 BD ABC BCD
一.选择题(共8小题)
1.(2024秋 楚雄州期末)(2﹣3i)(3+i)的虚部为( )
A.9 B.﹣7 C.9i D.﹣7i
【解答】解:(2﹣3i)(3+i)=6﹣9i+2i﹣3i2=9﹣7i,
所以(2﹣3i)(3+i)的虚部为﹣7.
故选:B.
2.(2025春 凉州区校级期末)与向量平行的单位向量为( )
A.
B.
C.或
D.
【解答】解:由题意可知,,
所以与向量平行的单位向量为或.
故选:C.
3.(2025春 黄冈期末)如图所示为水平放置的正方形ABCO,在平面直角坐标系xOy中,点B的坐标为(2,2),用斜二测画法画出它的直观图A'B'C'O',则点B'到x'轴的距离为( )
A. B. C. D.
【解答】解:根据题意,由斜二测画法作出直观图,
其中B'C'=1,∠B'C'x'=45°,
则点B'到x'轴的距离d=1×sin45°.
故选:C.
4.(2025春 龙潭区校级期末)已知m,n为两条不同的直线,α,β为两个不同的平面,则下列结论正确的是( )
A.若α∥β,m α,n β,则m∥n
B.若α⊥β,m α,n β,则m⊥n
C.若m∥α,α⊥β,则m⊥β
D.若m,n是异面直线,m α,n β;m∥β,n∥α,则α∥β
【解答】解:对A选项,若α∥β,m α,n β,则m∥n或m与n异面,所以A选项错误.
对B选项,若α⊥β,m α,n β,则m与n可以成[0,]的任意角,所以B选项错误;
对于C,如图所示m∥α,α⊥β,但m∥β,所以C选项错误;
对于D选项,由n∥α,则过直线n作平面δ,使得δ∩α=l,于是n∥l,
而l β,n β,所以l∥β,由m,n是异面直线,则l,m必相交,
m∥β,l α,m α,所以α∥β,所以D选项正确.
故选:D.
5.(2025春 宁夏校级期末)先后两次抛掷一枚质地均匀的正方体骰子,得到的点数分别为m,n,设平面向量,,则“”的概率为( )
A. B. C. D.
【解答】解:因为,,所以0,
所以m>2n,由题意可知基本事件总数为6×6=36,
当n=1时,m=3,4,5,6,共四种情况;
当n=2时,m=5,6,共两种情况.
所以满足m>2n的基本事件个数为4+2=6,
因此,“”的概率.
故选:A.
6.(2025春 天水校级期末)在△ABC中,A=60°,b=1,其面积为,则等于( )
A. B. C. D.
【解答】解:在△ABC中,A=60°,b=1,其面积为,
则,
即c=4,
由余弦定理a2=b2+c2﹣2bccosA可得:a2=13,
即,
由正弦定理可得:,
故选:B.
7.(2025春 福州期末)某校为了加强食堂用餐质量,该校随机调查了400名学生,得到这400名学生对食堂用餐质量给出的评分数据(评分均在[50,100]内),将所得数据分成五组:[50,60),[60,70),[70,80),[80,90),[90,100],得到如图所示的频率分布直方图,估计学生对食堂用餐质量的评分的第60百分位数为( )
A.82.5 B.81.5 C.87.5 D.85
【解答】解:根据题意,设该组数据的第60百分位数为x,
第一组的频率为0.010×10=0.1,
第二组的频率为0.015×10=0.15,
第三组的频率为0.020×10=0.2,
第四组的频率为0.030×10=0.3,
则x在第四组,则有0.1+0.15+0.2+(x﹣80)×0.03=0.6,解可得x=85.
故生对食堂用餐质量的评分的第60百分位数为85.
故选:D.
8.(2025春 天津期末)如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,点P在线段B1C上运动,则以下命题正确的个数为( )
①直线BD1⊥平面A1DC1
②平面B1CD与平面BCD的夹角大小为
③三棱锥P﹣A1C1D的体积为定值
④异面直线AP与A1D所成角的取值范围是
⑤三棱锥A1﹣BDC1外接球表面积是3π
A.1个 B.2个 C.3个 D.4个
【解答】解:如图,连接B1D1,正方形A1B1C1D1中,A1C1⊥B1D1,
因为正方体的棱BB1⊥平面A1B1C1D1,A1C1 平面A1B1C1D1,
所以BB1⊥A1C1,
又因为BB1∩B1D1=B1,BB1,B1D1 平面BB1D1,
所以A1C1⊥平面BB1D1,
又BD1 平面BB1D1,所以A1C1⊥BD1,
同理A1D⊥BD1.
又A1D∩A1C1=A1,A1D,A1C1 平面A1C1D,
所以BD1⊥平面A1C1D,故①正确;
因为CD⊥平面BCB1,CB1 平面BCB1,所以CD⊥CB1,
又平面B1CD∩平面BCD=CD,BC⊥CD,BC 平面BCD,B1C 平面B1CD,
则∠B1CB是平面B1CD与平面BCD的夹角,因为△B1BC为等腰直角三角形,
所以该角大小为,故②错误;
因为A1B1∥AB,A1B1=AB,AB∥CD,AB=CD,
所以A1B1∥CD,A1B1=CD,
所以四边形A1B1CD为平行四边形,因此有A1D∥B1C,
又因为A1D 平面A1C1D,B1C 平面A1C1D,
所以B1C∥平面A1C1D,
又P∈B1C,所以P到平面A1C1D的距离为定值,
故三棱锥P﹣A1C1D的体积为定值,故③正确;
因为A1D∥B1C,所以异面直线AP与A1D所成角就是AP与B1C所成的角,
即图中∠APC或∠APB,设正方体棱长为1,
所以,
当点P为B1C中点时,此时AP⊥B1C,
因为△AB1C是等边三角形,P在线段B1C上,
所以∠APC或∠APB中较小的角的范围是,故④错误;
三棱锥A1﹣BDC1的外接球即为正方体ABCD﹣A1B1C1D1的外接球,
因为,
所以,
所以三棱锥A1﹣BDC1外接球表面积是πR2=3π,故⑤正确.
故选:C.
二.多选题(共3小题)
(多选)9.(2024秋 江阴市校级期末)已知两个复数z1,z2满足z1z2=i,且z1=1﹣i,则下面选项正确的是( )
A. B. C.|z1+z2|≥2 D.
【解答】解:两个复数z1,z2满足z1z2=i,且z1=1﹣i,
,故A错误;
对B:,∴,故B正确;
对C:,故,故C错误;
对D:,故D正确.
故选:BD.
(多选)10.(2025春 内江期末)抛掷两枚质地均匀的骰子,记“第一枚骰子出现的点数小于3”为事件A,“第二枚骰子出现的点数不小于3”为事件B,则下列结论中正确的是( )
A.事件A与事件B不互斥
B.事件A与事件B相互独立
C.P(B)=2P(A)
D.P(A)+P(B)<1
【解答】解:根据题意,抛掷两枚质地均匀的骰子,
则Ω={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)},共36个基本事件,
依次分析选项:
对于A,事件AB={(1,3),(1,4),(1,5),(1,6),
(2,3),(2,4),(2,5),(2,6),},共8个基本事件,
事件A、B可同时发生,即事件A与事件B不互斥,A正确;
对于B,易得,
则有,即事件A与事件B相互独立,B正确;
显然,,C正确,D错误.
故选:ABC.
(多选)11.(2024秋 雁江区校级期末)如图,已知在棱长为2的正方体ABCD﹣A1B1C1D1中,点E,F,H分别是AB,DD1,BC1的中点,点G是A1D1上的动点,下列结论正确的是( )
A.C1D1∥平面ABH
B.AC1⊥平面BDA1
C.直线EF与BC1所成的角为30°
D.三棱锥G﹣DBC1的体积最大值为
【解答】解:如图:
因为AB∥C1D1,所以A,B,C1,D1四点共面,
所以C1D1 平面ABH,所以A选项错误;
连接BD,AC,AB1,A1B,AC1,
根据三垂线定理易知A1B⊥AC1,又AC1⊥BD,又A1B∩BD=B,
所以AC1⊥面BDA1,所以B选项正确;
取AD中点I,连接FI,EF,EI,AD1,
在△ADD1中,因为F,I分别为DD1,DA的中点,
所以FI∥AD1,又AD1∥BC1,
所以FI∥BC1,
所以EF与BC1所成角为∠IFE,
又,,,
所以,
所以EF与BC1所成的角为30°,所以C选项正确;
当G位于A1点时,三棱锥G﹣DBC1的体积最大,
所以,所以选项D正确.
故选:BCD.
三.填空题(共3小题)
12.(2024秋 海淀区期末)已知△ABC为等腰三角形,且sinA=2sinB,则cosB= .
【解答】解:设△ABC三个内角A,B,C所对的边分别为a,b,c,
因为sinA=2sinB,则由正弦定理得a=2b,
因为△ABC是等腰三角形,所以a=c=2b,
由余弦定理得:.
故答案为:.
13.(2025春 思茅区校级期末)已知点C为扇形AOB的弧AB上任意一点,且∠AOB=60°,若,则λ+μ的取值范围是 .
【解答】解:设λ+μ=k,如图,当C位于点A或点B时,A,B,C三点共线,所以k=λ+μ=1;
当点C运动到AB的中点时,,所以.
故答案为:.
14.(2024秋 房县校级期末)如图所示,四边形A'B'C'D'是边长为2的正方形ABCD在平面α上的投影(光线AA'、BB'、CC'、DD'互相平行),光线AA'与平面α所成角为60°,转动正方形ABCD,在转动过程中保持BC∥平面α且BC⊥AA',若平面ABCD与平面α所成角为θ,且BB'=2cosθ,则多面体ABCD﹣A'B'C'D'的体积的最大值为 .
【解答】解:因为BC⊥AA',BC⊥AB,AB∩AA'=A,
所以BC⊥平面ABB'A',
因为BC∥α,BC 平面BCC'B',且平面BCC'B'∩α=B'C',
所以BC∥B'C',又BB'∥CC',
所以四边形BCC'B'为平行四边形,
所以BC=B′C′,同理可得AD=A′D′,又AD=BC
所以多面体ABCD﹣A'B'C'D'为直四棱柱,
作BM∥A'B'交AA'于点M,A'B' 平面A'B'C'D',
所以BM∥平面A'B'C'D';
同理BC∥平面A'B'C'D',又BC∩BM=B,
所以平面BCM∥平面A'B'C'D',
又BC⊥平面ABB'A',
所以∠ABM=θ;
作AN⊥A'B'于N,
所以BC⊥AN,即B'C'⊥AN,又A'B'∩B'C'=B',所以AN⊥平面A'B'C'D',
所以直线AA'与平面α所成角为∠AA'N=60°,
所以∠AMB=∠AA'N=60°;
在△ABM中,由正弦定理得,,
点B到直线AA'的距离为,
所以多面体ABCD﹣A'B'C'D'的体积
,
化简得,当且仅当时取等.
故答案为:.
四.解答题(共5小题)
15.(2025春 内江期末)已知向量.
(1)求;
(2)若,求实数x的值.
【解答】解:(1)因为,
所以;
(2)由题可得:,,
已知,可得,
即(﹣5)×1+(2+x)×5=0,
整理得:5x+5=0,解得:x=﹣1.
16.(2025春 内江期末)某校组织高一年级学生进行了禁毒知识测试.根据测试成绩,将所得数据按照[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分成6组,其频率分布直方图如图所示.
(1)求a的值,并求该样本的第80百分位数;
(2)该校准备对本次禁毒知识测试成绩不及格(60分以下)的学生,采用按比例分配的分层随机抽样方法抽出5名同学,再从抽取的这5名同学中随机抽取2名同学进行情况了解,求这2名同学分数在[40,50),[50,60)各一人的概率.
【解答】解:(1)(0.01+0.015+0.015+a+0.025+0.005)×10=1,a=0.030,
由(0.01+0.015+0.015+0.03)×10=0.7<0.8,(0.07+0.025)×10=0.95>0.8,
因此样本的第80百分位数位于区间[80,90),设为x,则0.7+(x﹣80)×0.025=0.8,
因此x=84分;
(2)[40,50),[50,60)的频率比为2:3,
故抽取的5人中[40,50)有2人为a,b、[50,60)有3人为A,B,C,
任抽2人有{ab,aA,aB,aC,bA,bB,bC,AB,AC,BC},共10种情况,
其中分数在[40,50),[50,60)各一人有{aA,aB,aC,bA,bB,bC},共6种情况,
因此这2名同学分数在[40,50),[50,60)各一人的概率.
17.(2025春 栖霞区校级期末)在△ABC中,a,b,c分别是角A,B,C的对边,且.
(1)求角B的大小;
(2)若a+c=2,S△ABC,求b的值.
【解答】解:(1)在△ABC中,∵,由正弦定理可得:.
化为:2sinAcosB+sinCcosB+cosCsinB=0,
2sinAcosB+sin(C+B)=0,
∴2sinAcosB+sinA=0,
∵sinA≠0,
∴cosB,又B∈(0,π),∴B.
(2)∵,
∴ac=1.
∴b2=a2+c2﹣2accosB=a2+c2+ac=(a+c)2﹣ac=3,
∴.
18.(2025春 宁乡市期末)如图,四棱锥P﹣ABCD的侧面PAD是边长为2的正三角形,底面ABCD为正方形,且平面PAD⊥平面ABCD,M,N分别为AB,AD的中点.
(1)求四棱锥P﹣ABCD的体积;
(2)证明:DM⊥PC;
(3)求直线PM与平面PNC所成角的正弦值.
【解答】解:(1)因为侧面PAD是边长为2的正三角形,N为AD的中点,
因此PN⊥AD,,
因为平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,PN 平面PAD,
因此PN⊥平面ABCD,即PN为棱锥的高,
因为底面ABCD为正方形,
因此四棱锥P﹣ABCD的体积为;
(2)证明:因为DM 平面ABCD,PN⊥平面ABCD,因此PN⊥DM,
在正方形ABCD中,易知△DAM与△CDN全等,
因此∠ADM+∠AMD=∠ADM+∠CND=90°,因此DM⊥CN,
又PN∩CN=N,PN,CN 平面PNC,因此DM⊥平面PNC,
又PC 平面PNC,因此DM⊥PC;
(3)
设CN∩DM=E,连接PE,PM,MN,
因为DM⊥平面PNC,
因此∠MPE为直线PM与平面PNC所成的角,
在Rt△CDN中,,又,
即,因此,
又在Rt△PNM中,,
因此.
19.(2025春 河南校级期末)如图,在三棱柱ABC﹣A1B1C1中,A1A⊥底面ABC,且△ABC为正三角形,AA1=AB=6,D为AC的中点.
(1)求证:直线AB1∥平面BC1D;
(2)求证:平面BC1D⊥平面A1ACC1;
(3)求BC1与平面A1ACC1所成的角的正切值.
【解答】解:(1)证明;设B1C∩C1B=O,连接DO,
因为在三棱柱ABC﹣A1B1C1中,A1A⊥底面ABC,且△ABC为正三角形,
所以三棱柱ABC﹣A1B1C1为正三棱柱,侧面C1CBB1为正方形,
所以O为B1C的中点,又∵D为AC的中点,
所以在△ACB1中有DO∥AB1,
因为AB1 平面BC1D,DO 平面BC1D,
所以AB1∥平面BC1D;
(2)连接BD,
因为A1A⊥底面ABC,BD 平面ABC,所以A1A⊥BD,
又因为△ABC为正三角形,D为AC的中点,所以AC⊥BD,
又因为A1A∩AC=A,又因为A1A 平面A1ACC1,AC 平面A1ACC1,
所以BD⊥平面A1ACC1,又因为BD 平面BC1D,
所以平面BC1D⊥平面A1ACC1;
(3)由(2)可知BD⊥平面A1ACC1,
所以DC1即为BC1在平面A1ACC1内的射影,
所以∠BC1D即为BC1与平面A1ACC1所成的角,
因为三棱柱ABC﹣A1B1C1为正三棱柱,且AA1=AB=6,
所以,,
所以.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末重组复习卷(二)-高一数学下学期人教A版(2019)必修第二册
一.选择题(共8小题)
1.(2024秋 楚雄州期末)(2﹣3i)(3+i)的虚部为( )
A.9 B.﹣7 C.9i D.﹣7i
2.(2025春 凉州区校级期末)与向量平行的单位向量为( )
A.
B.
C.或
D.
3.(2025春 黄冈期末)如图所示为水平放置的正方形ABCO,在平面直角坐标系xOy中,点B的坐标为(2,2),用斜二测画法画出它的直观图A'B'C'O',则点B'到x'轴的距离为( )
A. B. C. D.
4.(2025春 龙潭区校级期末)已知m,n为两条不同的直线,α,β为两个不同的平面,则下列结论正确的是( )
A.若α∥β,m α,n β,则m∥n
B.若α⊥β,m α,n β,则m⊥n
C.若m∥α,α⊥β,则m⊥β
D.若m,n是异面直线,m α,n β;m∥β,n∥α,则α∥β
5.(2025春 宁夏校级期末)先后两次抛掷一枚质地均匀的正方体骰子,得到的点数分别为m,n,设平面向量,,则“”的概率为( )
A. B. C. D.
6.(2025春 天水校级期末)在△ABC中,A=60°,b=1,其面积为,则等于( )
A. B. C. D.
7.(2025春 福州期末)某校为了加强食堂用餐质量,该校随机调查了400名学生,得到这400名学生对食堂用餐质量给出的评分数据(评分均在[50,100]内),将所得数据分成五组:[50,60),[60,70),[70,80),[80,90),[90,100],得到如图所示的频率分布直方图,估计学生对食堂用餐质量的评分的第60百分位数为( )
A.82.5 B.81.5 C.87.5 D.85
8.(2025春 天津期末)如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,点P在线段B1C上运动,则以下命题正确的个数为( )
①直线BD1⊥平面A1DC1
②平面B1CD与平面BCD的夹角大小为
③三棱锥P﹣A1C1D的体积为定值
④异面直线AP与A1D所成角的取值范围是
⑤三棱锥A1﹣BDC1外接球表面积是3π
A.1个 B.2个 C.3个 D.4个
二.多选题(共3小题)
(多选)9.(2024秋 江阴市校级期末)已知两个复数z1,z2满足z1z2=i,且z1=1﹣i,则下面选项正确的是( )
A. B. C.|z1+z2|≥2 D.
(多选)10.(2025春 内江期末)抛掷两枚质地均匀的骰子,记“第一枚骰子出现的点数小于3”为事件A,“第二枚骰子出现的点数不小于3”为事件B,则下列结论中正确的是( )
A.事件A与事件B不互斥
B.事件A与事件B相互独立
C.P(B)=2P(A)
D.P(A)+P(B)<1
(多选)11.(2024秋 雁江区校级期末)如图,已知在棱长为2的正方体ABCD﹣A1B1C1D1中,点E,F,H分别是AB,DD1,BC1的中点,点G是A1D1上的动点,下列结论正确的是( )
A.C1D1∥平面ABH
B.AC1⊥平面BDA1
C.直线EF与BC1所成的角为30°
D.三棱锥G﹣DBC1的体积最大值为
三.填空题(共3小题)
12.(2024秋 海淀区期末)已知△ABC为等腰三角形,且sinA=2sinB,则cosB= .
13.(2025春 思茅区校级期末)已知点C为扇形AOB的弧AB上任意一点,且∠AOB=60°,若,则λ+μ的取值范围是 .
14.(2024秋 房县校级期末)如图所示,四边形A'B'C'D'是边长为2的正方形ABCD在平面α上的投影(光线AA'、BB'、CC'、DD'互相平行),光线AA'与平面α所成角为60°,转动正方形ABCD,在转动过程中保持BC∥平面α且BC⊥AA',若平面ABCD与平面α所成角为θ,且BB'=2cosθ,则多面体ABCD﹣A'B'C'D'的体积的最大值为 .
四.解答题(共5小题)
15.(2025春 内江期末)已知向量.
(1)求;
(2)若,求实数x的值.
16.(2025春 内江期末)某校组织高一年级学生进行了禁毒知识测试.根据测试成绩,将所得数据按照[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分成6组,其频率分布直方图如图所示.
(1)求a的值,并求该样本的第80百分位数;
(2)该校准备对本次禁毒知识测试成绩不及格(60分以下)的学生,采用按比例分配的分层随机抽样方法抽出5名同学,再从抽取的这5名同学中随机抽取2名同学进行情况了解,求这2名同学分数在[40,50),[50,60)各一人的概率.
17.(2025春 栖霞区校级期末)在△ABC中,a,b,c分别是角A,B,C的对边,且.
(1)求角B的大小;
(2)若a+c=2,S△ABC,求b的值.
18.(2025春 宁乡市期末)如图,四棱锥P﹣ABCD的侧面PAD是边长为2的正三角形,底面ABCD为正方形,且平面PAD⊥平面ABCD,M,N分别为AB,AD的中点.
(1)求四棱锥P﹣ABCD的体积;
(2)证明:DM⊥PC;
(3)求直线PM与平面PNC所成角的正弦值.
19.(2025春 河南校级期末)如图,在三棱柱ABC﹣A1B1C1中,A1A⊥底面ABC,且△ABC为正三角形,AA1=AB=6,D为AC的中点.
(1)求证:直线AB1∥平面BC1D;
(2)求证:平面BC1D⊥平面A1ACC1;
(3)求BC1与平面A1ACC1所成的角的正切值.
期末重组复习卷(二)-高一数学下学期人教A版(2019)必修第二册
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B C C D A B D C
二.多选题(共3小题)
题号 9 10 11
答案 BD ABC BCD
一.选择题(共8小题)
1.(2024秋 楚雄州期末)(2﹣3i)(3+i)的虚部为( )
A.9 B.﹣7 C.9i D.﹣7i
【解答】解:(2﹣3i)(3+i)=6﹣9i+2i﹣3i2=9﹣7i,
所以(2﹣3i)(3+i)的虚部为﹣7.
故选:B.
2.(2025春 凉州区校级期末)与向量平行的单位向量为( )
A.
B.
C.或
D.
【解答】解:由题意可知,,
所以与向量平行的单位向量为或.
故选:C.
3.(2025春 黄冈期末)如图所示为水平放置的正方形ABCO,在平面直角坐标系xOy中,点B的坐标为(2,2),用斜二测画法画出它的直观图A'B'C'O',则点B'到x'轴的距离为( )
A. B. C. D.
【解答】解:根据题意,由斜二测画法作出直观图,
其中B'C'=1,∠B'C'x'=45°,
则点B'到x'轴的距离d=1×sin45°.
故选:C.
4.(2025春 龙潭区校级期末)已知m,n为两条不同的直线,α,β为两个不同的平面,则下列结论正确的是( )
A.若α∥β,m α,n β,则m∥n
B.若α⊥β,m α,n β,则m⊥n
C.若m∥α,α⊥β,则m⊥β
D.若m,n是异面直线,m α,n β;m∥β,n∥α,则α∥β
【解答】解:对A选项,若α∥β,m α,n β,则m∥n或m与n异面,所以A选项错误.
对B选项,若α⊥β,m α,n β,则m与n可以成[0,]的任意角,所以B选项错误;
对于C,如图所示m∥α,α⊥β,但m∥β,所以C选项错误;
对于D选项,由n∥α,则过直线n作平面δ,使得δ∩α=l,于是n∥l,
而l β,n β,所以l∥β,由m,n是异面直线,则l,m必相交,
m∥β,l α,m α,所以α∥β,所以D选项正确.
故选:D.
5.(2025春 宁夏校级期末)先后两次抛掷一枚质地均匀的正方体骰子,得到的点数分别为m,n,设平面向量,,则“”的概率为( )
A. B. C. D.
【解答】解:因为,,所以0,
所以m>2n,由题意可知基本事件总数为6×6=36,
当n=1时,m=3,4,5,6,共四种情况;
当n=2时,m=5,6,共两种情况.
所以满足m>2n的基本事件个数为4+2=6,
因此,“”的概率.
故选:A.
6.(2025春 天水校级期末)在△ABC中,A=60°,b=1,其面积为,则等于( )
A. B. C. D.
【解答】解:在△ABC中,A=60°,b=1,其面积为,
则,
即c=4,
由余弦定理a2=b2+c2﹣2bccosA可得:a2=13,
即,
由正弦定理可得:,
故选:B.
7.(2025春 福州期末)某校为了加强食堂用餐质量,该校随机调查了400名学生,得到这400名学生对食堂用餐质量给出的评分数据(评分均在[50,100]内),将所得数据分成五组:[50,60),[60,70),[70,80),[80,90),[90,100],得到如图所示的频率分布直方图,估计学生对食堂用餐质量的评分的第60百分位数为( )
A.82.5 B.81.5 C.87.5 D.85
【解答】解:根据题意,设该组数据的第60百分位数为x,
第一组的频率为0.010×10=0.1,
第二组的频率为0.015×10=0.15,
第三组的频率为0.020×10=0.2,
第四组的频率为0.030×10=0.3,
则x在第四组,则有0.1+0.15+0.2+(x﹣80)×0.03=0.6,解可得x=85.
故生对食堂用餐质量的评分的第60百分位数为85.
故选:D.
8.(2025春 天津期末)如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,点P在线段B1C上运动,则以下命题正确的个数为( )
①直线BD1⊥平面A1DC1
②平面B1CD与平面BCD的夹角大小为
③三棱锥P﹣A1C1D的体积为定值
④异面直线AP与A1D所成角的取值范围是
⑤三棱锥A1﹣BDC1外接球表面积是3π
A.1个 B.2个 C.3个 D.4个
【解答】解:如图,连接B1D1,正方形A1B1C1D1中,A1C1⊥B1D1,
因为正方体的棱BB1⊥平面A1B1C1D1,A1C1 平面A1B1C1D1,
所以BB1⊥A1C1,
又因为BB1∩B1D1=B1,BB1,B1D1 平面BB1D1,
所以A1C1⊥平面BB1D1,
又BD1 平面BB1D1,所以A1C1⊥BD1,
同理A1D⊥BD1.
又A1D∩A1C1=A1,A1D,A1C1 平面A1C1D,
所以BD1⊥平面A1C1D,故①正确;
因为CD⊥平面BCB1,CB1 平面BCB1,所以CD⊥CB1,
又平面B1CD∩平面BCD=CD,BC⊥CD,BC 平面BCD,B1C 平面B1CD,
则∠B1CB是平面B1CD与平面BCD的夹角,因为△B1BC为等腰直角三角形,
所以该角大小为,故②错误;
因为A1B1∥AB,A1B1=AB,AB∥CD,AB=CD,
所以A1B1∥CD,A1B1=CD,
所以四边形A1B1CD为平行四边形,因此有A1D∥B1C,
又因为A1D 平面A1C1D,B1C 平面A1C1D,
所以B1C∥平面A1C1D,
又P∈B1C,所以P到平面A1C1D的距离为定值,
故三棱锥P﹣A1C1D的体积为定值,故③正确;
因为A1D∥B1C,所以异面直线AP与A1D所成角就是AP与B1C所成的角,
即图中∠APC或∠APB,设正方体棱长为1,
所以,
当点P为B1C中点时,此时AP⊥B1C,
因为△AB1C是等边三角形,P在线段B1C上,
所以∠APC或∠APB中较小的角的范围是,故④错误;
三棱锥A1﹣BDC1的外接球即为正方体ABCD﹣A1B1C1D1的外接球,
因为,
所以,
所以三棱锥A1﹣BDC1外接球表面积是πR2=3π,故⑤正确.
故选:C.
二.多选题(共3小题)
(多选)9.(2024秋 江阴市校级期末)已知两个复数z1,z2满足z1z2=i,且z1=1﹣i,则下面选项正确的是( )
A. B. C.|z1+z2|≥2 D.
【解答】解:两个复数z1,z2满足z1z2=i,且z1=1﹣i,
,故A错误;
对B:,∴,故B正确;
对C:,故,故C错误;
对D:,故D正确.
故选:BD.
(多选)10.(2025春 内江期末)抛掷两枚质地均匀的骰子,记“第一枚骰子出现的点数小于3”为事件A,“第二枚骰子出现的点数不小于3”为事件B,则下列结论中正确的是( )
A.事件A与事件B不互斥
B.事件A与事件B相互独立
C.P(B)=2P(A)
D.P(A)+P(B)<1
【解答】解:根据题意,抛掷两枚质地均匀的骰子,
则Ω={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)},共36个基本事件,
依次分析选项:
对于A,事件AB={(1,3),(1,4),(1,5),(1,6),
(2,3),(2,4),(2,5),(2,6),},共8个基本事件,
事件A、B可同时发生,即事件A与事件B不互斥,A正确;
对于B,易得,
则有,即事件A与事件B相互独立,B正确;
显然,,C正确,D错误.
故选:ABC.
(多选)11.(2024秋 雁江区校级期末)如图,已知在棱长为2的正方体ABCD﹣A1B1C1D1中,点E,F,H分别是AB,DD1,BC1的中点,点G是A1D1上的动点,下列结论正确的是( )
A.C1D1∥平面ABH
B.AC1⊥平面BDA1
C.直线EF与BC1所成的角为30°
D.三棱锥G﹣DBC1的体积最大值为
【解答】解:如图:
因为AB∥C1D1,所以A,B,C1,D1四点共面,
所以C1D1 平面ABH,所以A选项错误;
连接BD,AC,AB1,A1B,AC1,
根据三垂线定理易知A1B⊥AC1,又AC1⊥BD,又A1B∩BD=B,
所以AC1⊥面BDA1,所以B选项正确;
取AD中点I,连接FI,EF,EI,AD1,
在△ADD1中,因为F,I分别为DD1,DA的中点,
所以FI∥AD1,又AD1∥BC1,
所以FI∥BC1,
所以EF与BC1所成角为∠IFE,
又,,,
所以,
所以EF与BC1所成的角为30°,所以C选项正确;
当G位于A1点时,三棱锥G﹣DBC1的体积最大,
所以,所以选项D正确.
故选:BCD.
三.填空题(共3小题)
12.(2024秋 海淀区期末)已知△ABC为等腰三角形,且sinA=2sinB,则cosB= .
【解答】解:设△ABC三个内角A,B,C所对的边分别为a,b,c,
因为sinA=2sinB,则由正弦定理得a=2b,
因为△ABC是等腰三角形,所以a=c=2b,
由余弦定理得:.
故答案为:.
13.(2025春 思茅区校级期末)已知点C为扇形AOB的弧AB上任意一点,且∠AOB=60°,若,则λ+μ的取值范围是 .
【解答】解:设λ+μ=k,如图,当C位于点A或点B时,A,B,C三点共线,所以k=λ+μ=1;
当点C运动到AB的中点时,,所以.
故答案为:.
14.(2024秋 房县校级期末)如图所示,四边形A'B'C'D'是边长为2的正方形ABCD在平面α上的投影(光线AA'、BB'、CC'、DD'互相平行),光线AA'与平面α所成角为60°,转动正方形ABCD,在转动过程中保持BC∥平面α且BC⊥AA',若平面ABCD与平面α所成角为θ,且BB'=2cosθ,则多面体ABCD﹣A'B'C'D'的体积的最大值为 .
【解答】解:因为BC⊥AA',BC⊥AB,AB∩AA'=A,
所以BC⊥平面ABB'A',
因为BC∥α,BC 平面BCC'B',且平面BCC'B'∩α=B'C',
所以BC∥B'C',又BB'∥CC',
所以四边形BCC'B'为平行四边形,
所以BC=B′C′,同理可得AD=A′D′,又AD=BC
所以多面体ABCD﹣A'B'C'D'为直四棱柱,
作BM∥A'B'交AA'于点M,A'B' 平面A'B'C'D',
所以BM∥平面A'B'C'D';
同理BC∥平面A'B'C'D',又BC∩BM=B,
所以平面BCM∥平面A'B'C'D',
又BC⊥平面ABB'A',
所以∠ABM=θ;
作AN⊥A'B'于N,
所以BC⊥AN,即B'C'⊥AN,又A'B'∩B'C'=B',所以AN⊥平面A'B'C'D',
所以直线AA'与平面α所成角为∠AA'N=60°,
所以∠AMB=∠AA'N=60°;
在△ABM中,由正弦定理得,,
点B到直线AA'的距离为,
所以多面体ABCD﹣A'B'C'D'的体积
,
化简得,当且仅当时取等.
故答案为:.
四.解答题(共5小题)
15.(2025春 内江期末)已知向量.
(1)求;
(2)若,求实数x的值.
【解答】解:(1)因为,
所以;
(2)由题可得:,,
已知,可得,
即(﹣5)×1+(2+x)×5=0,
整理得:5x+5=0,解得:x=﹣1.
16.(2025春 内江期末)某校组织高一年级学生进行了禁毒知识测试.根据测试成绩,将所得数据按照[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]分成6组,其频率分布直方图如图所示.
(1)求a的值,并求该样本的第80百分位数;
(2)该校准备对本次禁毒知识测试成绩不及格(60分以下)的学生,采用按比例分配的分层随机抽样方法抽出5名同学,再从抽取的这5名同学中随机抽取2名同学进行情况了解,求这2名同学分数在[40,50),[50,60)各一人的概率.
【解答】解:(1)(0.01+0.015+0.015+a+0.025+0.005)×10=1,a=0.030,
由(0.01+0.015+0.015+0.03)×10=0.7<0.8,(0.07+0.025)×10=0.95>0.8,
因此样本的第80百分位数位于区间[80,90),设为x,则0.7+(x﹣80)×0.025=0.8,
因此x=84分;
(2)[40,50),[50,60)的频率比为2:3,
故抽取的5人中[40,50)有2人为a,b、[50,60)有3人为A,B,C,
任抽2人有{ab,aA,aB,aC,bA,bB,bC,AB,AC,BC},共10种情况,
其中分数在[40,50),[50,60)各一人有{aA,aB,aC,bA,bB,bC},共6种情况,
因此这2名同学分数在[40,50),[50,60)各一人的概率.
17.(2025春 栖霞区校级期末)在△ABC中,a,b,c分别是角A,B,C的对边,且.
(1)求角B的大小;
(2)若a+c=2,S△ABC,求b的值.
【解答】解:(1)在△ABC中,∵,由正弦定理可得:.
化为:2sinAcosB+sinCcosB+cosCsinB=0,
2sinAcosB+sin(C+B)=0,
∴2sinAcosB+sinA=0,
∵sinA≠0,
∴cosB,又B∈(0,π),∴B.
(2)∵,
∴ac=1.
∴b2=a2+c2﹣2accosB=a2+c2+ac=(a+c)2﹣ac=3,
∴.
18.(2025春 宁乡市期末)如图,四棱锥P﹣ABCD的侧面PAD是边长为2的正三角形,底面ABCD为正方形,且平面PAD⊥平面ABCD,M,N分别为AB,AD的中点.
(1)求四棱锥P﹣ABCD的体积;
(2)证明:DM⊥PC;
(3)求直线PM与平面PNC所成角的正弦值.
【解答】解:(1)因为侧面PAD是边长为2的正三角形,N为AD的中点,
因此PN⊥AD,,
因为平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,PN 平面PAD,
因此PN⊥平面ABCD,即PN为棱锥的高,
因为底面ABCD为正方形,
因此四棱锥P﹣ABCD的体积为;
(2)证明:因为DM 平面ABCD,PN⊥平面ABCD,因此PN⊥DM,
在正方形ABCD中,易知△DAM与△CDN全等,
因此∠ADM+∠AMD=∠ADM+∠CND=90°,因此DM⊥CN,
又PN∩CN=N,PN,CN 平面PNC,因此DM⊥平面PNC,
又PC 平面PNC,因此DM⊥PC;
(3)
设CN∩DM=E,连接PE,PM,MN,
因为DM⊥平面PNC,
因此∠MPE为直线PM与平面PNC所成的角,
在Rt△CDN中,,又,
即,因此,
又在Rt△PNM中,,
因此.
19.(2025春 河南校级期末)如图,在三棱柱ABC﹣A1B1C1中,A1A⊥底面ABC,且△ABC为正三角形,AA1=AB=6,D为AC的中点.
(1)求证:直线AB1∥平面BC1D;
(2)求证:平面BC1D⊥平面A1ACC1;
(3)求BC1与平面A1ACC1所成的角的正切值.
【解答】解:(1)证明;设B1C∩C1B=O,连接DO,
因为在三棱柱ABC﹣A1B1C1中,A1A⊥底面ABC,且△ABC为正三角形,
所以三棱柱ABC﹣A1B1C1为正三棱柱,侧面C1CBB1为正方形,
所以O为B1C的中点,又∵D为AC的中点,
所以在△ACB1中有DO∥AB1,
因为AB1 平面BC1D,DO 平面BC1D,
所以AB1∥平面BC1D;
(2)连接BD,
因为A1A⊥底面ABC,BD 平面ABC,所以A1A⊥BD,
又因为△ABC为正三角形,D为AC的中点,所以AC⊥BD,
又因为A1A∩AC=A,又因为A1A 平面A1ACC1,AC 平面A1ACC1,
所以BD⊥平面A1ACC1,又因为BD 平面BC1D,
所以平面BC1D⊥平面A1ACC1;
(3)由(2)可知BD⊥平面A1ACC1,
所以DC1即为BC1在平面A1ACC1内的射影,
所以∠BC1D即为BC1与平面A1ACC1所成的角,
因为三棱柱ABC﹣A1B1C1为正三棱柱,且AA1=AB=6,
所以,,
所以.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
