10.1相交线 教案 沪科版(2024)数学七年级下册
文档属性
| 名称 | 10.1相交线 教案 沪科版(2024)数学七年级下册 |

|
|
| 格式 | doc | ||
| 文件大小 | 144.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 16:28:59 | ||
图片预览

文档简介
《10.1.1相交线》教学设计
教学目标:
在具体生活情境中感受两条直线相交的情形,进一步体会对顶角、邻补角等概念的形成过程.
准确理解对顶角、邻补角的概念,并能在具体图形中熟练辨认对顶角、邻补角.
3、理解对顶角、邻补角的数量关系,并能进行相关简单计算.
教学重难点:
重点: 对顶角、邻补角的概念,对顶角的性质.
难点:对顶角性质的理解与应用.
教学过程:
一.创设情境 导入新课
1、课件展示剪刀图片,让学生观察、感受剪刀中的相交线,从而引出课题,并介绍相交线及相关的概念.
2、结合你的生活,你能在身边再找出一些相交线的实例吗
让学生进一步在具体生活情景中感受两条直线相交的情形.
二、探究对顶角、邻补角的概念
思考:两条直线相交,形成的小于平角的角有几个?将这些角两两配对组合,共能组成几对角?根据这种位置关系将它们分类,能分几类?
学生分组讨论在具体图形中得出的两条相交线构成的四个角,根据图形分类,然后描述对顶角、邻补角的特征.
师生共同归纳得出对顶角、邻补角的概念.
对顶角的概念:有公共顶点,两边互为反向延长线.
邻补角的概念:有公共顶点,其中一边为公共边,另一边互为反向延长线.
小试牛刀:
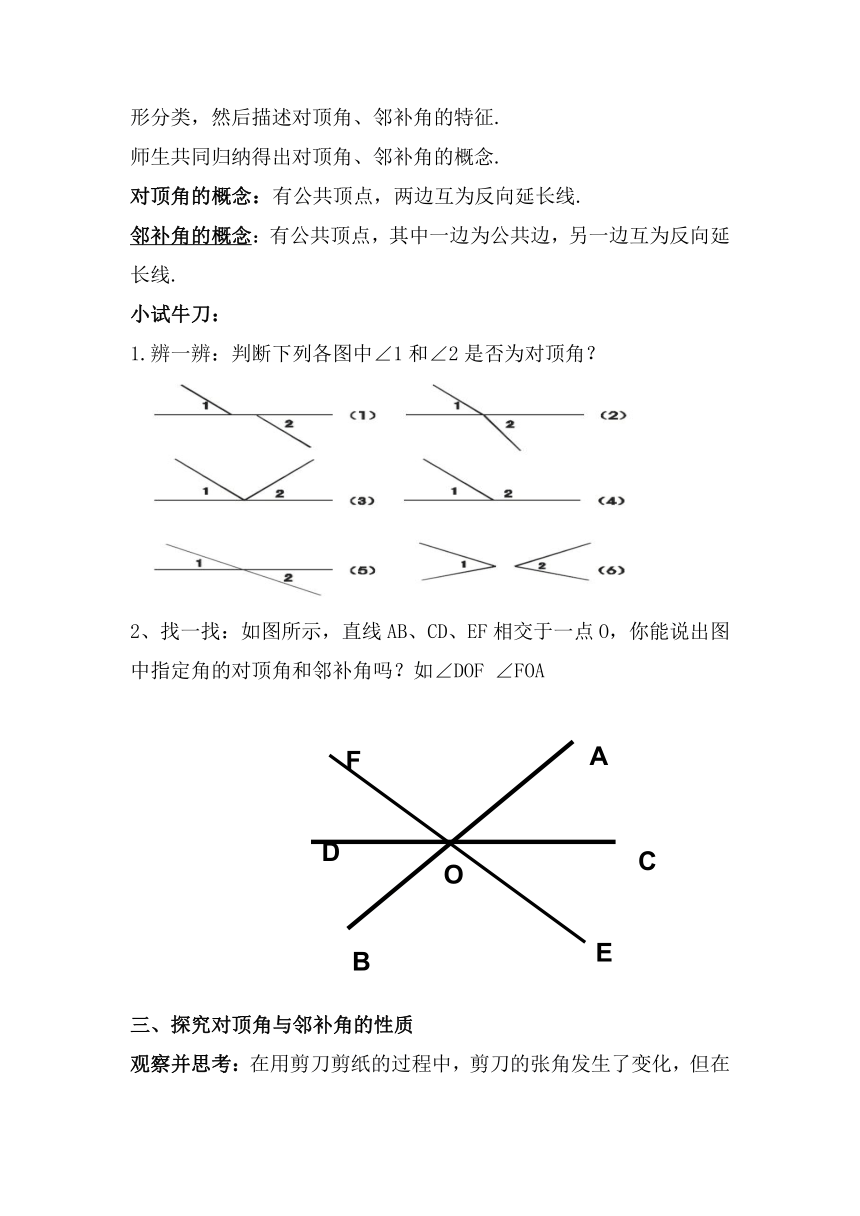
1.辨一辨:判断下列各图中∠1和∠2是否为对顶角?
2、找一找:如图所示,直线AB、CD、EF相交于一点O,你能说出图中指定角的对顶角和邻补角吗?如∠DOF ∠FOA
三、探究对顶角与邻补角的性质
观察并思考:在用剪刀剪纸的过程中,剪刀的张角发生了变化,但在这一过程中有没有不变的数量关系呢?大家先猜想一下对顶角∠1与∠3,∠2与∠4的关系,再用量角器测量一下不同情况下∠1与∠3,∠2与∠4的度数,来验证你的猜想。
教师提出问题作为学生的任务, 让学生去合作讨论完成.
这一过程的重点是对顶角的性质的得出,教师应关注学生能否得出准确的结论,同时对对顶角相等这一结论的得出,师生共同完成用规范的语言给出推理过程.
收获新知:
直线AB、CD相交于点O, ∠1与∠3、∠2与∠4互为对顶角,有∠2=∠4.你能说出其中的道理吗?
同理可得:∠1=∠3
对顶角的性质:对顶角相等.
四、应用新知:
1、如图,直线a、b相交,∠1=50°,求 ∠2=
∠3= 、∠ 4= .
2、如图,直线AB、CD相交于O,∠AOC=80°,若OE为∠BOD的角平分线;求∠1=
变式:若∠AOD=100°,求∠1=( ).
3、(回归生活)、图中是对顶角量角器,你能说出用它测量角的原理吗?
课堂小结
通过本节课的学习,谈谈你对对顶角、邻补角的认识.
让学生多说,培养学生的梳理、说理能力.
布置作业
必做:习题10.1第1、2题.
选做:要测量两堵墙所成的∠AOB的度数,但人不能进入围墙,如何测量?
A
B
C
D
E
F
O
A
C
B
D
E
1
2
)
)
O
教学目标:
在具体生活情境中感受两条直线相交的情形,进一步体会对顶角、邻补角等概念的形成过程.
准确理解对顶角、邻补角的概念,并能在具体图形中熟练辨认对顶角、邻补角.
3、理解对顶角、邻补角的数量关系,并能进行相关简单计算.
教学重难点:
重点: 对顶角、邻补角的概念,对顶角的性质.
难点:对顶角性质的理解与应用.
教学过程:
一.创设情境 导入新课
1、课件展示剪刀图片,让学生观察、感受剪刀中的相交线,从而引出课题,并介绍相交线及相关的概念.
2、结合你的生活,你能在身边再找出一些相交线的实例吗
让学生进一步在具体生活情景中感受两条直线相交的情形.
二、探究对顶角、邻补角的概念
思考:两条直线相交,形成的小于平角的角有几个?将这些角两两配对组合,共能组成几对角?根据这种位置关系将它们分类,能分几类?
学生分组讨论在具体图形中得出的两条相交线构成的四个角,根据图形分类,然后描述对顶角、邻补角的特征.
师生共同归纳得出对顶角、邻补角的概念.
对顶角的概念:有公共顶点,两边互为反向延长线.
邻补角的概念:有公共顶点,其中一边为公共边,另一边互为反向延长线.
小试牛刀:
1.辨一辨:判断下列各图中∠1和∠2是否为对顶角?
2、找一找:如图所示,直线AB、CD、EF相交于一点O,你能说出图中指定角的对顶角和邻补角吗?如∠DOF ∠FOA
三、探究对顶角与邻补角的性质
观察并思考:在用剪刀剪纸的过程中,剪刀的张角发生了变化,但在这一过程中有没有不变的数量关系呢?大家先猜想一下对顶角∠1与∠3,∠2与∠4的关系,再用量角器测量一下不同情况下∠1与∠3,∠2与∠4的度数,来验证你的猜想。
教师提出问题作为学生的任务, 让学生去合作讨论完成.
这一过程的重点是对顶角的性质的得出,教师应关注学生能否得出准确的结论,同时对对顶角相等这一结论的得出,师生共同完成用规范的语言给出推理过程.
收获新知:
直线AB、CD相交于点O, ∠1与∠3、∠2与∠4互为对顶角,有∠2=∠4.你能说出其中的道理吗?
同理可得:∠1=∠3
对顶角的性质:对顶角相等.
四、应用新知:
1、如图,直线a、b相交,∠1=50°,求 ∠2=
∠3= 、∠ 4= .
2、如图,直线AB、CD相交于O,∠AOC=80°,若OE为∠BOD的角平分线;求∠1=
变式:若∠AOD=100°,求∠1=( ).
3、(回归生活)、图中是对顶角量角器,你能说出用它测量角的原理吗?
课堂小结
通过本节课的学习,谈谈你对对顶角、邻补角的认识.
让学生多说,培养学生的梳理、说理能力.
布置作业
必做:习题10.1第1、2题.
选做:要测量两堵墙所成的∠AOB的度数,但人不能进入围墙,如何测量?
A
B
C
D
E
F
O
A
C
B
D
E
1
2
)
)
O
