2024-2025学年山东省淄博市桓台二中高一(下)月考数学试卷(6月份)(含答案)
文档属性
| 名称 | 2024-2025学年山东省淄博市桓台二中高一(下)月考数学试卷(6月份)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 194.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 21:10:36 | ||
图片预览




文档简介
2024-2025学年山东省淄博市桓台二中高一(下)月考数学试卷(6月份)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知i是虚数单位,则的虚部为( )
A. 1 B. i C. D.
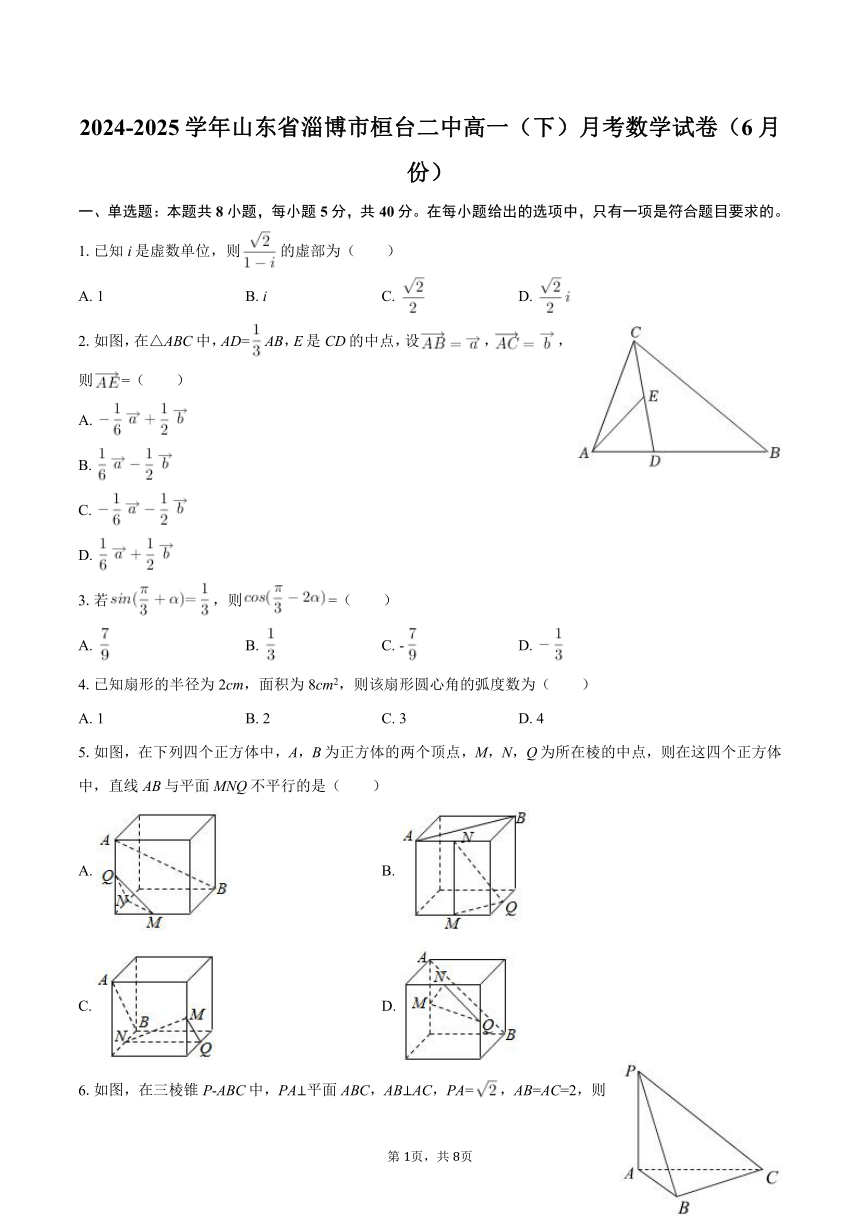
2.如图,在△ABC中,AD=AB,E是CD的中点,设,,则=( )
A.
B.
C.
D.
3.若,则=( )
A. B. C. - D.
4.已知扇形的半径为2cm,面积为8cm2,则该扇形圆心角的弧度数为( )
A. 1 B. 2 C. 3 D. 4
5.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )
A. B.
C. D.
6.如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=,AB=AC=2,则点A到平面PBC的距离为( )
A. 1
B.
C.
D.
7.已知平面向量,满足 (2-)=5,且||=2,||=3,则向量与的夹角的余弦值为( )
A. 1 B. -1 C. D. -
8.宋代是中国瓷器的黄金时代,涌现出了五大名窑:汝窑、官窑、哥窑、钧窑、定窑.其中汝窑被认为是五大名窑之首.如图1,这是汝窑双耳罐,该汝窑双耳罐可近似看成由两个圆台拼接而成,其直观图如图2所示.已知该汝窑双耳罐下底面圆的直径是12厘米,中间圆的直径是20厘米,上底面圆的直径是8厘米,高是14厘米,且上、下两圆台的高之比是3:4,则该汝窑双耳罐的体积是( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得2分,有选错的得0分。
9.已知m、n是两条不同的直线,α、β是两个不重合的平面,给定下列四个命题,其中是真命题的是( )
A. 若m⊥n,n α,则m⊥α B. 若m⊥α,n α,则m⊥n
C. 若m⊥α,n⊥α,则m∥n D. 若m α,n β,α∥β,则m∥n
10.已知向量=(-1,1),=(-2,3),=(m,n-1),则( )
A. |-|=
B. 当(+)⊥时,4n-3m=4
C. 当∥时,m-n=1
D. 在上的投影向量的坐标为
11.已知正方体ABCD-A1B1C1D1的棱长为1,E是DD1的中点,则下列选项中正确的是( )
A. AC⊥B1E B. B1C∥平面A1BD
C. 三棱锥C1-B1CE的体积为 D. 异面直线B1C与BD所成的角为45°
三、填空题:本题共3小题,每小题5分,共15分。
12.边长为2的菱形ABCD中,∠BAD=60°,E、F分别为BC、CD的中点,则= ______.
13.在△ABC中,内角A,B,C的对边分别为a,b,c,若a=3,b=3,c=4,则= ______.
14.如图,点M是正方体ABCD-A1B1C1D1的棱CD的中点,则异面直线AM与BC1所成角的余弦值是______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
已知△ABC的内角A,B,C所对的边分别为a,b,c,且acosC+ccosA=2bcosA.
(1)求角A;
(2)若,b=2,求边c及△ABC的面积;
(3)在(2)的条件下,求sin(2B-A)的值.
16.(本小题15分)
已知函数.
(1)求的值及f(x)的对称轴;
(2)求f(x)在上的值域;
(3)将f(x)的图象向左平移个单位得到函数g(x)的图象,求g(x)的单调递增区间.
17.(本小题15分)
如图,已知四棱锥S-ABCD中,底面ABCD是平行四边形,E为侧棱SC的中点.
(1)求证:SA∥平面EDB;
(2)若F为侧棱AB的中点,求证:EF∥平面SAD;
(3)设平面SAB∩平面SCD=l,求证:AB∥l.
18.(本小题17分)
已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,CD=2AB=2AD=2,侧面PAD是正三角形且垂直于面ABCD,E是PC中点.
(1)求证:BE∥面PAD;
(2)求证:BE⊥平面PCD;
(3)求BD与平面PDC所成角的正弦值.
19.(本小题17分)
如图,在四棱锥P-ABCD中,底面ABCD为矩形,且AB=3,AD=2,侧面PAD是等腰三角形,且PA=PD=,侧面PAD⊥底面ABCD.(Ⅰ)求证:AP⊥平面PCD;
(Ⅱ)求侧面PBC与底面ABCD所成二面角的正弦值.
1.【答案】C
2.【答案】D
3.【答案】C
4.【答案】D
5.【答案】A
6.【答案】A
7.【答案】C
8.【答案】D
9.【答案】BC
10.【答案】ABD
11.【答案】AB
12.【答案】
13.【答案】1
14.【答案】
15.【答案】解:(1)因为acosC+ccosA=2bcosA,
由正弦定理可得sinAcosC+sinCcosA=2sinBcosA,
即sin(A+C)=2sinBcosA,
即sinB=2sinBcosA,
又B∈(0,π),
所以sinB>0,
则,
又A∈(0,π),
所以.
(2)由余弦定理得,
整理得c2-2c-3=0,
解得c=3或c=-1(舍去),
所以△ABC的面积.
(3)由正弦定理得,
即,
解得,
因为c>a>b,
故∠B为锐角,故,
所以,
,
所以sin(2B-A)=sin2BcosA-cos2BsinA
=.
16.【答案】,对称轴方程为;
;
.
17.【答案】证明:(1)设AC∩BD=O,连接AC,OE,因为ABCD是平行四边形,故AO=OC,
又E为侧棱SC的中点,故SA∥EO
又SA 平面EDB,EO 平面EDB,
故SA∥平面EDB;
(2)若F为AB的中点,DO=BO,则AD∥FO,
又FO 平面SAD,AD 平面SAD,故FO∥平面SAD.
又SA∥EO,EO 平面SAD,SA 平面SAD,
故EO∥平面SAD.
又EO∩FO=O,EO,FO 平面EOF,
故平面EOF∥平面SAD,
又EF 平面EOF,
故EF∥平面SAD;
(3)因为AB∥CD,AB 平面SCD,CD 平面SCD,故AB∥平面SCD.
又平面SAB∩平面SCD=l,AB 平面SAB,
故AB∥l.
18.【答案】证明:取PD的中点F,连接AF、EF,
因为E是PC中点,所以EF∥CD,,
因为AB∥CD,CD=2AB,所以EF∥AB,EF=AB,
所以四边形ABEF是平行四边形,所以BE∥AF,
又因为BE 平面PAD,AF 平面PAD,
所以BE∥平面PAD;
证明:因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,CD⊥AD,
所以CD⊥平面PAD,
因为AF 平面PAD,所以CD⊥AF,
因为等边三角形PAD,F为PD的中点,所以AF⊥PD,
又因为CD∩PD=D,CD、PD 平面PCD,所以AF⊥平面PCD,
因为AF∥BE,所以BE⊥平面PCD;
.
19.【答案】(Ⅰ)证明:在△APD中,AD=2,,
∴AD2=AP2+DP2,∴AP⊥DP,
又∵侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,
AD⊥CD,CD 平面ABCD,∴CD⊥平面APD,∴CD⊥AP,
∵CD∩DP=D,∴AP⊥平面PCD;
(Ⅱ)解:取AD的中点为M,连接PM,∵PA=PD,所以PM⊥AD,
又∵侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,
∴PM⊥平面ABCD,过点M作MG⊥BC,垂足为G,连接PG,
∴BC⊥平面PMG,∴∠PGM为侧面PBC与底面ABCD所成二面角的平面角,
在直角△PMG中,AD=1,MG=3,∴,
∴,
即侧面PBC与底面ABCD所成二面角的正弦值为.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知i是虚数单位,则的虚部为( )
A. 1 B. i C. D.
2.如图,在△ABC中,AD=AB,E是CD的中点,设,,则=( )
A.
B.
C.
D.
3.若,则=( )
A. B. C. - D.
4.已知扇形的半径为2cm,面积为8cm2,则该扇形圆心角的弧度数为( )
A. 1 B. 2 C. 3 D. 4
5.如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( )
A. B.
C. D.
6.如图,在三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,PA=,AB=AC=2,则点A到平面PBC的距离为( )
A. 1
B.
C.
D.
7.已知平面向量,满足 (2-)=5,且||=2,||=3,则向量与的夹角的余弦值为( )
A. 1 B. -1 C. D. -
8.宋代是中国瓷器的黄金时代,涌现出了五大名窑:汝窑、官窑、哥窑、钧窑、定窑.其中汝窑被认为是五大名窑之首.如图1,这是汝窑双耳罐,该汝窑双耳罐可近似看成由两个圆台拼接而成,其直观图如图2所示.已知该汝窑双耳罐下底面圆的直径是12厘米,中间圆的直径是20厘米,上底面圆的直径是8厘米,高是14厘米,且上、下两圆台的高之比是3:4,则该汝窑双耳罐的体积是( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。全部选对的得6分,部分选对的得2分,有选错的得0分。
9.已知m、n是两条不同的直线,α、β是两个不重合的平面,给定下列四个命题,其中是真命题的是( )
A. 若m⊥n,n α,则m⊥α B. 若m⊥α,n α,则m⊥n
C. 若m⊥α,n⊥α,则m∥n D. 若m α,n β,α∥β,则m∥n
10.已知向量=(-1,1),=(-2,3),=(m,n-1),则( )
A. |-|=
B. 当(+)⊥时,4n-3m=4
C. 当∥时,m-n=1
D. 在上的投影向量的坐标为
11.已知正方体ABCD-A1B1C1D1的棱长为1,E是DD1的中点,则下列选项中正确的是( )
A. AC⊥B1E B. B1C∥平面A1BD
C. 三棱锥C1-B1CE的体积为 D. 异面直线B1C与BD所成的角为45°
三、填空题:本题共3小题,每小题5分,共15分。
12.边长为2的菱形ABCD中,∠BAD=60°,E、F分别为BC、CD的中点,则= ______.
13.在△ABC中,内角A,B,C的对边分别为a,b,c,若a=3,b=3,c=4,则= ______.
14.如图,点M是正方体ABCD-A1B1C1D1的棱CD的中点,则异面直线AM与BC1所成角的余弦值是______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题13分)
已知△ABC的内角A,B,C所对的边分别为a,b,c,且acosC+ccosA=2bcosA.
(1)求角A;
(2)若,b=2,求边c及△ABC的面积;
(3)在(2)的条件下,求sin(2B-A)的值.
16.(本小题15分)
已知函数.
(1)求的值及f(x)的对称轴;
(2)求f(x)在上的值域;
(3)将f(x)的图象向左平移个单位得到函数g(x)的图象,求g(x)的单调递增区间.
17.(本小题15分)
如图,已知四棱锥S-ABCD中,底面ABCD是平行四边形,E为侧棱SC的中点.
(1)求证:SA∥平面EDB;
(2)若F为侧棱AB的中点,求证:EF∥平面SAD;
(3)设平面SAB∩平面SCD=l,求证:AB∥l.
18.(本小题17分)
已知四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,CD=2AB=2AD=2,侧面PAD是正三角形且垂直于面ABCD,E是PC中点.
(1)求证:BE∥面PAD;
(2)求证:BE⊥平面PCD;
(3)求BD与平面PDC所成角的正弦值.
19.(本小题17分)
如图,在四棱锥P-ABCD中,底面ABCD为矩形,且AB=3,AD=2,侧面PAD是等腰三角形,且PA=PD=,侧面PAD⊥底面ABCD.(Ⅰ)求证:AP⊥平面PCD;
(Ⅱ)求侧面PBC与底面ABCD所成二面角的正弦值.
1.【答案】C
2.【答案】D
3.【答案】C
4.【答案】D
5.【答案】A
6.【答案】A
7.【答案】C
8.【答案】D
9.【答案】BC
10.【答案】ABD
11.【答案】AB
12.【答案】
13.【答案】1
14.【答案】
15.【答案】解:(1)因为acosC+ccosA=2bcosA,
由正弦定理可得sinAcosC+sinCcosA=2sinBcosA,
即sin(A+C)=2sinBcosA,
即sinB=2sinBcosA,
又B∈(0,π),
所以sinB>0,
则,
又A∈(0,π),
所以.
(2)由余弦定理得,
整理得c2-2c-3=0,
解得c=3或c=-1(舍去),
所以△ABC的面积.
(3)由正弦定理得,
即,
解得,
因为c>a>b,
故∠B为锐角,故,
所以,
,
所以sin(2B-A)=sin2BcosA-cos2BsinA
=.
16.【答案】,对称轴方程为;
;
.
17.【答案】证明:(1)设AC∩BD=O,连接AC,OE,因为ABCD是平行四边形,故AO=OC,
又E为侧棱SC的中点,故SA∥EO
又SA 平面EDB,EO 平面EDB,
故SA∥平面EDB;
(2)若F为AB的中点,DO=BO,则AD∥FO,
又FO 平面SAD,AD 平面SAD,故FO∥平面SAD.
又SA∥EO,EO 平面SAD,SA 平面SAD,
故EO∥平面SAD.
又EO∩FO=O,EO,FO 平面EOF,
故平面EOF∥平面SAD,
又EF 平面EOF,
故EF∥平面SAD;
(3)因为AB∥CD,AB 平面SCD,CD 平面SCD,故AB∥平面SCD.
又平面SAB∩平面SCD=l,AB 平面SAB,
故AB∥l.
18.【答案】证明:取PD的中点F,连接AF、EF,
因为E是PC中点,所以EF∥CD,,
因为AB∥CD,CD=2AB,所以EF∥AB,EF=AB,
所以四边形ABEF是平行四边形,所以BE∥AF,
又因为BE 平面PAD,AF 平面PAD,
所以BE∥平面PAD;
证明:因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,CD⊥AD,
所以CD⊥平面PAD,
因为AF 平面PAD,所以CD⊥AF,
因为等边三角形PAD,F为PD的中点,所以AF⊥PD,
又因为CD∩PD=D,CD、PD 平面PCD,所以AF⊥平面PCD,
因为AF∥BE,所以BE⊥平面PCD;
.
19.【答案】(Ⅰ)证明:在△APD中,AD=2,,
∴AD2=AP2+DP2,∴AP⊥DP,
又∵侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,
AD⊥CD,CD 平面ABCD,∴CD⊥平面APD,∴CD⊥AP,
∵CD∩DP=D,∴AP⊥平面PCD;
(Ⅱ)解:取AD的中点为M,连接PM,∵PA=PD,所以PM⊥AD,
又∵侧面PAD⊥底面ABCD,侧面PAD∩底面ABCD=AD,
∴PM⊥平面ABCD,过点M作MG⊥BC,垂足为G,连接PG,
∴BC⊥平面PMG,∴∠PGM为侧面PBC与底面ABCD所成二面角的平面角,
在直角△PMG中,AD=1,MG=3,∴,
∴,
即侧面PBC与底面ABCD所成二面角的正弦值为.
第1页,共1页
同课章节目录
