江苏省无锡市新吴实验中学2024-2025学年八年级下学期3月月考数学试卷(含部分答案)
文档属性
| 名称 | 江苏省无锡市新吴实验中学2024-2025学年八年级下学期3月月考数学试卷(含部分答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 124.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 16:49:30 | ||
图片预览


文档简介
2024-2025学年江苏省无锡市新吴实验中学八年级(下)月考数学试卷(3月份)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列新能源汽车车标中,既是轴对称图形也是中心对称图形的是( )
A. B. C. D.
2.今年我市有4万名学生参加中考,为了了解这些考生的数学成绩,从中抽取2000名考生的数学成绩进行统计分析.在这个问题中,下列说法正确的是( )
A. 这4万名考生的全体是总体 B. 每个考生是个体
C. 2000名考生是总体的一个样本 D. 样本容量是2000
3.下列计算正确的是( )
A. B. C. D.
4.下列各式:,2πr,,中,是分式的共有( )
A. 1个 B. 2个 C. 3个 D. 4个
5.菱形具有而矩形不一定具有的性质是( )
A. 对角线互相平分 B. 对角线相等 C. 邻边互相垂直 D. 对角线互相垂直
6.下列各式从左到右的变形中,正确的是( )
A. B. C. D.
7.如图,在矩形ABCD中,对角线AC,BD交于点E,DF⊥AC于F点,若∠ADF=2∠FDC,则下列结论不正确的是( )
A. BE=DF B. BC=2DF C. AE=2EF D. AB=2CF
8.如图,有一个平行四边形ABCD和一个正方形CEFG,其中点E在边AD上,若∠ECD=49°,∠AEF=34°,则∠B=( )
A. 55°
B. 65°
C. 75°
D. 60°
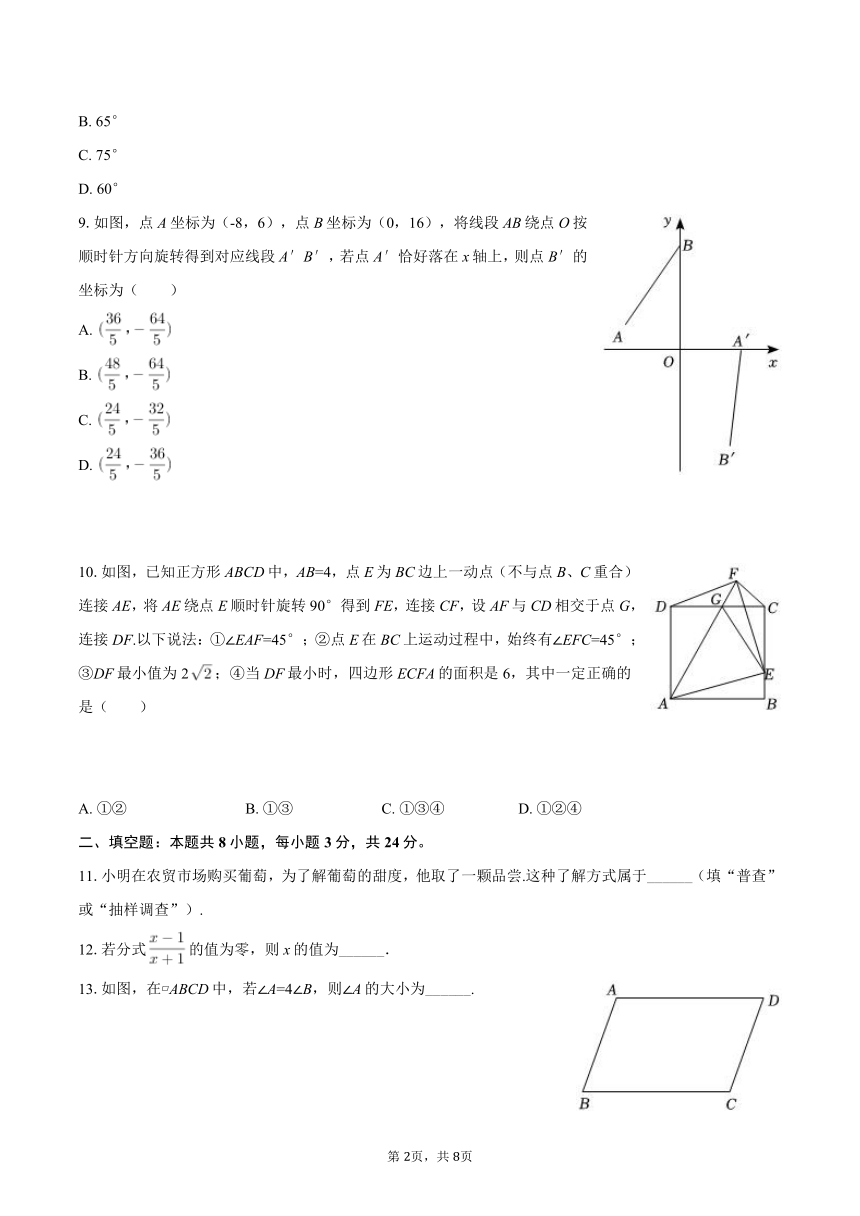
9.如图,点A坐标为(-8,6),点B坐标为(0,16),将线段AB绕点O按顺时针方向旋转得到对应线段A′B′,若点A′恰好落在x轴上,则点B′的坐标为( )
A.
B.
C.
D.
10.如图,已知正方形ABCD中,AB=4,点E为BC边上一动点(不与点B、C重合),连接AE,将AE绕点E顺时针旋转90°得到FE,连接CF,设AF与CD相交于点G,连接DF.以下说法:①∠EAF=45°;②点E在BC上运动过程中,始终有∠EFC=45°;③DF最小值为2;④当DF最小时,四边形ECFA的面积是6,其中一定正确的是( )
A. ①② B. ①③ C. ①③④ D. ①②④
二、填空题:本题共8小题,每小题3分,共24分。
11.小明在农贸市场购买葡萄,为了解葡萄的甜度,他取了一颗品尝.这种了解方式属于______(填“普查”或“抽样调查”).
12.若分式的值为零,则x的值为______.
13.如图,在 ABCD中,若∠A=4∠B,则∠A的大小为______.
14.二次根式有意义,那么x的取值范围是______.
15.如图,每个小正方形的边长为1,在△ABC中,点D,E分别为AB,AC的中点,则线段DE的长为______.
16.如图,矩形ABCD中,AB=6,AD=8,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值是______.
17.如图,已知菱形ABCD中,,点E为CD中点,连接BE,点P为线段BE上动点,连接PD、PA,若∠APD=60°,则PE=______.
18.如图,在△ABC中,∠ACB=90°,AB=6,BC=4.将△ABC绕点A旋转得△AB'C',连接B'C,B'B,则△B'CB面积的最大值为______.
三、解答题:本题共7小题,共56分。解答应写出文字说明,证明过程或演算步骤。
19.(本小题8分)
(1)(-)-2+-(-4)0
(2)(-1)2-(3+)(3-)
20.(本小题8分)
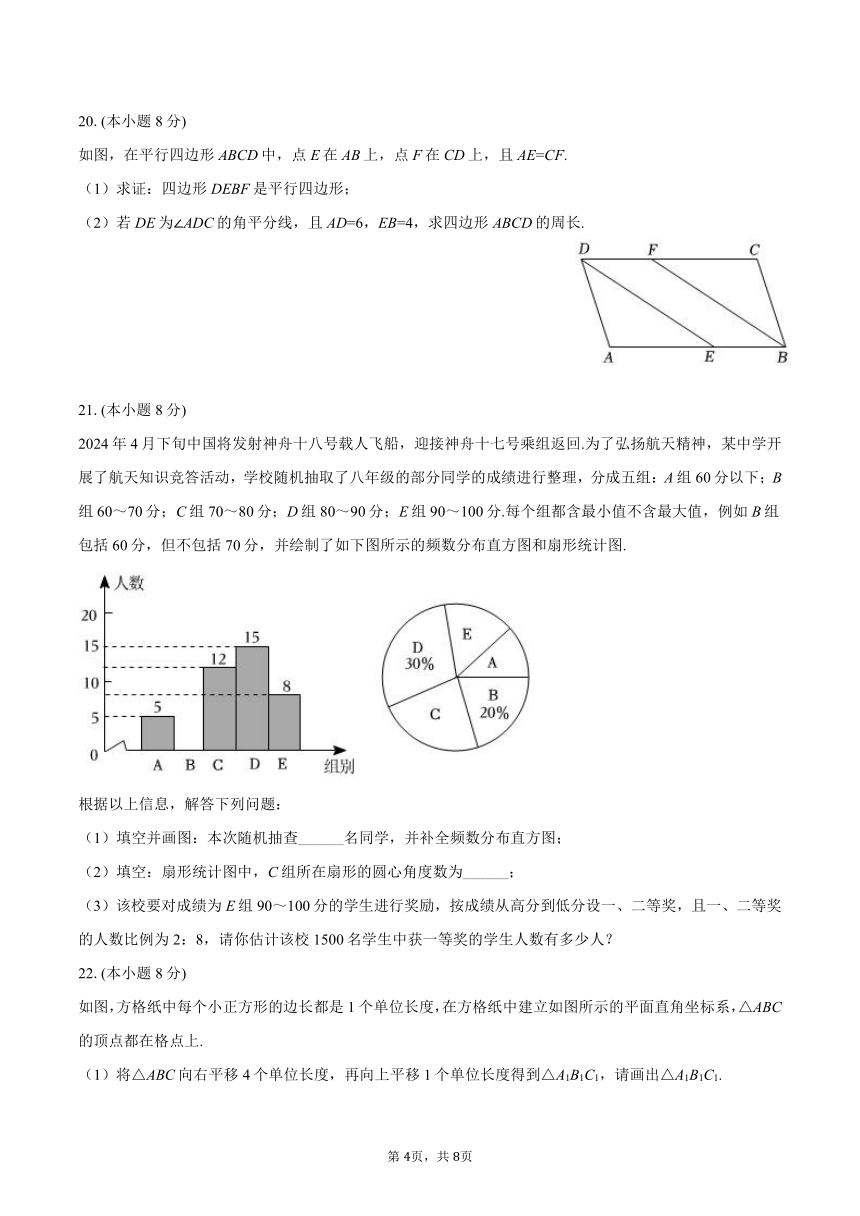
如图,在平行四边形ABCD中,点E在AB上,点F在CD上,且AE=CF.
(1)求证:四边形DEBF是平行四边形;
(2)若DE为∠ADC的角平分线,且AD=6,EB=4,求四边形ABCD的周长.
21.(本小题8分)
2024年4月下旬中国将发射神舟十八号载人飞船,迎接神舟十七号乘组返回.为了弘扬航天精神,某中学开展了航天知识竞答活动,学校随机抽取了八年级的部分同学的成绩进行整理,分成五组:A组60分以下;B组60~70分;C组70~80分;D组80~90分;E组90~100分.每个组都含最小值不含最大值,例如B组包括60分,但不包括70分,并绘制了如下图所示的频数分布直方图和扇形统计图.
根据以上信息,解答下列问题:
(1)填空并画图:本次随机抽查______名同学,并补全频数分布直方图;
(2)填空:扇形统计图中,C组所在扇形的圆心角度数为______;
(3)该校要对成绩为E组90~100分的学生进行奖励,按成绩从高分到低分设一、二等奖,且一、二等奖的人数比例为2:8,请你估计该校1500名学生中获一等奖的学生人数有多少人?
22.(本小题8分)
如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上.
(1)将△ABC向右平移4个单位长度,再向上平移1个单位长度得到△A1B1C1,请画出△A1B1C1.
(2)画出△ABC关于点O的中心对称图形△A2B2C2;
(3)若将△A1B1C1绕某一点旋转可得到△A2B2C2,则旋转中心的坐标为______.
23.(本小题8分)
如图,已知△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹).
(1)作菱形AMNP,使点M,N、P在边AB、BC、CA上;
(2)若∠C=90°,∠A=60°,AC=3时,则菱形AMNP的面积为______.
24.(本小题8分)
阅读材料:
像,…
两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.
例如,、与,2+3与等都是互为有理化因式,在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
根据以上阅读材料回答下列问题:
(1)计算:=______;(n≥1)=______;
(2)计算:.
25.(本小题8分)
如图,在平面直角坐标系中,点A(4,0),B(6,3),C(0,3).
(1)若动点P从原点O出发,以每秒2个单位长度沿着x轴正方向运动,动点Q从点B出发,以每秒1个单位长度向点C运动,当点Q到达点C处时,两点都停止运动.设运动时间为t(秒).若以A、B、P、Q四个点为顶点的四边形是平行四边形,求此时t的值;
(2)点M在x轴上,平面内是否存在点N,当以A、C、M、N为顶点的四边形是菱形时,则所有满足条件的点N的坐标为______.
1.【答案】D
2.【答案】D
3.【答案】C
4.【答案】B
5.【答案】D
6.【答案】A
7.【答案】A
8.【答案】C
9.【答案】B
10.【答案】B
11.【答案】抽样调查
12.【答案】1
13.【答案】144°
14.【答案】x>-5
15.【答案】
16.【答案】4.8
17.【答案】1
18.【答案】12
19.【答案】解:(1)原式=4+3-1
=3+3;
(2)原式=6-2+1-(9-5)
=3-2.
20.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE=CF,
∴AB-AE=CD-CF,
∴BE=DF,
∴四边形DEBF是平行四边形;
(2)解:∵AB∥CD,
∴∠EDC=∠AED,
∵DE为∠ADC的平分线,
∴∠ADE=∠EDC,
∴∠ADE=∠AED,
∴AE=AD=6,
∴AB=AE+EB=6+4=10,
∴四边形ABCD的周长为2(AB+AD)=2×(10+6)=32.
21.【答案】50;补全频数分布直方图见解答.
86.4°.
约有48 人.
22.【答案】见解答.
见解答.
(2,).
23.【答案】见解析; 2.
24.【答案】;-;
44.
25.【答案】t=或4时,以A,B,P,Q为顶点的四边形为平行四边形.
(-5,3),(5,3),(0,-3).
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列新能源汽车车标中,既是轴对称图形也是中心对称图形的是( )
A. B. C. D.
2.今年我市有4万名学生参加中考,为了了解这些考生的数学成绩,从中抽取2000名考生的数学成绩进行统计分析.在这个问题中,下列说法正确的是( )
A. 这4万名考生的全体是总体 B. 每个考生是个体
C. 2000名考生是总体的一个样本 D. 样本容量是2000
3.下列计算正确的是( )
A. B. C. D.
4.下列各式:,2πr,,中,是分式的共有( )
A. 1个 B. 2个 C. 3个 D. 4个
5.菱形具有而矩形不一定具有的性质是( )
A. 对角线互相平分 B. 对角线相等 C. 邻边互相垂直 D. 对角线互相垂直
6.下列各式从左到右的变形中,正确的是( )
A. B. C. D.
7.如图,在矩形ABCD中,对角线AC,BD交于点E,DF⊥AC于F点,若∠ADF=2∠FDC,则下列结论不正确的是( )
A. BE=DF B. BC=2DF C. AE=2EF D. AB=2CF
8.如图,有一个平行四边形ABCD和一个正方形CEFG,其中点E在边AD上,若∠ECD=49°,∠AEF=34°,则∠B=( )
A. 55°
B. 65°
C. 75°
D. 60°
9.如图,点A坐标为(-8,6),点B坐标为(0,16),将线段AB绕点O按顺时针方向旋转得到对应线段A′B′,若点A′恰好落在x轴上,则点B′的坐标为( )
A.
B.
C.
D.
10.如图,已知正方形ABCD中,AB=4,点E为BC边上一动点(不与点B、C重合),连接AE,将AE绕点E顺时针旋转90°得到FE,连接CF,设AF与CD相交于点G,连接DF.以下说法:①∠EAF=45°;②点E在BC上运动过程中,始终有∠EFC=45°;③DF最小值为2;④当DF最小时,四边形ECFA的面积是6,其中一定正确的是( )
A. ①② B. ①③ C. ①③④ D. ①②④
二、填空题:本题共8小题,每小题3分,共24分。
11.小明在农贸市场购买葡萄,为了解葡萄的甜度,他取了一颗品尝.这种了解方式属于______(填“普查”或“抽样调查”).
12.若分式的值为零,则x的值为______.
13.如图,在 ABCD中,若∠A=4∠B,则∠A的大小为______.
14.二次根式有意义,那么x的取值范围是______.
15.如图,每个小正方形的边长为1,在△ABC中,点D,E分别为AB,AC的中点,则线段DE的长为______.
16.如图,矩形ABCD中,AB=6,AD=8,对角线AC、BD相交于点O,点P是线段AD上任意一点,且PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值是______.
17.如图,已知菱形ABCD中,,点E为CD中点,连接BE,点P为线段BE上动点,连接PD、PA,若∠APD=60°,则PE=______.
18.如图,在△ABC中,∠ACB=90°,AB=6,BC=4.将△ABC绕点A旋转得△AB'C',连接B'C,B'B,则△B'CB面积的最大值为______.
三、解答题:本题共7小题,共56分。解答应写出文字说明,证明过程或演算步骤。
19.(本小题8分)
(1)(-)-2+-(-4)0
(2)(-1)2-(3+)(3-)
20.(本小题8分)
如图,在平行四边形ABCD中,点E在AB上,点F在CD上,且AE=CF.
(1)求证:四边形DEBF是平行四边形;
(2)若DE为∠ADC的角平分线,且AD=6,EB=4,求四边形ABCD的周长.
21.(本小题8分)
2024年4月下旬中国将发射神舟十八号载人飞船,迎接神舟十七号乘组返回.为了弘扬航天精神,某中学开展了航天知识竞答活动,学校随机抽取了八年级的部分同学的成绩进行整理,分成五组:A组60分以下;B组60~70分;C组70~80分;D组80~90分;E组90~100分.每个组都含最小值不含最大值,例如B组包括60分,但不包括70分,并绘制了如下图所示的频数分布直方图和扇形统计图.
根据以上信息,解答下列问题:
(1)填空并画图:本次随机抽查______名同学,并补全频数分布直方图;
(2)填空:扇形统计图中,C组所在扇形的圆心角度数为______;
(3)该校要对成绩为E组90~100分的学生进行奖励,按成绩从高分到低分设一、二等奖,且一、二等奖的人数比例为2:8,请你估计该校1500名学生中获一等奖的学生人数有多少人?
22.(本小题8分)
如图,方格纸中每个小正方形的边长都是1个单位长度,在方格纸中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上.
(1)将△ABC向右平移4个单位长度,再向上平移1个单位长度得到△A1B1C1,请画出△A1B1C1.
(2)画出△ABC关于点O的中心对称图形△A2B2C2;
(3)若将△A1B1C1绕某一点旋转可得到△A2B2C2,则旋转中心的坐标为______.
23.(本小题8分)
如图,已知△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹).
(1)作菱形AMNP,使点M,N、P在边AB、BC、CA上;
(2)若∠C=90°,∠A=60°,AC=3时,则菱形AMNP的面积为______.
24.(本小题8分)
阅读材料:
像,…
两个含有二次根式的代数式相乘,积不含有二次根式,我们称这两个代数式互为有理化因式.
例如,、与,2+3与等都是互为有理化因式,在进行二次根式计算时,利用有理化因式,可以化去分母中的根号.
根据以上阅读材料回答下列问题:
(1)计算:=______;(n≥1)=______;
(2)计算:.
25.(本小题8分)
如图,在平面直角坐标系中,点A(4,0),B(6,3),C(0,3).
(1)若动点P从原点O出发,以每秒2个单位长度沿着x轴正方向运动,动点Q从点B出发,以每秒1个单位长度向点C运动,当点Q到达点C处时,两点都停止运动.设运动时间为t(秒).若以A、B、P、Q四个点为顶点的四边形是平行四边形,求此时t的值;
(2)点M在x轴上,平面内是否存在点N,当以A、C、M、N为顶点的四边形是菱形时,则所有满足条件的点N的坐标为______.
1.【答案】D
2.【答案】D
3.【答案】C
4.【答案】B
5.【答案】D
6.【答案】A
7.【答案】A
8.【答案】C
9.【答案】B
10.【答案】B
11.【答案】抽样调查
12.【答案】1
13.【答案】144°
14.【答案】x>-5
15.【答案】
16.【答案】4.8
17.【答案】1
18.【答案】12
19.【答案】解:(1)原式=4+3-1
=3+3;
(2)原式=6-2+1-(9-5)
=3-2.
20.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AE=CF,
∴AB-AE=CD-CF,
∴BE=DF,
∴四边形DEBF是平行四边形;
(2)解:∵AB∥CD,
∴∠EDC=∠AED,
∵DE为∠ADC的平分线,
∴∠ADE=∠EDC,
∴∠ADE=∠AED,
∴AE=AD=6,
∴AB=AE+EB=6+4=10,
∴四边形ABCD的周长为2(AB+AD)=2×(10+6)=32.
21.【答案】50;补全频数分布直方图见解答.
86.4°.
约有48 人.
22.【答案】见解答.
见解答.
(2,).
23.【答案】见解析; 2.
24.【答案】;-;
44.
25.【答案】t=或4时,以A,B,P,Q为顶点的四边形为平行四边形.
(-5,3),(5,3),(0,-3).
第1页,共1页
同课章节目录
