期末专题训练(五) 一次函数 同步练(含答案)2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 期末专题训练(五) 一次函数 同步练(含答案)2025-2026学年数学苏科版(2024)八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 122.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 00:00:00 | ||
图片预览

文档简介
期末专题训练(五) 一 次 函 数
考点一 变量与函数
1 (2024南通崇川月考)下列曲线中,不能表示y是x的函数的是( )
A B C D
2 (2024江西)将常温中的温度计插入一杯60 ℃的热水(恒温)中,温度计的读数y(单位:℃)与时间x(单位:min)的关系用图象可近似表示为( )
A B D C
考点二 正比例函数与一次函数的图象与性质
3 (2025苏州模拟)若点(3,-4)在正比例函数y=kx(k≠0)的图象上,则k的值为( )
A. -12 B. 12 C. - D. -
4 (2024扬州邗江期末)对于一次函数y=-2x-3,下列说法中不正确的是( )
A. 图象不经过第一象限
B. 图象与y轴的交点坐标为(0,-3)
C. 若点(-1,y1),(4,y2)在一次函数y=-2x-3的图象上,则y1<y2
D. 图象可由直线y=-2x向下平移3个单位长度得到
5 (2024南通崇川月考)已知直线y=kx+b经过第一、三、四象限,则直线y=bx+k一定不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
6 (2024无锡月考)在一次函数y=(a-1)x-3的图象中,y随x的增大而减小,则a的取值范围是 .
7 已知函数y=3+(m-2)xm2-3是一次函数,则m= ,此函数图象经过第 象限.
8 (2025扬州邗江期末)直线y=4x+2沿x轴向右平移2个单位长度,则平移后的直线与x轴,y轴所围成的三角形面积为 .
9 已知点A(x1,y1),B(x2,y2)在函数y=|2x+5|的图象上,x1+x2=m,且当x1<x2时,都有y1<y2,则m的取值范围为 .
10 (2024常州天宁月考)若直线y=ax+b过点(0,2),且与坐标轴围成的图形是等腰直角三角形,则a的值为 .
11 (2025宿迁泗洪二模)已知一次函数y=-x+5,将其图象绕y轴上的点P(0,a)旋转180°,所得的图象经过点(0,-3),则a的值为 .
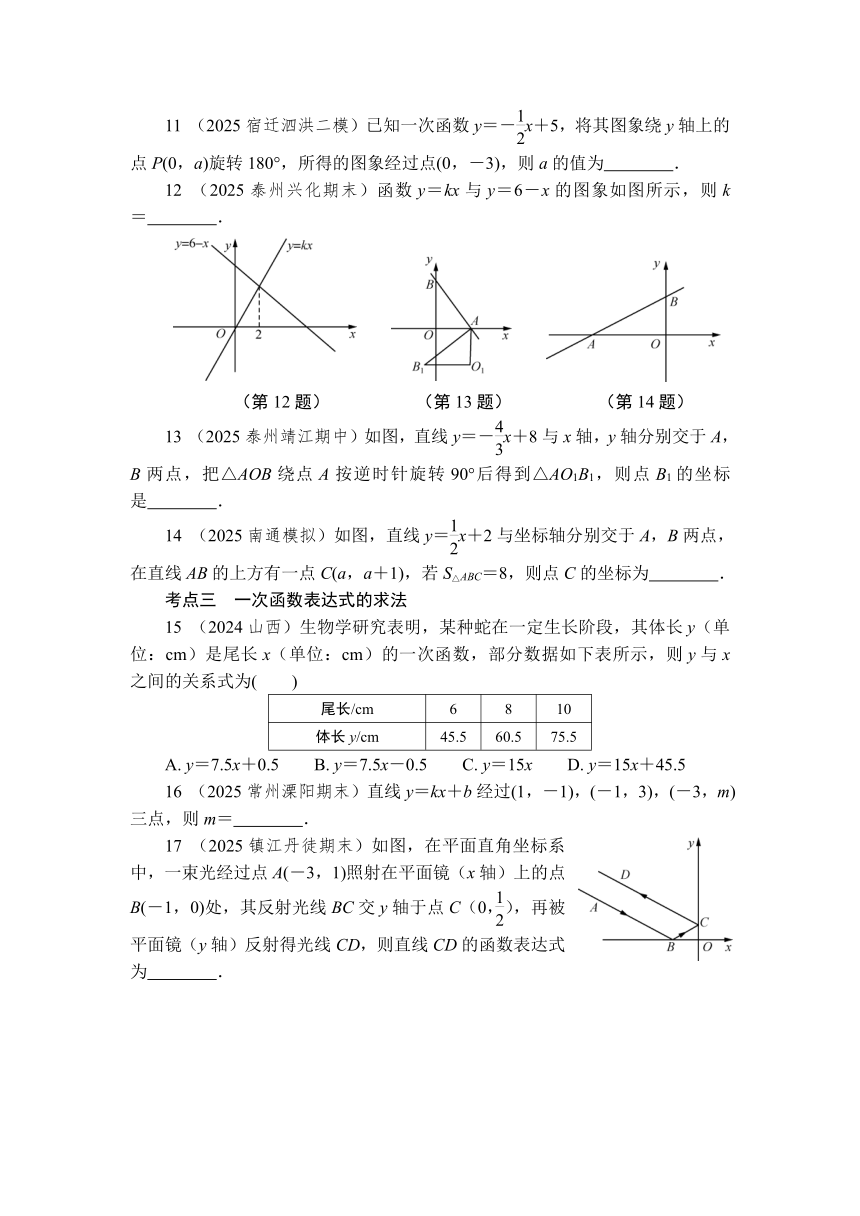
12 (2025泰州兴化期末)函数y=kx与y=6-x的图象如图所示,则k= .
(第12题) (第13题) (第14题)
13 (2025泰州靖江期中)如图,直线y=-x+8与x轴,y轴分别交于A,B两点,把△AOB绕点A按逆时针旋转90°后得到△AO1B1,则点B1的坐标是 .
14 (2025南通模拟)如图,直线y=x+2与坐标轴分别交于A,B两点,在直线AB的上方有一点C(a,a+1),若S△ABC=8,则点C的坐标为 .
考点三 一次函数表达式的求法
15 (2024山西)生物学研究表明,某种蛇在一定生长阶段,其体长y(单位:cm)是尾长x(单位:cm)的一次函数,部分数据如下表所示,则y与x之间的关系式为( )
尾长/cm 6 8 10
体长y/cm 45.5 60.5 75.5
A. y=7.5x+0.5 B. y=7.5x-0.5 C. y=15x D. y=15x+45.5
16 (2025常州溧阳期末)直线y=kx+b经过(1,-1),(-1,3),(-3,m)三点,则m= .
17 (2025镇江丹徒期末)如图,在平面直角坐标系中,一束光经过点A(-3,1)照射在平面镜(x轴)上的点B(-1,0)处,其反射光线BC交y轴于点C(0,),再被平面镜(y轴)反射得光线CD,则直线CD的函数表达式为 .
18 (2024北京)在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y=-kx+3的图象交于点(2,1).
(1) 求k,b的值;
(2) 当x>2时,对于x的每一个值,函数y=mx(m≠0)的值既大于函数y=kx+b的值,也大于函数y=-kx+3的值,直接写出m的取值范围.
考点四 一次函数与二元一次方程
19 (2025扬州期末)若直线y=3x+a与直线y=-x的交点的横坐标为2,则关于x,y的二元一次方程组的解是( )
A. B.
C. D.
20 (2024泰州泰兴期末)一次函数y=mx+n的图象如图所示,则关于x的方程mx+n-3=0的解是 .
考点五 一次函数的应用
21 因活动需要购买某种水果,数学活动小组的同学通过市场调查得知,在甲商店购买该水果的费用y1(单位:元)与该水果的质量x(单位:kg)之间的关系如图所示;在乙商店购买该水果的费用y2(单位:元)与该水果的质量x(单位:kg)之间的函数表达式为y2=10x(x≥0).
(1) 求y1与x之间的函数表达式;
(2) 现计划用600元购买该水果,选甲、乙哪家商店能购买该水果更多一些?
22 2023年7月28日至8月8日,第31届世界大学生运动会将在成都举行.为了响应“当好东道主,热情迎嘉宾”的号召,成都某知名小吃店计划购买A,B两种食材制作小吃.已知购买A种食材1 kg和B种食材1 kg共需68元,购买A种食材5 kg和B种食材3 kg共需280元.
(1) 求A,B两种食材的单价;
(2) 该小吃店计划购买两种食材共36 kg,其中购买A种食材的千克数不少于B种食材的千克数的2倍,当A,B两种食材分别购买多少千克时,总费用最少?并求出最少总费用.
期末专题训练(五) 一 次 函 数
1. B 2. C 3. D 4. C 5. C 6. a<1 7. -2 一、二、四
8. 9. m>-5 10. ±1 11. 1 12. 2 13. (-2,-6)
14. (10,11) 15. A 16. 7 17. y=-0.5x+0.5
18. 解:(1) 因为直线y=-kx+3经过点(2,1),
所以-2k+3=1,
解得k=1,
将点(2,1)代入y=x+b,得2+b=1,
解得b=-1.
(2) m≥1
19. D 20. x=0
21. 解:(1) 当0≤x≤5时,设y1与x之间的函数表达式为y1=kx(k≠0),
把(5,75)代入表达式,得5k=75,解得k=15,
所以y1=15x.
当x>5时,设y1与x之间的函数表达式为y1=mx+n(m≠0),
把(5,75)和(10,120)代入表达式,
得解得
所以y1=9x+30.
综上所述,y1与x之间的函数表达式为
y1=
(2) 令9x+30=600,解得x=,
所以在甲商店用600元可以购买 kg水果.
令10x=600,解得x=60,
所以在乙商店用600元可以购买60 kg水果.
因为>60,
所以在甲商店购买该水果更多一些.
22. 解:(1) 设A种食材的单价为x元/kg,B种食材的单价为y元/kg,
由题意,得解得
所以A种食材的单价是38元/kg,B种食材的单价是30元/kg.
(2) 设A种食材购买m kg,B种食材购买(36-m)kg,总费用为w元,
由题意,得w=38m+30(36-m)=8m+1 080,
因为m≥2(36-m),所以24≤m<36,
因为w随m的增大而增大,
所以当m=24时,w有最小值为8×24+1 080=1 272,
所以A种食材购买24 kg,B种食材购买12 kg时,总费用最少,为1 272元.
考点一 变量与函数
1 (2024南通崇川月考)下列曲线中,不能表示y是x的函数的是( )
A B C D
2 (2024江西)将常温中的温度计插入一杯60 ℃的热水(恒温)中,温度计的读数y(单位:℃)与时间x(单位:min)的关系用图象可近似表示为( )
A B D C
考点二 正比例函数与一次函数的图象与性质
3 (2025苏州模拟)若点(3,-4)在正比例函数y=kx(k≠0)的图象上,则k的值为( )
A. -12 B. 12 C. - D. -
4 (2024扬州邗江期末)对于一次函数y=-2x-3,下列说法中不正确的是( )
A. 图象不经过第一象限
B. 图象与y轴的交点坐标为(0,-3)
C. 若点(-1,y1),(4,y2)在一次函数y=-2x-3的图象上,则y1<y2
D. 图象可由直线y=-2x向下平移3个单位长度得到
5 (2024南通崇川月考)已知直线y=kx+b经过第一、三、四象限,则直线y=bx+k一定不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
6 (2024无锡月考)在一次函数y=(a-1)x-3的图象中,y随x的增大而减小,则a的取值范围是 .
7 已知函数y=3+(m-2)xm2-3是一次函数,则m= ,此函数图象经过第 象限.
8 (2025扬州邗江期末)直线y=4x+2沿x轴向右平移2个单位长度,则平移后的直线与x轴,y轴所围成的三角形面积为 .
9 已知点A(x1,y1),B(x2,y2)在函数y=|2x+5|的图象上,x1+x2=m,且当x1<x2时,都有y1<y2,则m的取值范围为 .
10 (2024常州天宁月考)若直线y=ax+b过点(0,2),且与坐标轴围成的图形是等腰直角三角形,则a的值为 .
11 (2025宿迁泗洪二模)已知一次函数y=-x+5,将其图象绕y轴上的点P(0,a)旋转180°,所得的图象经过点(0,-3),则a的值为 .
12 (2025泰州兴化期末)函数y=kx与y=6-x的图象如图所示,则k= .
(第12题) (第13题) (第14题)
13 (2025泰州靖江期中)如图,直线y=-x+8与x轴,y轴分别交于A,B两点,把△AOB绕点A按逆时针旋转90°后得到△AO1B1,则点B1的坐标是 .
14 (2025南通模拟)如图,直线y=x+2与坐标轴分别交于A,B两点,在直线AB的上方有一点C(a,a+1),若S△ABC=8,则点C的坐标为 .
考点三 一次函数表达式的求法
15 (2024山西)生物学研究表明,某种蛇在一定生长阶段,其体长y(单位:cm)是尾长x(单位:cm)的一次函数,部分数据如下表所示,则y与x之间的关系式为( )
尾长/cm 6 8 10
体长y/cm 45.5 60.5 75.5
A. y=7.5x+0.5 B. y=7.5x-0.5 C. y=15x D. y=15x+45.5
16 (2025常州溧阳期末)直线y=kx+b经过(1,-1),(-1,3),(-3,m)三点,则m= .
17 (2025镇江丹徒期末)如图,在平面直角坐标系中,一束光经过点A(-3,1)照射在平面镜(x轴)上的点B(-1,0)处,其反射光线BC交y轴于点C(0,),再被平面镜(y轴)反射得光线CD,则直线CD的函数表达式为 .
18 (2024北京)在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y=-kx+3的图象交于点(2,1).
(1) 求k,b的值;
(2) 当x>2时,对于x的每一个值,函数y=mx(m≠0)的值既大于函数y=kx+b的值,也大于函数y=-kx+3的值,直接写出m的取值范围.
考点四 一次函数与二元一次方程
19 (2025扬州期末)若直线y=3x+a与直线y=-x的交点的横坐标为2,则关于x,y的二元一次方程组的解是( )
A. B.
C. D.
20 (2024泰州泰兴期末)一次函数y=mx+n的图象如图所示,则关于x的方程mx+n-3=0的解是 .
考点五 一次函数的应用
21 因活动需要购买某种水果,数学活动小组的同学通过市场调查得知,在甲商店购买该水果的费用y1(单位:元)与该水果的质量x(单位:kg)之间的关系如图所示;在乙商店购买该水果的费用y2(单位:元)与该水果的质量x(单位:kg)之间的函数表达式为y2=10x(x≥0).
(1) 求y1与x之间的函数表达式;
(2) 现计划用600元购买该水果,选甲、乙哪家商店能购买该水果更多一些?
22 2023年7月28日至8月8日,第31届世界大学生运动会将在成都举行.为了响应“当好东道主,热情迎嘉宾”的号召,成都某知名小吃店计划购买A,B两种食材制作小吃.已知购买A种食材1 kg和B种食材1 kg共需68元,购买A种食材5 kg和B种食材3 kg共需280元.
(1) 求A,B两种食材的单价;
(2) 该小吃店计划购买两种食材共36 kg,其中购买A种食材的千克数不少于B种食材的千克数的2倍,当A,B两种食材分别购买多少千克时,总费用最少?并求出最少总费用.
期末专题训练(五) 一 次 函 数
1. B 2. C 3. D 4. C 5. C 6. a<1 7. -2 一、二、四
8. 9. m>-5 10. ±1 11. 1 12. 2 13. (-2,-6)
14. (10,11) 15. A 16. 7 17. y=-0.5x+0.5
18. 解:(1) 因为直线y=-kx+3经过点(2,1),
所以-2k+3=1,
解得k=1,
将点(2,1)代入y=x+b,得2+b=1,
解得b=-1.
(2) m≥1
19. D 20. x=0
21. 解:(1) 当0≤x≤5时,设y1与x之间的函数表达式为y1=kx(k≠0),
把(5,75)代入表达式,得5k=75,解得k=15,
所以y1=15x.
当x>5时,设y1与x之间的函数表达式为y1=mx+n(m≠0),
把(5,75)和(10,120)代入表达式,
得解得
所以y1=9x+30.
综上所述,y1与x之间的函数表达式为
y1=
(2) 令9x+30=600,解得x=,
所以在甲商店用600元可以购买 kg水果.
令10x=600,解得x=60,
所以在乙商店用600元可以购买60 kg水果.
因为>60,
所以在甲商店购买该水果更多一些.
22. 解:(1) 设A种食材的单价为x元/kg,B种食材的单价为y元/kg,
由题意,得解得
所以A种食材的单价是38元/kg,B种食材的单价是30元/kg.
(2) 设A种食材购买m kg,B种食材购买(36-m)kg,总费用为w元,
由题意,得w=38m+30(36-m)=8m+1 080,
因为m≥2(36-m),所以24≤m<36,
因为w随m的增大而增大,
所以当m=24时,w有最小值为8×24+1 080=1 272,
所以A种食材购买24 kg,B种食材购买12 kg时,总费用最少,为1 272元.
同课章节目录
