期末专题训练(一) 三角形 同步练(含答案) 2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 期末专题训练(一) 三角形 同步练(含答案) 2025-2026学年数学苏科版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 191.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 21:40:47 | ||
图片预览

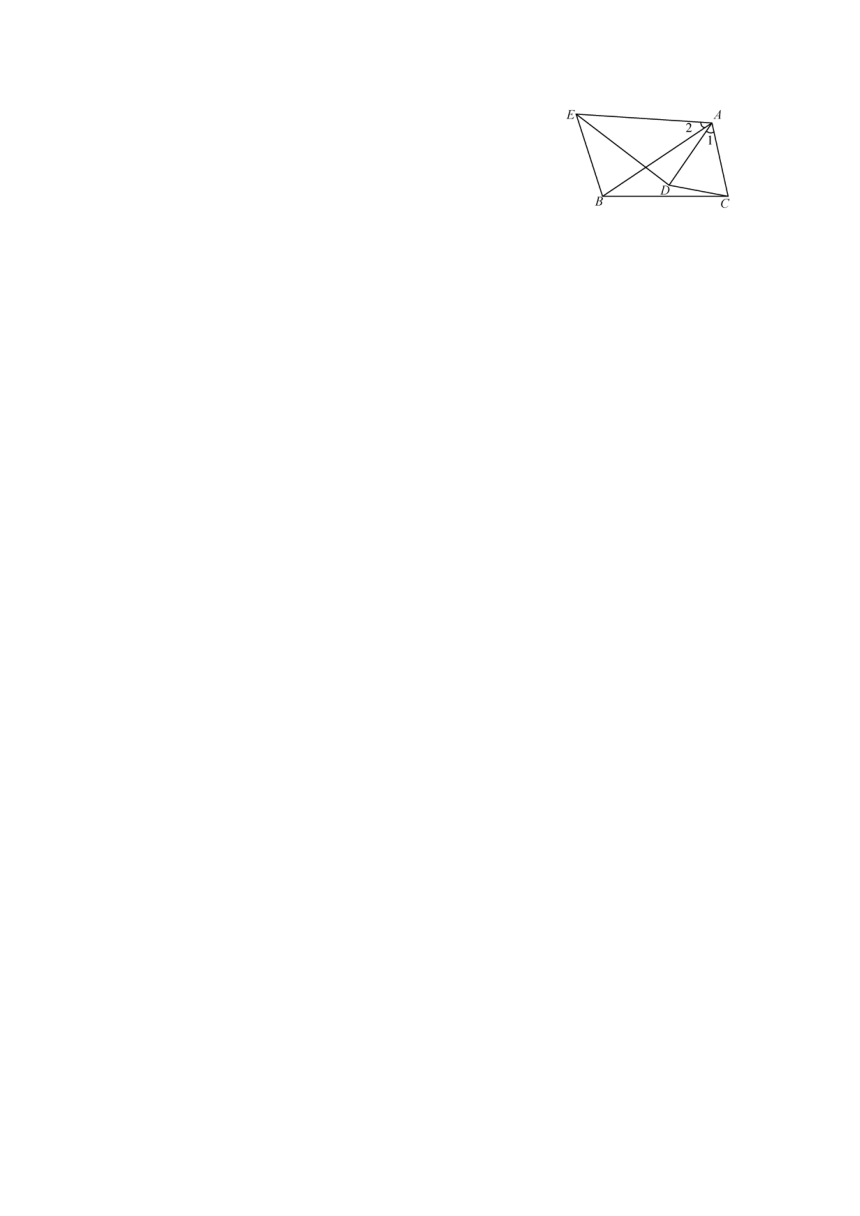

文档简介
期末专题训练
专题训练(一) 三 角 形
考点一 三角形三边关系
1 (2025宿迁泗洪二模)已知某三角形的三边长分别为3,7,m,则m的值可以是( )
A. 1 B. 4 C. 7 D. 10
2 (2025连云港期末)利用数形结合的思想,可以比较实数的大小.若在方格纸中构造如图所示的图形(方格纸中每个小方格的边长为1),结合图形可得
1+.(填“>”“<”或“=”)
(第2题) (第3题) (第4题) (第5题) (第6题)
考点二 三角形中的重要线段
3 (2024扬州江都期末)如图,D,E分别是△ABC中边AB,BC上的点,AD=BD,BE=2CE,AE与CD相交于点F.若四边形BEFD的面积为10,则△ABC的面积为( )
A. 18 B. 20 C. 22 D. 24
4 (2025泰州期末) 如图,在△ABC中,AD,AE分别是边BC上的高和中线.若AD=5,BE=4,则△AEC的面积是 .
考点三 全等三角形的性质与判定
5 (2025盐城一模)如图,点B,C,D在同一直线上,若△ABC≌△CDE,AB=9,BD=14,则BC的长为( )
A. 9 B. 4 C. 5 D. 6
6 (2024镇江句容期末)如图,∠1=∠2,AE=AC,要使△ADE≌△ABC,则可添加的一个条件是 W.(写出一个即可)
7 (2025苏州相城月考)如图,在等腰三角形ACD和等腰三角形AEB中,AC=AD,AE=AB,且∠1=∠2.
(1) 求证:ED=BC;
(2) 若∠2=50°,∠BCD=10°,试计算∠ADE的大小.
考点四 垂直平分线的性质、角平分线
8 (2025镇江丹徒一模)如图,在△ABC中,∠ABC的平分线与BC的垂直平分线交于点D,连接CD.若∠A=70°,∠ABC=60°,则∠ACD= .
(第8题) (第9题)(第11题) (第13题) (第14题)
9 如图,线段AB的垂直平分线与线段BC的垂直平分线的交点P恰好在AC上,且AC=10 cm,则点P到点B的距离为 cm.
10 (2025苏州虎丘月考)如图,在△ABC中,∠BAC>90°,AB的垂直平分线分别交AB,BC于点E,F,AC的垂直平分线分别交AC,BC于点M,N,直线EF,MN相交于点P.
(1) 求证:点P在线段BC的垂直平分线上;
(2) 已知∠FAN=56°,求∠FPN的度数.
考点五 等腰三角形的性质与判定
11 (2024常州钟楼期中)如图,在Rt△ABC中,∠C=90°,∠A=30°.若某个三角形与△ABC能拼成一个等腰三角形(无重叠),则拼成的等腰三角形有( )
A. 4种 B. 5种 C. 6种 D. 7种
12 等腰三角形一腰上的高与另一腰的夹角为45°,则其顶角为 .
13 (2025扬州期末)如图,点C,E在OA上,点D在OB上,且OC=CD=DE,若∠EDB=75°,则∠AOB= .
14 如图,在等腰三角形ABC中,AB=AC,∠A=50°,直线MN垂直平分边AC,分别交AB,AC于点D,E,则∠BCD的度数为 .
15 如图,在△ABC中,边AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.
(1) 求证:AD⊥BC.
(2) 若∠BAC=75°,求∠B的度数.
考点六 等边三角形的性质与判定
16 如图,等边三角形纸片ABC的边长为8,点E,F是边BC上的三等分点,分别过点E,F沿着平行于BA,CA的方向各剪一刀,则剪下的△DEF的周长是( )
A. 3 B. C. 6 D. 8
(第16题) (第17题)
17 (2024常州梁溪月考)如图,已知等边三角形ABC纸片,点E在边AC上,点F在边AB上,沿EF折叠,使点A落在边BC上点D的位置,且ED⊥BC,则∠EFD= .
18 (2025苏州吴江月考)如图,在△ABC中,AB=AC,∠ACB>60°,在边AC上取点D,使BD=BC.以AD为一边作等边三角形ADE,且使点E与点B位于直线AC的同侧.
(1) 若点D与点E关于直线AB轴对称,求∠BDE的度数;
(2) 若∠ACB=80°,写出线段BA,BD,BE之间的数量关系,并说明理由.
考点七 直角三角形的性质
19 (2025南通海门月考)如图,在Rt△ABC中,∠BAC=90°,AD,AE分别是边BC上的中线和高,若AE=2,S△ABD=,则AD的长为( )
A. B. C. 1 D.
(第19题) (第20题)
20 (2024徐州沛县期末)如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD.若∠BAD=56°,则∠EDB的度数为 .
期末专题训练
专题训练(一) 三 角 形
1. C 2. < 3. D 4. 10 5. C
6. AD=AB(答案不唯一)
7. (1) 证明:因为∠1=∠2,
所以∠1+∠BAD=∠2+∠BAD,
所以∠BAC=∠EAD.
在△EAD和△BAC中,
所以△EAD≌△BAC(SAS),
所以ED=BC.
(2) 解:因为AC=AD,∠1=∠2=50°,∠BCD=10°,
所以∠ADC=∠ACD.
因为∠ADC+∠ACD+∠1=180°,
所以2∠ACD+50°=180°,
所以∠ACD=65°,
所以∠ACB=∠ACD+∠BCD=65°+10°=75°,
由(1)可得△EAD≌△BAC,
所以∠ADE=∠ACB=75°,
所以∠ADE的度数是75°.
8. 20° 9. 5
10. (1) 证明:连接BP,AP,PC.
因为PE垂直平分线段AB,PM垂直平分线段AC,
所以PA=PB,PA=PC,
所以PB=PC,
所以点P在线段BC的垂直平分线上.
(2) 解:因为PE垂直平分线段AB,PM垂直平分线段AC,
所以FA=FB,NA=NC,∠AEP=∠AMP=∠BEF=∠CMN=90°,
所以∠ABC+∠BFE=∠ACB+∠MNC=90°.
设∠ABC=x,∠ACB=y,
所以∠ABC=∠BAF=x,∠ACB=∠CAN=y,∠BFE=90°-x,∠MNC=90°-y,
所以∠PFN=∠BFE=90°-x,∠PNF=∠MNC=90°-y.
因为∠ABC+∠ACB+∠CAB=180°,∠FAN=56°,
所以2x+2y+56°=180°,
则2(x+y)=124°,
解得x+y=62°.
因为∠PFN+∠PNF+∠FPN=180°,
所以90°-x+90°-y+∠FPN=180°,
所以∠FPN=180°-180°+(x+y)=62°.
11. B 12. 45°或135° 13. 25° 14. 15°
15. (1) 证明:如图,连接AE.
因为EF垂直平分线段AB,
所以AE=BE.
因为BE=AC,
所以AE=AC.
因为D是线段EC的中点,
所以AD⊥BC.
(2) 解:设∠B=x.
因为AE=BE,
所以∠BAE=∠B=x,
所以由三角形的外角的性质,得∠AEC=2x.
因为AE=AC,
所以∠C=∠AEC=2x,
在△ABC中,3x+75°=180°,解得x=35°,
所以∠B=35°.
16. D 17. 45°
18. 解:(1) 因为△ADE是等边三角形,
所以∠ADE=∠EAD=60°.
因为点D与点E关于直线AB轴对称,
所以∠EAB=∠DAB=∠EAD=30°.
因为AB=AC,
所以∠C=∠ABC=(180°-∠BAC)=75°.
因为BD=BC,
所以∠BDC=∠C=75°,
所以∠ADB=180°-∠BDC=105°,
所以∠BDE=∠ADB-∠ADE=45°.
(2) BA=BD+BE.理由如下:
在AB上取点F,使BF=BD,连接DF,BE,
又∠ACB=80°,AB=AC,
所以∠ABC=∠ACB=80°.
因为BD=BC,
所以∠BDC=∠BCD=80°,
所以∠CBD=20°,
所以∠DBF=60°,
所以△BDF是等边三角形.
又因为△ADE是等边三角形,
所以∠BDF=∠ADE=60°,BD=DF,DE=DA,
所以∠BDE=∠ADF,
所以△BDE≌△FDA(SAS),
所以BE=FA.
又因为AB=AF+BF,
所以BA=BD+BE.
19. A 20. 34°
专题训练(一) 三 角 形
考点一 三角形三边关系
1 (2025宿迁泗洪二模)已知某三角形的三边长分别为3,7,m,则m的值可以是( )
A. 1 B. 4 C. 7 D. 10
2 (2025连云港期末)利用数形结合的思想,可以比较实数的大小.若在方格纸中构造如图所示的图形(方格纸中每个小方格的边长为1),结合图形可得
1+.(填“>”“<”或“=”)
(第2题) (第3题) (第4题) (第5题) (第6题)
考点二 三角形中的重要线段
3 (2024扬州江都期末)如图,D,E分别是△ABC中边AB,BC上的点,AD=BD,BE=2CE,AE与CD相交于点F.若四边形BEFD的面积为10,则△ABC的面积为( )
A. 18 B. 20 C. 22 D. 24
4 (2025泰州期末) 如图,在△ABC中,AD,AE分别是边BC上的高和中线.若AD=5,BE=4,则△AEC的面积是 .
考点三 全等三角形的性质与判定
5 (2025盐城一模)如图,点B,C,D在同一直线上,若△ABC≌△CDE,AB=9,BD=14,则BC的长为( )
A. 9 B. 4 C. 5 D. 6
6 (2024镇江句容期末)如图,∠1=∠2,AE=AC,要使△ADE≌△ABC,则可添加的一个条件是 W.(写出一个即可)
7 (2025苏州相城月考)如图,在等腰三角形ACD和等腰三角形AEB中,AC=AD,AE=AB,且∠1=∠2.
(1) 求证:ED=BC;
(2) 若∠2=50°,∠BCD=10°,试计算∠ADE的大小.
考点四 垂直平分线的性质、角平分线
8 (2025镇江丹徒一模)如图,在△ABC中,∠ABC的平分线与BC的垂直平分线交于点D,连接CD.若∠A=70°,∠ABC=60°,则∠ACD= .
(第8题) (第9题)(第11题) (第13题) (第14题)
9 如图,线段AB的垂直平分线与线段BC的垂直平分线的交点P恰好在AC上,且AC=10 cm,则点P到点B的距离为 cm.
10 (2025苏州虎丘月考)如图,在△ABC中,∠BAC>90°,AB的垂直平分线分别交AB,BC于点E,F,AC的垂直平分线分别交AC,BC于点M,N,直线EF,MN相交于点P.
(1) 求证:点P在线段BC的垂直平分线上;
(2) 已知∠FAN=56°,求∠FPN的度数.
考点五 等腰三角形的性质与判定
11 (2024常州钟楼期中)如图,在Rt△ABC中,∠C=90°,∠A=30°.若某个三角形与△ABC能拼成一个等腰三角形(无重叠),则拼成的等腰三角形有( )
A. 4种 B. 5种 C. 6种 D. 7种
12 等腰三角形一腰上的高与另一腰的夹角为45°,则其顶角为 .
13 (2025扬州期末)如图,点C,E在OA上,点D在OB上,且OC=CD=DE,若∠EDB=75°,则∠AOB= .
14 如图,在等腰三角形ABC中,AB=AC,∠A=50°,直线MN垂直平分边AC,分别交AB,AC于点D,E,则∠BCD的度数为 .
15 如图,在△ABC中,边AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.
(1) 求证:AD⊥BC.
(2) 若∠BAC=75°,求∠B的度数.
考点六 等边三角形的性质与判定
16 如图,等边三角形纸片ABC的边长为8,点E,F是边BC上的三等分点,分别过点E,F沿着平行于BA,CA的方向各剪一刀,则剪下的△DEF的周长是( )
A. 3 B. C. 6 D. 8
(第16题) (第17题)
17 (2024常州梁溪月考)如图,已知等边三角形ABC纸片,点E在边AC上,点F在边AB上,沿EF折叠,使点A落在边BC上点D的位置,且ED⊥BC,则∠EFD= .
18 (2025苏州吴江月考)如图,在△ABC中,AB=AC,∠ACB>60°,在边AC上取点D,使BD=BC.以AD为一边作等边三角形ADE,且使点E与点B位于直线AC的同侧.
(1) 若点D与点E关于直线AB轴对称,求∠BDE的度数;
(2) 若∠ACB=80°,写出线段BA,BD,BE之间的数量关系,并说明理由.
考点七 直角三角形的性质
19 (2025南通海门月考)如图,在Rt△ABC中,∠BAC=90°,AD,AE分别是边BC上的中线和高,若AE=2,S△ABD=,则AD的长为( )
A. B. C. 1 D.
(第19题) (第20题)
20 (2024徐州沛县期末)如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD.若∠BAD=56°,则∠EDB的度数为 .
期末专题训练
专题训练(一) 三 角 形
1. C 2. < 3. D 4. 10 5. C
6. AD=AB(答案不唯一)
7. (1) 证明:因为∠1=∠2,
所以∠1+∠BAD=∠2+∠BAD,
所以∠BAC=∠EAD.
在△EAD和△BAC中,
所以△EAD≌△BAC(SAS),
所以ED=BC.
(2) 解:因为AC=AD,∠1=∠2=50°,∠BCD=10°,
所以∠ADC=∠ACD.
因为∠ADC+∠ACD+∠1=180°,
所以2∠ACD+50°=180°,
所以∠ACD=65°,
所以∠ACB=∠ACD+∠BCD=65°+10°=75°,
由(1)可得△EAD≌△BAC,
所以∠ADE=∠ACB=75°,
所以∠ADE的度数是75°.
8. 20° 9. 5
10. (1) 证明:连接BP,AP,PC.
因为PE垂直平分线段AB,PM垂直平分线段AC,
所以PA=PB,PA=PC,
所以PB=PC,
所以点P在线段BC的垂直平分线上.
(2) 解:因为PE垂直平分线段AB,PM垂直平分线段AC,
所以FA=FB,NA=NC,∠AEP=∠AMP=∠BEF=∠CMN=90°,
所以∠ABC+∠BFE=∠ACB+∠MNC=90°.
设∠ABC=x,∠ACB=y,
所以∠ABC=∠BAF=x,∠ACB=∠CAN=y,∠BFE=90°-x,∠MNC=90°-y,
所以∠PFN=∠BFE=90°-x,∠PNF=∠MNC=90°-y.
因为∠ABC+∠ACB+∠CAB=180°,∠FAN=56°,
所以2x+2y+56°=180°,
则2(x+y)=124°,
解得x+y=62°.
因为∠PFN+∠PNF+∠FPN=180°,
所以90°-x+90°-y+∠FPN=180°,
所以∠FPN=180°-180°+(x+y)=62°.
11. B 12. 45°或135° 13. 25° 14. 15°
15. (1) 证明:如图,连接AE.
因为EF垂直平分线段AB,
所以AE=BE.
因为BE=AC,
所以AE=AC.
因为D是线段EC的中点,
所以AD⊥BC.
(2) 解:设∠B=x.
因为AE=BE,
所以∠BAE=∠B=x,
所以由三角形的外角的性质,得∠AEC=2x.
因为AE=AC,
所以∠C=∠AEC=2x,
在△ABC中,3x+75°=180°,解得x=35°,
所以∠B=35°.
16. D 17. 45°
18. 解:(1) 因为△ADE是等边三角形,
所以∠ADE=∠EAD=60°.
因为点D与点E关于直线AB轴对称,
所以∠EAB=∠DAB=∠EAD=30°.
因为AB=AC,
所以∠C=∠ABC=(180°-∠BAC)=75°.
因为BD=BC,
所以∠BDC=∠C=75°,
所以∠ADB=180°-∠BDC=105°,
所以∠BDE=∠ADB-∠ADE=45°.
(2) BA=BD+BE.理由如下:
在AB上取点F,使BF=BD,连接DF,BE,
又∠ACB=80°,AB=AC,
所以∠ABC=∠ACB=80°.
因为BD=BC,
所以∠BDC=∠BCD=80°,
所以∠CBD=20°,
所以∠DBF=60°,
所以△BDF是等边三角形.
又因为△ADE是等边三角形,
所以∠BDF=∠ADE=60°,BD=DF,DE=DA,
所以∠BDE=∠ADF,
所以△BDE≌△FDA(SAS),
所以BE=FA.
又因为AB=AF+BF,
所以BA=BD+BE.
19. A 20. 34°
同课章节目录
