期末综合测试卷A 同步练 2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 期末综合测试卷A 同步练 2025-2026学年数学苏科版(2024)八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 260.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 00:00:00 | ||
图片预览



文档简介
期末综合测试卷A
(时间:120分钟 满分:150分)
一、 选择题(每小题3分,共24分)
1. (2025东台期末)在平面直角坐标系中,点P(4,-2)所在的象限为( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 如图,已知CD=CA,∠D=∠A,添加下列条件仍不能证明△DEC≌△ABC的是( )
A. ∠DEC=∠B B. ∠ACD=∠BCE C. CE=CB D. DE=AB
图1 图2
(第2题) (第7题) (第8题)
3. (2024扬州宝应期末)下列结论中,正确的是( )
A. 81的立方根是3 B. 的平方根是±4
C. 立方根等于平方根的数是1 D. 4的算术平方根是2
4. 下列各组数中,是勾股数的是( )
A. 12,15,18 B. 6,8,12 C. 4,5,6 D. 7,24,25
5. 关于直线l:y=kx+k(k≠0),下列说法中不正确的是( )
A. 点(0,k)在直线l上 B. 直线l经过定点(-1,0)
C. 当k>0时,y随x的增大而增大 D. 直线l经过第一、二、三象限
6. (2024常州溧阳期末)已知点A(,m),B(2,n)在一次函数y=ax+b(a>0)的图象上,则m与n的大小关系是( )
A. m>n B. m=n C. m<n D. 无法确定
7. (2024南京鼓楼期末)如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,点A在ED上.若AE=1,AD=3,则BC的长为( )
A. B. C. 2.5 D. 2
8. 如图1(图中各角均为直角),动点P从点A出发,以每秒1个单位长度的速度沿A→B→C→D→E路线匀速运动,△AFP的面积 y与点P运动的时间x(s)之间的函数关系图象如图2所示,则CD的长为( )
A. 5 B. 6 C. 7 D. 8
二、 填空题(每小题3分,共30分)
9. 36的平方根是 .
10. -π的绝对值是 .
11. 点A(3,5)关于x轴对称的点的坐标是 .
12. 已知点P(m-2,2m-1)在第二象限,则实数m的取值范围是 .
13. 已知a-1的平方根是±2,b+1的立方根为2,则代数式的值为 .
14. (2024南京鼓楼期末)如图,一架2.5 m长的梯子AB,斜靠在竖直的墙AC上,这时梯子的底部B到墙底端C的距离为1.5 m,则梯子的顶端距离地面为 m.
(第14题) (第15题) (第16题) (第17题) (第18题)
15. 如图,在平面直角坐标系中,点A的坐标为(-6,0),线段AB向右平移4个单位长度到线段CD,线段CD与y轴交于点E,若△CEO的面积为4,则点E的坐标为 .
16. 如图,直线l1:y=-x+m与x轴交于点A,直线l2:y=2x+n与y轴交于点B,与直线l1交于点P(2,2),则△PAB的面积为 .
17. 如图,在Rt△ABC中,∠C=90°,AB=5 cm,AC=3 cm,动点P从点B出发,沿射线BC以2 cm/s的速度移动,设运动的时间为t s,则当t= 时,△ABP为直角三角形.
18. (2024苏州姑苏期末)如图,△ABC的三个顶点坐标分别为A(-6,0),B(0,8),C(9,0),M是线段OB上的一点,连接AM并延长交BC于点N.若AM平分∠BAC,则点N的坐标是 .
三、 解答题(共96分)
19. (10分)(2025泰州姜堰期末)(1) 计算:()2+-;
(2) 已知(x+1)3+1=0,求x的值.
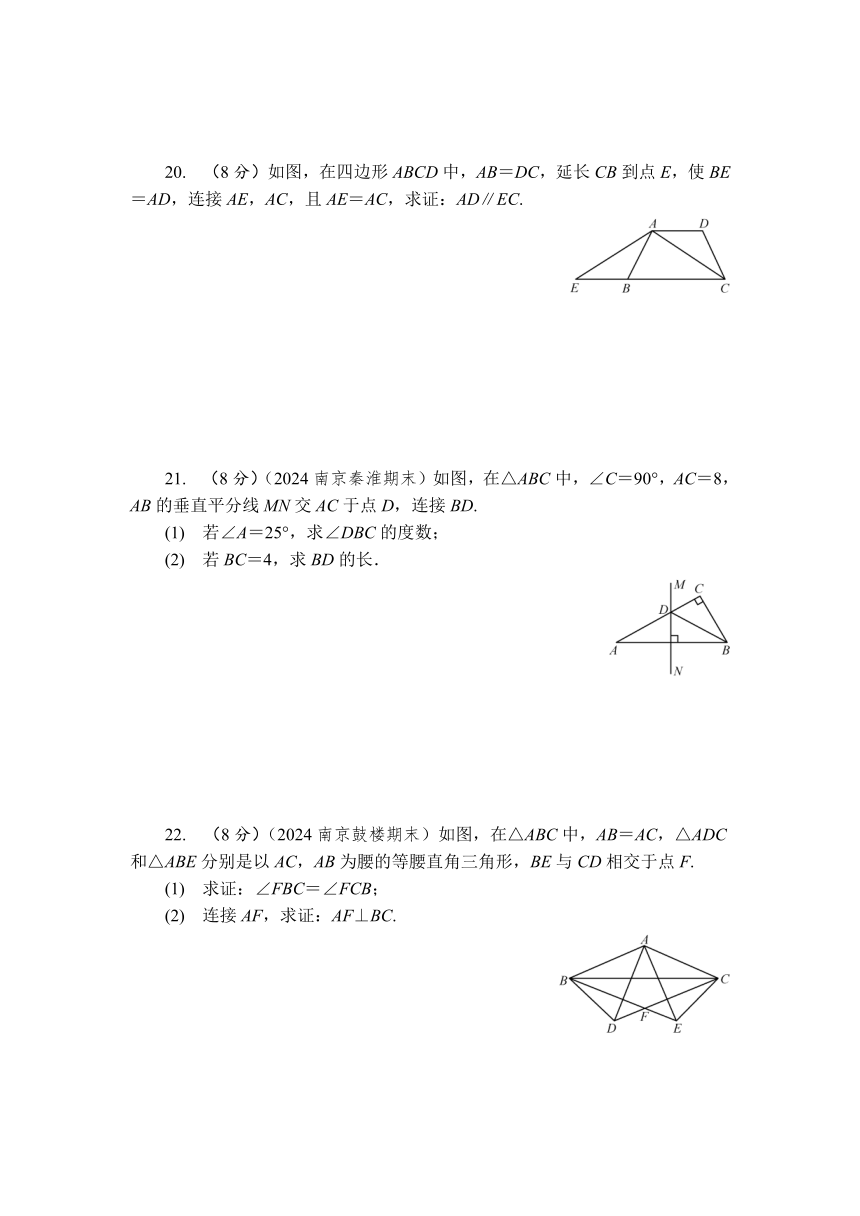
20. (8分)如图,在四边形ABCD中,AB=DC,延长CB到点E,使BE=AD,连接AE,AC,且AE=AC,求证:AD∥EC.
21. (8分)(2024南京秦淮期末)如图,在△ABC中,∠C=90°,AC=8,AB的垂直平分线MN交AC于点D,连接BD.
(1) 若∠A=25°,求∠DBC的度数;
(2) 若BC=4,求BD的长.
22. (8分)(2024南京鼓楼期末)如图,在△ABC中,AB=AC,△ADC和△ABE分别是以AC,AB为腰的等腰直角三角形,BE与CD相交于点F.
(1) 求证:∠FBC=∠FCB;
(2) 连接AF,求证:AF⊥BC.
23. (8分)如图,已知直线y=kx+b经过点A(5,0),B(1,4).
(1) 求直线AB的函数表达式;
(2) 若直线y=2x-4与直线AB相交于点C,求点C的坐标;
(3) 根据图象,写出关于x的不等式2x-4>kx+b的解集.
24. (10分)如图,在△ABC中,∠ACB,∠ABC的平分线l1,l2相交于点O.
(1) 求证:点O在∠BAC的平分线上;
(2) 连接OA,若AB=AC=5,OB=4,OA=2,求点O到边BC的距离.
25. (10分)某小区为了绿化环境,计划分两次购进A,B两种树苗,第一次购进A种树苗30棵,B种树苗15棵,共花费1 350元;第二次购进A种树苗24棵,B种树苗10棵,共花费1 060元(两次购进的A,B两种树苗各自的单价均不变).
(1) A,B两种树苗每棵的价格分别是多少元?
(2) 若购买A,B两种树苗共42棵,总费用为W元,购买A种树苗t棵,B种树苗的数量不超过A种树苗数量的2倍.求W与t的函数关系式.请设计出最省钱的购买方案,并求出此方案的总费用.
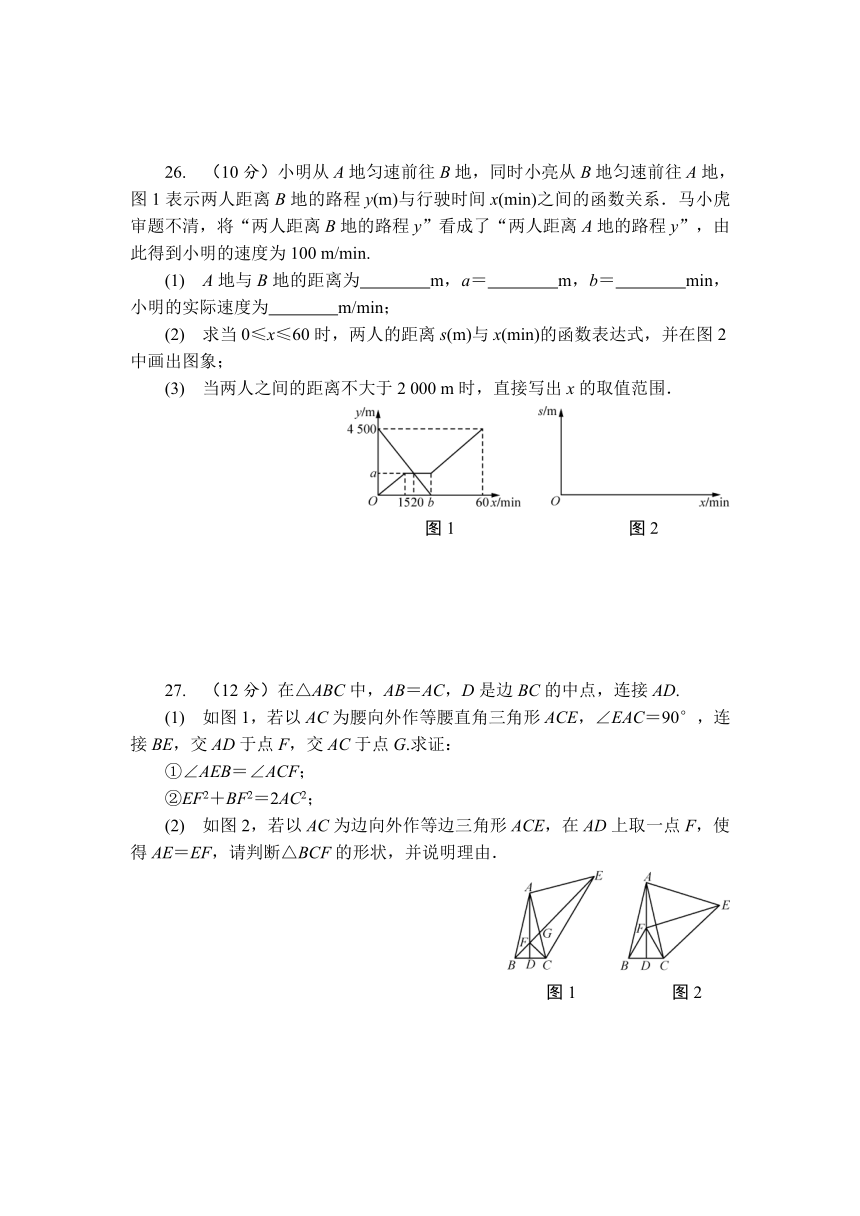
26. (10分)小明从A地匀速前往B地,同时小亮从B地匀速前往A地,图1表示两人距离B地的路程y(m)与行驶时间x(min)之间的函数关系.马小虎审题不清,将“两人距离B地的路程y”看成了“两人距离A地的路程y”,由此得到小明的速度为100 m/min.
(1) A地与B地的距离为 m,a= m,b= min,小明的实际速度为 m/min;
(2) 求当0≤x≤60时,两人的距离s(m)与x(min)的函数表达式,并在图2中画出图象;
(3) 当两人之间的距离不大于2 000 m时,直接写出x的取值范围.
图1 图2
27. (12分)在△ABC中,AB=AC,D是边BC的中点,连接AD.
(1) 如图1,若以AC为腰向外作等腰直角三角形ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.求证:
①∠AEB=∠ACF;
②EF2+BF2=2AC2;
(2) 如图2,若以AC为边向外作等边三角形ACE,在AD上取一点F,使得AE=EF,请判断△BCF的形状,并说明理由.
图1 图2
28. (12分)(2025泰州兴化期末)
【问题导入】
如图1,在直线l上找一点P,如何使得PA+PB最小?
图1 图2
小华同学的思路:作点A关于直线l的对称点A′,连接BA′,与直线l交于点P.由对称可得PA′=PA,所以PA+PB=PA′+PB≥A′B,当且仅当A′,P,B三点共线时,PA′+PB=A′B,此时PA+PB最小.
如图2,在直线l上找一点P,如何使得|PA-PB|最大?
小明同学的思路:作点A关于直线l的对称点A′,连接BA′并延长交直线l于点P.由对称可得PA′=PA,所以|PA-PB|=|PA′-PB|≤A′B,当且仅当A′,P,B三点共线时,|PA-PB|=A′B,此时|PA-PB|最大.
可见,解此类问题的关键是将问题转化为“两点之间线段最短”来解决.
【理解运用】
(1) 如图3,直线y=x+b上有点A(4,a),B(-2,1),点P在x轴上运动,点Q在直线AB下方的y轴上运动.
①求a,b的值;
②当PA+PB最小时,求点P的坐标;
③令t=QA-QB-PA-PB,当t的值最大时,求点Q的坐标及t的最大值;
【深度探究】
(2) 在(1)的条件下,且满足t=QA-QB-PA-PB,当t的值最大时,若M,N分别是线段OP,OQ上的动点,且PM=ON,连接PN,MQ,当PN+MQ最小时,求点M的坐标.
图3 备用图
期末综合测试卷A
1. D 2. C 3. D 4. D 5. D 6. C 7. A 8. B
9. ±6 10. π- 11. (3,-5) 12. <m<2 13.
14. 2 15. (0,4) 16. 10 17. 2或 18. (,)
19. 解:(1) ()2+-
=3+(-4)-2
=-1+(-2)
=-3.
(2) (x+1)3+1=0,
(x+1)3=-1,
x+1=-1,
x=-2.
20. 证明:在△ABE和△CDA中,
所以△ABE≌△CDA(SSS),所以∠E=∠CAD.
因为AE=AC,所以∠E=∠ACE,
所以∠ACE=∠CAD,所以AD∥EC.
21. 解:(1) 因为MN垂直平分AB,
所以DA=DB,所以∠DBA=∠A=25°.
因为∠C=90°,
所以∠ABC=90°-25°=65°,
所以∠DBC=∠ABC-∠DBA=65°-25°=40°.
(2) 设BD=x,则DA=x,所以CD=8-x,
在△BCD中,由勾股定理,得BD2=CD2+BC2,
所以x2=(8-x)2+42,解得x=5,
所以BD=5.
22. 证明:(1) 因为AB=AC,△ADC和△ABE分别是以AC,AB为腰的等腰直角三角形,
所以AD=AE=AB=AC,∠DAC=∠EAB=90°,BE=CD,
所以∠DAB=90°-∠DAE=∠EAC,
所以△ABD≌△ACE(SAS),
所以BD=CE.
因为CD=BE,BC=BC,
所以△BCD≌△CBE(SSS),
所以∠BCD=∠CBE,
即∠FBC=∠FCB.
(2) 由(1)知,BF=FC.
因为AB=AC,
所以AF是BC的垂直平分线,
所以AF⊥BC.
23. 解:(1) 因为直线y=kx+b经过点A(5,0),B(1,4),
所以解得
所以直线AB的函数表达式为y=-x+5.
(2) 若直线y=2x-4与直线AB相交于点C,
则解得
所以点C的坐标为(3,2).
(3) 根据图象可得x>3.
24. (1) 证明:过点O作OD⊥AB,OE⊥AC,OF⊥BC,垂足分别为D,E,F.
因为∠ACB,∠ABC的平分线l1,l2相交于点O,
所以OD=OF,OE=OF,
所以OD=OE,
所以点O在∠BAC的平分线上.
(2) 解:因为AB=AC,AO平分∠BAC,
所以AO⊥BC.
因为OF⊥BC,所以A,O,F三点共线.
设OF=x,则AF=OA+OF=x+2.
在Rt△ABF中,BF2=AB2-AF2,
即BF2=25-(x+2)2,
在Rt△OBF中,BF2=OB2-OF2,
即BF2=16-x2,
所以25-(x+2)2=16-x2,
解得x=,所以OF=,
所以点O到边BC的距离是.
25. 解:(1) 设A种树苗每棵的价格是x元,B种树苗每棵的价格是y元.
根据题意,得解得
所以A种树苗每棵的价格是40元,B种树苗每棵的价格是10元.
(2) 由购买A种树苗的数量为t棵,得购买B种树苗的数量为(42-t)棵.
因为B种树苗的数量不超过A种树苗数量的2倍,
所以42-t≤2t,解得t≥14.
根据题意,得W=40t+10(42-t)=30t+420.
因为30>0,所以W随t的增大而增大,
所以当t=14时,Wmin=30×14+420=840.
故购进A种树苗14棵,B种树苗28棵时,费用最少,最省费用是840元.
26. 解:(1) 4 500 1 500 30 150
(2) 根据题意,得小亮的实际速度为1 500÷15=100(m/min),
当0≤x≤15时,s=4 500-(150+100)x=-250x+4 500;
当15<x≤20时,s=4 500-(150+100)×15-150(x-15)=-150x+3 000;
当20<x≤30时,s=150(x-20)=150x-3 000;
当30<x≤60时,s=1 500+100(x-30)=100x-1 500.
综上所述,s与x的函数表达式为s=
图象如图所示:
(3) x的取值范围是10≤x≤35.
27. (1) 证明:①因为AB=AC,D是BC的中点,
所以∠BAF=∠CAF.
在△BAF和△CAF中,
所以△BAF≌△CAF(SAS),
所以∠ABF=∠ACF.
因为AB=AC,△ACE是等腰直角三角形,
所以AB=AE,所以∠ABE=∠AEB,
所以∠AEB=∠ACF.
②因为△BAF≌△CAF,所以BF=CF.
因为∠AGF=∠AEB+∠EAG,∠AGF=∠ACF+∠CFG,∠AEB=∠ACF,
所以∠CFG=∠EAG=90°,
所以EF2+BF2=EF2+CF2=EC2.
因为△ACE是等腰直角三角形,
所以∠CAE=90°,AC=AE,
所以EC2=AC2+AE2=2AC2,
即EF2+BF2=2AC2.
(2) 解:△BCF为等边三角形.理由如下:
因为AE=EF,所以∠FAE=∠AFE.
因为△ACE为等边三角形,
所以AE=CE,∠AEC=60°,所以EF=CE,
所以∠EFC=∠ECF,
所以∠AFC=∠AFE+∠CFE=(180°-∠AEF)+(180°-∠CEF)=(360°-∠AEF-∠CEF)=×(360°-60°)=150°.
由(1)可知,BF=CF,∠AFB=∠AFC,
所以∠BFC=360°-∠AFB-∠AFC=60°,
所以△BCF为等边三角形.
28. 解:(1) ①由题意,得
解得
②如图1,作点B关于x轴的对称点B′,连接AB′交x轴于点P,则PA+PB最小.
设直线AB′的函数表达式为y=kx+m,
所以
解得
所以y=x+,
当y=0时,0=x+,解得x=-,
所以点P的坐标为(-,0).
③如图1,作点B关于y轴的对称点B″(2,1),作直线AB″交y轴于点Q,
此时t=QA-QB-PA-PB最大.
设直线AB″的函数表达式为y=px+q,则
解得所以y=x-2,
当x=0时,y=-2,
所以点Q的坐标为(0,-2).
因为QA-QB=QA-QB″=AB″==,PA+PB=PA+PB′=AB′==,
所以tmax=QA-QB-PA-PB=-.
(2) 如图2,作PG⊥x轴,截取PG=OP.
因为PM=ON,∠GPM=∠PON=90°,
所以△GPM≌△PON(SAS),
所以PN=GM,
所以PN+MQ=GM+MQ≥GQ,当且仅当G,M,Q三点共线时,PM+QN最小.
因为点G(-,),Q(0,-2),
所以直线GQ的函数表达式为y=-x-2,
当y=0时,-x-2=0,解得x=-,
所以点M的坐标为(-,0).
图1 图2
(时间:120分钟 满分:150分)
一、 选择题(每小题3分,共24分)
1. (2025东台期末)在平面直角坐标系中,点P(4,-2)所在的象限为( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 如图,已知CD=CA,∠D=∠A,添加下列条件仍不能证明△DEC≌△ABC的是( )
A. ∠DEC=∠B B. ∠ACD=∠BCE C. CE=CB D. DE=AB
图1 图2
(第2题) (第7题) (第8题)
3. (2024扬州宝应期末)下列结论中,正确的是( )
A. 81的立方根是3 B. 的平方根是±4
C. 立方根等于平方根的数是1 D. 4的算术平方根是2
4. 下列各组数中,是勾股数的是( )
A. 12,15,18 B. 6,8,12 C. 4,5,6 D. 7,24,25
5. 关于直线l:y=kx+k(k≠0),下列说法中不正确的是( )
A. 点(0,k)在直线l上 B. 直线l经过定点(-1,0)
C. 当k>0时,y随x的增大而增大 D. 直线l经过第一、二、三象限
6. (2024常州溧阳期末)已知点A(,m),B(2,n)在一次函数y=ax+b(a>0)的图象上,则m与n的大小关系是( )
A. m>n B. m=n C. m<n D. 无法确定
7. (2024南京鼓楼期末)如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,点A在ED上.若AE=1,AD=3,则BC的长为( )
A. B. C. 2.5 D. 2
8. 如图1(图中各角均为直角),动点P从点A出发,以每秒1个单位长度的速度沿A→B→C→D→E路线匀速运动,△AFP的面积 y与点P运动的时间x(s)之间的函数关系图象如图2所示,则CD的长为( )
A. 5 B. 6 C. 7 D. 8
二、 填空题(每小题3分,共30分)
9. 36的平方根是 .
10. -π的绝对值是 .
11. 点A(3,5)关于x轴对称的点的坐标是 .
12. 已知点P(m-2,2m-1)在第二象限,则实数m的取值范围是 .
13. 已知a-1的平方根是±2,b+1的立方根为2,则代数式的值为 .
14. (2024南京鼓楼期末)如图,一架2.5 m长的梯子AB,斜靠在竖直的墙AC上,这时梯子的底部B到墙底端C的距离为1.5 m,则梯子的顶端距离地面为 m.
(第14题) (第15题) (第16题) (第17题) (第18题)
15. 如图,在平面直角坐标系中,点A的坐标为(-6,0),线段AB向右平移4个单位长度到线段CD,线段CD与y轴交于点E,若△CEO的面积为4,则点E的坐标为 .
16. 如图,直线l1:y=-x+m与x轴交于点A,直线l2:y=2x+n与y轴交于点B,与直线l1交于点P(2,2),则△PAB的面积为 .
17. 如图,在Rt△ABC中,∠C=90°,AB=5 cm,AC=3 cm,动点P从点B出发,沿射线BC以2 cm/s的速度移动,设运动的时间为t s,则当t= 时,△ABP为直角三角形.
18. (2024苏州姑苏期末)如图,△ABC的三个顶点坐标分别为A(-6,0),B(0,8),C(9,0),M是线段OB上的一点,连接AM并延长交BC于点N.若AM平分∠BAC,则点N的坐标是 .
三、 解答题(共96分)
19. (10分)(2025泰州姜堰期末)(1) 计算:()2+-;
(2) 已知(x+1)3+1=0,求x的值.
20. (8分)如图,在四边形ABCD中,AB=DC,延长CB到点E,使BE=AD,连接AE,AC,且AE=AC,求证:AD∥EC.
21. (8分)(2024南京秦淮期末)如图,在△ABC中,∠C=90°,AC=8,AB的垂直平分线MN交AC于点D,连接BD.
(1) 若∠A=25°,求∠DBC的度数;
(2) 若BC=4,求BD的长.
22. (8分)(2024南京鼓楼期末)如图,在△ABC中,AB=AC,△ADC和△ABE分别是以AC,AB为腰的等腰直角三角形,BE与CD相交于点F.
(1) 求证:∠FBC=∠FCB;
(2) 连接AF,求证:AF⊥BC.
23. (8分)如图,已知直线y=kx+b经过点A(5,0),B(1,4).
(1) 求直线AB的函数表达式;
(2) 若直线y=2x-4与直线AB相交于点C,求点C的坐标;
(3) 根据图象,写出关于x的不等式2x-4>kx+b的解集.
24. (10分)如图,在△ABC中,∠ACB,∠ABC的平分线l1,l2相交于点O.
(1) 求证:点O在∠BAC的平分线上;
(2) 连接OA,若AB=AC=5,OB=4,OA=2,求点O到边BC的距离.
25. (10分)某小区为了绿化环境,计划分两次购进A,B两种树苗,第一次购进A种树苗30棵,B种树苗15棵,共花费1 350元;第二次购进A种树苗24棵,B种树苗10棵,共花费1 060元(两次购进的A,B两种树苗各自的单价均不变).
(1) A,B两种树苗每棵的价格分别是多少元?
(2) 若购买A,B两种树苗共42棵,总费用为W元,购买A种树苗t棵,B种树苗的数量不超过A种树苗数量的2倍.求W与t的函数关系式.请设计出最省钱的购买方案,并求出此方案的总费用.
26. (10分)小明从A地匀速前往B地,同时小亮从B地匀速前往A地,图1表示两人距离B地的路程y(m)与行驶时间x(min)之间的函数关系.马小虎审题不清,将“两人距离B地的路程y”看成了“两人距离A地的路程y”,由此得到小明的速度为100 m/min.
(1) A地与B地的距离为 m,a= m,b= min,小明的实际速度为 m/min;
(2) 求当0≤x≤60时,两人的距离s(m)与x(min)的函数表达式,并在图2中画出图象;
(3) 当两人之间的距离不大于2 000 m时,直接写出x的取值范围.
图1 图2
27. (12分)在△ABC中,AB=AC,D是边BC的中点,连接AD.
(1) 如图1,若以AC为腰向外作等腰直角三角形ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.求证:
①∠AEB=∠ACF;
②EF2+BF2=2AC2;
(2) 如图2,若以AC为边向外作等边三角形ACE,在AD上取一点F,使得AE=EF,请判断△BCF的形状,并说明理由.
图1 图2
28. (12分)(2025泰州兴化期末)
【问题导入】
如图1,在直线l上找一点P,如何使得PA+PB最小?
图1 图2
小华同学的思路:作点A关于直线l的对称点A′,连接BA′,与直线l交于点P.由对称可得PA′=PA,所以PA+PB=PA′+PB≥A′B,当且仅当A′,P,B三点共线时,PA′+PB=A′B,此时PA+PB最小.
如图2,在直线l上找一点P,如何使得|PA-PB|最大?
小明同学的思路:作点A关于直线l的对称点A′,连接BA′并延长交直线l于点P.由对称可得PA′=PA,所以|PA-PB|=|PA′-PB|≤A′B,当且仅当A′,P,B三点共线时,|PA-PB|=A′B,此时|PA-PB|最大.
可见,解此类问题的关键是将问题转化为“两点之间线段最短”来解决.
【理解运用】
(1) 如图3,直线y=x+b上有点A(4,a),B(-2,1),点P在x轴上运动,点Q在直线AB下方的y轴上运动.
①求a,b的值;
②当PA+PB最小时,求点P的坐标;
③令t=QA-QB-PA-PB,当t的值最大时,求点Q的坐标及t的最大值;
【深度探究】
(2) 在(1)的条件下,且满足t=QA-QB-PA-PB,当t的值最大时,若M,N分别是线段OP,OQ上的动点,且PM=ON,连接PN,MQ,当PN+MQ最小时,求点M的坐标.
图3 备用图
期末综合测试卷A
1. D 2. C 3. D 4. D 5. D 6. C 7. A 8. B
9. ±6 10. π- 11. (3,-5) 12. <m<2 13.
14. 2 15. (0,4) 16. 10 17. 2或 18. (,)
19. 解:(1) ()2+-
=3+(-4)-2
=-1+(-2)
=-3.
(2) (x+1)3+1=0,
(x+1)3=-1,
x+1=-1,
x=-2.
20. 证明:在△ABE和△CDA中,
所以△ABE≌△CDA(SSS),所以∠E=∠CAD.
因为AE=AC,所以∠E=∠ACE,
所以∠ACE=∠CAD,所以AD∥EC.
21. 解:(1) 因为MN垂直平分AB,
所以DA=DB,所以∠DBA=∠A=25°.
因为∠C=90°,
所以∠ABC=90°-25°=65°,
所以∠DBC=∠ABC-∠DBA=65°-25°=40°.
(2) 设BD=x,则DA=x,所以CD=8-x,
在△BCD中,由勾股定理,得BD2=CD2+BC2,
所以x2=(8-x)2+42,解得x=5,
所以BD=5.
22. 证明:(1) 因为AB=AC,△ADC和△ABE分别是以AC,AB为腰的等腰直角三角形,
所以AD=AE=AB=AC,∠DAC=∠EAB=90°,BE=CD,
所以∠DAB=90°-∠DAE=∠EAC,
所以△ABD≌△ACE(SAS),
所以BD=CE.
因为CD=BE,BC=BC,
所以△BCD≌△CBE(SSS),
所以∠BCD=∠CBE,
即∠FBC=∠FCB.
(2) 由(1)知,BF=FC.
因为AB=AC,
所以AF是BC的垂直平分线,
所以AF⊥BC.
23. 解:(1) 因为直线y=kx+b经过点A(5,0),B(1,4),
所以解得
所以直线AB的函数表达式为y=-x+5.
(2) 若直线y=2x-4与直线AB相交于点C,
则解得
所以点C的坐标为(3,2).
(3) 根据图象可得x>3.
24. (1) 证明:过点O作OD⊥AB,OE⊥AC,OF⊥BC,垂足分别为D,E,F.
因为∠ACB,∠ABC的平分线l1,l2相交于点O,
所以OD=OF,OE=OF,
所以OD=OE,
所以点O在∠BAC的平分线上.
(2) 解:因为AB=AC,AO平分∠BAC,
所以AO⊥BC.
因为OF⊥BC,所以A,O,F三点共线.
设OF=x,则AF=OA+OF=x+2.
在Rt△ABF中,BF2=AB2-AF2,
即BF2=25-(x+2)2,
在Rt△OBF中,BF2=OB2-OF2,
即BF2=16-x2,
所以25-(x+2)2=16-x2,
解得x=,所以OF=,
所以点O到边BC的距离是.
25. 解:(1) 设A种树苗每棵的价格是x元,B种树苗每棵的价格是y元.
根据题意,得解得
所以A种树苗每棵的价格是40元,B种树苗每棵的价格是10元.
(2) 由购买A种树苗的数量为t棵,得购买B种树苗的数量为(42-t)棵.
因为B种树苗的数量不超过A种树苗数量的2倍,
所以42-t≤2t,解得t≥14.
根据题意,得W=40t+10(42-t)=30t+420.
因为30>0,所以W随t的增大而增大,
所以当t=14时,Wmin=30×14+420=840.
故购进A种树苗14棵,B种树苗28棵时,费用最少,最省费用是840元.
26. 解:(1) 4 500 1 500 30 150
(2) 根据题意,得小亮的实际速度为1 500÷15=100(m/min),
当0≤x≤15时,s=4 500-(150+100)x=-250x+4 500;
当15<x≤20时,s=4 500-(150+100)×15-150(x-15)=-150x+3 000;
当20<x≤30时,s=150(x-20)=150x-3 000;
当30<x≤60时,s=1 500+100(x-30)=100x-1 500.
综上所述,s与x的函数表达式为s=
图象如图所示:
(3) x的取值范围是10≤x≤35.
27. (1) 证明:①因为AB=AC,D是BC的中点,
所以∠BAF=∠CAF.
在△BAF和△CAF中,
所以△BAF≌△CAF(SAS),
所以∠ABF=∠ACF.
因为AB=AC,△ACE是等腰直角三角形,
所以AB=AE,所以∠ABE=∠AEB,
所以∠AEB=∠ACF.
②因为△BAF≌△CAF,所以BF=CF.
因为∠AGF=∠AEB+∠EAG,∠AGF=∠ACF+∠CFG,∠AEB=∠ACF,
所以∠CFG=∠EAG=90°,
所以EF2+BF2=EF2+CF2=EC2.
因为△ACE是等腰直角三角形,
所以∠CAE=90°,AC=AE,
所以EC2=AC2+AE2=2AC2,
即EF2+BF2=2AC2.
(2) 解:△BCF为等边三角形.理由如下:
因为AE=EF,所以∠FAE=∠AFE.
因为△ACE为等边三角形,
所以AE=CE,∠AEC=60°,所以EF=CE,
所以∠EFC=∠ECF,
所以∠AFC=∠AFE+∠CFE=(180°-∠AEF)+(180°-∠CEF)=(360°-∠AEF-∠CEF)=×(360°-60°)=150°.
由(1)可知,BF=CF,∠AFB=∠AFC,
所以∠BFC=360°-∠AFB-∠AFC=60°,
所以△BCF为等边三角形.
28. 解:(1) ①由题意,得
解得
②如图1,作点B关于x轴的对称点B′,连接AB′交x轴于点P,则PA+PB最小.
设直线AB′的函数表达式为y=kx+m,
所以
解得
所以y=x+,
当y=0时,0=x+,解得x=-,
所以点P的坐标为(-,0).
③如图1,作点B关于y轴的对称点B″(2,1),作直线AB″交y轴于点Q,
此时t=QA-QB-PA-PB最大.
设直线AB″的函数表达式为y=px+q,则
解得所以y=x-2,
当x=0时,y=-2,
所以点Q的坐标为(0,-2).
因为QA-QB=QA-QB″=AB″==,PA+PB=PA+PB′=AB′==,
所以tmax=QA-QB-PA-PB=-.
(2) 如图2,作PG⊥x轴,截取PG=OP.
因为PM=ON,∠GPM=∠PON=90°,
所以△GPM≌△PON(SAS),
所以PN=GM,
所以PN+MQ=GM+MQ≥GQ,当且仅当G,M,Q三点共线时,PM+QN最小.
因为点G(-,),Q(0,-2),
所以直线GQ的函数表达式为y=-x-2,
当y=0时,-x-2=0,解得x=-,
所以点M的坐标为(-,0).
图1 图2
同课章节目录
