期末综合测试卷B 同步练(含答案) 2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 期末综合测试卷B 同步练(含答案) 2025-2026学年数学苏科版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 287.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 15:40:56 | ||
图片预览




文档简介
期末综合测试卷B
(时间:120分钟 满分:150分)
一、 选择题(每小题3分,共24分)
1. 若一个等腰三角形的两边长分别为2 cm,4 cm,则它的周长是 ( )
A. 8 cm B. 8 cm或10 cm
C. 10 cm D. 6 cm或8 cm
2. (2024南京玄武期末)如图,用直尺和圆规作∠AOB的平分线OC,则△DOC≌△EOC的依据是( )
A. SSS B. SAS C. ASA D. AAS
(第2题) (第5题) (第6题) (第8题)
3. (2024南京玄武期末)若m<A. 1 B. 2 C. 3 D. 4
4. (2025泰州姜堰期末)下列各组数中,是“勾股数”的一组是( )
A. 4,5,6 B. 1.5,2,2.5 C. 6,8,10 D. 1,,2
5. (2024南京玄武期末)如图,在△ABC中,∠C=90°,D是边BC上的点.若BD=3,DC=2,则AB2-AD2的值为( )
A. 13 B. 21 C. 25 D. 29
6. 如图,在等边三角形ABC中,D,E分别是边AB,AC上的点,且AD=CE,则∠ADC+∠BEA的结果为( )
A. 180° B. 170° C. 160° D. 150°
7. 在平面直角坐标系xOy中,已知A(-1,0),B(3,0),C(0,-1)三点,D(1,m)是一个动点,则当△ACD的周长最小时,△ABD的面积为( )
A. B. C. D.
8. 如图,P为△ABC三边垂直平分线的交点,∠PAC=22°,∠PCB=33°,则∠PAB的度数为( )
A. 33° B. 35° C. 37° D. 39°
二、 填空题(每题3分,共30分)
9. 无理数的整数部分是 .
10. (2024苏州姑苏期末)已知A(x1,y1),B(x2,y2)是函数y=-x+2图象上的两个点,若x1-x2<0,则y1 y2.(填“>”“<”或“=”)
11. 七大洲的总面积约为1.49亿平方千米,这个数据1.49亿精确到 位.
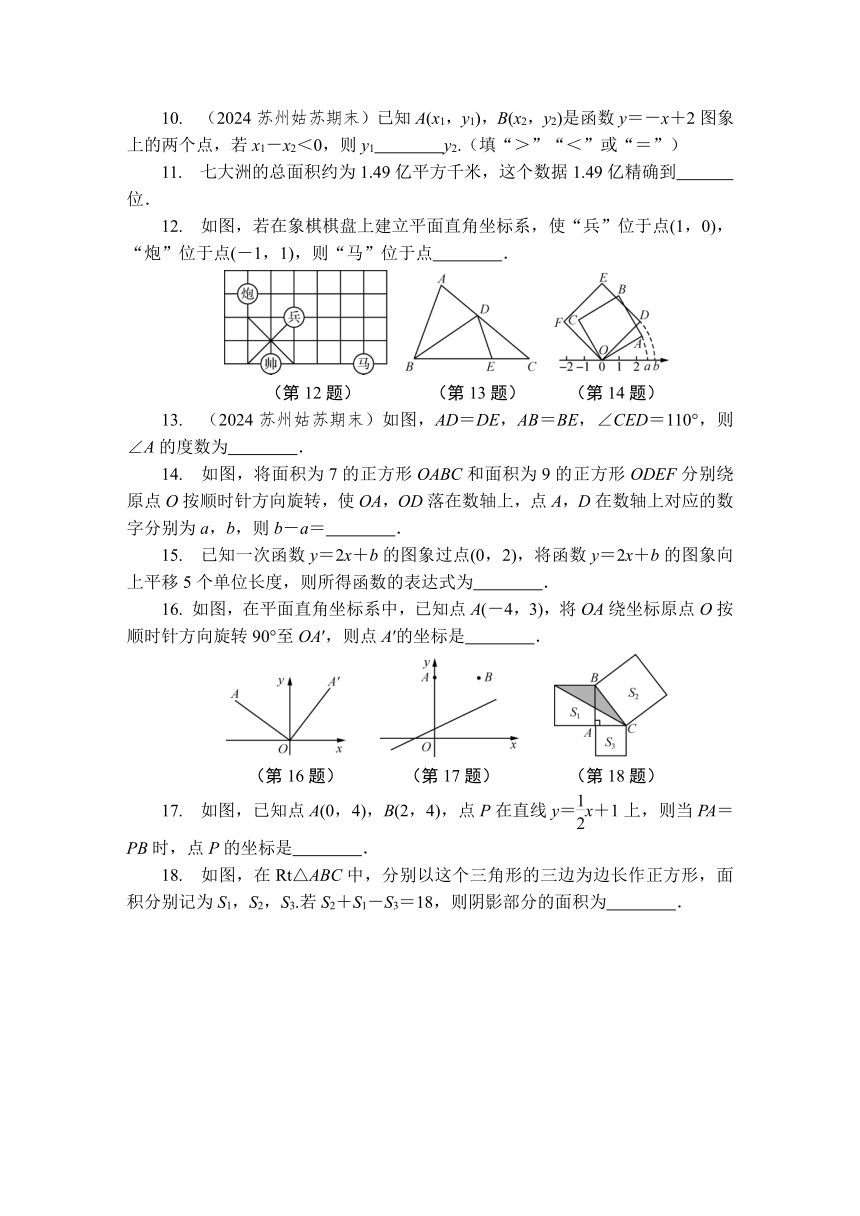
12. 如图,若在象棋棋盘上建立平面直角坐标系,使“兵”位于点(1,0),“炮”位于点(-1,1),则“马”位于点 .
(第12题) (第13题) (第14题)
13. (2024苏州姑苏期末)如图,AD=DE,AB=BE,∠CED=110°,则∠A的度数为 .
14. 如图,将面积为7的正方形OABC和面积为9的正方形ODEF分别绕原点O按顺时针方向旋转,使OA,OD落在数轴上,点A,D在数轴上对应的数字分别为a,b,则b-a= .
15. 已知一次函数y=2x+b的图象过点(0,2),将函数y=2x+b的图象向上平移5个单位长度,则所得函数的表达式为 .
16. 如图,在平面直角坐标系中,已知点A(-4,3),将OA绕坐标原点O按顺时针方向旋转90°至OA′,则点A′的坐标是 .
(第16题) (第17题) (第18题)
17. 如图,已知点A(0,4),B(2,4),点P在直线y=x+1上,则当PA=PB时,点P的坐标是 .
18. 如图,在Rt△ABC中,分别以这个三角形的三边为边长作正方形,面积分别记为S1,S2,S3.若S2+S1-S3=18,则阴影部分的面积为 .
三、 解答题(共96分)
19. (10分)(2025连云港海州期末)
(1) 计算:(4-π)0-+;
(2) 解方程:49x2-16=0.
20. (8分)(2024盐城建湖期末)如图,在Rt△ABC中,∠C=90°.
(1) 在边BC上作一点P,使点P到边AB,AC的距离相等(要求:尺规作图,不写作法,保留作图痕迹);
(2) 在(1)的条件下,若AC=5,AB=13,求CP的长.
21. (8分)如图,正比例函数y=-3x的图象与一次函数y=kx+b的图象交于点P(m,3),一次函数的图象经过点B(1,1),与y轴的交点为D,与x轴的交点为C.求:
(1) 一次函数的表达式;
(2) △COP的面积.
22. (8分)(2024南京玄武期末)如图,在△ABC中,AB=AC,延长BC到点D,使BC=CD,连接AD,过点C作CE⊥BD,与AD交于点E.
(1) 求证:∠CAD=∠ABE;
(2) 探索线段AE,BE之间的数量关系,并说明理由.
23. (8分)(2025扬州仪征期末)观察下面图形,已知每个小正方形的边长为1.
(1) 图1中阴影正方形的面积是 ,边长是 ;
(2) 请用无刻度的直尺和圆规在图2的数轴上作出点M,使得点M表示的数为(保留作图痕迹,不写作法).
图1 图2
24. (10分)(2024盐城建湖期末)“互联网+”让我国经济更具活力.牡丹花会期间,某网店直接从工厂购进A,B两款花会纪念钥匙扣进行销售,进货价和销售价如下表所示.
A款钥匙扣 B款钥匙扣
进货价/(元/件) 20 25
销售价/(元/件) 30 37
(1) 网店第一次用1 100元购进A,B两款钥匙扣共50件,求两款钥匙扣分别购进的件数;
(2) 第一次购进的花会纪念钥匙扣售完后,该网店计划再次购进A,B两款钥匙扣共240件(进货价和销售价都不变),且第二次进货总价不高于5 800元.网店这次应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少?
25. (10分)甲、乙两人在一条长400 m的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3 s,在跑步过程中甲、乙两人之间的距离y(m)与乙出发的时间x(s)之间的函数关系如图所示.求:
(1) 乙的速度;
(2) 离开起点后,当甲、乙两人第一次相遇时,距离起点多远?
(3) 当乙到达终点时,甲距离终点还有多远?
26. (10分)如图1,在等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E.
(1) 求证:△BEC≌△CDA;
(2) 已知直线l1:y=-x-4与y轴交于点A. 将直线l1绕点A按逆时针方向旋转45°至直线l2,如图2,求直线l2的函数表达式.
图1 图2
27. (12分)(2024启东期末)如图1,在△ABC中,∠ACB=90°,AC=BC,BD为边AC上的中线,过点A作AE⊥BD,交BD的延长线于点E.
(1) ∠EAD+∠ABD的度数为 ;
(2) 如图2,过点C作CF⊥BD于点F,求证:BF=2AE;
(3) 在(2)的条件下,如图3,在△ABC的外部作∠BCG=∠BCF,且满足CG=CF,连接AG.若AB=4,求AG的长.
图1 图2 图3
28. (12分)(2025扬州江都期末)
【定义一】对于给定的两个函数,任取自变量x的一个值,当x≥0时,它们对应的函数值相等;当x<0时,它们对应的函数值互为相反数.我们称这样的两个函数互为“友好函数”.
例如:一次函数y=x-1,它的“友好函数”为y=
【定义二】在平面直角坐标系中,将经过点(0,b)且垂直于y轴的直线记为直线y=b.
已知一次函数y=2x-4,请回答下列问题:
(1) 该一次函数的“友好函数”为 ;
(2) 已知点A(a,2)在该一次函数的“友好函数”的图象上,求a的值;
(3) 当-1≤x≤1时,求该一次函数的“友好函数”的最大值和最小值;
(4) 已知直线y=b与该一次函数的“友好函数”的图象只有一个交点,直接写出b的取值范围.
期末综合测试卷B
1. C 2. A 3. C 4. C 5. B 6. A 7. C 8. B 9. 2
10. > 11. 百万 12. (4,-2) 13. 70° 14. 3-
15. y=2x+7 16. (3,4) 17. (1,) 18.
19. 解:(1) (4-π)0-+
=1-6+3
=-2.
(2) 因为49x2-16=0,
所以49x2=16,即x2=,
解得x=或x=-.
20. 解:(1) 如图,P就是所求的点.
(2) 作PD⊥AB于点D,由尺规作图可知,AP是∠BAC的平分线.
因为∠C=∠PDA=90°,所以CP=DP,
所以BC===12.
在Rt△ACP和Rt△ADP中,
所以△ACP≌△ADP(HL),
所以AD=AC=5.
设CP=x,
则BP=BC-CP=12-x,BD=AB-AD=8.
在Rt△BDP中,由勾股定理,得BP2=BD2+DP2,
即(12-x)2=x2+82,解得x=,
所以CP=.
21. 解:(1) 因为正比例函数y=-3x的图象过点P(m,3),
所以3=-3m,解得m=-1,
所以点P的坐标为(-1,3).
因为一次函数y=kx+b的图象过点P(-1,3),B(1,1),
所以解得
所以一次函数的表达式为y=-x+2.
(2) 由(1)知,一次函数表达式为y=-x+2,
令y=0,即-x+2=0,解得x=2,
所以点C的坐标为(2,0),
所以OC=2,
所以S△COP=×2×3=3.
22. (1) 证明:因为AB=AC,所以∠ABC=∠ACB.
因为CE⊥BD,BC=CD,
所以BE=DE,所以∠EBD=∠EDB.
因为∠ABC=∠ABE+∠EBD,∠ACB=∠EDB+∠CAD,
所以∠CAD=∠ABE.
(2) 解:BE=2AE.理由如下:
在AD上截取AH=BE,连接CH.
在△ABE和△CAH中,
所以△ABE≌△CAH(SAS),
所以EA=HC.
因为AH=BE=DE,所以AE=DH,
所以CH=DH,
所以∠HCD=∠HDC.
因为CE⊥BD,所以∠ECH=∠CEH,
所以CH=HE,所以DE=2CH,
所以BE=2AE.
23. 解:(1) 13
(2) 如图即为所求.
24. 解:(1) 设购进A款钥匙扣x件,B款钥匙扣y件.
由题意,得解得
故购进A款钥匙扣30件,B款钥匙扣20件.
(2) 设购进m件A款钥匙扣,则购进(240-m)件B款钥匙扣.
由题意,得20m+25(240-m)≤5 800,
解得m≥40.
设再次购进的A,B两款钥匙扣全部售出后获得的总利润为w元,则w=(30-20)m+(37-25)(240-m)=-2m+2 880.
因为-2<0,
所以w随m的增大而减小,
所以当m=40时,w取得最大值,最大值为-2×40+2 880=2 800(元),
此时240-40=200(件).
故当购进40件A款钥匙扣,200件B款钥匙扣时,才能获得最大销售利润,最大销售利润是2 800元.
25. 解:(1) 乙的速度为400÷80=5(m/s).
(2) 易得甲的速度为=4(m/s).
设甲、乙两人第一次相遇时,乙用了x s,
则5x=4(x+3),解得x=12,
所以5x=60,
所以当甲、乙两人第一次相遇时,距离起点60 m.
(3) 400-4×(80+3)=68(m),
所以当乙到达终点时,甲距离终点还有68 m.
26. (1) 证明:如图1,因为AD⊥ED,BE⊥ED,
所以∠E=∠D=90°,所以∠3+∠1=90°.
又∠ACB=90°,所以∠2+∠3=90°,所以∠1=∠2.
在△BEC和△CDA中,
所以△BEC≌△CDA(AAS).
(2) 解:如图2,过点B作BM⊥AB,交直线l2于点M,过点M作MN⊥x轴于点N.
由题意知,∠BAM=45°,
所以△ABM为等腰直角三角形.
由(1)可知,△ABO≌△BMN,所以MN=BO,NB=OA.
因为直线l1:y=-x-4,
所以点A,B的坐标分别为(0,-4),(-3,0),
所以MN=BO=3,BN=OA=4,则ON=7,
所以点M(-7,-3).
设直线l2的函数表达式为y=kx+b,
则解得
所以直线l2的函数表达式为y=-x-4.
图1 图2
27. (1) 45°
(2) 证明:在BF上取一点P,使得BP=AE,连接CP,CE.
由题意可得∠EAD=∠CBD.
因为AE=BP,AC=BC,
所以△AEC≌△BPC(SAS),
所以CE=CP,∠ACE=∠BCP,
所以∠ACE+∠DCP=∠BCP+∠DCP=∠ACB=90°,即∠ECP=90°,
所以△CPE是等腰直角三角形,
所以∠CEP=∠CPE=45°.
因为CF⊥BD,
所以∠CFD=90°,∠PCF=∠ECP=45°,EF=PF,
所以CF=PE=PF.
因为BD为边AC上的中线,所以AD=CD.
因为∠AED=∠CFD=90°,∠ADE=∠CDF,
所以△ADE≌△CDF(AAS),
所以AE=CF,所以AE=PF,
所以BF=BP+PF=2AE.
(3) 解:连接BG,取BG的中点H,连接CE,CH,AH,如图所示,
则BH=BG.
因为CG=CF,∠BCG=∠BCF,BC=BC,
所以△BCF≌△BCG(SAS),
所以∠FBC=∠GBC,BF=BG,
所以BH=BF.
由(2),得BF=2AE,
所以BH=AE.
因为∠GBC=∠FBC=∠EAC,
所以∠EAC+∠CAB=∠GBC+∠ABC,
即∠EAB=∠HBA.
又因为AB=BA,
所以△ABE≌△BAH(SAS),
所以∠BHA=∠AEB=90°,
所以AH⊥BG.
因为BH=GH,
所以AG=AB=4.
28. 解:(1) y=
(2) 当a≥0时,因为点A(a,2)在该一次函数的“友好函数”的图象上,
所以2a-4=2,
解得a=3,符合题意;
当a<0时,因为点A(a,2)在该一次函数的“友好函数”的图象上,
所以-2a+4=2,
解得a=1>0,不符合题意.
综上,a的值为3.
(3) 当-1≤x<0时,y=-2x+4,y随x的增大而减小,
当0≤x≤1时,y=2x-4,y随x的增大而增大,
且当x=-1时,y=6;当x=0时,y=-4;
当x=1时,y=-2,
所以当x=-1时,y有最大值6;
当x=0时,y有最小值-4.
综上,该一次函数的“友好函数”的最大值为6,最小值为-4.
(4) 由题意,画出一次函数y=2x-4的“友好函数”y=的图象如图所示.
因为直线y=b与该一次函数的“友好函数”的图象只有一个交点,
所以-4≤b≤4.
(时间:120分钟 满分:150分)
一、 选择题(每小题3分,共24分)
1. 若一个等腰三角形的两边长分别为2 cm,4 cm,则它的周长是 ( )
A. 8 cm B. 8 cm或10 cm
C. 10 cm D. 6 cm或8 cm
2. (2024南京玄武期末)如图,用直尺和圆规作∠AOB的平分线OC,则△DOC≌△EOC的依据是( )
A. SSS B. SAS C. ASA D. AAS
(第2题) (第5题) (第6题) (第8题)
3. (2024南京玄武期末)若m<
4. (2025泰州姜堰期末)下列各组数中,是“勾股数”的一组是( )
A. 4,5,6 B. 1.5,2,2.5 C. 6,8,10 D. 1,,2
5. (2024南京玄武期末)如图,在△ABC中,∠C=90°,D是边BC上的点.若BD=3,DC=2,则AB2-AD2的值为( )
A. 13 B. 21 C. 25 D. 29
6. 如图,在等边三角形ABC中,D,E分别是边AB,AC上的点,且AD=CE,则∠ADC+∠BEA的结果为( )
A. 180° B. 170° C. 160° D. 150°
7. 在平面直角坐标系xOy中,已知A(-1,0),B(3,0),C(0,-1)三点,D(1,m)是一个动点,则当△ACD的周长最小时,△ABD的面积为( )
A. B. C. D.
8. 如图,P为△ABC三边垂直平分线的交点,∠PAC=22°,∠PCB=33°,则∠PAB的度数为( )
A. 33° B. 35° C. 37° D. 39°
二、 填空题(每题3分,共30分)
9. 无理数的整数部分是 .
10. (2024苏州姑苏期末)已知A(x1,y1),B(x2,y2)是函数y=-x+2图象上的两个点,若x1-x2<0,则y1 y2.(填“>”“<”或“=”)
11. 七大洲的总面积约为1.49亿平方千米,这个数据1.49亿精确到 位.
12. 如图,若在象棋棋盘上建立平面直角坐标系,使“兵”位于点(1,0),“炮”位于点(-1,1),则“马”位于点 .
(第12题) (第13题) (第14题)
13. (2024苏州姑苏期末)如图,AD=DE,AB=BE,∠CED=110°,则∠A的度数为 .
14. 如图,将面积为7的正方形OABC和面积为9的正方形ODEF分别绕原点O按顺时针方向旋转,使OA,OD落在数轴上,点A,D在数轴上对应的数字分别为a,b,则b-a= .
15. 已知一次函数y=2x+b的图象过点(0,2),将函数y=2x+b的图象向上平移5个单位长度,则所得函数的表达式为 .
16. 如图,在平面直角坐标系中,已知点A(-4,3),将OA绕坐标原点O按顺时针方向旋转90°至OA′,则点A′的坐标是 .
(第16题) (第17题) (第18题)
17. 如图,已知点A(0,4),B(2,4),点P在直线y=x+1上,则当PA=PB时,点P的坐标是 .
18. 如图,在Rt△ABC中,分别以这个三角形的三边为边长作正方形,面积分别记为S1,S2,S3.若S2+S1-S3=18,则阴影部分的面积为 .
三、 解答题(共96分)
19. (10分)(2025连云港海州期末)
(1) 计算:(4-π)0-+;
(2) 解方程:49x2-16=0.
20. (8分)(2024盐城建湖期末)如图,在Rt△ABC中,∠C=90°.
(1) 在边BC上作一点P,使点P到边AB,AC的距离相等(要求:尺规作图,不写作法,保留作图痕迹);
(2) 在(1)的条件下,若AC=5,AB=13,求CP的长.
21. (8分)如图,正比例函数y=-3x的图象与一次函数y=kx+b的图象交于点P(m,3),一次函数的图象经过点B(1,1),与y轴的交点为D,与x轴的交点为C.求:
(1) 一次函数的表达式;
(2) △COP的面积.
22. (8分)(2024南京玄武期末)如图,在△ABC中,AB=AC,延长BC到点D,使BC=CD,连接AD,过点C作CE⊥BD,与AD交于点E.
(1) 求证:∠CAD=∠ABE;
(2) 探索线段AE,BE之间的数量关系,并说明理由.
23. (8分)(2025扬州仪征期末)观察下面图形,已知每个小正方形的边长为1.
(1) 图1中阴影正方形的面积是 ,边长是 ;
(2) 请用无刻度的直尺和圆规在图2的数轴上作出点M,使得点M表示的数为(保留作图痕迹,不写作法).
图1 图2
24. (10分)(2024盐城建湖期末)“互联网+”让我国经济更具活力.牡丹花会期间,某网店直接从工厂购进A,B两款花会纪念钥匙扣进行销售,进货价和销售价如下表所示.
A款钥匙扣 B款钥匙扣
进货价/(元/件) 20 25
销售价/(元/件) 30 37
(1) 网店第一次用1 100元购进A,B两款钥匙扣共50件,求两款钥匙扣分别购进的件数;
(2) 第一次购进的花会纪念钥匙扣售完后,该网店计划再次购进A,B两款钥匙扣共240件(进货价和销售价都不变),且第二次进货总价不高于5 800元.网店这次应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少?
25. (10分)甲、乙两人在一条长400 m的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3 s,在跑步过程中甲、乙两人之间的距离y(m)与乙出发的时间x(s)之间的函数关系如图所示.求:
(1) 乙的速度;
(2) 离开起点后,当甲、乙两人第一次相遇时,距离起点多远?
(3) 当乙到达终点时,甲距离终点还有多远?
26. (10分)如图1,在等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E.
(1) 求证:△BEC≌△CDA;
(2) 已知直线l1:y=-x-4与y轴交于点A. 将直线l1绕点A按逆时针方向旋转45°至直线l2,如图2,求直线l2的函数表达式.
图1 图2
27. (12分)(2024启东期末)如图1,在△ABC中,∠ACB=90°,AC=BC,BD为边AC上的中线,过点A作AE⊥BD,交BD的延长线于点E.
(1) ∠EAD+∠ABD的度数为 ;
(2) 如图2,过点C作CF⊥BD于点F,求证:BF=2AE;
(3) 在(2)的条件下,如图3,在△ABC的外部作∠BCG=∠BCF,且满足CG=CF,连接AG.若AB=4,求AG的长.
图1 图2 图3
28. (12分)(2025扬州江都期末)
【定义一】对于给定的两个函数,任取自变量x的一个值,当x≥0时,它们对应的函数值相等;当x<0时,它们对应的函数值互为相反数.我们称这样的两个函数互为“友好函数”.
例如:一次函数y=x-1,它的“友好函数”为y=
【定义二】在平面直角坐标系中,将经过点(0,b)且垂直于y轴的直线记为直线y=b.
已知一次函数y=2x-4,请回答下列问题:
(1) 该一次函数的“友好函数”为 ;
(2) 已知点A(a,2)在该一次函数的“友好函数”的图象上,求a的值;
(3) 当-1≤x≤1时,求该一次函数的“友好函数”的最大值和最小值;
(4) 已知直线y=b与该一次函数的“友好函数”的图象只有一个交点,直接写出b的取值范围.
期末综合测试卷B
1. C 2. A 3. C 4. C 5. B 6. A 7. C 8. B 9. 2
10. > 11. 百万 12. (4,-2) 13. 70° 14. 3-
15. y=2x+7 16. (3,4) 17. (1,) 18.
19. 解:(1) (4-π)0-+
=1-6+3
=-2.
(2) 因为49x2-16=0,
所以49x2=16,即x2=,
解得x=或x=-.
20. 解:(1) 如图,P就是所求的点.
(2) 作PD⊥AB于点D,由尺规作图可知,AP是∠BAC的平分线.
因为∠C=∠PDA=90°,所以CP=DP,
所以BC===12.
在Rt△ACP和Rt△ADP中,
所以△ACP≌△ADP(HL),
所以AD=AC=5.
设CP=x,
则BP=BC-CP=12-x,BD=AB-AD=8.
在Rt△BDP中,由勾股定理,得BP2=BD2+DP2,
即(12-x)2=x2+82,解得x=,
所以CP=.
21. 解:(1) 因为正比例函数y=-3x的图象过点P(m,3),
所以3=-3m,解得m=-1,
所以点P的坐标为(-1,3).
因为一次函数y=kx+b的图象过点P(-1,3),B(1,1),
所以解得
所以一次函数的表达式为y=-x+2.
(2) 由(1)知,一次函数表达式为y=-x+2,
令y=0,即-x+2=0,解得x=2,
所以点C的坐标为(2,0),
所以OC=2,
所以S△COP=×2×3=3.
22. (1) 证明:因为AB=AC,所以∠ABC=∠ACB.
因为CE⊥BD,BC=CD,
所以BE=DE,所以∠EBD=∠EDB.
因为∠ABC=∠ABE+∠EBD,∠ACB=∠EDB+∠CAD,
所以∠CAD=∠ABE.
(2) 解:BE=2AE.理由如下:
在AD上截取AH=BE,连接CH.
在△ABE和△CAH中,
所以△ABE≌△CAH(SAS),
所以EA=HC.
因为AH=BE=DE,所以AE=DH,
所以CH=DH,
所以∠HCD=∠HDC.
因为CE⊥BD,所以∠ECH=∠CEH,
所以CH=HE,所以DE=2CH,
所以BE=2AE.
23. 解:(1) 13
(2) 如图即为所求.
24. 解:(1) 设购进A款钥匙扣x件,B款钥匙扣y件.
由题意,得解得
故购进A款钥匙扣30件,B款钥匙扣20件.
(2) 设购进m件A款钥匙扣,则购进(240-m)件B款钥匙扣.
由题意,得20m+25(240-m)≤5 800,
解得m≥40.
设再次购进的A,B两款钥匙扣全部售出后获得的总利润为w元,则w=(30-20)m+(37-25)(240-m)=-2m+2 880.
因为-2<0,
所以w随m的增大而减小,
所以当m=40时,w取得最大值,最大值为-2×40+2 880=2 800(元),
此时240-40=200(件).
故当购进40件A款钥匙扣,200件B款钥匙扣时,才能获得最大销售利润,最大销售利润是2 800元.
25. 解:(1) 乙的速度为400÷80=5(m/s).
(2) 易得甲的速度为=4(m/s).
设甲、乙两人第一次相遇时,乙用了x s,
则5x=4(x+3),解得x=12,
所以5x=60,
所以当甲、乙两人第一次相遇时,距离起点60 m.
(3) 400-4×(80+3)=68(m),
所以当乙到达终点时,甲距离终点还有68 m.
26. (1) 证明:如图1,因为AD⊥ED,BE⊥ED,
所以∠E=∠D=90°,所以∠3+∠1=90°.
又∠ACB=90°,所以∠2+∠3=90°,所以∠1=∠2.
在△BEC和△CDA中,
所以△BEC≌△CDA(AAS).
(2) 解:如图2,过点B作BM⊥AB,交直线l2于点M,过点M作MN⊥x轴于点N.
由题意知,∠BAM=45°,
所以△ABM为等腰直角三角形.
由(1)可知,△ABO≌△BMN,所以MN=BO,NB=OA.
因为直线l1:y=-x-4,
所以点A,B的坐标分别为(0,-4),(-3,0),
所以MN=BO=3,BN=OA=4,则ON=7,
所以点M(-7,-3).
设直线l2的函数表达式为y=kx+b,
则解得
所以直线l2的函数表达式为y=-x-4.
图1 图2
27. (1) 45°
(2) 证明:在BF上取一点P,使得BP=AE,连接CP,CE.
由题意可得∠EAD=∠CBD.
因为AE=BP,AC=BC,
所以△AEC≌△BPC(SAS),
所以CE=CP,∠ACE=∠BCP,
所以∠ACE+∠DCP=∠BCP+∠DCP=∠ACB=90°,即∠ECP=90°,
所以△CPE是等腰直角三角形,
所以∠CEP=∠CPE=45°.
因为CF⊥BD,
所以∠CFD=90°,∠PCF=∠ECP=45°,EF=PF,
所以CF=PE=PF.
因为BD为边AC上的中线,所以AD=CD.
因为∠AED=∠CFD=90°,∠ADE=∠CDF,
所以△ADE≌△CDF(AAS),
所以AE=CF,所以AE=PF,
所以BF=BP+PF=2AE.
(3) 解:连接BG,取BG的中点H,连接CE,CH,AH,如图所示,
则BH=BG.
因为CG=CF,∠BCG=∠BCF,BC=BC,
所以△BCF≌△BCG(SAS),
所以∠FBC=∠GBC,BF=BG,
所以BH=BF.
由(2),得BF=2AE,
所以BH=AE.
因为∠GBC=∠FBC=∠EAC,
所以∠EAC+∠CAB=∠GBC+∠ABC,
即∠EAB=∠HBA.
又因为AB=BA,
所以△ABE≌△BAH(SAS),
所以∠BHA=∠AEB=90°,
所以AH⊥BG.
因为BH=GH,
所以AG=AB=4.
28. 解:(1) y=
(2) 当a≥0时,因为点A(a,2)在该一次函数的“友好函数”的图象上,
所以2a-4=2,
解得a=3,符合题意;
当a<0时,因为点A(a,2)在该一次函数的“友好函数”的图象上,
所以-2a+4=2,
解得a=1>0,不符合题意.
综上,a的值为3.
(3) 当-1≤x<0时,y=-2x+4,y随x的增大而减小,
当0≤x≤1时,y=2x-4,y随x的增大而增大,
且当x=-1时,y=6;当x=0时,y=-4;
当x=1时,y=-2,
所以当x=-1时,y有最大值6;
当x=0时,y有最小值-4.
综上,该一次函数的“友好函数”的最大值为6,最小值为-4.
(4) 由题意,画出一次函数y=2x-4的“友好函数”y=的图象如图所示.
因为直线y=b与该一次函数的“友好函数”的图象只有一个交点,
所以-4≤b≤4.
同课章节目录
