期中综合测试卷 (含答案) 2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 期中综合测试卷 (含答案) 2025-2026学年数学苏科版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 265.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 15:21:11 | ||
图片预览



文档简介
期中综合测试卷
(时间:120分钟 满分:150分)
一、 选择题(每小题3分,共24分)
1. (2025苏州工业园月考)下列实数中,是无理数的是( )
A. 3.141 592 6 B. C. - D.
2. (2025盐城射阳月考)估计的值在( )
A. 6到7之间 B. 7到8之间
C. 4到5之间 D. 8到9之间
3. (2025无锡宜兴期末)下列给出的三条线段的长,其中能组成直角三角形的是( )
A. 3,5,7 B. 6,8,9 C. 2,, D. ,,
4. 如图,在△ABC和△ABD中,AC=BD,AD=BC,则能说明△ABC≌△BAD的依据是( )
A. SSS B. ASA C. AAS D. SAS
(第4题) (第5题) (第6题) (第7题) (第8题)
5. 如图,AD是△ABC的角平分线,DE⊥AB,垂足为E.若DE=3,AC=6,则△ACD的面积为( )
A. 6 B. 18 C. 12 D. 9
6. 如图,在△ABC中,∠ABC=40°,∠ACB=60°,DE垂直平分AC,连接AE,则∠BAE的度数为( )
A. 10° B. 15° C. 20° D. 25°
7. 如图,在△ABC中,∠ABC=3∠C,AD为∠BAC的平分线,BM⊥AD,垂足为M,且AB=6,BM=2,则AC的长为( )
A. 10 B. 7 C. 8 D. 9
8. 如图,在△ABC中,∠BAC为钝角,AF,CE都是这个三角形的高,P为AC的中点.若∠B=40°,则∠EPF的度数为( )
A. 90° B. 95° C. 100° D. 105°
二、 填空题(每小题3分,共30分)
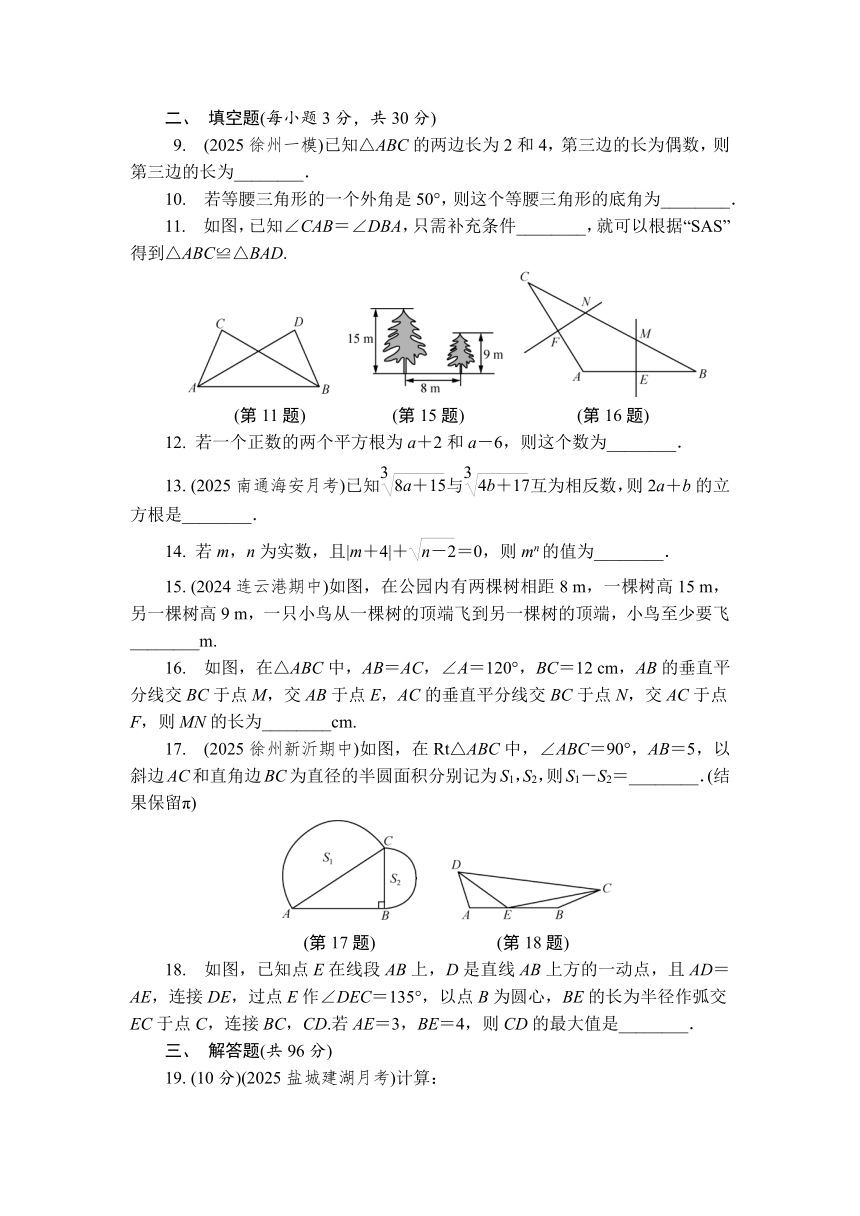
9. (2025徐州一模)已知△ABC的两边长为2和4,第三边的长为偶数,则第三边的长为________.
10. 若等腰三角形的一个外角是50°,则这个等腰三角形的底角为________.
11. 如图,已知∠CAB=∠DBA,只需补充条件________,就可以根据“SAS”得到△ABC≌△BAD.
(第11题) (第15题) (第16题)
12. 若一个正数的两个平方根为a+2和a-6,则这个数为________.
13. (2025南通海安月考)已知与互为相反数,则2a+b的立方根是________.
14. 若m,n为实数,且|m+4|+=0,则mn的值为________.
15. (2024连云港期中)如图,在公园内有两棵树相距8 m,一棵树高15 m,另一棵树高9 m,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞________m.
16. 如图,在△ABC中,AB=AC,∠A=120°,BC=12 cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为________cm.
17. (2025徐州新沂期中)如图,在Rt△ABC中,∠ABC=90°,AB=5,以斜边AC和直角边BC为直径的半圆面积分别记为S1,S2,则S1-S2=________.(结果保留π)
(第17题) (第18题)
18. 如图,已知点E在线段AB上,D是直线AB上方的一动点,且AD=AE,连接DE,过点E作∠DEC=135°,以点B为圆心,BE的长为半径作弧交EC于点C,连接BC,CD.若AE=3,BE=4,则CD的最大值是________.
三、 解答题(共96分)
19. (10分)(2025盐城建湖月考)计算:
(1) +|2-π|-; (2) -()-2+|-1|.
20. (10分)(2025盐城建湖月考)解方程:
(1) (x-1)2=16; (2) (x-3)3=32.
21. (10分)如图,已知线段AC,BD相交于点E,AE=DE,BE=CE.
(1) 求证:△ABE≌△DCE;
(2) 当AB=10时,求CD的长.
22. (10分)如图,E为△ABC的外角平分线上的一点,AE∥BC,BF=AE.求证:
(1) △ABC是等腰三角形;
(2) AF=CE.
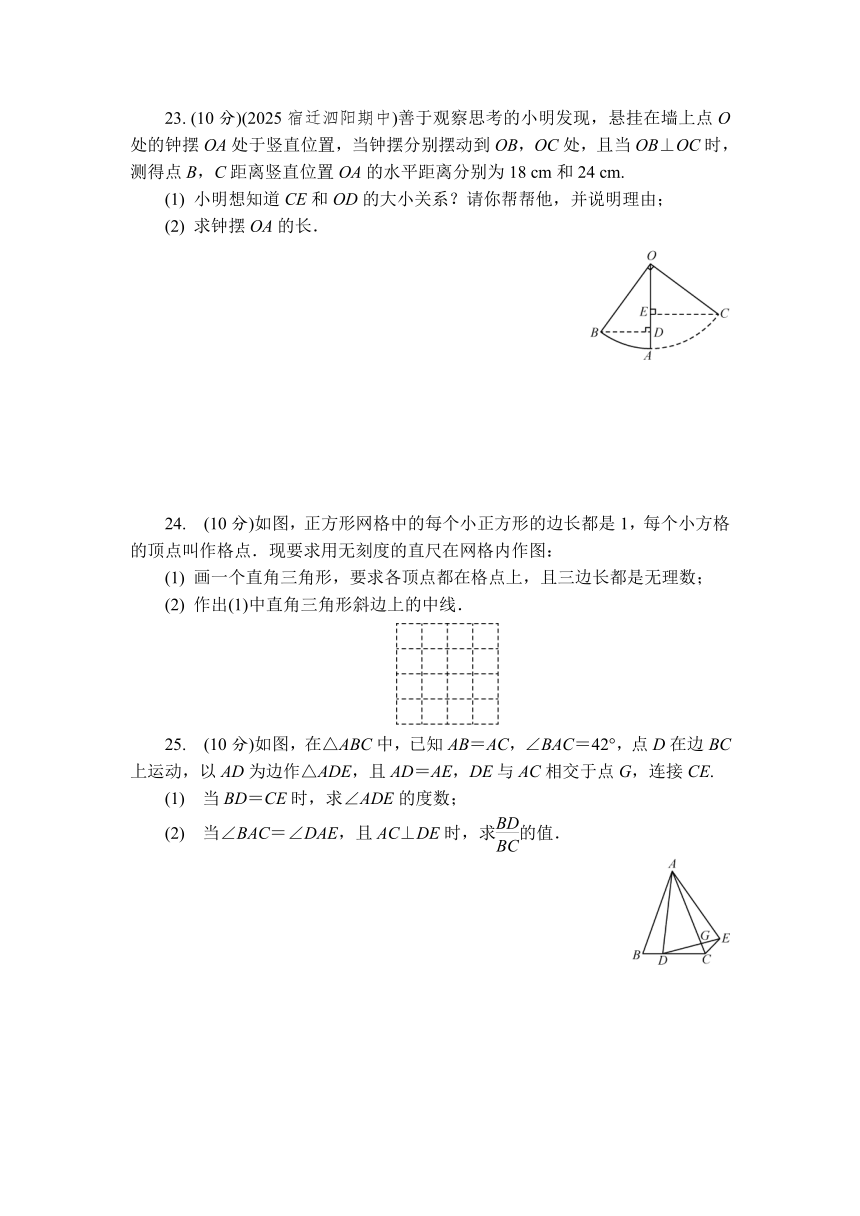
23. (10分)(2025宿迁泗阳期中)善于观察思考的小明发现,悬挂在墙上点O处的钟摆OA处于竖直位置,当钟摆分别摆动到OB,OC处,且当OB⊥OC时,测得点B,C距离竖直位置OA的水平距离分别为18 cm和24 cm.
(1) 小明想知道CE和OD的大小关系?请你帮帮他,并说明理由;
(2) 求钟摆OA的长.
24. (10分)如图,正方形网格中的每个小正方形的边长都是1,每个小方格的顶点叫作格点.现要求用无刻度的直尺在网格内作图:
(1) 画一个直角三角形,要求各顶点都在格点上,且三边长都是无理数;
(2) 作出(1)中直角三角形斜边上的中线.
25. (10分)如图,在△ABC中,已知AB=AC,∠BAC=42°,点D在边BC上运动,以AD为边作△ADE,且AD=AE,DE与AC相交于点G,连接CE.
(1) 当BD=CE时,求∠ADE的度数;
(2) 当∠BAC=∠DAE,且AC⊥DE时,求的值.
26. (12分)(2025扬州邗江期中)
【背景介绍】
勾股定理是几何学中的明珠,充满着魅力.
【知识运用】
(1) 如图,铁路上A,B两点(看作直线上的两点)相距40 km,C,D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A,B.若AD=25 km,BC=16 km,则两个村庄的距离为________km;
(2) 在(1)的条件下,若AB=40 km,AD=24 km,BC=16 km,现要在AB上建造一个供应站P,使得PC=PD,请用尺规作图在图中作出点P的位置并求出AP的距离;
【知识迁移】
(3) 借助上面的思考过程与几何模型,则代数式+(0<x<9)的最小值为________.
27. (14分)(2024常州钟楼期中)用一条直线分割一个三角形,如果能分割出等腰三角形,那么就称这条直线为该三角形的一条等腰分割线.在Rt△ABC中,∠C=90°,AC=8,BC=6.
(1) 如图1,若O为AB的中点,则直线OC________△ABC的等腰分割线(填“是”或“不是”);
(2) 如图2,已知△ABC的一条等腰分割线BP交边AC于点P,且PB=PA,求出CP的长;
(3) 如图3,在△ABC中,Q是边AB上的一点,若直线CQ是△ABC的等腰分割线,则线段BQ的长为________.
图1 图2 图3 备用图
期中综合测试卷
1. D 2. B 3. D 4. A 5. D 6. C 7. A 8. C
9. 4 10. 25° 11. AC=BD 12. 16 13. -2 14. 16
15. 10 16. 4 17. 18. 12
19. 解:(1) 原式=3+π-2-2
=3-2-2+π
=π-1.
(2) 原式=5-4+-1
=5-4-1+
=.
20. 解:(1) 因为(x-1)2=16,
所以x-1=±4,
解得x=5或x=-3.
(2) 因为(x-3)3=32,
所以(x-3)3=64,
所以x-3=4,
解得x=7.
21. (1) 证明:在△ABE和△DCE中,
所以△ABE≌△DCE(SAS).
(2) 解:因为△ABE≌△DCE,所以AB=DC.
因为AB=10,所以CD=10.
22. 证明:(1) 因为AE∥BC,
所以∠DAE=∠B,∠EAC=∠ACB.
因为E为△ABC的外角平分线上的一点,
所以∠DAE=∠EAC,
所以∠B=∠ACB,所以AB=AC,
所以△ABC是等腰三角形.
(2) 在△ABF和△CAE中,
所以△ABF≌△CAE(SAS),
所以AF=CE.
23. 解:(1) CE=OD.理由如下:
由题意可知,CE⊥OA,BD⊥OA,
所以∠CEO=∠ODB=90°,
所以∠COE+∠OCE=90°.
因为OB⊥OC,
所以∠BOC=90°,
所以∠COE+∠BOD=90°,
所以∠OCE=∠BOD.
在△COE和△OBD中,
所以△COE≌△OBD(AAS),
所以CE=OD.
(2) 由题意可知,OA=OB,BD=18 cm,CE=24 cm.
由(1)可知,OD=CE=24 cm,
在Rt△OBD中,由勾股定理,得OB===30(cm),
所以OA=30 cm,
所以钟摆OA的长为30 cm.
24. 解:(1) 如图1,△ABC即为所求.(答案不唯一)
(2) 如图2,取格点D,E,连接DE与AB,交于点F,连接CF,则CF即为所求.(答案不唯一)
图1 图2
25. 解:(1) 在△ABD和△ACE中,
所以△ABD≌△ACE(SSS),
所以∠BAD=∠CAE,
所以∠BAC=∠DAE=42°.
因为AD=AE,
所以∠ADE=×(180°-42°)=69°.
(2) 因为∠BAC=∠DAE,
所以∠BAD=∠CAE.
在△ABD和△ACE中,
所以△ABD≌△ACE(SAS),所以BD=CE.
因为AD=AE,AC⊥DE,
所以AC垂直平分DE,
所以CD=CE,所以BD=CD,
所以BC=BD+CD=2BD,所以=.
26. 解:(1) 41 提示:如图1,连接CD,作CE⊥AD于点E.因为AD⊥AB,BC⊥AB,所以BC=AE,CE=AB,所以DE=AD-AE=25-16=9(km),所以CD===41(km).故两个村庄相距41 km.
(2) 如图2,设AP=x km,则BP=(40-x) km,
在Rt△ADP中,DP2=AP2+AD2=x2+242,
在Rt△BPC中,CP2=BP2+BC2=(40-x)2+162.
因为PC=PD,
所以x2+242=(40-x)2+162,
解得x=16,所以AP=16 km.
(3) 15 提示:如图3,先作出点C关于AB的对称点F,连接DF,过点F作EF⊥AD交AD的延长线于点E,则DF就是代数式+(0<x<9)的最小值.代数式+(0<x<9)的几何意义是线段AB上一点到点D,C的距离之和,而它的最小值就是点C的对称点F和点D的距离,所以最小值为==15.
图1 图2 图3
27. 解:(1) 是
(2) 由题意可知PA=PB,BC=6,
设CP=x,则PA=PB=8-x,
在Rt△BPC中,BC2+PC2=PB2,
所以62+x2=(8-x)2,
解得x=,
所以CP=.
(3) 5或2或6或 提示:若△ACQ为等腰三角形,如图1,当AC=AQ时,AQ=8,BQ=AB-AQ=2;如图2,当QC=QA时,Q为AB的中点,BQ=AB=5;当CA=CQ时,点Q不在线段AB上,故舍去;若△BCQ为等腰三角形,如图3,当CQ=CB时,过点C作CM⊥AB于点M,此时M为BQ的中点,所以S△ABC=BC·AC=AB·CM,即×6×8=×10CM,解得CM=.在Rt△CMQ中,由勾股定理,得BM==,所以BQ=2QM=;如图4,当BC=BQ时,BQ=BC=6;如图5,当QC=QB时,Q为AB的中点,BQ=AB=5.综上,BQ=2或BQ=5或BQ=或BQ=6.
图1 图2 图3 图4 图5
(时间:120分钟 满分:150分)
一、 选择题(每小题3分,共24分)
1. (2025苏州工业园月考)下列实数中,是无理数的是( )
A. 3.141 592 6 B. C. - D.
2. (2025盐城射阳月考)估计的值在( )
A. 6到7之间 B. 7到8之间
C. 4到5之间 D. 8到9之间
3. (2025无锡宜兴期末)下列给出的三条线段的长,其中能组成直角三角形的是( )
A. 3,5,7 B. 6,8,9 C. 2,, D. ,,
4. 如图,在△ABC和△ABD中,AC=BD,AD=BC,则能说明△ABC≌△BAD的依据是( )
A. SSS B. ASA C. AAS D. SAS
(第4题) (第5题) (第6题) (第7题) (第8题)
5. 如图,AD是△ABC的角平分线,DE⊥AB,垂足为E.若DE=3,AC=6,则△ACD的面积为( )
A. 6 B. 18 C. 12 D. 9
6. 如图,在△ABC中,∠ABC=40°,∠ACB=60°,DE垂直平分AC,连接AE,则∠BAE的度数为( )
A. 10° B. 15° C. 20° D. 25°
7. 如图,在△ABC中,∠ABC=3∠C,AD为∠BAC的平分线,BM⊥AD,垂足为M,且AB=6,BM=2,则AC的长为( )
A. 10 B. 7 C. 8 D. 9
8. 如图,在△ABC中,∠BAC为钝角,AF,CE都是这个三角形的高,P为AC的中点.若∠B=40°,则∠EPF的度数为( )
A. 90° B. 95° C. 100° D. 105°
二、 填空题(每小题3分,共30分)
9. (2025徐州一模)已知△ABC的两边长为2和4,第三边的长为偶数,则第三边的长为________.
10. 若等腰三角形的一个外角是50°,则这个等腰三角形的底角为________.
11. 如图,已知∠CAB=∠DBA,只需补充条件________,就可以根据“SAS”得到△ABC≌△BAD.
(第11题) (第15题) (第16题)
12. 若一个正数的两个平方根为a+2和a-6,则这个数为________.
13. (2025南通海安月考)已知与互为相反数,则2a+b的立方根是________.
14. 若m,n为实数,且|m+4|+=0,则mn的值为________.
15. (2024连云港期中)如图,在公园内有两棵树相距8 m,一棵树高15 m,另一棵树高9 m,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞________m.
16. 如图,在△ABC中,AB=AC,∠A=120°,BC=12 cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为________cm.
17. (2025徐州新沂期中)如图,在Rt△ABC中,∠ABC=90°,AB=5,以斜边AC和直角边BC为直径的半圆面积分别记为S1,S2,则S1-S2=________.(结果保留π)
(第17题) (第18题)
18. 如图,已知点E在线段AB上,D是直线AB上方的一动点,且AD=AE,连接DE,过点E作∠DEC=135°,以点B为圆心,BE的长为半径作弧交EC于点C,连接BC,CD.若AE=3,BE=4,则CD的最大值是________.
三、 解答题(共96分)
19. (10分)(2025盐城建湖月考)计算:
(1) +|2-π|-; (2) -()-2+|-1|.
20. (10分)(2025盐城建湖月考)解方程:
(1) (x-1)2=16; (2) (x-3)3=32.
21. (10分)如图,已知线段AC,BD相交于点E,AE=DE,BE=CE.
(1) 求证:△ABE≌△DCE;
(2) 当AB=10时,求CD的长.
22. (10分)如图,E为△ABC的外角平分线上的一点,AE∥BC,BF=AE.求证:
(1) △ABC是等腰三角形;
(2) AF=CE.
23. (10分)(2025宿迁泗阳期中)善于观察思考的小明发现,悬挂在墙上点O处的钟摆OA处于竖直位置,当钟摆分别摆动到OB,OC处,且当OB⊥OC时,测得点B,C距离竖直位置OA的水平距离分别为18 cm和24 cm.
(1) 小明想知道CE和OD的大小关系?请你帮帮他,并说明理由;
(2) 求钟摆OA的长.
24. (10分)如图,正方形网格中的每个小正方形的边长都是1,每个小方格的顶点叫作格点.现要求用无刻度的直尺在网格内作图:
(1) 画一个直角三角形,要求各顶点都在格点上,且三边长都是无理数;
(2) 作出(1)中直角三角形斜边上的中线.
25. (10分)如图,在△ABC中,已知AB=AC,∠BAC=42°,点D在边BC上运动,以AD为边作△ADE,且AD=AE,DE与AC相交于点G,连接CE.
(1) 当BD=CE时,求∠ADE的度数;
(2) 当∠BAC=∠DAE,且AC⊥DE时,求的值.
26. (12分)(2025扬州邗江期中)
【背景介绍】
勾股定理是几何学中的明珠,充满着魅力.
【知识运用】
(1) 如图,铁路上A,B两点(看作直线上的两点)相距40 km,C,D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A,B.若AD=25 km,BC=16 km,则两个村庄的距离为________km;
(2) 在(1)的条件下,若AB=40 km,AD=24 km,BC=16 km,现要在AB上建造一个供应站P,使得PC=PD,请用尺规作图在图中作出点P的位置并求出AP的距离;
【知识迁移】
(3) 借助上面的思考过程与几何模型,则代数式+(0<x<9)的最小值为________.
27. (14分)(2024常州钟楼期中)用一条直线分割一个三角形,如果能分割出等腰三角形,那么就称这条直线为该三角形的一条等腰分割线.在Rt△ABC中,∠C=90°,AC=8,BC=6.
(1) 如图1,若O为AB的中点,则直线OC________△ABC的等腰分割线(填“是”或“不是”);
(2) 如图2,已知△ABC的一条等腰分割线BP交边AC于点P,且PB=PA,求出CP的长;
(3) 如图3,在△ABC中,Q是边AB上的一点,若直线CQ是△ABC的等腰分割线,则线段BQ的长为________.
图1 图2 图3 备用图
期中综合测试卷
1. D 2. B 3. D 4. A 5. D 6. C 7. A 8. C
9. 4 10. 25° 11. AC=BD 12. 16 13. -2 14. 16
15. 10 16. 4 17. 18. 12
19. 解:(1) 原式=3+π-2-2
=3-2-2+π
=π-1.
(2) 原式=5-4+-1
=5-4-1+
=.
20. 解:(1) 因为(x-1)2=16,
所以x-1=±4,
解得x=5或x=-3.
(2) 因为(x-3)3=32,
所以(x-3)3=64,
所以x-3=4,
解得x=7.
21. (1) 证明:在△ABE和△DCE中,
所以△ABE≌△DCE(SAS).
(2) 解:因为△ABE≌△DCE,所以AB=DC.
因为AB=10,所以CD=10.
22. 证明:(1) 因为AE∥BC,
所以∠DAE=∠B,∠EAC=∠ACB.
因为E为△ABC的外角平分线上的一点,
所以∠DAE=∠EAC,
所以∠B=∠ACB,所以AB=AC,
所以△ABC是等腰三角形.
(2) 在△ABF和△CAE中,
所以△ABF≌△CAE(SAS),
所以AF=CE.
23. 解:(1) CE=OD.理由如下:
由题意可知,CE⊥OA,BD⊥OA,
所以∠CEO=∠ODB=90°,
所以∠COE+∠OCE=90°.
因为OB⊥OC,
所以∠BOC=90°,
所以∠COE+∠BOD=90°,
所以∠OCE=∠BOD.
在△COE和△OBD中,
所以△COE≌△OBD(AAS),
所以CE=OD.
(2) 由题意可知,OA=OB,BD=18 cm,CE=24 cm.
由(1)可知,OD=CE=24 cm,
在Rt△OBD中,由勾股定理,得OB===30(cm),
所以OA=30 cm,
所以钟摆OA的长为30 cm.
24. 解:(1) 如图1,△ABC即为所求.(答案不唯一)
(2) 如图2,取格点D,E,连接DE与AB,交于点F,连接CF,则CF即为所求.(答案不唯一)
图1 图2
25. 解:(1) 在△ABD和△ACE中,
所以△ABD≌△ACE(SSS),
所以∠BAD=∠CAE,
所以∠BAC=∠DAE=42°.
因为AD=AE,
所以∠ADE=×(180°-42°)=69°.
(2) 因为∠BAC=∠DAE,
所以∠BAD=∠CAE.
在△ABD和△ACE中,
所以△ABD≌△ACE(SAS),所以BD=CE.
因为AD=AE,AC⊥DE,
所以AC垂直平分DE,
所以CD=CE,所以BD=CD,
所以BC=BD+CD=2BD,所以=.
26. 解:(1) 41 提示:如图1,连接CD,作CE⊥AD于点E.因为AD⊥AB,BC⊥AB,所以BC=AE,CE=AB,所以DE=AD-AE=25-16=9(km),所以CD===41(km).故两个村庄相距41 km.
(2) 如图2,设AP=x km,则BP=(40-x) km,
在Rt△ADP中,DP2=AP2+AD2=x2+242,
在Rt△BPC中,CP2=BP2+BC2=(40-x)2+162.
因为PC=PD,
所以x2+242=(40-x)2+162,
解得x=16,所以AP=16 km.
(3) 15 提示:如图3,先作出点C关于AB的对称点F,连接DF,过点F作EF⊥AD交AD的延长线于点E,则DF就是代数式+(0<x<9)的最小值.代数式+(0<x<9)的几何意义是线段AB上一点到点D,C的距离之和,而它的最小值就是点C的对称点F和点D的距离,所以最小值为==15.
图1 图2 图3
27. 解:(1) 是
(2) 由题意可知PA=PB,BC=6,
设CP=x,则PA=PB=8-x,
在Rt△BPC中,BC2+PC2=PB2,
所以62+x2=(8-x)2,
解得x=,
所以CP=.
(3) 5或2或6或 提示:若△ACQ为等腰三角形,如图1,当AC=AQ时,AQ=8,BQ=AB-AQ=2;如图2,当QC=QA时,Q为AB的中点,BQ=AB=5;当CA=CQ时,点Q不在线段AB上,故舍去;若△BCQ为等腰三角形,如图3,当CQ=CB时,过点C作CM⊥AB于点M,此时M为BQ的中点,所以S△ABC=BC·AC=AB·CM,即×6×8=×10CM,解得CM=.在Rt△CMQ中,由勾股定理,得BM==,所以BQ=2QM=;如图4,当BC=BQ时,BQ=BC=6;如图5,当QC=QB时,Q为AB的中点,BQ=AB=5.综上,BQ=2或BQ=5或BQ=或BQ=6.
图1 图2 图3 图4 图5
同课章节目录
