微专题9求一次函数表达式的六种类型 同步练(含答案) 2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 微专题9求一次函数表达式的六种类型 同步练(含答案) 2025-2026学年数学苏科版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 87.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 21:43:02 | ||
图片预览


文档简介
微专题9 求一次函数表达式的六种类型
类型一 根据定义求表达式
1 已知函数y=(m-2)xm2-3-5是一次函数,则m= .
2 已知函数y=(m+1)xm2-3是正比例函数,且图象在第二、四象限内,则m的值是 .
类型二 根据待定系数法求函数表达式
3 (2024盐城建湖期末)已知y与x-2成正比例,且当x=1时,y=-3.
(1) 求y与x的函数表达式;
(2) 若点(m,-9)在该函数的图象上,求m的值.
4 已知y是x的一次函数,当x=3时,y=1;当x=-2时,y=-4.
(1) 求这个函数的表达式;
(2) 当x为何值时,函数y的值为-1
类型三 根据一次函数的性质求函数表达式
5 已知一次函数y=kx+b,当-1≤x≤5时,-1≤y≤11,求这个一次函数的表达式.
6 如图,直线l1:y=k1x+6与直线l2:y=k2x+b相交于点A(-3,3),l1交y轴于点B,l2交y轴负半轴于点C,且OB=2OC.
(1) 求直线l1和l2的表达式;
(2) 若D是直线l1上的一点,且△BCD的面积是9,求点D的坐标.
类型四 根据平移求函数表达式
7 (2024南京期末)将y=2x+3的图象向下平移4个单位长度,所得图象对应的函数表达式是 .
8 (2024无锡期末)如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(2,0)和B(0,-4).
(1) 求这个一次函数的表达式;
(2) 将直线AB向上平移6个单位长度,求平移后的直线与坐标轴围成的三角形的面积.
类型五 根据旋转求函数表达式
9 (2024苏州)已知直线l1:y=x-1与x轴交于点A,将直线l1绕点A按逆时针方向旋转15°,得到直线l2,则直线l2对应的函数表达式是 .
10 如图,一次函数y=-2x+4的图象与y轴的交点为A,将直线y=-2x+4绕点A按逆时针方向旋转45°,求所得的图象对应的函数表达式.
11 (1) 【模型建立】
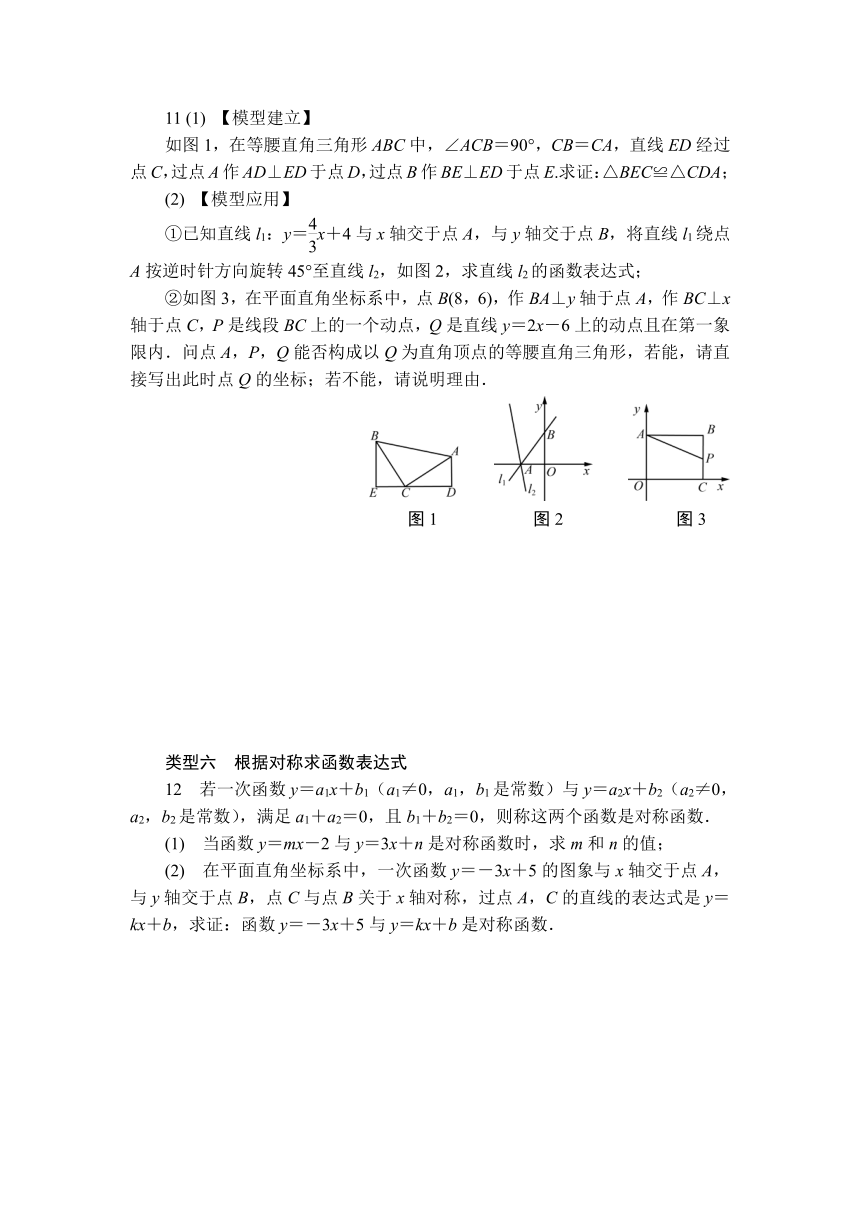
如图1,在等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E.求证:△BEC≌△CDA;
(2) 【模型应用】
①已知直线l1:y=x+4与x轴交于点A,与y轴交于点B,将直线l1绕点A按逆时针方向旋转45°至直线l2,如图2,求直线l2的函数表达式;
②如图3,在平面直角坐标系中,点B(8,6),作BA⊥y轴于点A,作BC⊥x轴于点C,P是线段BC上的一个动点,Q是直线y=2x-6上的动点且在第一象限内.问点A,P,Q能否构成以Q为直角顶点的等腰直角三角形,若能,请直接写出此时点Q的坐标;若不能,请说明理由.
图1 图2 图3
类型六 根据对称求函数表达式
12 若一次函数y=a1x+b1(a1≠0,a1,b1是常数)与y=a2x+b2(a2≠0,a2,b2是常数),满足a1+a2=0,且b1+b2=0,则称这两个函数是对称函数.
(1) 当函数y=mx-2与y=3x+n是对称函数时,求m和n的值;
(2) 在平面直角坐标系中,一次函数y=-3x+5的图象与x轴交于点A,与y轴交于点B,点C与点B关于x轴对称,过点A,C的直线的表达式是y=kx+b,求证:函数y=-3x+5与y=kx+b是对称函数.
微专题9 求一次函数表达式的六种类型
1. -2 2. -2
3. 解:(1) 由y与x-2成正比例,设y=k(x-2).
因为当x=1时,y=-3,
所以-3=k×(1-2),解得k=3,
所以y=3(x-2)=3x-6,
所以y与x的函数表达式为y=3x-6.
(2) 因为点(m,-9)在该函数的图象上,
所以-9=3m-6,解得m=-1,
所以m的值是-1.
4. 解:(1) 设一次函数的表达式为y=kx+b.
根据题意,得解得
所以这个函数的表达式为y=x-2.
(2) 当y=-1时,x-2=-1,解得x=1,
所以当x的值为1时,函数y的值为-1.
5. 解:若当x=-1时,y=-1;当x=5时,y=11,
则解得
所以此时一次函数的表达式为y=2x+1;
若当x=-1时,y=11;当x=5时,y=-1,
则解得
所以此时一次函数的表达式为y=-2x+9.
综上所述,一次函数的表达式为y=-2x+9或y=2x+1.
6. 解:(1) 将点A(-3,3)的坐标代入y=k1x+6,
得-3k1+6=3,解得k1=1,
所以直线l1的表达式为y=x+6.
令x=0,则y=6,所以B(0,6).
因为OB=2OC,且点C位于y轴负半轴,所以C(0,-3).
将点 A(-3,3),C(0,-3)的坐标代入y=k2x+b,
得解得
所以直线l2的表达式为y=-2x-3.
(2) 设点D到y轴的距离为m,则×9×m=9,
所以m=2.
在直线l1:y=x+6中,当x=2时,y=2+6=8;
当x=-2时,y=-2+6=4,
所以点D的坐标为(2,8)或(-2,4).
7. y=2x-1
8. 解:(1) 因为一次函数y=kx+b的图象经过点A(2,0)和B(0,-4),
所以解得
所以一次函数的表达式为y=2x-4.
(2) 因为一次函数的表达式为y=2x-4,
所以直线AB向上平移6个单位长度后所得直线的表达式为y=2x+2.
因为当x=0时,y=2;当y=0时,x=-1,
所以直线与坐标轴的交点为(0,2),(-1,0),
所以平移后的直线与坐标轴围成的三角形的面积为×2×1=1.
9. y=x-
10. 解:过点B作BD⊥AB交旋转所得的图象于点D,过点D作DE⊥x轴于点E.
在y=-2x+4中,令x=0,得y=4,所以点A(0,4),
所以OA=4.
令y=0,得x=2,所以点B(2,0),所以OB=2.
因为将直线y=-2x+4绕点A按逆时针方向旋转45°,所以∠BAD=45°,所以AB=BD.
因为∠ABD=90°,所以∠ABO+∠DBE=90°.
因为∠AOB=90°,所以∠ABO+∠OAB=90°,
所以∠DBE=∠OAB.
在△AOB和△BED中,
所以△AOB≌△BED(AAS),
所以BE=OA=4,DE=OB=2,
所以OE=OB+BE=6,所以点D(6,2).
设所得的图象对应的函数表达式为y=kx+b,
将点A(0,4),D(6,2)的坐标代入y=kx+b,
得解得
所以所得的图象对应的函数表达式为y=-x+4.
11. 解:(1) 因为△ABC为等腰直角三角形,
所以CB=CA,∠ACD+∠BCE=180°-90°=90°.
又因为AD⊥CD,BE⊥EC,
所以∠D=∠E=90°.
又因为∠CBE+∠BCE=90°,
所以∠ACD=∠CBE.
在△ACD与△CBE中,
所以△BEC≌△CDA(AAS).
(2) ①如图,过点B作BC⊥AB交l2于点C,过点C作CD⊥y轴于点D.
因为∠BAC=45°,
所以△ABC为等腰直角三角形.
由(1)可知,△CBD≌△BAO,
所以BD=AO,CD=BO.
因为直线l1:y=x+4,
令y=0,则x=-3,
所以A(-3,0);
令x=0,则y=4,
所以B(0,4),
所以BD=AO=3,CD=OB=4,
所以OD=4+3=7,
所以C(-4,7).
设直线l2的函数表达式为y=kx+b.
将点A(-3,0),C(-4,7)代入y=kx+b中,
得
解得k=-7,b=-21,
所以直线l2的函数表达式为y=-7x-21.
②Q(4,2)或(,).
12. 解:(1) 因为函数y=mx-2与y=3x+n是对称函数,
所以解得
(2) 对于一次函数y=-3x+5,
令x=0,得y=5;令y=0,得x=,
所以点A(,0),B(0,5).
因为点C与点B关于x轴对称,所以点C(0,-5).
将点A(,0)与C(0,-5)的坐标代入y=kx+b,
得解得
所以直线AC的表达式为y=3x-5.
因为-3+3=0,5+(-5)=0,
所以函数y=-3x+5与y=kx+b是对称函数.
类型一 根据定义求表达式
1 已知函数y=(m-2)xm2-3-5是一次函数,则m= .
2 已知函数y=(m+1)xm2-3是正比例函数,且图象在第二、四象限内,则m的值是 .
类型二 根据待定系数法求函数表达式
3 (2024盐城建湖期末)已知y与x-2成正比例,且当x=1时,y=-3.
(1) 求y与x的函数表达式;
(2) 若点(m,-9)在该函数的图象上,求m的值.
4 已知y是x的一次函数,当x=3时,y=1;当x=-2时,y=-4.
(1) 求这个函数的表达式;
(2) 当x为何值时,函数y的值为-1
类型三 根据一次函数的性质求函数表达式
5 已知一次函数y=kx+b,当-1≤x≤5时,-1≤y≤11,求这个一次函数的表达式.
6 如图,直线l1:y=k1x+6与直线l2:y=k2x+b相交于点A(-3,3),l1交y轴于点B,l2交y轴负半轴于点C,且OB=2OC.
(1) 求直线l1和l2的表达式;
(2) 若D是直线l1上的一点,且△BCD的面积是9,求点D的坐标.
类型四 根据平移求函数表达式
7 (2024南京期末)将y=2x+3的图象向下平移4个单位长度,所得图象对应的函数表达式是 .
8 (2024无锡期末)如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(2,0)和B(0,-4).
(1) 求这个一次函数的表达式;
(2) 将直线AB向上平移6个单位长度,求平移后的直线与坐标轴围成的三角形的面积.
类型五 根据旋转求函数表达式
9 (2024苏州)已知直线l1:y=x-1与x轴交于点A,将直线l1绕点A按逆时针方向旋转15°,得到直线l2,则直线l2对应的函数表达式是 .
10 如图,一次函数y=-2x+4的图象与y轴的交点为A,将直线y=-2x+4绕点A按逆时针方向旋转45°,求所得的图象对应的函数表达式.
11 (1) 【模型建立】
如图1,在等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E.求证:△BEC≌△CDA;
(2) 【模型应用】
①已知直线l1:y=x+4与x轴交于点A,与y轴交于点B,将直线l1绕点A按逆时针方向旋转45°至直线l2,如图2,求直线l2的函数表达式;
②如图3,在平面直角坐标系中,点B(8,6),作BA⊥y轴于点A,作BC⊥x轴于点C,P是线段BC上的一个动点,Q是直线y=2x-6上的动点且在第一象限内.问点A,P,Q能否构成以Q为直角顶点的等腰直角三角形,若能,请直接写出此时点Q的坐标;若不能,请说明理由.
图1 图2 图3
类型六 根据对称求函数表达式
12 若一次函数y=a1x+b1(a1≠0,a1,b1是常数)与y=a2x+b2(a2≠0,a2,b2是常数),满足a1+a2=0,且b1+b2=0,则称这两个函数是对称函数.
(1) 当函数y=mx-2与y=3x+n是对称函数时,求m和n的值;
(2) 在平面直角坐标系中,一次函数y=-3x+5的图象与x轴交于点A,与y轴交于点B,点C与点B关于x轴对称,过点A,C的直线的表达式是y=kx+b,求证:函数y=-3x+5与y=kx+b是对称函数.
微专题9 求一次函数表达式的六种类型
1. -2 2. -2
3. 解:(1) 由y与x-2成正比例,设y=k(x-2).
因为当x=1时,y=-3,
所以-3=k×(1-2),解得k=3,
所以y=3(x-2)=3x-6,
所以y与x的函数表达式为y=3x-6.
(2) 因为点(m,-9)在该函数的图象上,
所以-9=3m-6,解得m=-1,
所以m的值是-1.
4. 解:(1) 设一次函数的表达式为y=kx+b.
根据题意,得解得
所以这个函数的表达式为y=x-2.
(2) 当y=-1时,x-2=-1,解得x=1,
所以当x的值为1时,函数y的值为-1.
5. 解:若当x=-1时,y=-1;当x=5时,y=11,
则解得
所以此时一次函数的表达式为y=2x+1;
若当x=-1时,y=11;当x=5时,y=-1,
则解得
所以此时一次函数的表达式为y=-2x+9.
综上所述,一次函数的表达式为y=-2x+9或y=2x+1.
6. 解:(1) 将点A(-3,3)的坐标代入y=k1x+6,
得-3k1+6=3,解得k1=1,
所以直线l1的表达式为y=x+6.
令x=0,则y=6,所以B(0,6).
因为OB=2OC,且点C位于y轴负半轴,所以C(0,-3).
将点 A(-3,3),C(0,-3)的坐标代入y=k2x+b,
得解得
所以直线l2的表达式为y=-2x-3.
(2) 设点D到y轴的距离为m,则×9×m=9,
所以m=2.
在直线l1:y=x+6中,当x=2时,y=2+6=8;
当x=-2时,y=-2+6=4,
所以点D的坐标为(2,8)或(-2,4).
7. y=2x-1
8. 解:(1) 因为一次函数y=kx+b的图象经过点A(2,0)和B(0,-4),
所以解得
所以一次函数的表达式为y=2x-4.
(2) 因为一次函数的表达式为y=2x-4,
所以直线AB向上平移6个单位长度后所得直线的表达式为y=2x+2.
因为当x=0时,y=2;当y=0时,x=-1,
所以直线与坐标轴的交点为(0,2),(-1,0),
所以平移后的直线与坐标轴围成的三角形的面积为×2×1=1.
9. y=x-
10. 解:过点B作BD⊥AB交旋转所得的图象于点D,过点D作DE⊥x轴于点E.
在y=-2x+4中,令x=0,得y=4,所以点A(0,4),
所以OA=4.
令y=0,得x=2,所以点B(2,0),所以OB=2.
因为将直线y=-2x+4绕点A按逆时针方向旋转45°,所以∠BAD=45°,所以AB=BD.
因为∠ABD=90°,所以∠ABO+∠DBE=90°.
因为∠AOB=90°,所以∠ABO+∠OAB=90°,
所以∠DBE=∠OAB.
在△AOB和△BED中,
所以△AOB≌△BED(AAS),
所以BE=OA=4,DE=OB=2,
所以OE=OB+BE=6,所以点D(6,2).
设所得的图象对应的函数表达式为y=kx+b,
将点A(0,4),D(6,2)的坐标代入y=kx+b,
得解得
所以所得的图象对应的函数表达式为y=-x+4.
11. 解:(1) 因为△ABC为等腰直角三角形,
所以CB=CA,∠ACD+∠BCE=180°-90°=90°.
又因为AD⊥CD,BE⊥EC,
所以∠D=∠E=90°.
又因为∠CBE+∠BCE=90°,
所以∠ACD=∠CBE.
在△ACD与△CBE中,
所以△BEC≌△CDA(AAS).
(2) ①如图,过点B作BC⊥AB交l2于点C,过点C作CD⊥y轴于点D.
因为∠BAC=45°,
所以△ABC为等腰直角三角形.
由(1)可知,△CBD≌△BAO,
所以BD=AO,CD=BO.
因为直线l1:y=x+4,
令y=0,则x=-3,
所以A(-3,0);
令x=0,则y=4,
所以B(0,4),
所以BD=AO=3,CD=OB=4,
所以OD=4+3=7,
所以C(-4,7).
设直线l2的函数表达式为y=kx+b.
将点A(-3,0),C(-4,7)代入y=kx+b中,
得
解得k=-7,b=-21,
所以直线l2的函数表达式为y=-7x-21.
②Q(4,2)或(,).
12. 解:(1) 因为函数y=mx-2与y=3x+n是对称函数,
所以解得
(2) 对于一次函数y=-3x+5,
令x=0,得y=5;令y=0,得x=,
所以点A(,0),B(0,5).
因为点C与点B关于x轴对称,所以点C(0,-5).
将点A(,0)与C(0,-5)的坐标代入y=kx+b,
得解得
所以直线AC的表达式为y=3x-5.
因为-3+3=0,5+(-5)=0,
所以函数y=-3x+5与y=kx+b是对称函数.
同课章节目录
