1.2 全等三角形 同步练 (含答案)2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 1.2 全等三角形 同步练 (含答案)2025-2026学年数学苏科版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 199.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 15:21:40 | ||
图片预览

文档简介
1.2 全等三角形
1. 理解全等三角形的概念,并能识别对应边、对应角.
2. 掌握全等三角形的性质,并能进行简单的推理和计算.
建议用时:15分钟
1 (2025扬州邗江期末)如图,△ABC≌△FED,则下列结论中错误的是( )
A. DF=BD B. EF∥AB C. EC=BD D. AC∥FD
(第1题) (第2题) (第3题) (第4题)
2 已知图中的两个三角形全等,则∠α的度数是( )
A. 72° B. 60° C. 58° D. 50°
3 如图,已知图中有两对三角形全等.
(1) △ABM≌________,在这两个全等三角形中,AB的对应边是________,BM的对应边是________,MA的对应边是________;
(2) △ABN≌________,在这两个全等三角形中,∠BAN的对应角是________,∠B的对应角是________,∠ANB的对应角是________.
4 (2025泰州海陵期末)如图,点E,F分别在线段AC,AB上,若△ABE≌△ACF,且AB=10,AE=4,则EC的长为________.
5 (2025盐城月考)如图,点A,B,C,D在同一直线上,△ACE≌△DBF,AD=8,BC=2.
(1) 求AC的长;
(2) 求证:AE∥DF.
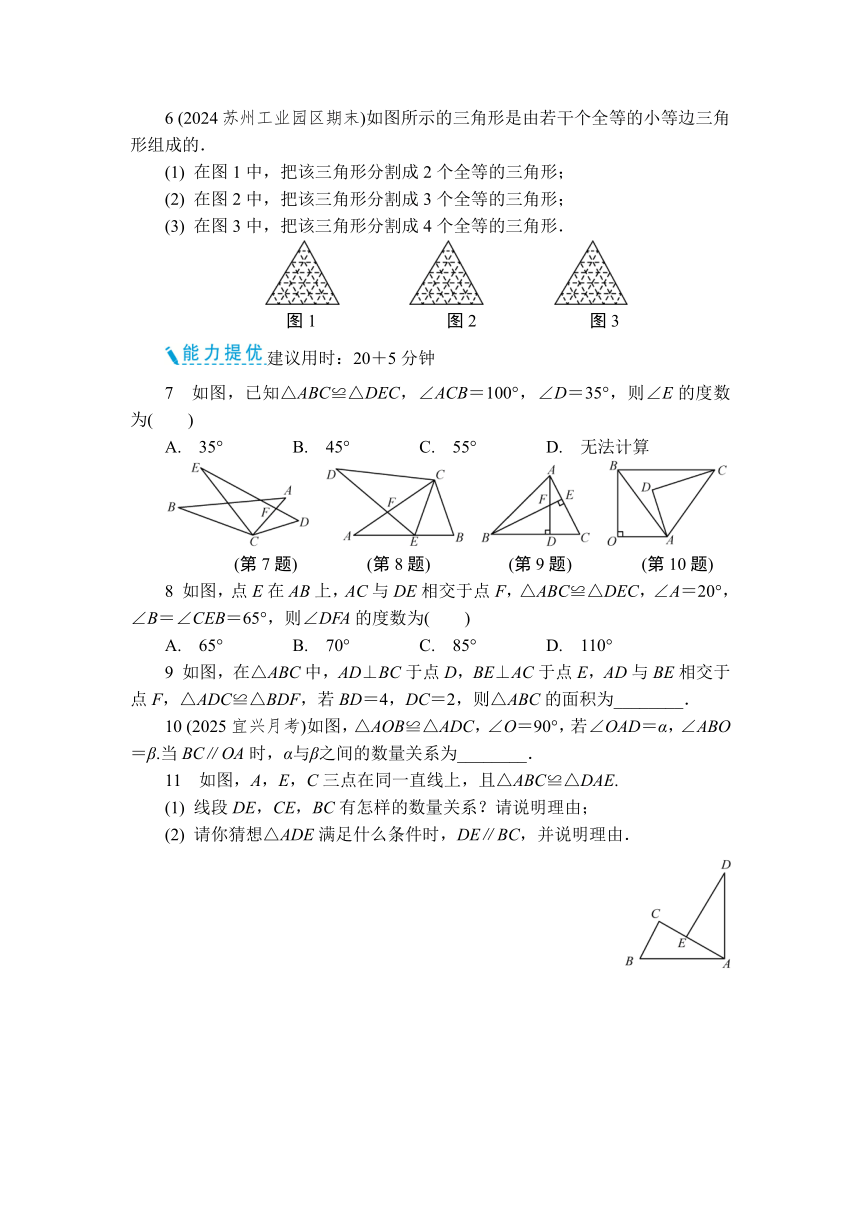
6 (2024苏州工业园区期末)如图所示的三角形是由若干个全等的小等边三角形组成的.
(1) 在图1中,把该三角形分割成2个全等的三角形;
(2) 在图2中,把该三角形分割成3个全等的三角形;
(3) 在图3中,把该三角形分割成4个全等的三角形.
图1 图2 图3
建议用时:20+5分钟
7 如图,已知△ABC≌△DEC,∠ACB=100°,∠D=35°,则∠E的度数为( )
A. 35° B. 45° C. 55° D. 无法计算
(第7题) (第8题) (第9题) (第10题)
8 如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠A=20°,∠B=∠CEB=65°,则∠DFA的度数为( )
A. 65° B. 70° C. 85° D. 110°
9 如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE相交于点F,△ADC≌△BDF,若BD=4,DC=2,则△ABC的面积为________.
10 (2025宜兴月考)如图,△AOB≌△ADC,∠O=90°,若∠OAD=α,∠ABO=β.当BC∥OA时,α与β之间的数量关系为________.
11 如图,A,E,C三点在同一直线上,且△ABC≌△DAE.
(1) 线段DE,CE,BC有怎样的数量关系?请说明理由;
(2) 请你猜想△ADE满足什么条件时,DE∥BC,并说明理由.
12 (2025广陵月考)如图,在△ABC中,AB=AC=24 cm,BC=16 cm,D为AB的中点.如果点P在线段BC上以4 cm/s的速度由点B向点C运动.同时,点Q在线段CA上以a cm/s的速度由点C向A点运动,设运动的时间为t s.
(1) ①BP=________cm;②CP=________cm;③CQ=________cm;(用含t,a的式子表示)
(2) 若以D,B,P为顶点的三角形和以P,C,Q为顶点的三角形全等,求a,t的值.
1.2 全等三角形
1. A 2. D 3. (1) △ACN AC CN NA
(2) △ACM ∠CAM ∠C ∠AMC 4. 6
5. (1) 解:因为△ACE≌△DBF,
所以AC=DB.
因为AC+BD=AD+BC,
所以2AC=AD+BC.
因为AD=8,BC=2,
所以2AC=8+2=10,
所以AC=5.
(2) 证明:因为△ACE≌△DBF,
所以∠A=∠D,
所以AE∥DF.
6. 解:(1) 如图1,作高,图1即为所求.
(2) 如图2,作角平分线,图2即为所求.
(3) 如图3,连接各边中点,图3即为所求.
图1 图2 图3
7. B 8. B 9. 12 10. α=2β
11. 解: (1) DE=CE+BC.理由如下:
因为△ABC≌△DAE,
所以AE=BC,DE=AC.
因为A,E,C三点在同一直线上,
所以AC=AE+CE,
所以DE=CE+BC.
(2) 当△ADE满足∠AED=90°时,DE∥BC.理由如下:
因为△ABC≌△DAE,∠AED=90°,
所以∠C=∠AED=90°,∠DEC=180°-∠AED=90°,
所以∠C=∠DEC,
所以DE∥BC,
即当△ADE满足∠AED=90°时,DE∥BC.
12. 解:(1) 4t 16-4t at
(2) 因为BP=4t cm,BD=12 cm,CP=(16-4t) cm,CQ=at cm,
所以∠B=∠C,
可分为两种情况,
①若△DBP≌△QCP,
则
所以
所以
②若△DBP≌△PCQ,
则
所以
所以
综上,a的值为6,t的值为2或a的值为4,t的值为1.
1. 理解全等三角形的概念,并能识别对应边、对应角.
2. 掌握全等三角形的性质,并能进行简单的推理和计算.
建议用时:15分钟
1 (2025扬州邗江期末)如图,△ABC≌△FED,则下列结论中错误的是( )
A. DF=BD B. EF∥AB C. EC=BD D. AC∥FD
(第1题) (第2题) (第3题) (第4题)
2 已知图中的两个三角形全等,则∠α的度数是( )
A. 72° B. 60° C. 58° D. 50°
3 如图,已知图中有两对三角形全等.
(1) △ABM≌________,在这两个全等三角形中,AB的对应边是________,BM的对应边是________,MA的对应边是________;
(2) △ABN≌________,在这两个全等三角形中,∠BAN的对应角是________,∠B的对应角是________,∠ANB的对应角是________.
4 (2025泰州海陵期末)如图,点E,F分别在线段AC,AB上,若△ABE≌△ACF,且AB=10,AE=4,则EC的长为________.
5 (2025盐城月考)如图,点A,B,C,D在同一直线上,△ACE≌△DBF,AD=8,BC=2.
(1) 求AC的长;
(2) 求证:AE∥DF.
6 (2024苏州工业园区期末)如图所示的三角形是由若干个全等的小等边三角形组成的.
(1) 在图1中,把该三角形分割成2个全等的三角形;
(2) 在图2中,把该三角形分割成3个全等的三角形;
(3) 在图3中,把该三角形分割成4个全等的三角形.
图1 图2 图3
建议用时:20+5分钟
7 如图,已知△ABC≌△DEC,∠ACB=100°,∠D=35°,则∠E的度数为( )
A. 35° B. 45° C. 55° D. 无法计算
(第7题) (第8题) (第9题) (第10题)
8 如图,点E在AB上,AC与DE相交于点F,△ABC≌△DEC,∠A=20°,∠B=∠CEB=65°,则∠DFA的度数为( )
A. 65° B. 70° C. 85° D. 110°
9 如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE相交于点F,△ADC≌△BDF,若BD=4,DC=2,则△ABC的面积为________.
10 (2025宜兴月考)如图,△AOB≌△ADC,∠O=90°,若∠OAD=α,∠ABO=β.当BC∥OA时,α与β之间的数量关系为________.
11 如图,A,E,C三点在同一直线上,且△ABC≌△DAE.
(1) 线段DE,CE,BC有怎样的数量关系?请说明理由;
(2) 请你猜想△ADE满足什么条件时,DE∥BC,并说明理由.
12 (2025广陵月考)如图,在△ABC中,AB=AC=24 cm,BC=16 cm,D为AB的中点.如果点P在线段BC上以4 cm/s的速度由点B向点C运动.同时,点Q在线段CA上以a cm/s的速度由点C向A点运动,设运动的时间为t s.
(1) ①BP=________cm;②CP=________cm;③CQ=________cm;(用含t,a的式子表示)
(2) 若以D,B,P为顶点的三角形和以P,C,Q为顶点的三角形全等,求a,t的值.
1.2 全等三角形
1. A 2. D 3. (1) △ACN AC CN NA
(2) △ACM ∠CAM ∠C ∠AMC 4. 6
5. (1) 解:因为△ACE≌△DBF,
所以AC=DB.
因为AC+BD=AD+BC,
所以2AC=AD+BC.
因为AD=8,BC=2,
所以2AC=8+2=10,
所以AC=5.
(2) 证明:因为△ACE≌△DBF,
所以∠A=∠D,
所以AE∥DF.
6. 解:(1) 如图1,作高,图1即为所求.
(2) 如图2,作角平分线,图2即为所求.
(3) 如图3,连接各边中点,图3即为所求.
图1 图2 图3
7. B 8. B 9. 12 10. α=2β
11. 解: (1) DE=CE+BC.理由如下:
因为△ABC≌△DAE,
所以AE=BC,DE=AC.
因为A,E,C三点在同一直线上,
所以AC=AE+CE,
所以DE=CE+BC.
(2) 当△ADE满足∠AED=90°时,DE∥BC.理由如下:
因为△ABC≌△DAE,∠AED=90°,
所以∠C=∠AED=90°,∠DEC=180°-∠AED=90°,
所以∠C=∠DEC,
所以DE∥BC,
即当△ADE满足∠AED=90°时,DE∥BC.
12. 解:(1) 4t 16-4t at
(2) 因为BP=4t cm,BD=12 cm,CP=(16-4t) cm,CQ=at cm,
所以∠B=∠C,
可分为两种情况,
①若△DBP≌△QCP,
则
所以
所以
②若△DBP≌△PCQ,
则
所以
所以
综上,a的值为6,t的值为2或a的值为4,t的值为1.
同课章节目录
