1.5 等腰三角形 同步练(含答案) 2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 1.5 等腰三角形 同步练(含答案) 2025-2026学年数学苏科版(2024)八年级上册 | 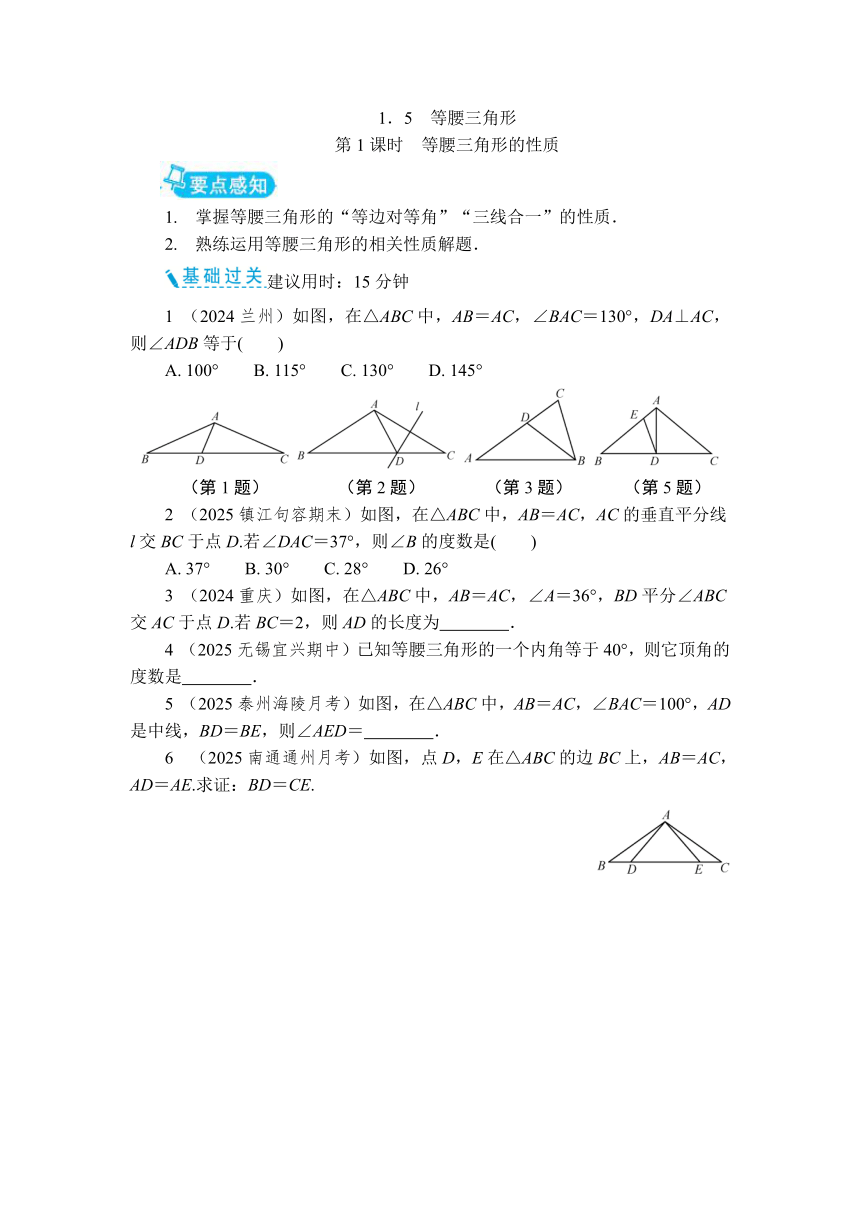 | |
| 格式 | docx | ||
| 文件大小 | 552.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 15:24:14 | ||
图片预览



文档简介
1.5 等腰三角形
第1课时 等腰三角形的性质
1. 掌握等腰三角形的“等边对等角”“三线合一”的性质.
2. 熟练运用等腰三角形的相关性质解题.
建议用时:15分钟
1 (2024兰州)如图,在△ABC中,AB=AC,∠BAC=130°,DA⊥AC,则∠ADB等于( )
A. 100° B. 115° C. 130° D. 145°
(第1题) (第2题) (第3题) (第5题)
2 (2025镇江句容期末)如图,在△ABC中,AB=AC,AC的垂直平分线l交BC于点D.若∠DAC=37°,则∠B的度数是( )
A. 37° B. 30° C. 28° D. 26°
3 (2024重庆)如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D.若BC=2,则AD的长度为 .
4 (2025无锡宜兴期中)已知等腰三角形的一个内角等于40°,则它顶角的度数是 .
5 (2025泰州海陵月考)如图,在△ABC中,AB=AC,∠BAC=100°,AD是中线,BD=BE,则∠AED= .
6 (2025南通通州月考)如图,点D,E在△ABC的边BC上,AB=AC,AD=AE.求证:BD=CE.
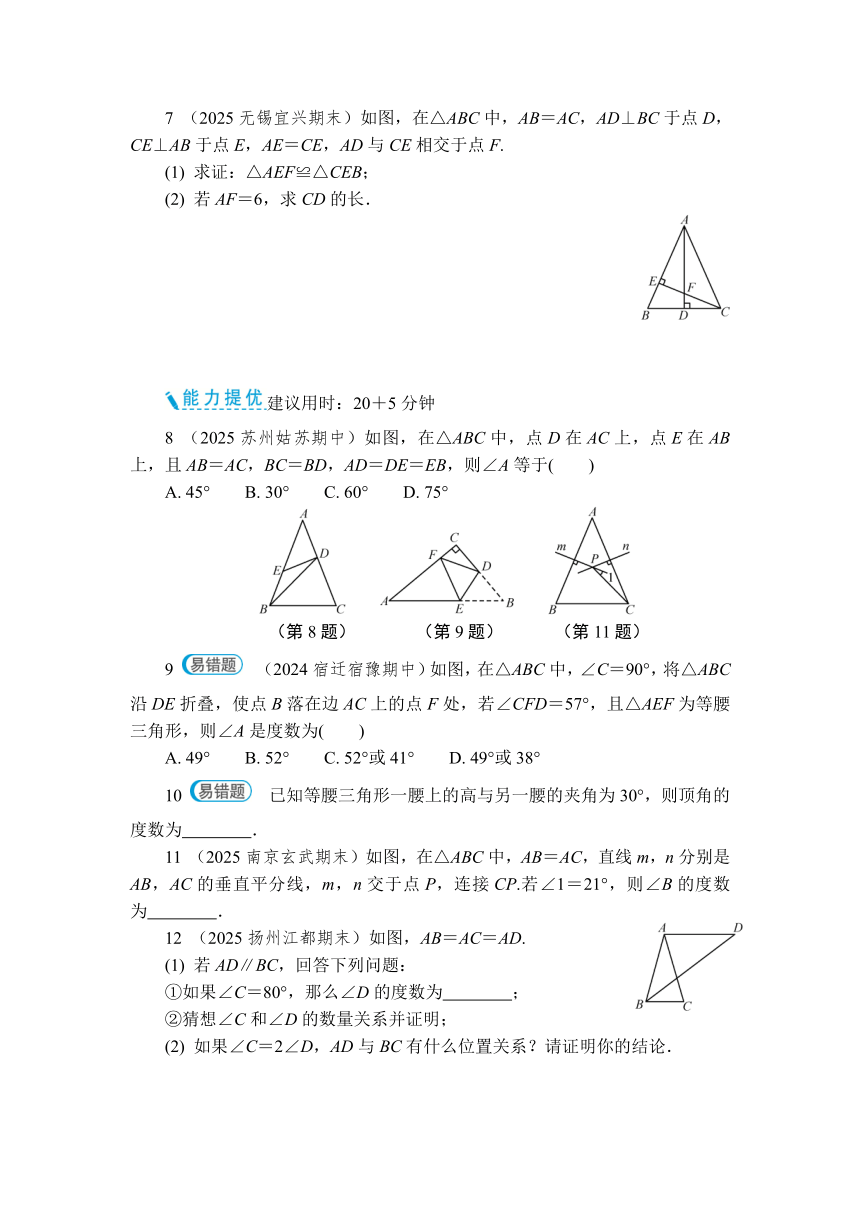
7 (2025无锡宜兴期末)如图,在△ABC中,AB=AC,AD⊥BC于点D,CE⊥AB于点E,AE=CE,AD与CE相交于点F.
(1) 求证:△AEF≌△CEB;
(2) 若AF=6,求CD的长.
建议用时:20+5分钟
8 (2025苏州姑苏期中)如图,在△ABC中,点D在AC上,点E在AB上,且AB=AC,BC=BD,AD=DE=EB,则∠A等于( )
A. 45° B. 30° C. 60° D. 75°
(第8题) (第9题) (第11题)
9 (2024宿迁宿豫期中)如图,在△ABC中,∠C=90°,将△ABC沿DE折叠,使点B落在边AC上的点F处,若∠CFD=57°,且△AEF为等腰三角形,则∠A是度数为( )
A. 49° B. 52° C. 52°或41° D. 49°或38°
10 已知等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为 .
11 (2025南京玄武期末)如图,在△ABC中,AB=AC,直线m,n分别是AB,AC的垂直平分线,m,n交于点P,连接CP.若∠1=21°,则∠B的度数为 .
12 (2025扬州江都期末)如图,AB=AC=AD.
(1) 若AD∥BC,回答下列问题:
①如果∠C=80°,那么∠D的度数为 ;
②猜想∠C和∠D的数量关系并证明;
(2) 如果∠C=2∠D,AD与BC有什么位置关系?请证明你的结论.
13 如图1,图2,在四边形ABCD中,∠BAD=α,∠BCD=180°-α,BD平分∠ABC.
(1) 如图1,若α=90°,根据教材中一个重要性质直接可得DA=CD,这个性质是 ;
(2) 问题解决:如图2,求证AD=CD;
(3) 问题拓展:如图3,在等腰三角形ABC中,∠BAC=100°,BD平分∠ABC,求证:BD+AD=BC.
图1 图2 图3
第2课时 等腰三角形的判定
掌握等腰三角形的判定定理(等角对等边).
建议用时:15分钟
1 下列选项中能判定三角形是等腰三角形的是( )
A. 有两个角为30°,60° B. 有两个角为40°,80°
C. 有两个角为50°,80° D. 有两个角为100°,120°
2 (教材P45练习2变式)如图,把一张对边平行的纸条折叠,则重合部分是( )
A. 等边三角形 B. 等腰三角形 C. 直角三角形 D. 无法确定
(第2题) (第3题) (第4题) (第5题)
3 (教材P45练习1变式)如图,在△ABC中,AB=AC,∠ABC=36°,D,E是BC上的点,∠BAD=∠DAE=∠EAC,则图中等腰三角形的个数是( )
A. 2 B. 3 C. 4 D. 6
4 如图,在△ABC中,BD平分∠ABC交AC于点D,DE∥AB交BC于点E,BE=2,则DE的长是 .
5 如图,在△ABC中,∠ABC的平分线交AC于点D,AD=6,过点D作DE∥BC交AB于点E,若△AED的周长为16,则边AB的长为 .
6 (2025盐城期末)如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,BF平分∠ABC交CD于点E,交AC于点F.求证:CE=CF.
7 (2025扬州邗江月考)如图,已知D,E分别是△ABC的边BA和BC延长线上的点,作∠DAC的平分线AF,若AF∥BC.
(1) 求证:△ABC是等腰三角形;
(2) 作∠ACE的平分线交AF于点G,若∠B=40°,求∠AGC的度数.
建议用时:20+5分钟
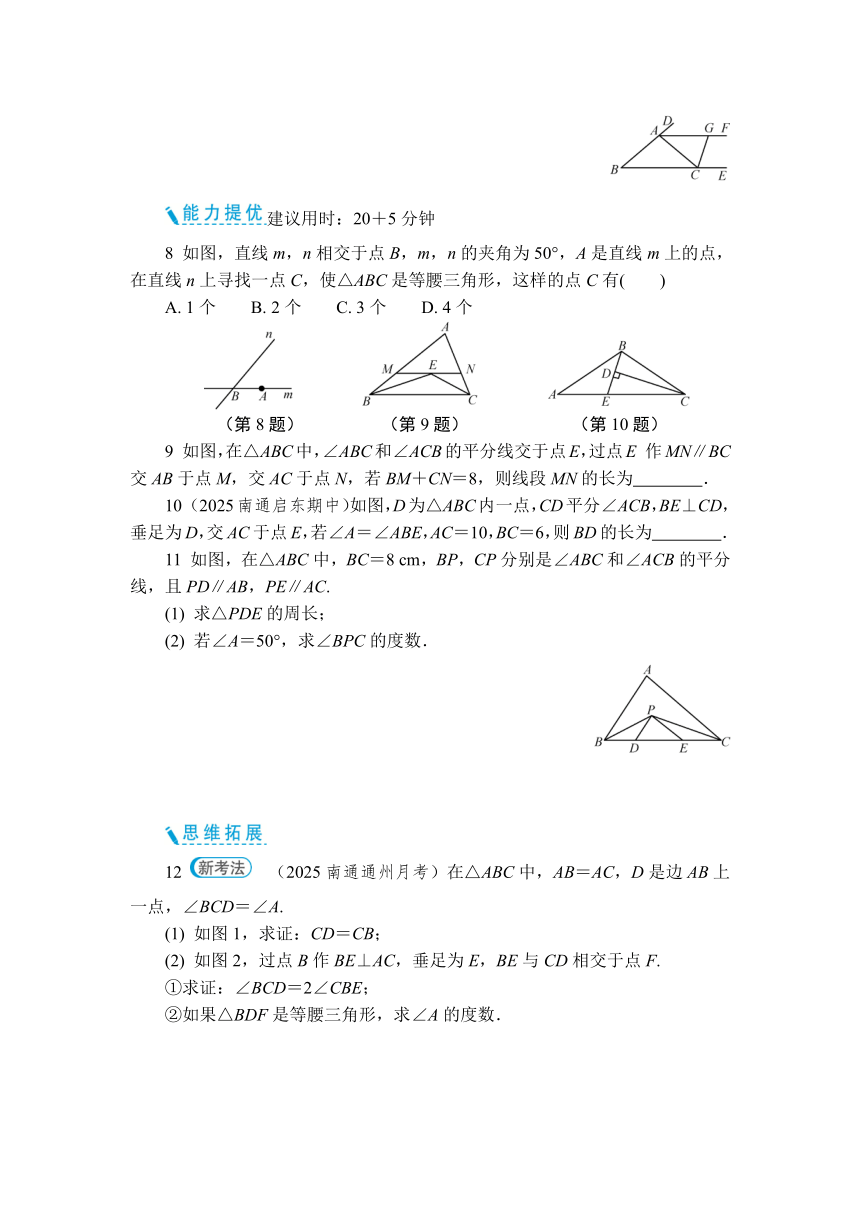
8 如图,直线m,n相交于点B,m,n的夹角为50°,A是直线m上的点,在直线n上寻找一点C,使△ABC是等腰三角形,这样的点C有( )
A. 1个 B. 2个 C. 3个 D. 4个
(第8题) (第9题) (第10题)
9 如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E 作MN∥BC交AB于点M,交AC于点N,若BM+CN=8,则线段MN的长为 .
10 (2025南通启东期中)如图,D为△ABC内一点,CD平分∠ACB,BE⊥CD,垂足为D,交AC于点E,若∠A=∠ABE,AC=10,BC=6,则BD的长为 .
11 如图,在△ABC中,BC=8 cm,BP,CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC.
(1) 求△PDE的周长;
(2) 若∠A=50°,求∠BPC的度数.
12 (2025南通通州月考)在△ABC中,AB=AC,D是边AB上一点,∠BCD=∠A.
(1) 如图1,求证:CD=CB;
(2) 如图2,过点B作BE⊥AC,垂足为E,BE与CD相交于点F.
①求证:∠BCD=2∠CBE;
②如果△BDF是等腰三角形,求∠A的度数.
图1 图2 备用图
第3课时 等边三角形的判定与性质
1. 掌握等边三角形的判定方法.
2. 掌握在直角三角形中,30°角所对的边是斜边的一半,并能利用该性质进行证明、计算.
建议用时:15分钟
1 (教材P47练习1变式)如图,BD,CE是等边三角形ABC的中线,则∠1的度数为( )
A. 30° B. 45° C. 60° D. 无法确定
(第1题) (第2题) (第3题) (第4题) (第5题)
2 (2025南通海门月考)如图,若△ABC是等边三角形,AB=6,BD是∠ABC的平分线,延长BC到点E,使CE=CD,则BE的长为( )
A. 7 B. 8 C. 9 D. 10
3 如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,若BD=2,则AB的长为 .
4 如图,在等边三角形ABC中,P为BC上一点,且∠1=∠2,则∠3的度数为 .
5 (2025苏州太仓期末)如图,l1∥l2,等边三角形ABC的顶点A在直线l1上,l2与△ABC的两边AC,BC分别相交.若∠1=138°,则∠2的度数为 .
6 如图,△ABC为等边三角形,M是线段BC上的任意一点,N是线段CA上任意一点,且BM=CN,直线BN与AM相交于点Q.
(1) 求证:△BAN≌△ACM;
(2) 求∠BQM的度数.
7 如图,在△ABC中,AB=AC,∠BAC=120°,点D,E在BC上,且AE=BE.
(1) 求∠CAE的度数;
(2) 若D为线段EC的中点,求证:△ADE是等边三角形.
建议用时:20+5分钟
8 (2025南通如皋期中)如图,在△ABC中,AB=AC=12,∠BAC=120°,D是边BC上的任意一点,则AD的长不可能是( )
A. 5 B. 6 C. 7 D. 8
(第8题) (第9题) (第10题) (第11题)
9 (2025宿迁泗洪期中)如图,在边长为2的等边三角形ABC中,点D在边BC上运动(不与点B,C重合),点E在边AB的延长线上,点F在边AC的延长线上,AD=DE=DF,点D在边BC上从点B至点C的运动过程中,△BED周长变化规律为( )
A. 不变 B. 一直变小 C. 先变大后变小 D. 先变小后变大
10 如图,△ABC是等边三角形,D是边BC上任意一点,DE⊥AB于点E,DF⊥AC于点F.若BC=4,则BE+CF= .
11 如图,∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为 .
12 如图,点A,B,C在同一直线上,△ABD,△BCE都是等边三角形.
(1) 求证:AE=CD;
(2) 若M,N分别是AE,CD的中点,试判断△BMN的形状,并证明你的结论.
13 在等边三角形ABC中,点E在边AB上,点D在CB的延长线上,且DE=EC.
(1) 如图1,当E为AB的中点时,求证:CB=2BD;
(2) 如图2,若AB=12,AE=2,求CD的长.
图1 图2
第4课时 直角三角形的性质
1. 熟练运用直角三角形斜边上的中线的性质解题.
2. 掌握等腰三角形的判定与性质的综合应用.
建议用时:15分钟
1 (2025盐城期中)如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AB的长为4.8 km,则M,C两点间的距离为( )
A. 2.4 km B. 3.6 km C. 4.2 km D. 4.8 km
(第1题) (第2题) (第4题) (第5题)
2 (教材P48例4变式)如图,在Rt△ABC中,CD是斜边AB上的中线,若∠A=20°,则∠BDC的度数为( )
A. 30° B. 40° C. 45° D. 60°
3 (2025南京建邺期末)若直角三角形斜边上的中线与高的长分别是5和4,则这个三角形的面积是 .
4 (2024徐州铜山期中)如图,在△ABC中,AB=AC=8,AD是角平分线,BE是中线,则DE的长为 .
5 如图,AD是△ABC的中线,DE是△ADC的高,AB=16,AC=22,DE=8,则点D到AB的距离是 .
6 如图,∠ABC=∠ADC=90°,E,F分别是AC,BD的中点,求证:EF⊥BD.
7 (2024东台期末)如图,在△ABC中,CE,BD分别是边AB,AC上的高,M是BC的中点,连接DE,EM,MD.
(1) 求证:ME=MD;
(2) 若∠A=45°,求∠EDM的度数.
建议用时:20+5分钟
8 (2025苏州期末)如图,在△ABC中,∠ACB=90°,D是边AB的中点,以点C为圆心,CD的长为半径画弧,与线段BD相交于另一点E,连接CE.若∠A=∠DCE,则∠A的度数为( )
A. 20° B. 30° C. 36° D. 40°
(第8题) (第9题) (第10题) (第11题)
9 如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,BD.若∠EBD=35°,则∠BAD的度数为( )
A. 55° B. 58° C. 65° D. 68°
10 (2024盐城建湖期末)如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠BAD=45°,连接AC,BD,M是AC的中点,连接BM,DM.若△BMD的面积为32,则AC的长为 .
11 如图,在Rt△ABC中,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A的度数为 .
12 如图,在△ABC中,AD是高,CE是中线,G是CE的中点,DG⊥CE,垂足为G.
(1) 求证:DC=BE;
(2) 若∠AEC=75°,求∠BCE的度数.
13 (2025苏州期末)已知线段AC,以AC为斜边作Rt△ABC和Rt△ADC,连接BD,M,N分别是线段AC,BD的中点,连接MN,MB.
(1) 如图1,Rt△ABC和Rt△ADC在线段AC的两侧.
①求证:MN⊥BD;
②若∠BAC=45°,∠DAC=28°,请求出∠BMN的度数;
(2) 如图2,Rt△ABC和Rt△ADC在线段AC的同侧,若∠BAC=α,∠DAC=β(α>β),则∠BMN的度数为 (用含α,β的代数式表示).
图1 图2
1.5 等腰三角形
第1课时 等腰三角形的性质
1. B 2. A 3. 2 4. 40°或100° 5. 110°
6. 证明:过点A作AF⊥BC,垂足为F,
因为AB=AC,AF⊥BC,
所以BF=CF.
因为AD=AE,AF⊥DE,
所以DF=EF,
所以BF-DF=CF-EF,
所以BD=CE.
7. (1)证明:因为AD⊥BC,
所以∠B+∠BAD=90°.
因为CE⊥AB,
所以∠B+∠BCE=90°,
所以∠EAF=∠ECB.
在△AEF和△CEB中,
所以△AEF≌△CEB(ASA).
(2) 解:因为△AEF≌△CEB,
所以AF=BC.
因为AB=AC,AD⊥BC,
所以CD=BD,BC=2CD,
所以AF=2CD,
所以CD=AF=×6=3.
8. A 9. D 10. 60°或120° 11. 67°
12. 解:(1) ①40°
②∠C=2∠D,理由如下:
因为AD∥BC,
所以∠D=∠DBC,
又因为AB=AD,
所以∠D=∠ABD,
所以∠ABC=2∠D.
因为AB=AC,
所以∠C=∠ABC=2∠D.
(2) AD∥BC,证明如下:
因为AB=AC,∠C=2∠D,
所以∠ABC=∠C=2∠D.
因为AB=AD,
所以∠ABD=∠D,
所以∠DBC=∠D,
所以AD∥BC.
13. (1) 角平分线上的点到角的两边距离相等
(2) 证明:如图1,作DE⊥BA交BA的延长线于点E,DF⊥BC于点F.
因为BD平分∠EBF,DE⊥BE,DF⊥BF,
所以DE=DF.
因为∠BAD+∠C=180°,∠BAD+∠EAD=180°,
所以∠EAD=∠C.
在△DEA和△DFC中,
所以△DEA≌△DFC(AAS),
所以DA=DC.
(3) 证明:如图2,在BC上截取BK=BD,连接DK.
因为AB=AC,∠A=100°,
所以∠ABC=∠C=40°.
因为BD平分∠ABC,
所以∠DBK=∠ABC=20°.
因为BD=BK,
所以∠BKD=∠BDK=80°,即∠A+∠BKD=180°,
由(2)的结论得AD=DK,
因为∠BKD=∠C+∠KDC,
所以∠KDC=∠C=40°,
所以DK=CK,
所以AD=DK=CK,
所以BD+AD=BK+CK=BC.
图1 图2
第2课时 等腰三角形的判定
1. C 2. B 3. D 4. 2 5. 10
6. 证明:因为∠ACB=90°,CD⊥AB,
所以∠CBF+∠CFB=∠DBE+∠DEB=90°.
因为BF平分∠ABC,
所以∠CBF=∠DBE,
所以∠CFB=∠DEB.
又因为∠FEC=∠DEB,
所以∠CFB=∠FEC,
所以CE=CF.
7. (1) 证明:因为AF平分∠DAC,
所以∠DAF=∠CAF.
因为AF∥BC,
所以∠DAF=∠B,∠CAF=∠ACB,
所以∠B=∠ACB,
所以AB=AC,即△ABC是等腰三角形.
(2) 解:因为AB=AC,∠B=40°,
所以∠ACB=∠B=40°,
所以∠ACE=180°-∠ACB=140°.
因为CG平分∠ACE,
所以∠ACG=∠GCE=∠ACE=70°.
因为AF∥BC,
所以∠AGC=∠GCE=70°.
8. D 9. 8 10. 2
11. 解:(1) 因为BP,CP分别是∠ABC和∠ACB的平分线,
所以∠ABP=∠PBD,∠ACP=∠PCE.
因为PD∥AB,PE∥AC,
所以∠ABP=∠BPD,∠ACP=∠CPE,
所以∠PBD=∠BPD,∠PCE=∠CPE,
所以BD=PD,CE=PE,
所以△PDE的周长=PD+DE+PE=BD+DE+EC=BC=8 cm.
(2) 因为∠A=50°,
所以∠ABC+∠ACB=130°,
所以∠ABC+∠ACB=65°.
因为BP,CP分别是∠ABC和∠ACB的平分线,
所以∠PBC=∠ABC,∠PCB=∠ACB,
所以∠PBC+∠PCB=65°,
所以∠BPC=180°-65°=115°.
12. (1) 证明:因为AB=AC,
所以∠ABC=∠ACB.
因为∠BDC是△ADC的一个外角,
所以∠BDC=∠A+∠ACD.
因为∠ACB=∠BCD+∠ACD,∠BCD=∠A,
所以∠BDC=∠ACB,
所以∠ABC=∠BDC.
所以CD=CB.
(2) ①证明:因为BE⊥AC,
所以∠BEC=90°,
所以∠CBE+∠ACB=90°.
设∠CBE=α,则∠ACB=90°-α,
所以∠ACB=∠ABC=∠BDC=90°-α,
所以∠BCD=180°-∠BDC-∠ABC=180°-(90°-α)-(90°-α)=2α,
所以∠BCD=2∠CBE.
②解:因为∠BFD是△CBF的一个外角,
所以∠BFD=∠CBE+∠BCD=α+2α=3α.
当BD=BF时,∠BDC=∠BFD=3α,
因为∠ACB=∠ABC=∠BDC=90°-α,
所以90°-α=3α,
所以α=22.5°,
所以∠A=∠BCD=2α=45°;
当DB=DF时,∠DBE=∠BFD=3α,
因为∠DBE=∠ABC-∠CBE=90°-α-α=90°-2α,
所以90°-2α=3α,
所以α=18°,
所以∠A=∠BCD=2α=36°;
当FB=FD时,∠DBE=∠BDF,
因为∠BDF=∠ABC>∠DBF,
所以不存在FB=FD.
综上,∠A的度数为45°或36°.
第3课时 等边三角形的判定与性质
1. C 2. C 3. 8 4. 60° 5. 102°
6. (1) 证明:因为△ABC为等边三角形,
所以AB=BC=CA,∠BAC=∠BCA=60°.
因为BM=CN,
所以CM=AN.
在△BAN和△ACM中,
所以△BAN≌△ACM(SAS).
(2) 解:因为△BAN≌△ACM,
所以∠CAM=∠ABN,
所以∠BQM=∠ABN+∠BAQ=∠CAM+∠BAQ=∠BAC=60°.
7. (1) 解:因为AB=AC,∠BAC=120°,
所以∠B=∠C=30°.
因为AE=BE,所以∠B=∠EAB=30°.
因为∠BAC=120°,所以∠CAE=∠BAC-∠EAB=90°,
即∠CAE=90°.
(2) 证明:由(1),得∠CAE=90°,∠C=30°,
所以∠AED=60°,所以AE=EC.
因为D为线段EC的中点,
所以ED=EC,
所以AE=ED,则△ADE是等边三角形.
8. A 9. D 10. 2 11. 2n-1
12. (1) 证明:因为△ABD,△BCE都是等边三角形,
所以AB=BD,BC=BE,∠ABD=∠CBE=60°,
所以∠ABD+∠DBE=∠DBE+∠CBE,即∠ABE=∠DBC.
在△ABE和△DBC中,
所以△ABE≌△DBC(SAS),
所以AE=CD.
(2) 解:△BMN是等边三角形,理由如下:
因为△ABE≌△DBC,
所以∠BAE=∠BDC.
因为AE=CD,M,N分别是AE,CD的中点,
所以AM=AE=CD=DN.
在△ABM和△DBN中,
所以△ABM≌△DBN(SAS),
所以BM=BN,∠ABM=∠DBN,
所以∠DBM+∠DBN=∠DBM+∠ABM=∠ABD=60°,
即∠MBN=60°,
所以△BMN是等边三角形.
13. (1) 证明:因为△ABC为等边三角形,
所以∠ABC=∠A=∠ACB=60°.
因为E为AB的中点,
所以CE⊥AB,CE是∠ACB的平分线,
所以∠BEC=90°,∠BCE=30°,
所以2EB=BC.
因为ED=EC,
所以∠EDC=∠ECD=30°,
所以∠DEB=∠ABC-∠EDC=60°-30°=30°,
所以BD=BE,
所以2BD=BC.
(2) 解:如图,过点E作EF∥BC,交AC于点F.
因为△ABC为等边三角形,
所以∠A=∠AFE=∠ACB=∠ABC=60°,
所以△AEF为等边三角形,
所以∠EFC=∠EBD=120°,EF=AE.
因为ED=EC,
所以∠EDB=∠ECB,∠ECB=∠FEC,
所以∠EDB=∠FEC.
在△BDE和△FEC中,
所以△BDE≌△FEC(AAS),
所以BD=EF,
所以AE=BD=2,
所以CD=BC+BD=12+2=14.
第4课时 直角三角形的性质
1. A 2. B 3. 20 4. 4 5. 11
6. 证明:连接DE,BE.
因为∠ABC=∠ADC=90°,E为AC的中点,
所以BE=AC,DE=AC,所以BE=DE.
因为F为BD的中点,所以EF⊥BD.
7. (1) 证明:因为CE,BD分别是边AB,AC上的高,
所以∠BEC=∠CDB=90°.
因为M是BC的中点,
所以EM=BC,DM=BC,所以ME=MD.
(2) 解:因为∠A=45°,
所以∠ABC+∠ACB=180°-∠A=135°.
因为∠BEC=∠CDB=90°,M为BC的中点,
所以EM=BM,DM=CM,
所以∠BEM=∠ABC,∠MDC=∠ACB,
所以∠ABC+∠BEM+∠ACB+∠MDC=135°×2=270°,
所以∠EMB+∠DMC=180°×2-270°=90°,
所以∠EMD=180°-(∠EMB+∠DMC)=180°-90°=90°.
因为ME=MD,所以∠EDM=45°.
8. C 9. A 10. 16 11. 30°
12. (1) 证明:连接ED.因为G是CE的中点,DG⊥CE,
所以DE=DC.
因为AD是高,所以△ABD是直角三角形.
又因为CE是中线,所以E是AB的中点,
所以ED是Rt△ABD的中线,
所以DE=BE=AE,所以BE=CD.
(2) 解:因为DE=BE=AE=DC,
所以∠BCE=∠DEC,∠BAD=∠ADE,
所以∠EDB=2∠BCE,
∠ADE=
==.
因为AD是高,所以∠EDB+∠ADE=90°,
即2∠BCE+=90°,
所以3∠BCE=75°,所以∠BCE=25°.
13. (1) ①证明:如图1,连接MD.
因为∠ABC=∠ADC=90°,M是AC的中点,
所以BM=AC,DM=AC,
所以BM=DM.
又因为N是BD的中点,
所以MN⊥BD.
②解:因为∠ABC=∠ADC=90°,M是AC的中点,
所以BM=AM=MC=DM.
又因为∠BAC=45°,∠DAC=28°,
所以∠MBC=∠MCB=90°-∠BAC=45°,∠MCD=∠CDM=90°-∠DAC=62°,
所以∠BMD=360°-45°×2-62°×2=146°.
因为BM=DM,MN⊥BD,
所以∠BMN=∠DMN=∠BMD=×146°=73°.
(2) α-β 提示:如图2,连接MD,因为∠ABC=∠ADC=90°,M是AC的中点,所以AM=BM=MD,所以∠MBA=∠BAC=α,∠MDA=∠DAC=β,所以∠AMB=180°-2α,∠CMD=2β,所以∠BMD=180°-∠AMB-∠CMD=2α-2β.因为BM=MD,N是BD的中点,所以∠BMN=∠DMN=∠BMD=(2α-2β)=α-β.
图1 图2
第1课时 等腰三角形的性质
1. 掌握等腰三角形的“等边对等角”“三线合一”的性质.
2. 熟练运用等腰三角形的相关性质解题.
建议用时:15分钟
1 (2024兰州)如图,在△ABC中,AB=AC,∠BAC=130°,DA⊥AC,则∠ADB等于( )
A. 100° B. 115° C. 130° D. 145°
(第1题) (第2题) (第3题) (第5题)
2 (2025镇江句容期末)如图,在△ABC中,AB=AC,AC的垂直平分线l交BC于点D.若∠DAC=37°,则∠B的度数是( )
A. 37° B. 30° C. 28° D. 26°
3 (2024重庆)如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D.若BC=2,则AD的长度为 .
4 (2025无锡宜兴期中)已知等腰三角形的一个内角等于40°,则它顶角的度数是 .
5 (2025泰州海陵月考)如图,在△ABC中,AB=AC,∠BAC=100°,AD是中线,BD=BE,则∠AED= .
6 (2025南通通州月考)如图,点D,E在△ABC的边BC上,AB=AC,AD=AE.求证:BD=CE.
7 (2025无锡宜兴期末)如图,在△ABC中,AB=AC,AD⊥BC于点D,CE⊥AB于点E,AE=CE,AD与CE相交于点F.
(1) 求证:△AEF≌△CEB;
(2) 若AF=6,求CD的长.
建议用时:20+5分钟
8 (2025苏州姑苏期中)如图,在△ABC中,点D在AC上,点E在AB上,且AB=AC,BC=BD,AD=DE=EB,则∠A等于( )
A. 45° B. 30° C. 60° D. 75°
(第8题) (第9题) (第11题)
9 (2024宿迁宿豫期中)如图,在△ABC中,∠C=90°,将△ABC沿DE折叠,使点B落在边AC上的点F处,若∠CFD=57°,且△AEF为等腰三角形,则∠A是度数为( )
A. 49° B. 52° C. 52°或41° D. 49°或38°
10 已知等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为 .
11 (2025南京玄武期末)如图,在△ABC中,AB=AC,直线m,n分别是AB,AC的垂直平分线,m,n交于点P,连接CP.若∠1=21°,则∠B的度数为 .
12 (2025扬州江都期末)如图,AB=AC=AD.
(1) 若AD∥BC,回答下列问题:
①如果∠C=80°,那么∠D的度数为 ;
②猜想∠C和∠D的数量关系并证明;
(2) 如果∠C=2∠D,AD与BC有什么位置关系?请证明你的结论.
13 如图1,图2,在四边形ABCD中,∠BAD=α,∠BCD=180°-α,BD平分∠ABC.
(1) 如图1,若α=90°,根据教材中一个重要性质直接可得DA=CD,这个性质是 ;
(2) 问题解决:如图2,求证AD=CD;
(3) 问题拓展:如图3,在等腰三角形ABC中,∠BAC=100°,BD平分∠ABC,求证:BD+AD=BC.
图1 图2 图3
第2课时 等腰三角形的判定
掌握等腰三角形的判定定理(等角对等边).
建议用时:15分钟
1 下列选项中能判定三角形是等腰三角形的是( )
A. 有两个角为30°,60° B. 有两个角为40°,80°
C. 有两个角为50°,80° D. 有两个角为100°,120°
2 (教材P45练习2变式)如图,把一张对边平行的纸条折叠,则重合部分是( )
A. 等边三角形 B. 等腰三角形 C. 直角三角形 D. 无法确定
(第2题) (第3题) (第4题) (第5题)
3 (教材P45练习1变式)如图,在△ABC中,AB=AC,∠ABC=36°,D,E是BC上的点,∠BAD=∠DAE=∠EAC,则图中等腰三角形的个数是( )
A. 2 B. 3 C. 4 D. 6
4 如图,在△ABC中,BD平分∠ABC交AC于点D,DE∥AB交BC于点E,BE=2,则DE的长是 .
5 如图,在△ABC中,∠ABC的平分线交AC于点D,AD=6,过点D作DE∥BC交AB于点E,若△AED的周长为16,则边AB的长为 .
6 (2025盐城期末)如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,BF平分∠ABC交CD于点E,交AC于点F.求证:CE=CF.
7 (2025扬州邗江月考)如图,已知D,E分别是△ABC的边BA和BC延长线上的点,作∠DAC的平分线AF,若AF∥BC.
(1) 求证:△ABC是等腰三角形;
(2) 作∠ACE的平分线交AF于点G,若∠B=40°,求∠AGC的度数.
建议用时:20+5分钟
8 如图,直线m,n相交于点B,m,n的夹角为50°,A是直线m上的点,在直线n上寻找一点C,使△ABC是等腰三角形,这样的点C有( )
A. 1个 B. 2个 C. 3个 D. 4个
(第8题) (第9题) (第10题)
9 如图,在△ABC中,∠ABC和∠ACB的平分线交于点E,过点E 作MN∥BC交AB于点M,交AC于点N,若BM+CN=8,则线段MN的长为 .
10 (2025南通启东期中)如图,D为△ABC内一点,CD平分∠ACB,BE⊥CD,垂足为D,交AC于点E,若∠A=∠ABE,AC=10,BC=6,则BD的长为 .
11 如图,在△ABC中,BC=8 cm,BP,CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC.
(1) 求△PDE的周长;
(2) 若∠A=50°,求∠BPC的度数.
12 (2025南通通州月考)在△ABC中,AB=AC,D是边AB上一点,∠BCD=∠A.
(1) 如图1,求证:CD=CB;
(2) 如图2,过点B作BE⊥AC,垂足为E,BE与CD相交于点F.
①求证:∠BCD=2∠CBE;
②如果△BDF是等腰三角形,求∠A的度数.
图1 图2 备用图
第3课时 等边三角形的判定与性质
1. 掌握等边三角形的判定方法.
2. 掌握在直角三角形中,30°角所对的边是斜边的一半,并能利用该性质进行证明、计算.
建议用时:15分钟
1 (教材P47练习1变式)如图,BD,CE是等边三角形ABC的中线,则∠1的度数为( )
A. 30° B. 45° C. 60° D. 无法确定
(第1题) (第2题) (第3题) (第4题) (第5题)
2 (2025南通海门月考)如图,若△ABC是等边三角形,AB=6,BD是∠ABC的平分线,延长BC到点E,使CE=CD,则BE的长为( )
A. 7 B. 8 C. 9 D. 10
3 如图,在△ABC中,∠ACB=90°,CD是高,∠A=30°,若BD=2,则AB的长为 .
4 如图,在等边三角形ABC中,P为BC上一点,且∠1=∠2,则∠3的度数为 .
5 (2025苏州太仓期末)如图,l1∥l2,等边三角形ABC的顶点A在直线l1上,l2与△ABC的两边AC,BC分别相交.若∠1=138°,则∠2的度数为 .
6 如图,△ABC为等边三角形,M是线段BC上的任意一点,N是线段CA上任意一点,且BM=CN,直线BN与AM相交于点Q.
(1) 求证:△BAN≌△ACM;
(2) 求∠BQM的度数.
7 如图,在△ABC中,AB=AC,∠BAC=120°,点D,E在BC上,且AE=BE.
(1) 求∠CAE的度数;
(2) 若D为线段EC的中点,求证:△ADE是等边三角形.
建议用时:20+5分钟
8 (2025南通如皋期中)如图,在△ABC中,AB=AC=12,∠BAC=120°,D是边BC上的任意一点,则AD的长不可能是( )
A. 5 B. 6 C. 7 D. 8
(第8题) (第9题) (第10题) (第11题)
9 (2025宿迁泗洪期中)如图,在边长为2的等边三角形ABC中,点D在边BC上运动(不与点B,C重合),点E在边AB的延长线上,点F在边AC的延长线上,AD=DE=DF,点D在边BC上从点B至点C的运动过程中,△BED周长变化规律为( )
A. 不变 B. 一直变小 C. 先变大后变小 D. 先变小后变大
10 如图,△ABC是等边三角形,D是边BC上任意一点,DE⊥AB于点E,DF⊥AC于点F.若BC=4,则BE+CF= .
11 如图,∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为 .
12 如图,点A,B,C在同一直线上,△ABD,△BCE都是等边三角形.
(1) 求证:AE=CD;
(2) 若M,N分别是AE,CD的中点,试判断△BMN的形状,并证明你的结论.
13 在等边三角形ABC中,点E在边AB上,点D在CB的延长线上,且DE=EC.
(1) 如图1,当E为AB的中点时,求证:CB=2BD;
(2) 如图2,若AB=12,AE=2,求CD的长.
图1 图2
第4课时 直角三角形的性质
1. 熟练运用直角三角形斜边上的中线的性质解题.
2. 掌握等腰三角形的判定与性质的综合应用.
建议用时:15分钟
1 (2025盐城期中)如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AB的长为4.8 km,则M,C两点间的距离为( )
A. 2.4 km B. 3.6 km C. 4.2 km D. 4.8 km
(第1题) (第2题) (第4题) (第5题)
2 (教材P48例4变式)如图,在Rt△ABC中,CD是斜边AB上的中线,若∠A=20°,则∠BDC的度数为( )
A. 30° B. 40° C. 45° D. 60°
3 (2025南京建邺期末)若直角三角形斜边上的中线与高的长分别是5和4,则这个三角形的面积是 .
4 (2024徐州铜山期中)如图,在△ABC中,AB=AC=8,AD是角平分线,BE是中线,则DE的长为 .
5 如图,AD是△ABC的中线,DE是△ADC的高,AB=16,AC=22,DE=8,则点D到AB的距离是 .
6 如图,∠ABC=∠ADC=90°,E,F分别是AC,BD的中点,求证:EF⊥BD.
7 (2024东台期末)如图,在△ABC中,CE,BD分别是边AB,AC上的高,M是BC的中点,连接DE,EM,MD.
(1) 求证:ME=MD;
(2) 若∠A=45°,求∠EDM的度数.
建议用时:20+5分钟
8 (2025苏州期末)如图,在△ABC中,∠ACB=90°,D是边AB的中点,以点C为圆心,CD的长为半径画弧,与线段BD相交于另一点E,连接CE.若∠A=∠DCE,则∠A的度数为( )
A. 20° B. 30° C. 36° D. 40°
(第8题) (第9题) (第10题) (第11题)
9 如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,BD.若∠EBD=35°,则∠BAD的度数为( )
A. 55° B. 58° C. 65° D. 68°
10 (2024盐城建湖期末)如图,在四边形ABCD中,∠ABC=∠ADC=90°,∠BAD=45°,连接AC,BD,M是AC的中点,连接BM,DM.若△BMD的面积为32,则AC的长为 .
11 如图,在Rt△ABC中,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A的度数为 .
12 如图,在△ABC中,AD是高,CE是中线,G是CE的中点,DG⊥CE,垂足为G.
(1) 求证:DC=BE;
(2) 若∠AEC=75°,求∠BCE的度数.
13 (2025苏州期末)已知线段AC,以AC为斜边作Rt△ABC和Rt△ADC,连接BD,M,N分别是线段AC,BD的中点,连接MN,MB.
(1) 如图1,Rt△ABC和Rt△ADC在线段AC的两侧.
①求证:MN⊥BD;
②若∠BAC=45°,∠DAC=28°,请求出∠BMN的度数;
(2) 如图2,Rt△ABC和Rt△ADC在线段AC的同侧,若∠BAC=α,∠DAC=β(α>β),则∠BMN的度数为 (用含α,β的代数式表示).
图1 图2
1.5 等腰三角形
第1课时 等腰三角形的性质
1. B 2. A 3. 2 4. 40°或100° 5. 110°
6. 证明:过点A作AF⊥BC,垂足为F,
因为AB=AC,AF⊥BC,
所以BF=CF.
因为AD=AE,AF⊥DE,
所以DF=EF,
所以BF-DF=CF-EF,
所以BD=CE.
7. (1)证明:因为AD⊥BC,
所以∠B+∠BAD=90°.
因为CE⊥AB,
所以∠B+∠BCE=90°,
所以∠EAF=∠ECB.
在△AEF和△CEB中,
所以△AEF≌△CEB(ASA).
(2) 解:因为△AEF≌△CEB,
所以AF=BC.
因为AB=AC,AD⊥BC,
所以CD=BD,BC=2CD,
所以AF=2CD,
所以CD=AF=×6=3.
8. A 9. D 10. 60°或120° 11. 67°
12. 解:(1) ①40°
②∠C=2∠D,理由如下:
因为AD∥BC,
所以∠D=∠DBC,
又因为AB=AD,
所以∠D=∠ABD,
所以∠ABC=2∠D.
因为AB=AC,
所以∠C=∠ABC=2∠D.
(2) AD∥BC,证明如下:
因为AB=AC,∠C=2∠D,
所以∠ABC=∠C=2∠D.
因为AB=AD,
所以∠ABD=∠D,
所以∠DBC=∠D,
所以AD∥BC.
13. (1) 角平分线上的点到角的两边距离相等
(2) 证明:如图1,作DE⊥BA交BA的延长线于点E,DF⊥BC于点F.
因为BD平分∠EBF,DE⊥BE,DF⊥BF,
所以DE=DF.
因为∠BAD+∠C=180°,∠BAD+∠EAD=180°,
所以∠EAD=∠C.
在△DEA和△DFC中,
所以△DEA≌△DFC(AAS),
所以DA=DC.
(3) 证明:如图2,在BC上截取BK=BD,连接DK.
因为AB=AC,∠A=100°,
所以∠ABC=∠C=40°.
因为BD平分∠ABC,
所以∠DBK=∠ABC=20°.
因为BD=BK,
所以∠BKD=∠BDK=80°,即∠A+∠BKD=180°,
由(2)的结论得AD=DK,
因为∠BKD=∠C+∠KDC,
所以∠KDC=∠C=40°,
所以DK=CK,
所以AD=DK=CK,
所以BD+AD=BK+CK=BC.
图1 图2
第2课时 等腰三角形的判定
1. C 2. B 3. D 4. 2 5. 10
6. 证明:因为∠ACB=90°,CD⊥AB,
所以∠CBF+∠CFB=∠DBE+∠DEB=90°.
因为BF平分∠ABC,
所以∠CBF=∠DBE,
所以∠CFB=∠DEB.
又因为∠FEC=∠DEB,
所以∠CFB=∠FEC,
所以CE=CF.
7. (1) 证明:因为AF平分∠DAC,
所以∠DAF=∠CAF.
因为AF∥BC,
所以∠DAF=∠B,∠CAF=∠ACB,
所以∠B=∠ACB,
所以AB=AC,即△ABC是等腰三角形.
(2) 解:因为AB=AC,∠B=40°,
所以∠ACB=∠B=40°,
所以∠ACE=180°-∠ACB=140°.
因为CG平分∠ACE,
所以∠ACG=∠GCE=∠ACE=70°.
因为AF∥BC,
所以∠AGC=∠GCE=70°.
8. D 9. 8 10. 2
11. 解:(1) 因为BP,CP分别是∠ABC和∠ACB的平分线,
所以∠ABP=∠PBD,∠ACP=∠PCE.
因为PD∥AB,PE∥AC,
所以∠ABP=∠BPD,∠ACP=∠CPE,
所以∠PBD=∠BPD,∠PCE=∠CPE,
所以BD=PD,CE=PE,
所以△PDE的周长=PD+DE+PE=BD+DE+EC=BC=8 cm.
(2) 因为∠A=50°,
所以∠ABC+∠ACB=130°,
所以∠ABC+∠ACB=65°.
因为BP,CP分别是∠ABC和∠ACB的平分线,
所以∠PBC=∠ABC,∠PCB=∠ACB,
所以∠PBC+∠PCB=65°,
所以∠BPC=180°-65°=115°.
12. (1) 证明:因为AB=AC,
所以∠ABC=∠ACB.
因为∠BDC是△ADC的一个外角,
所以∠BDC=∠A+∠ACD.
因为∠ACB=∠BCD+∠ACD,∠BCD=∠A,
所以∠BDC=∠ACB,
所以∠ABC=∠BDC.
所以CD=CB.
(2) ①证明:因为BE⊥AC,
所以∠BEC=90°,
所以∠CBE+∠ACB=90°.
设∠CBE=α,则∠ACB=90°-α,
所以∠ACB=∠ABC=∠BDC=90°-α,
所以∠BCD=180°-∠BDC-∠ABC=180°-(90°-α)-(90°-α)=2α,
所以∠BCD=2∠CBE.
②解:因为∠BFD是△CBF的一个外角,
所以∠BFD=∠CBE+∠BCD=α+2α=3α.
当BD=BF时,∠BDC=∠BFD=3α,
因为∠ACB=∠ABC=∠BDC=90°-α,
所以90°-α=3α,
所以α=22.5°,
所以∠A=∠BCD=2α=45°;
当DB=DF时,∠DBE=∠BFD=3α,
因为∠DBE=∠ABC-∠CBE=90°-α-α=90°-2α,
所以90°-2α=3α,
所以α=18°,
所以∠A=∠BCD=2α=36°;
当FB=FD时,∠DBE=∠BDF,
因为∠BDF=∠ABC>∠DBF,
所以不存在FB=FD.
综上,∠A的度数为45°或36°.
第3课时 等边三角形的判定与性质
1. C 2. C 3. 8 4. 60° 5. 102°
6. (1) 证明:因为△ABC为等边三角形,
所以AB=BC=CA,∠BAC=∠BCA=60°.
因为BM=CN,
所以CM=AN.
在△BAN和△ACM中,
所以△BAN≌△ACM(SAS).
(2) 解:因为△BAN≌△ACM,
所以∠CAM=∠ABN,
所以∠BQM=∠ABN+∠BAQ=∠CAM+∠BAQ=∠BAC=60°.
7. (1) 解:因为AB=AC,∠BAC=120°,
所以∠B=∠C=30°.
因为AE=BE,所以∠B=∠EAB=30°.
因为∠BAC=120°,所以∠CAE=∠BAC-∠EAB=90°,
即∠CAE=90°.
(2) 证明:由(1),得∠CAE=90°,∠C=30°,
所以∠AED=60°,所以AE=EC.
因为D为线段EC的中点,
所以ED=EC,
所以AE=ED,则△ADE是等边三角形.
8. A 9. D 10. 2 11. 2n-1
12. (1) 证明:因为△ABD,△BCE都是等边三角形,
所以AB=BD,BC=BE,∠ABD=∠CBE=60°,
所以∠ABD+∠DBE=∠DBE+∠CBE,即∠ABE=∠DBC.
在△ABE和△DBC中,
所以△ABE≌△DBC(SAS),
所以AE=CD.
(2) 解:△BMN是等边三角形,理由如下:
因为△ABE≌△DBC,
所以∠BAE=∠BDC.
因为AE=CD,M,N分别是AE,CD的中点,
所以AM=AE=CD=DN.
在△ABM和△DBN中,
所以△ABM≌△DBN(SAS),
所以BM=BN,∠ABM=∠DBN,
所以∠DBM+∠DBN=∠DBM+∠ABM=∠ABD=60°,
即∠MBN=60°,
所以△BMN是等边三角形.
13. (1) 证明:因为△ABC为等边三角形,
所以∠ABC=∠A=∠ACB=60°.
因为E为AB的中点,
所以CE⊥AB,CE是∠ACB的平分线,
所以∠BEC=90°,∠BCE=30°,
所以2EB=BC.
因为ED=EC,
所以∠EDC=∠ECD=30°,
所以∠DEB=∠ABC-∠EDC=60°-30°=30°,
所以BD=BE,
所以2BD=BC.
(2) 解:如图,过点E作EF∥BC,交AC于点F.
因为△ABC为等边三角形,
所以∠A=∠AFE=∠ACB=∠ABC=60°,
所以△AEF为等边三角形,
所以∠EFC=∠EBD=120°,EF=AE.
因为ED=EC,
所以∠EDB=∠ECB,∠ECB=∠FEC,
所以∠EDB=∠FEC.
在△BDE和△FEC中,
所以△BDE≌△FEC(AAS),
所以BD=EF,
所以AE=BD=2,
所以CD=BC+BD=12+2=14.
第4课时 直角三角形的性质
1. A 2. B 3. 20 4. 4 5. 11
6. 证明:连接DE,BE.
因为∠ABC=∠ADC=90°,E为AC的中点,
所以BE=AC,DE=AC,所以BE=DE.
因为F为BD的中点,所以EF⊥BD.
7. (1) 证明:因为CE,BD分别是边AB,AC上的高,
所以∠BEC=∠CDB=90°.
因为M是BC的中点,
所以EM=BC,DM=BC,所以ME=MD.
(2) 解:因为∠A=45°,
所以∠ABC+∠ACB=180°-∠A=135°.
因为∠BEC=∠CDB=90°,M为BC的中点,
所以EM=BM,DM=CM,
所以∠BEM=∠ABC,∠MDC=∠ACB,
所以∠ABC+∠BEM+∠ACB+∠MDC=135°×2=270°,
所以∠EMB+∠DMC=180°×2-270°=90°,
所以∠EMD=180°-(∠EMB+∠DMC)=180°-90°=90°.
因为ME=MD,所以∠EDM=45°.
8. C 9. A 10. 16 11. 30°
12. (1) 证明:连接ED.因为G是CE的中点,DG⊥CE,
所以DE=DC.
因为AD是高,所以△ABD是直角三角形.
又因为CE是中线,所以E是AB的中点,
所以ED是Rt△ABD的中线,
所以DE=BE=AE,所以BE=CD.
(2) 解:因为DE=BE=AE=DC,
所以∠BCE=∠DEC,∠BAD=∠ADE,
所以∠EDB=2∠BCE,
∠ADE=
==.
因为AD是高,所以∠EDB+∠ADE=90°,
即2∠BCE+=90°,
所以3∠BCE=75°,所以∠BCE=25°.
13. (1) ①证明:如图1,连接MD.
因为∠ABC=∠ADC=90°,M是AC的中点,
所以BM=AC,DM=AC,
所以BM=DM.
又因为N是BD的中点,
所以MN⊥BD.
②解:因为∠ABC=∠ADC=90°,M是AC的中点,
所以BM=AM=MC=DM.
又因为∠BAC=45°,∠DAC=28°,
所以∠MBC=∠MCB=90°-∠BAC=45°,∠MCD=∠CDM=90°-∠DAC=62°,
所以∠BMD=360°-45°×2-62°×2=146°.
因为BM=DM,MN⊥BD,
所以∠BMN=∠DMN=∠BMD=×146°=73°.
(2) α-β 提示:如图2,连接MD,因为∠ABC=∠ADC=90°,M是AC的中点,所以AM=BM=MD,所以∠MBA=∠BAC=α,∠MDA=∠DAC=β,所以∠AMB=180°-2α,∠CMD=2β,所以∠BMD=180°-∠AMB-∠CMD=2α-2β.因为BM=MD,N是BD的中点,所以∠BMN=∠DMN=∠BMD=(2α-2β)=α-β.
图1 图2
同课章节目录
