3.1 勾 股 定 理 同步练 (含答案)2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 3.1 勾 股 定 理 同步练 (含答案)2025-2026学年数学苏科版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 252.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 15:30:00 | ||
图片预览

文档简介
3.1 勾 股 定 理
第1课时 勾股定理的发现
掌握勾股定理,会用勾股定理解决问题.
建议用时:15分钟
1 (2025无锡期末)在Rt△ABC中,∠C=90°,若AC=4,则AB2-BC2等于( )
A. 4 B. 16 C. 20 D. 25
2 在△ABC中,角A,B,C所对的边分别为a,b,c,则下列说法中正确的是( )
A. 若∠A=90°,则a2+b2=c2 B. 若∠B=90°,则a2+b2=c2
C. 若∠C=90°,则a2+c2=b2 D. 若∠A=90°,则c2+b2=a2
3 (1) 在△ABC中,∠C=90°,若c=13,b=12,则a= ;
(2) 在△ABC中,∠C=90°,若a∶b=3∶4,c=10,则a= ,b= .
(3) (2025无锡梁溪期末)如果直角三角形的两条边长分别为2和3,那么它的第三条边长为 .
4 (2025盐城盐都期末)如图,在Rt△ABC中,∠C=90°,BC>AC,以AB,BC,AC三边为边长的三个正方形面积分别为S1,S2,S3.若AB=5,S3=5,则S2的值为 .
(第4题) (第5题) (第6题)
5 (教材P88例2变式)如图,网格中每个小正方形的边长均为1,点A,B,C都在格点上,以点A为圆心,AB为半径画弧,交最上方的网格线于点D,则CD的长为 .
6 (2025宿迁宿豫期末)如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE∥AB交AC于点E.若CE=1,CD=,则AE的长为 .
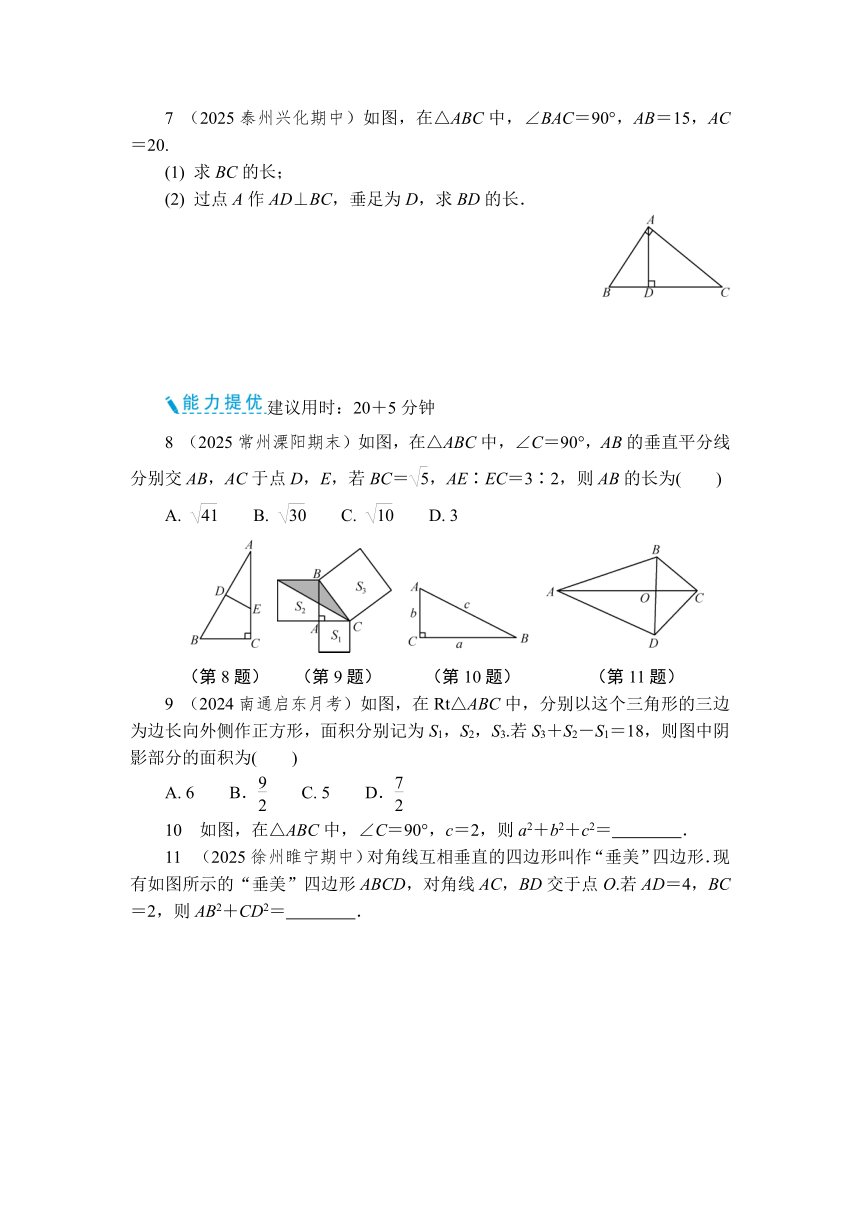
7 (2025泰州兴化期中)如图,在△ABC中,∠BAC=90°,AB=15,AC=20.
(1) 求BC的长;
(2) 过点A作AD⊥BC,垂足为D,求BD的长.
建议用时:20+5分钟
8 (2025常州溧阳期末)如图,在△ABC中,∠C=90°,AB的垂直平分线分别交AB,AC于点D,E,若BC=,AE∶EC=3∶2,则AB的长为( )
A. B. C. D. 3
(第8题) (第9题) (第10题) (第11题)
9 (2024南通启东月考)如图,在Rt△ABC中,分别以这个三角形的三边为边长向外侧作正方形,面积分别记为S1,S2,S3.若S3+S2-S1=18,则图中阴影部分的面积为( )
A. 6 B. C. 5 D.
10 如图,在△ABC中,∠C=90°,c=2,则a2+b2+c2= .
11 (2025徐州睢宁期中)对角线互相垂直的四边形叫作“垂美”四边形.现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O.若AD=4,BC=2,则AB2+CD2= .
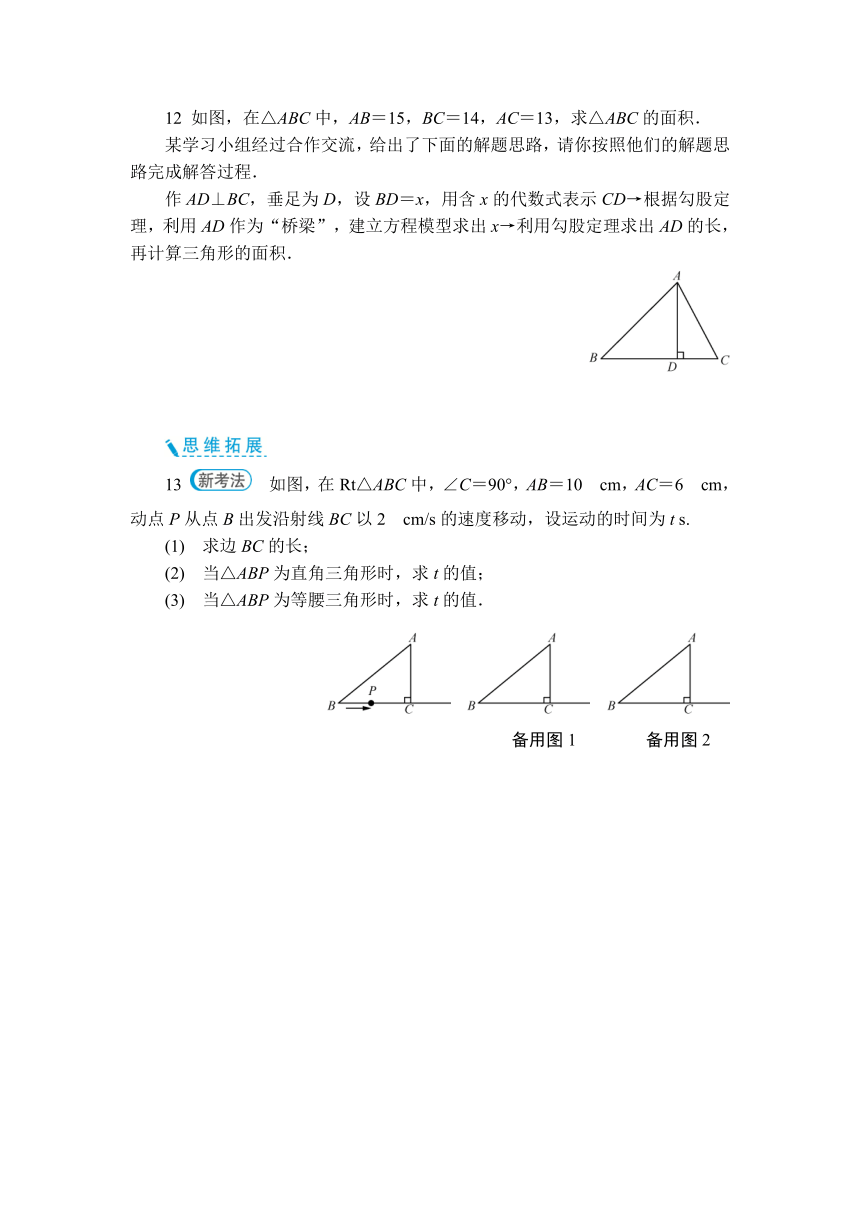
12 如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
作AD⊥BC,垂足为D,设BD=x,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,建立方程模型求出x→利用勾股定理求出AD的长,再计算三角形的面积.
13 如图,在Rt△ABC中,∠C=90°,AB=10 cm,AC=6 cm,动点P从点B出发沿射线BC以2 cm/s的速度移动,设运动的时间为t s.
(1) 求边BC的长;
(2) 当△ABP为直角三角形时,求t的值;
(3) 当△ABP为等腰三角形时,求t的值.
备用图1 备用图2
第2课时 勾股定理的证明
能够利用面积法进行勾股定理的证明.
建议用时:15分钟
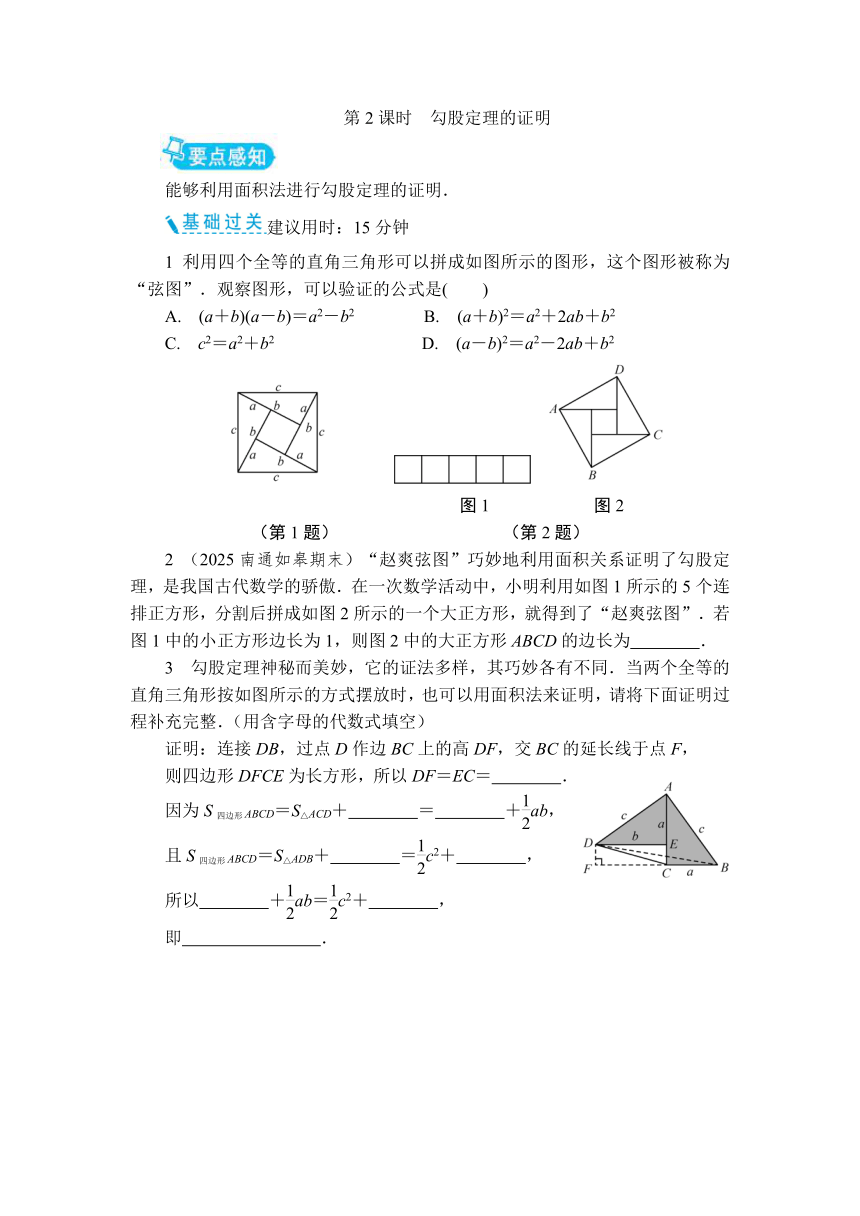
1 利用四个全等的直角三角形可以拼成如图所示的图形,这个图形被称为“弦图”.观察图形,可以验证的公式是( )
A. (a+b)(a-b)=a2-b2 B. (a+b)2=a2+2ab+b2
C. c2=a2+b2 D. (a-b)2=a2-2ab+b2
图1 图2
(第1题) (第2题)
2 (2025南通如皋期末)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.在一次数学活动中,小明利用如图1所示的5个连排正方形,分割后拼成如图2所示的一个大正方形,就得到了“赵爽弦图”.若图1中的小正方形边长为1,则图2中的大正方形ABCD的边长为 .
3 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同.当两个全等的直角三角形按如图所示的方式摆放时,也可以用面积法来证明,请将下面证明过程补充完整.(用含字母的代数式填空)
证明:连接DB,过点D作边BC上的高DF,交BC的延长线于点F,
则四边形DFCE为长方形,所以DF=EC= .
因为S四边形ABCD=S△ACD+ = +ab,
且S四边形ABCD=S△ADB+ =c2+ ,
所以 +ab=c2+ ,
即 .
4 如图,对任意符合条件的Rt△ABC,绕其锐角顶点A逆时针旋转90°得到Rt△AED(∠BAE=90°),连接BE,延长DE,BC,交于点F,易知四边形ACFD是一个正方形,它的面积和四边形ABFE的面积相等,四边形ABFE的面积等于Rt△BAE和Rt△BFE的面积之和,根据图形写出一种证明勾股定理的方法.
建议用时:20+5分钟
5 (2024南通)“赵爽弦图”巧妙利用面积关系证明了勾股定理.如图所示的“赵爽弦图”是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形.设直角三角形的两条直角边长分别为m,n(m>n).若小正方形面积为5,且(m+n)2=21,则大正方形面积为( )
A. 12 B. 13 C. 14 D. 15
(第5题) (第7题)
6 若n>1,△ABC三边长分别是n2-1,2n,n2+1,则△ABC是 三角形.
7 如图所示的图形表示勾股定理的一种证明方法,该方法运用了祖冲之的出入相补原理.若图中空白部分的面积是14,整个图形(连同空白部分)的面积是36,则大正方形ABCD的边长是 .
8 勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若鹜,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.证法如下:把两个全等的直角三角形(Rt△ABC≌Rt△DAE)按如图所示的方式放置,∠DAB=∠B=90°,点E在边AB上,现设Rt△ABC的两直角边长分别为CB=b,AB=a,斜边长为AC=c.
(1) 求证:AC⊥DE;
(2) 请根据上述图形的面积关系证明勾股定理.
9 如图,在△ABD中,AC⊥BD于点C,E为AC上的一点,连接BE,DE,DE的延长线交AB于点F.已知DE=AB,∠CAD=45°.
(1) 求证:DF⊥AB;
(2) 利用图中阴影部分面积完成勾股定理的证明.如图,在△ABC中,∠ACB=90°,BC=a,AC=b,AB=c,求证:a2+b2=c2.
3.1 勾 股 定 理
第1课时 勾股定理的发现
1. B 2. D 3. (1) 5 (2) 6 8 (3) 或 4. 20 5. 3- 6. 2
7. 解:(1) 在△ABC中,∠BAC=90°,AB=15,AC=20,
所以BC===25.
(2) 因为AD⊥BC,
所以S△ABC=AB·AC=BC·AD,
所以AD===12,
所以BD===9.
8. B 9. B 10. 8 11. 20
12. 解:在△ABC中,AB=15,BC=14,AC=13,
设BD=x,则有CD=14-x.
由勾股定理,得AD2=AB2-BD2=152-x2,AD2=AC2-CD2=132-(14-x)2,
所以152-x2=132-(14-x)2,解得x=9,
所以AD=12,
所以S△ABC=BC·AD=×14×12=84.
13. 解:(1) 在Rt△ABC中,BC2=AB2-AC2=102-62=64,所以BC=8 cm.
(2) 由题意可知BP=2t cm.
①当∠APB为直角时,点P与点C重合,BP=BC=8 cm,即t=4;
②当∠BAP为直角时,BP=2t cm,CP=(2t-8) cm,AC=6 cm,
在Rt△ACP中,AP2=62+(2t-8)2,
在Rt△BAP中,AB2+AP2=BP2,即102+[62+(2t-8)2]=(2t)2,
解得t=.
综上,当△ABP为直角三角形时,t的值为4或.
(3) ①当AB=BP时,易得t=5;
②当AB=AP时,BP=2BC=16 cm,易得t=8;
③当BP=AP时,AP=BP=2t cm,CP=|2t-8| cm,AC=6 cm.
在Rt△ACP中,AP2=AC2+CP2,即(2t)2=62+(2t-8)2,解得t=.
综上,当△ABP为等腰三角形时,t的值为5或8或.
第2课时 勾股定理的证明
1. C 2.
3. b-a S△ABC b2 S△DCB a(b-a) b2
a(b-a) a2+b2=c2
4. 解:由题意,得S正方形ACFD=b2,
且S四边形ABFE=S△ABE+S△BEF=c2+(a+b)(b-a)=c2+b2-a2.
因为S正方形ACFD=S四边形ABFE,
所以c2+b2-a2=b2,
整理,得a2+b2=c2.
5. B 6. 直角 7. 5
8. 证明:(1) 因为Rt△ABC≌Rt△DAE,
所以∠ACB=∠DEA.
因为∠B=90°,
所以∠ACB+∠BAC=90°,
所以∠DEA+∠BAC=90°,
所以∠AFE=180°-∠BAC-∠DEA=90°,
所以AC⊥DE.
(2) 由题意,得S梯形ABCD=·AB=·a=a2+ab,
且S△CBE=BE·BC=b(a-b)=ab-b2.
因为Rt△ABC≌Rt△DAE,
所以DE=AC=c,
所以S四边形AECD=S△ADE+S△CDE
=AF·DE+CF·DE =AC·DE=c2,
所以ab-b2+c2=a2+ab,
整理,得a2+b2=c2.
9. 证明:(1) 因为AC⊥BD,∠CAD=45°,
所以AC=DC,∠ACB=∠DCE=90°.
在Rt△ABC与Rt△DEC中,
所以Rt△ABC≌Rt△DEC(HL),
所以∠BAC=∠EDC.
因为∠EDC+∠CED=90°,∠CED=∠AEF,
所以∠AEF+∠BAC=90°,
所以∠AFE=90°,所以DF⊥AB.
(2) 因为S△BCE+S△ACD=S△ABD-S△ABE,
所以a2+b2=c·DF-c·EF=c·(DF-EF)=c·DE=c2,
整理,得a2+b2=c2.
第1课时 勾股定理的发现
掌握勾股定理,会用勾股定理解决问题.
建议用时:15分钟
1 (2025无锡期末)在Rt△ABC中,∠C=90°,若AC=4,则AB2-BC2等于( )
A. 4 B. 16 C. 20 D. 25
2 在△ABC中,角A,B,C所对的边分别为a,b,c,则下列说法中正确的是( )
A. 若∠A=90°,则a2+b2=c2 B. 若∠B=90°,则a2+b2=c2
C. 若∠C=90°,则a2+c2=b2 D. 若∠A=90°,则c2+b2=a2
3 (1) 在△ABC中,∠C=90°,若c=13,b=12,则a= ;
(2) 在△ABC中,∠C=90°,若a∶b=3∶4,c=10,则a= ,b= .
(3) (2025无锡梁溪期末)如果直角三角形的两条边长分别为2和3,那么它的第三条边长为 .
4 (2025盐城盐都期末)如图,在Rt△ABC中,∠C=90°,BC>AC,以AB,BC,AC三边为边长的三个正方形面积分别为S1,S2,S3.若AB=5,S3=5,则S2的值为 .
(第4题) (第5题) (第6题)
5 (教材P88例2变式)如图,网格中每个小正方形的边长均为1,点A,B,C都在格点上,以点A为圆心,AB为半径画弧,交最上方的网格线于点D,则CD的长为 .
6 (2025宿迁宿豫期末)如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE∥AB交AC于点E.若CE=1,CD=,则AE的长为 .
7 (2025泰州兴化期中)如图,在△ABC中,∠BAC=90°,AB=15,AC=20.
(1) 求BC的长;
(2) 过点A作AD⊥BC,垂足为D,求BD的长.
建议用时:20+5分钟
8 (2025常州溧阳期末)如图,在△ABC中,∠C=90°,AB的垂直平分线分别交AB,AC于点D,E,若BC=,AE∶EC=3∶2,则AB的长为( )
A. B. C. D. 3
(第8题) (第9题) (第10题) (第11题)
9 (2024南通启东月考)如图,在Rt△ABC中,分别以这个三角形的三边为边长向外侧作正方形,面积分别记为S1,S2,S3.若S3+S2-S1=18,则图中阴影部分的面积为( )
A. 6 B. C. 5 D.
10 如图,在△ABC中,∠C=90°,c=2,则a2+b2+c2= .
11 (2025徐州睢宁期中)对角线互相垂直的四边形叫作“垂美”四边形.现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O.若AD=4,BC=2,则AB2+CD2= .
12 如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
作AD⊥BC,垂足为D,设BD=x,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,建立方程模型求出x→利用勾股定理求出AD的长,再计算三角形的面积.
13 如图,在Rt△ABC中,∠C=90°,AB=10 cm,AC=6 cm,动点P从点B出发沿射线BC以2 cm/s的速度移动,设运动的时间为t s.
(1) 求边BC的长;
(2) 当△ABP为直角三角形时,求t的值;
(3) 当△ABP为等腰三角形时,求t的值.
备用图1 备用图2
第2课时 勾股定理的证明
能够利用面积法进行勾股定理的证明.
建议用时:15分钟
1 利用四个全等的直角三角形可以拼成如图所示的图形,这个图形被称为“弦图”.观察图形,可以验证的公式是( )
A. (a+b)(a-b)=a2-b2 B. (a+b)2=a2+2ab+b2
C. c2=a2+b2 D. (a-b)2=a2-2ab+b2
图1 图2
(第1题) (第2题)
2 (2025南通如皋期末)“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.在一次数学活动中,小明利用如图1所示的5个连排正方形,分割后拼成如图2所示的一个大正方形,就得到了“赵爽弦图”.若图1中的小正方形边长为1,则图2中的大正方形ABCD的边长为 .
3 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同.当两个全等的直角三角形按如图所示的方式摆放时,也可以用面积法来证明,请将下面证明过程补充完整.(用含字母的代数式填空)
证明:连接DB,过点D作边BC上的高DF,交BC的延长线于点F,
则四边形DFCE为长方形,所以DF=EC= .
因为S四边形ABCD=S△ACD+ = +ab,
且S四边形ABCD=S△ADB+ =c2+ ,
所以 +ab=c2+ ,
即 .
4 如图,对任意符合条件的Rt△ABC,绕其锐角顶点A逆时针旋转90°得到Rt△AED(∠BAE=90°),连接BE,延长DE,BC,交于点F,易知四边形ACFD是一个正方形,它的面积和四边形ABFE的面积相等,四边形ABFE的面积等于Rt△BAE和Rt△BFE的面积之和,根据图形写出一种证明勾股定理的方法.
建议用时:20+5分钟
5 (2024南通)“赵爽弦图”巧妙利用面积关系证明了勾股定理.如图所示的“赵爽弦图”是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形.设直角三角形的两条直角边长分别为m,n(m>n).若小正方形面积为5,且(m+n)2=21,则大正方形面积为( )
A. 12 B. 13 C. 14 D. 15
(第5题) (第7题)
6 若n>1,△ABC三边长分别是n2-1,2n,n2+1,则△ABC是 三角形.
7 如图所示的图形表示勾股定理的一种证明方法,该方法运用了祖冲之的出入相补原理.若图中空白部分的面积是14,整个图形(连同空白部分)的面积是36,则大正方形ABCD的边长是 .
8 勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若鹜,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.证法如下:把两个全等的直角三角形(Rt△ABC≌Rt△DAE)按如图所示的方式放置,∠DAB=∠B=90°,点E在边AB上,现设Rt△ABC的两直角边长分别为CB=b,AB=a,斜边长为AC=c.
(1) 求证:AC⊥DE;
(2) 请根据上述图形的面积关系证明勾股定理.
9 如图,在△ABD中,AC⊥BD于点C,E为AC上的一点,连接BE,DE,DE的延长线交AB于点F.已知DE=AB,∠CAD=45°.
(1) 求证:DF⊥AB;
(2) 利用图中阴影部分面积完成勾股定理的证明.如图,在△ABC中,∠ACB=90°,BC=a,AC=b,AB=c,求证:a2+b2=c2.
3.1 勾 股 定 理
第1课时 勾股定理的发现
1. B 2. D 3. (1) 5 (2) 6 8 (3) 或 4. 20 5. 3- 6. 2
7. 解:(1) 在△ABC中,∠BAC=90°,AB=15,AC=20,
所以BC===25.
(2) 因为AD⊥BC,
所以S△ABC=AB·AC=BC·AD,
所以AD===12,
所以BD===9.
8. B 9. B 10. 8 11. 20
12. 解:在△ABC中,AB=15,BC=14,AC=13,
设BD=x,则有CD=14-x.
由勾股定理,得AD2=AB2-BD2=152-x2,AD2=AC2-CD2=132-(14-x)2,
所以152-x2=132-(14-x)2,解得x=9,
所以AD=12,
所以S△ABC=BC·AD=×14×12=84.
13. 解:(1) 在Rt△ABC中,BC2=AB2-AC2=102-62=64,所以BC=8 cm.
(2) 由题意可知BP=2t cm.
①当∠APB为直角时,点P与点C重合,BP=BC=8 cm,即t=4;
②当∠BAP为直角时,BP=2t cm,CP=(2t-8) cm,AC=6 cm,
在Rt△ACP中,AP2=62+(2t-8)2,
在Rt△BAP中,AB2+AP2=BP2,即102+[62+(2t-8)2]=(2t)2,
解得t=.
综上,当△ABP为直角三角形时,t的值为4或.
(3) ①当AB=BP时,易得t=5;
②当AB=AP时,BP=2BC=16 cm,易得t=8;
③当BP=AP时,AP=BP=2t cm,CP=|2t-8| cm,AC=6 cm.
在Rt△ACP中,AP2=AC2+CP2,即(2t)2=62+(2t-8)2,解得t=.
综上,当△ABP为等腰三角形时,t的值为5或8或.
第2课时 勾股定理的证明
1. C 2.
3. b-a S△ABC b2 S△DCB a(b-a) b2
a(b-a) a2+b2=c2
4. 解:由题意,得S正方形ACFD=b2,
且S四边形ABFE=S△ABE+S△BEF=c2+(a+b)(b-a)=c2+b2-a2.
因为S正方形ACFD=S四边形ABFE,
所以c2+b2-a2=b2,
整理,得a2+b2=c2.
5. B 6. 直角 7. 5
8. 证明:(1) 因为Rt△ABC≌Rt△DAE,
所以∠ACB=∠DEA.
因为∠B=90°,
所以∠ACB+∠BAC=90°,
所以∠DEA+∠BAC=90°,
所以∠AFE=180°-∠BAC-∠DEA=90°,
所以AC⊥DE.
(2) 由题意,得S梯形ABCD=·AB=·a=a2+ab,
且S△CBE=BE·BC=b(a-b)=ab-b2.
因为Rt△ABC≌Rt△DAE,
所以DE=AC=c,
所以S四边形AECD=S△ADE+S△CDE
=AF·DE+CF·DE =AC·DE=c2,
所以ab-b2+c2=a2+ab,
整理,得a2+b2=c2.
9. 证明:(1) 因为AC⊥BD,∠CAD=45°,
所以AC=DC,∠ACB=∠DCE=90°.
在Rt△ABC与Rt△DEC中,
所以Rt△ABC≌Rt△DEC(HL),
所以∠BAC=∠EDC.
因为∠EDC+∠CED=90°,∠CED=∠AEF,
所以∠AEF+∠BAC=90°,
所以∠AFE=90°,所以DF⊥AB.
(2) 因为S△BCE+S△ACD=S△ABD-S△ABE,
所以a2+b2=c·DF-c·EF=c·(DF-EF)=c·DE=c2,
整理,得a2+b2=c2.
同课章节目录
