3.3 勾股定理的简单应用 同步练 (含答案)2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 3.3 勾股定理的简单应用 同步练 (含答案)2025-2026学年数学苏科版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 294.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 15:30:18 | ||
图片预览



文档简介
3.3 勾股定理的简单应用
第1课时 勾股定理在实际生活中的应用
1. 能利用勾股定理及勾股定理的逆定理解决实际问题.
2. 能在实际问题中构造直角三角形解决实际问题.
建议用时:15分钟
1 (教材P98例1变式)如图,一棵树从3 m处折断了,树顶端和树底端的距离为4 m,那么这棵树原来的高度是( )
A. 8 m B. 5 m C. 9 m D. 7 m
(第1题) (第2题) (第3题)
2 如图,在A村与B村之间有一座大山,原来从A村到B村,需沿道路A→C→B(∠C=90°)绕过村庄间的大山,打通A,B间的隧道后,就可直接从A村到B村.已知AC=6 km,BC=8 km,则打通隧道后从A村到B村比原来减少的路程为( )
A. 2 km B. 3 km C. 4 km D. 5 km
3 如图,长3.4 m的梯子靠在墙上,梯子的底端和墙脚线的距离为1.6 m,则梯子顶端距离地面的高度MN为 m.
4 一艘船由A港沿北偏东60°方向航行30 km至B港,然后再沿北偏西30°方向航行40 km至C港,则A,C两港之间的距离为 km.
5 如图是一个滑梯示意图,左边是楼梯,右边是滑道,已知滑道AC与AE的长度一样,滑梯的高度BC=4 m,BE=1 m.求滑道AC的长.
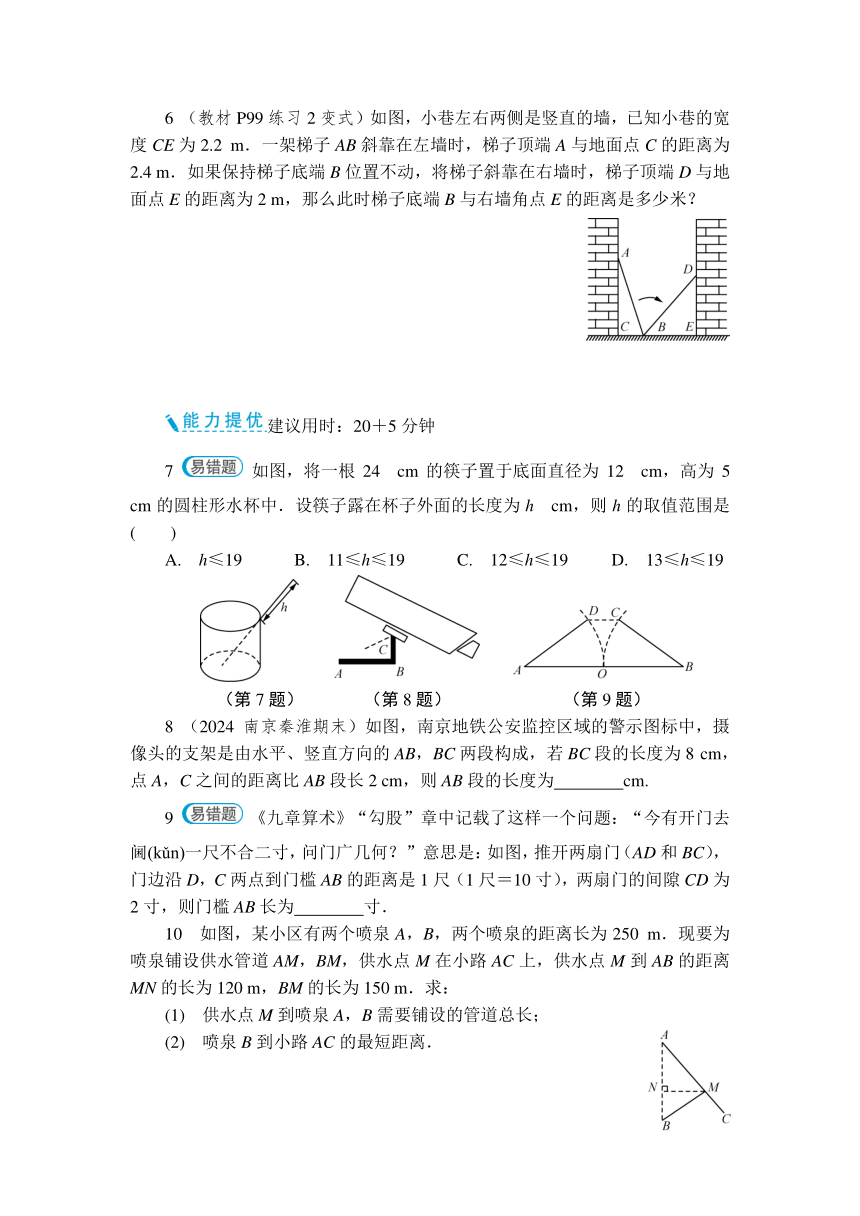
6 (教材P99练习2变式)如图,小巷左右两侧是竖直的墙,已知小巷的宽度CE为2.2 m.一架梯子AB斜靠在左墙时,梯子顶端A与地面点C的距离为2.4 m.如果保持梯子底端B位置不动,将梯子斜靠在右墙时,梯子顶端D与地面点E的距离为2 m,那么此时梯子底端B与右墙角点E的距离是多少米?
建议用时:20+5分钟
7 如图,将一根24 cm的筷子置于底面直径为12 cm,高为5 cm的圆柱形水杯中.设筷子露在杯子外面的长度为h cm,则h的取值范围是( )
A. h≤19 B. 11≤h≤19 C. 12≤h≤19 D. 13≤h≤19
(第7题) (第8题) (第9题)
8 (2024南京秦淮期末)如图,南京地铁公安监控区域的警示图标中,摄像头的支架是由水平、竖直方向的AB,BC两段构成,若BC段的长度为8 cm,点A,C之间的距离比AB段长2 cm,则AB段的长度为 cm.
9 《九章算术》“勾股”章中记载了这样一个问题:“今有开门去阃(kǔn)一尺不合二寸,问门广几何?”意思是:如图,推开两扇门(AD和BC),门边沿D,C两点到门槛AB的距离是1尺(1尺=10寸),两扇门的间隙CD为2寸,则门槛AB长为 寸.
10 如图,某小区有两个喷泉A,B,两个喷泉的距离长为250 m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN的长为120 m,BM的长为150 m.求:
(1) 供水点M到喷泉A,B需要铺设的管道总长;
(2) 喷泉B到小路AC的最短距离.
11 (2024广东期中)台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向,由点A向点B移动,已知点C为一海港,且点C与直线AB上两点A,B的距离CA,CB分别为300 km,400 km. AB=500 km,以台风中心为圆心,周围250 km以内为受影响区域.
(1) 海港C受台风影响吗?为什么?
(2) 如果台风中心移动的速度为20 km/h,那么台风影响海港C的持续时间有多长?
第2课时 勾股定理在几何图形中的应用
能利用勾股定理及勾股定理的逆定理解决几何问题.
建议用时:15分钟
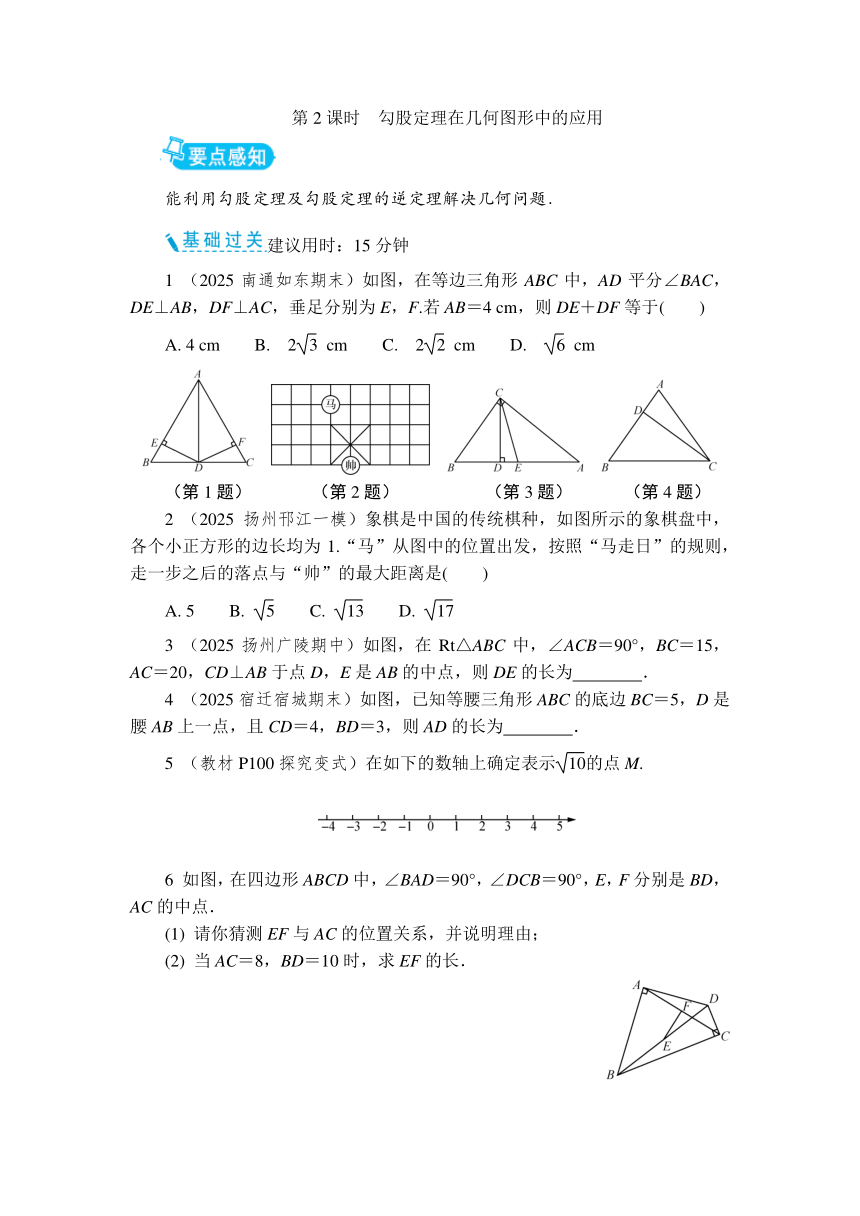
1 (2025南通如东期末)如图,在等边三角形ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E,F.若AB=4 cm,则DE+DF等于( )
A. 4 cm B. 2 cm C. 2 cm D. cm
(第1题) (第2题) (第3题) (第4题)
2 (2025扬州邗江一模)象棋是中国的传统棋种,如图所示的象棋盘中,各个小正方形的边长均为1.“马”从图中的位置出发,按照“马走日”的规则,走一步之后的落点与“帅”的最大距离是( )
A. 5 B. C. D.
3 (2025扬州广陵期中)如图,在Rt△ABC中,∠ACB=90°,BC=15,AC=20,CD⊥AB于点D,E是AB的中点,则DE的长为 .
4 (2025宿迁宿城期末)如图,已知等腰三角形ABC的底边BC=5,D是腰AB上一点,且CD=4,BD=3,则AD的长为 .
5 (教材P100探究变式)在如下的数轴上确定表示的点M.
6 如图,在四边形ABCD中,∠BAD=90°,∠DCB=90°,E,F分别是BD,AC的中点.
(1) 请你猜测EF与AC的位置关系,并说明理由;
(2) 当AC=8,BD=10时,求EF的长.
建议用时:20+5分钟
7 (2025苏州张家港月考)如图,在长方形ABCD中,AB=3 cm,AD=9 cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A. 3 cm2 B. 4 cm2 C. 6 cm2 D. 12 cm2
(第7题) (第8题) (第9题)
8 (2025浙江一模)如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中的阴影部分在数学史上被称为“希波克拉底月牙”.当AC=8,BC=4时,阴影部分的面积为 .
9 (2025泰州兴化期末)如图,在△ABC中,∠C=90°,AB=5,BC=3,若点P在边AC上运动,过点P作PQ⊥AB,垂足为Q,连接BP,则BP+PQ的最小值是 .
10 (2025苏州期中)如图,在△ABC中,E为边AB上的一点,连接CE并延长,过点A作AD⊥CE,垂足为D.已知AD=7,AB=20,BC=15,DC=24.
(1) 求证:∠B为直角;
(2) 记△ADE的面积为S1,△BCE的面积为S2,则S2-S1的值为 .
11 (2025扬州高邮期中)如图,在△ABC中,∠B=90°,AB=16 cm,BC=12 cm,M,N是△ABC边上的两个动点,其中点N从点A开始沿A→B方向运动,且速度为2 cm/s,点M从点B开始沿B→C→A方向运动,且速度为4 cm/s,它们同时出发,设运动的时间为t s.
(1) 出发2 s后,求MN的长;
(2) 当点M在边BC上运动时,出发几秒后,△MNB是等腰三角形?
(3) 当点M在边CA上运动时,求能使△BCM成为等腰三角形的t的值.
3.3 勾股定理的简单应用
第1课时 勾股定理在实际生活中的应用
1. A 2. C 3. 3 4. 50
5. 解:设AC=x m,则AE=AC=x m,AB=AE-BE=(x-1)m,
由题意,得∠ABC=90°,
在Rt△ABC中,由AB2+BC2=AC2,得(x-1)2+42=x2,
解得x=8.5,
所以滑道AC的长为8.5 m.
6. 解:设此时梯子底端B与右墙角点E的距离为x m,则BC=(2.2-x)m.
由题意可知AC=2.4 m,DE=2 m,AB=DB,
在Rt△ABC和Rt△DBE中,由勾股定理,得AB2=BC2+AC2,DB2=BE2+DE2,
所以BC2+AC2=BE2+DE2,
即(2.2-x)2+2.42=x2+4,
解得x=1.5,
故此时梯子底端B与右墙角点E的距离为1.5 m.
7. B 8. 15 9. 101
10. 解:(1) 在Rt△MNB中,由BN2=BM2-MN2,得BN=90(m),
所以AN=AB-BN=250-90=160(m).
在Rt△AMN中,由AM2=AN2+MN2,得AM=200(m),
所以供水点M到喷泉A,B需要铺设的管道总长=200+150=350(m).
(2) 因为AB=250 m,AM=200 m,BM=150 m,
所以AB2=BM2+AM2,
所以△ABM是直角三角形,且BM⊥AC,
所以喷泉B到小路AC的最短距离是BM=150 m.
11. 解:(1) 海港C受台风影响.理由如下:
如图,过点C作CD⊥AB于点D.
因为AC=300 km,BC=400 km,AB=500 km,
所以AC2+BC2=AB2,
所以△ABC是直角三角形,
所以S△ABC=×AC×BC=×CD×AB,
即300×400=500×CD,
所以CD==240(km),
因为以台风中心为圆心,周围250 km以内为受影响区域,
所以海港C受台风影响.
(2) 当EC=250 km,FC=250 km时,正好影响C海港,
因为ED==70(km),
所以EF=140 km.
因为台风中心移动的速度为20 km/h,
所以140÷20=7(h),
即台风影响海港C的持续时间为7 h.
第2课时 勾股定理在几何图形中的应用
1. B 2. A 3. 3.5 4.
5. 解:在数轴上画出点B表示3,作AB垂直于x轴,截取AB=1,根据勾股定理,得OA==,在数轴上用圆规截取OM=OA,点M表示的数就是.
6. 解:(1) EF⊥AC.理由如下:
连接AE,CE.
因为∠BAD=90°,E为边BD的中点,
所以AE=BD.
因为∠DCB=90°,E为边BD的中点,
所以CE=BD,
所以AE=CE.
因为F是AC的中点,
所以EF⊥AC.
(2) 因为AC=8,BD=10,E,F分别是边BD,AC的中点,
所以AE=CE=5,CF=4.
因为EF⊥AC,
所以EF===3.
7. C 8. 16 9.
10. (1) 证明:因为AD⊥CE,
所以∠D=90°.
因为AD=7,DC=24,
所以AC2=AD2+DC2=625=252.
因为AB=20,BC=15,202+152=252,
所以AB2+BC2=AC2,
所以△ABC是直角三角形,且∠B为直角.
(2) 66
11. 解:(1) 当t=2时,AN=2t=4 cm,BM=4t=8 cm.
因为AB=16 cm,
所以BN=AB-AN=16-4=12(cm).
在Rt△MNB中,由勾股定理可得
MN===(cm),
即MN的长为 cm.
(2) 由题意可知AN=2t cm,BM=4t cm,
又因为AB=16 cm,
所以BN=AB-AN=(16-2t)cm.
当△MNB为等腰三角形时,有BM=BN,
所以16-2t=4t,解得t=,
所以出发 s后△MNB是等腰三角形.
(3) 在△ABC中,由勾股定理可求得AC=20 cm,
当点M在AC上运动时,CM=(4t-12)cm.
因为△BCM为等腰三角形,
所以有BM=BC,CM=BC和CM=BM三种情况:
①当BM=BC=12 cm时,如图,过点B作BE⊥AC,
则CE=CM=2t-6.
在Rt△ABC中,由S△ABC=AB·BC=BE·AC,
得BE==9.6.
在Rt△BCE中,由勾股定理可得BC2=BE2+CE2,
即122=(9.6)2+(2t-6)2,
即(2t-6)2=7.22,
即2t-6=7.2或2t-6=-7.2,
解得t=6.6或t=-0.6(舍去).
②当CM=BC=12 cm时,则4t-12=12,解得t=6.
③当CM=BM时,即∠C=∠MBC,
因为∠C+∠A=90°=∠CBM+∠MBA,
所以∠A=∠MBA,
所以MB=MA,所以CM=AM=10 cm,
即4t-12=10,解得t=5.5.
综上,当t的值为6.6或6或5.5时,△BCM为等腰三角形.
第1课时 勾股定理在实际生活中的应用
1. 能利用勾股定理及勾股定理的逆定理解决实际问题.
2. 能在实际问题中构造直角三角形解决实际问题.
建议用时:15分钟
1 (教材P98例1变式)如图,一棵树从3 m处折断了,树顶端和树底端的距离为4 m,那么这棵树原来的高度是( )
A. 8 m B. 5 m C. 9 m D. 7 m
(第1题) (第2题) (第3题)
2 如图,在A村与B村之间有一座大山,原来从A村到B村,需沿道路A→C→B(∠C=90°)绕过村庄间的大山,打通A,B间的隧道后,就可直接从A村到B村.已知AC=6 km,BC=8 km,则打通隧道后从A村到B村比原来减少的路程为( )
A. 2 km B. 3 km C. 4 km D. 5 km
3 如图,长3.4 m的梯子靠在墙上,梯子的底端和墙脚线的距离为1.6 m,则梯子顶端距离地面的高度MN为 m.
4 一艘船由A港沿北偏东60°方向航行30 km至B港,然后再沿北偏西30°方向航行40 km至C港,则A,C两港之间的距离为 km.
5 如图是一个滑梯示意图,左边是楼梯,右边是滑道,已知滑道AC与AE的长度一样,滑梯的高度BC=4 m,BE=1 m.求滑道AC的长.
6 (教材P99练习2变式)如图,小巷左右两侧是竖直的墙,已知小巷的宽度CE为2.2 m.一架梯子AB斜靠在左墙时,梯子顶端A与地面点C的距离为2.4 m.如果保持梯子底端B位置不动,将梯子斜靠在右墙时,梯子顶端D与地面点E的距离为2 m,那么此时梯子底端B与右墙角点E的距离是多少米?
建议用时:20+5分钟
7 如图,将一根24 cm的筷子置于底面直径为12 cm,高为5 cm的圆柱形水杯中.设筷子露在杯子外面的长度为h cm,则h的取值范围是( )
A. h≤19 B. 11≤h≤19 C. 12≤h≤19 D. 13≤h≤19
(第7题) (第8题) (第9题)
8 (2024南京秦淮期末)如图,南京地铁公安监控区域的警示图标中,摄像头的支架是由水平、竖直方向的AB,BC两段构成,若BC段的长度为8 cm,点A,C之间的距离比AB段长2 cm,则AB段的长度为 cm.
9 《九章算术》“勾股”章中记载了这样一个问题:“今有开门去阃(kǔn)一尺不合二寸,问门广几何?”意思是:如图,推开两扇门(AD和BC),门边沿D,C两点到门槛AB的距离是1尺(1尺=10寸),两扇门的间隙CD为2寸,则门槛AB长为 寸.
10 如图,某小区有两个喷泉A,B,两个喷泉的距离长为250 m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN的长为120 m,BM的长为150 m.求:
(1) 供水点M到喷泉A,B需要铺设的管道总长;
(2) 喷泉B到小路AC的最短距离.
11 (2024广东期中)台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力.如图,有一台风中心沿东西方向,由点A向点B移动,已知点C为一海港,且点C与直线AB上两点A,B的距离CA,CB分别为300 km,400 km. AB=500 km,以台风中心为圆心,周围250 km以内为受影响区域.
(1) 海港C受台风影响吗?为什么?
(2) 如果台风中心移动的速度为20 km/h,那么台风影响海港C的持续时间有多长?
第2课时 勾股定理在几何图形中的应用
能利用勾股定理及勾股定理的逆定理解决几何问题.
建议用时:15分钟
1 (2025南通如东期末)如图,在等边三角形ABC中,AD平分∠BAC,DE⊥AB,DF⊥AC,垂足分别为E,F.若AB=4 cm,则DE+DF等于( )
A. 4 cm B. 2 cm C. 2 cm D. cm
(第1题) (第2题) (第3题) (第4题)
2 (2025扬州邗江一模)象棋是中国的传统棋种,如图所示的象棋盘中,各个小正方形的边长均为1.“马”从图中的位置出发,按照“马走日”的规则,走一步之后的落点与“帅”的最大距离是( )
A. 5 B. C. D.
3 (2025扬州广陵期中)如图,在Rt△ABC中,∠ACB=90°,BC=15,AC=20,CD⊥AB于点D,E是AB的中点,则DE的长为 .
4 (2025宿迁宿城期末)如图,已知等腰三角形ABC的底边BC=5,D是腰AB上一点,且CD=4,BD=3,则AD的长为 .
5 (教材P100探究变式)在如下的数轴上确定表示的点M.
6 如图,在四边形ABCD中,∠BAD=90°,∠DCB=90°,E,F分别是BD,AC的中点.
(1) 请你猜测EF与AC的位置关系,并说明理由;
(2) 当AC=8,BD=10时,求EF的长.
建议用时:20+5分钟
7 (2025苏州张家港月考)如图,在长方形ABCD中,AB=3 cm,AD=9 cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
A. 3 cm2 B. 4 cm2 C. 6 cm2 D. 12 cm2
(第7题) (第8题) (第9题)
8 (2025浙江一模)如图,在Rt△ABC中,∠C=90°,分别以各边为直径作半圆,图中的阴影部分在数学史上被称为“希波克拉底月牙”.当AC=8,BC=4时,阴影部分的面积为 .
9 (2025泰州兴化期末)如图,在△ABC中,∠C=90°,AB=5,BC=3,若点P在边AC上运动,过点P作PQ⊥AB,垂足为Q,连接BP,则BP+PQ的最小值是 .
10 (2025苏州期中)如图,在△ABC中,E为边AB上的一点,连接CE并延长,过点A作AD⊥CE,垂足为D.已知AD=7,AB=20,BC=15,DC=24.
(1) 求证:∠B为直角;
(2) 记△ADE的面积为S1,△BCE的面积为S2,则S2-S1的值为 .
11 (2025扬州高邮期中)如图,在△ABC中,∠B=90°,AB=16 cm,BC=12 cm,M,N是△ABC边上的两个动点,其中点N从点A开始沿A→B方向运动,且速度为2 cm/s,点M从点B开始沿B→C→A方向运动,且速度为4 cm/s,它们同时出发,设运动的时间为t s.
(1) 出发2 s后,求MN的长;
(2) 当点M在边BC上运动时,出发几秒后,△MNB是等腰三角形?
(3) 当点M在边CA上运动时,求能使△BCM成为等腰三角形的t的值.
3.3 勾股定理的简单应用
第1课时 勾股定理在实际生活中的应用
1. A 2. C 3. 3 4. 50
5. 解:设AC=x m,则AE=AC=x m,AB=AE-BE=(x-1)m,
由题意,得∠ABC=90°,
在Rt△ABC中,由AB2+BC2=AC2,得(x-1)2+42=x2,
解得x=8.5,
所以滑道AC的长为8.5 m.
6. 解:设此时梯子底端B与右墙角点E的距离为x m,则BC=(2.2-x)m.
由题意可知AC=2.4 m,DE=2 m,AB=DB,
在Rt△ABC和Rt△DBE中,由勾股定理,得AB2=BC2+AC2,DB2=BE2+DE2,
所以BC2+AC2=BE2+DE2,
即(2.2-x)2+2.42=x2+4,
解得x=1.5,
故此时梯子底端B与右墙角点E的距离为1.5 m.
7. B 8. 15 9. 101
10. 解:(1) 在Rt△MNB中,由BN2=BM2-MN2,得BN=90(m),
所以AN=AB-BN=250-90=160(m).
在Rt△AMN中,由AM2=AN2+MN2,得AM=200(m),
所以供水点M到喷泉A,B需要铺设的管道总长=200+150=350(m).
(2) 因为AB=250 m,AM=200 m,BM=150 m,
所以AB2=BM2+AM2,
所以△ABM是直角三角形,且BM⊥AC,
所以喷泉B到小路AC的最短距离是BM=150 m.
11. 解:(1) 海港C受台风影响.理由如下:
如图,过点C作CD⊥AB于点D.
因为AC=300 km,BC=400 km,AB=500 km,
所以AC2+BC2=AB2,
所以△ABC是直角三角形,
所以S△ABC=×AC×BC=×CD×AB,
即300×400=500×CD,
所以CD==240(km),
因为以台风中心为圆心,周围250 km以内为受影响区域,
所以海港C受台风影响.
(2) 当EC=250 km,FC=250 km时,正好影响C海港,
因为ED==70(km),
所以EF=140 km.
因为台风中心移动的速度为20 km/h,
所以140÷20=7(h),
即台风影响海港C的持续时间为7 h.
第2课时 勾股定理在几何图形中的应用
1. B 2. A 3. 3.5 4.
5. 解:在数轴上画出点B表示3,作AB垂直于x轴,截取AB=1,根据勾股定理,得OA==,在数轴上用圆规截取OM=OA,点M表示的数就是.
6. 解:(1) EF⊥AC.理由如下:
连接AE,CE.
因为∠BAD=90°,E为边BD的中点,
所以AE=BD.
因为∠DCB=90°,E为边BD的中点,
所以CE=BD,
所以AE=CE.
因为F是AC的中点,
所以EF⊥AC.
(2) 因为AC=8,BD=10,E,F分别是边BD,AC的中点,
所以AE=CE=5,CF=4.
因为EF⊥AC,
所以EF===3.
7. C 8. 16 9.
10. (1) 证明:因为AD⊥CE,
所以∠D=90°.
因为AD=7,DC=24,
所以AC2=AD2+DC2=625=252.
因为AB=20,BC=15,202+152=252,
所以AB2+BC2=AC2,
所以△ABC是直角三角形,且∠B为直角.
(2) 66
11. 解:(1) 当t=2时,AN=2t=4 cm,BM=4t=8 cm.
因为AB=16 cm,
所以BN=AB-AN=16-4=12(cm).
在Rt△MNB中,由勾股定理可得
MN===(cm),
即MN的长为 cm.
(2) 由题意可知AN=2t cm,BM=4t cm,
又因为AB=16 cm,
所以BN=AB-AN=(16-2t)cm.
当△MNB为等腰三角形时,有BM=BN,
所以16-2t=4t,解得t=,
所以出发 s后△MNB是等腰三角形.
(3) 在△ABC中,由勾股定理可求得AC=20 cm,
当点M在AC上运动时,CM=(4t-12)cm.
因为△BCM为等腰三角形,
所以有BM=BC,CM=BC和CM=BM三种情况:
①当BM=BC=12 cm时,如图,过点B作BE⊥AC,
则CE=CM=2t-6.
在Rt△ABC中,由S△ABC=AB·BC=BE·AC,
得BE==9.6.
在Rt△BCE中,由勾股定理可得BC2=BE2+CE2,
即122=(9.6)2+(2t-6)2,
即(2t-6)2=7.22,
即2t-6=7.2或2t-6=-7.2,
解得t=6.6或t=-0.6(舍去).
②当CM=BC=12 cm时,则4t-12=12,解得t=6.
③当CM=BM时,即∠C=∠MBC,
因为∠C+∠A=90°=∠CBM+∠MBA,
所以∠A=∠MBA,
所以MB=MA,所以CM=AM=10 cm,
即4t-12=10,解得t=5.5.
综上,当t的值为6.6或6或5.5时,△BCM为等腰三角形.
同课章节目录
