4.2 图形变换与坐标变化 同步练(含答案) 2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 4.2 图形变换与坐标变化 同步练(含答案) 2025-2026学年数学苏科版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 432.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 15:32:33 | ||
图片预览


文档简介
4.2 图形变换与坐标变化
第1课时 平移与坐标变化
掌握图形在平移过程中坐标变化的规律(横坐标,右移加,左移减;纵坐标,上移加,下移减).
建议用时:15分钟
1 (2024海南)在平面直角坐标系中,将点A向右平移3个单位长度得到点A′(2,1),则点A的坐标是( )
A. (5,1) B. (2,4) C. (-1,1) D. (2,-2)
2 (2024南通通州月考)在平面直角坐标系中,将三角形各顶点的纵坐标都减去5,横坐标保持不变,所得图形与原图形相比( )
A. 向上平移了5个单位长度 B. 向下平移了5个单位长度
C. 向左平移了5个单位长度 D. 向右平移了5个单位长度
3 (2024江西)在平面直角坐标系中,将点A(1,1)向右平移2个单位长度,再向上平移3个单位长度得到点B,则点B的坐标为 .
4 (2025宿迁宿城一模)将点P(m,m+4)向上平移2个单位长度得到点Q,且点Q在x轴上,则点P的坐标为 .
5 如图,在平面直角坐标系中,平移△ABC至△A1B1C1的位置.若顶点A(-3,4)的对应点是A1(2,5),则点B(-4,2)的对应点B1的坐标是 .
(第5题) (第6题)
6 (2024淄博)如图,已知A,B两点的坐标分别为A(-3,1),B(-1,3),将线段AB平移得到线段CD.若点A的对应点是C(1,2),则点B的对应点D的坐标是 .
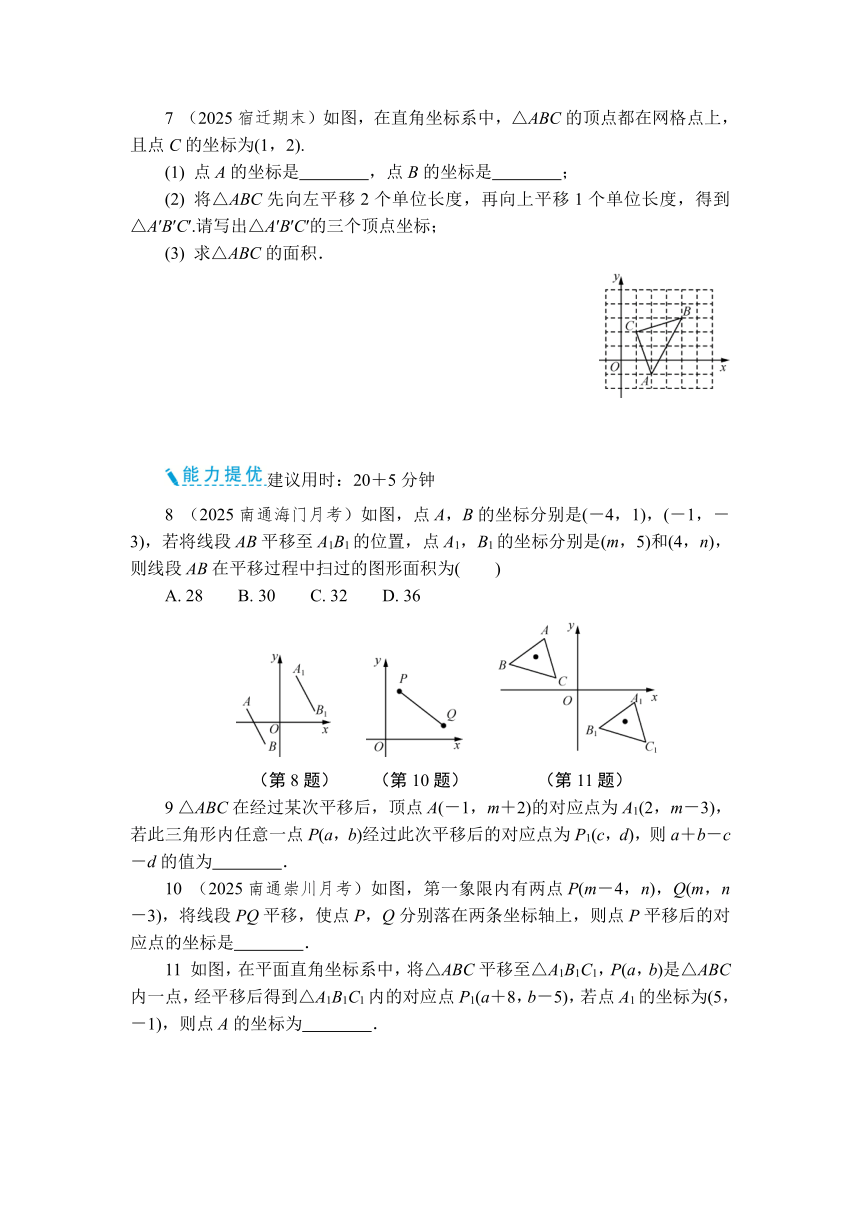
7 (2025宿迁期末)如图,在直角坐标系中,△ABC的顶点都在网格点上,且点C的坐标为(1,2).
(1) 点A的坐标是 ,点B的坐标是 ;
(2) 将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′.请写出△A′B′C′的三个顶点坐标;
(3) 求△ABC的面积.
建议用时:20+5分钟
8 (2025南通海门月考)如图,点A,B的坐标分别是(-4,1),(-1,-3),若将线段AB平移至A1B1的位置,点A1,B1的坐标分别是(m,5)和(4,n),则线段AB在平移过程中扫过的图形面积为( )
A. 28 B. 30 C. 32 D. 36
(第8题) (第10题) (第11题)
9 △ABC在经过某次平移后,顶点A(-1,m+2)的对应点为A1(2,m-3),若此三角形内任意一点P(a,b)经过此次平移后的对应点为P1(c,d),则a+b-c-d的值为 .
10 (2025南通崇川月考)如图,第一象限内有两点P(m-4,n),Q(m,n-3),将线段PQ平移,使点P,Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是 .
11 如图,在平面直角坐标系中,将△ABC平移至△A1B1C1,P(a,b)是△ABC内一点,经平移后得到△A1B1C1内的对应点P1(a+8,b-5),若点A1的坐标为(5,-1),则点A的坐标为 .
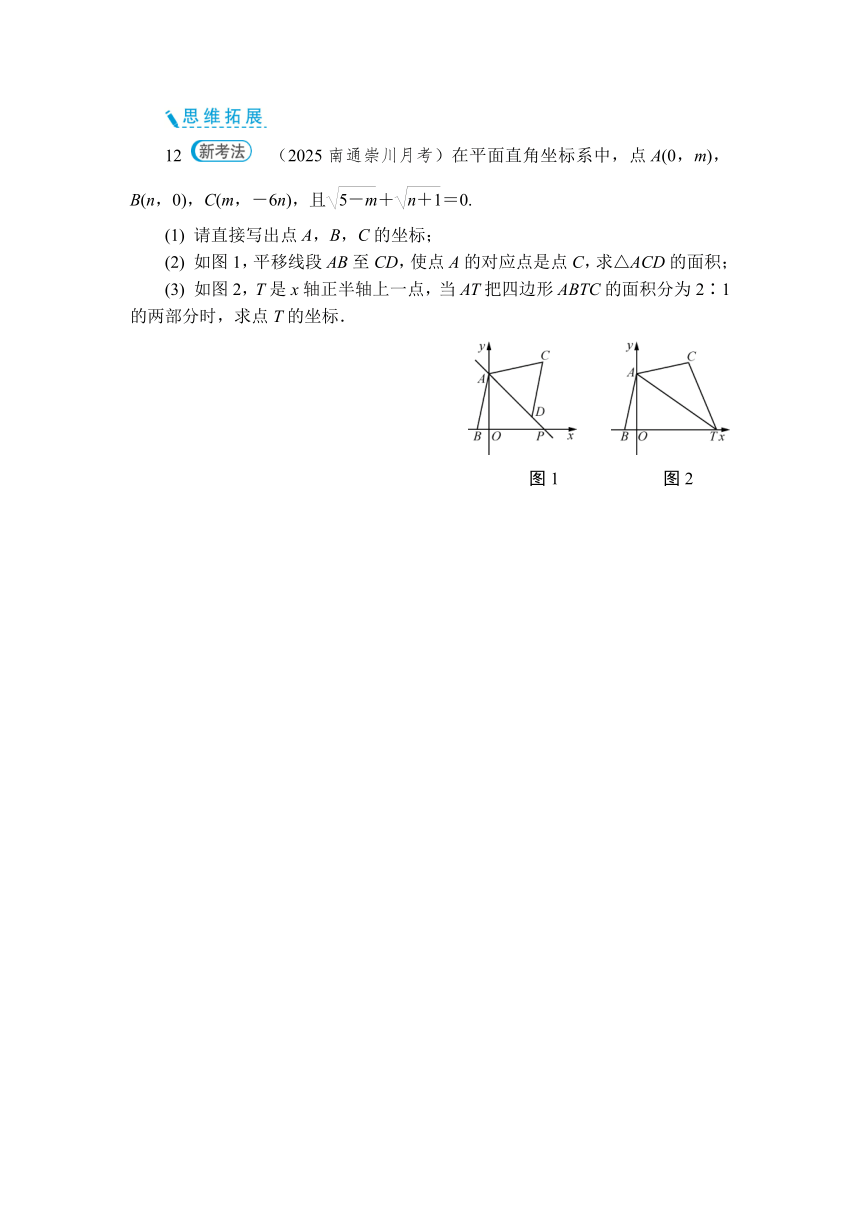
12 (2025南通崇川月考)在平面直角坐标系中,点A(0,m),B(n,0),C(m,-6n),且+=0.
(1) 请直接写出点A,B,C的坐标;
(2) 如图1,平移线段AB至CD,使点A的对应点是点C,求△ACD的面积;
(3) 如图2,T是x轴正半轴上一点,当AT把四边形ABTC的面积分为2∶1的两部分时,求点T的坐标.
图1 图2
第2课时 轴对称与坐标变化
掌握图形关于x轴,y轴,原点对称的坐标变化规律.
建议用时:15分钟
1 (2024绵阳)蝴蝶颜色绚丽,翩翩起舞时非常美丽,深受人们喜爱,它的图案具有对称美.如图,蝴蝶图案关于y轴对称,点M的对应点为M1,若点M的坐标为(-2,-3),则点M1的坐标为( )
A. (2,-3) B. (-3,2) C. (-2,3) D. (2,3)
2 (2025无锡期末)若点P(m,1)与点Q(3,-1)关于x轴对称,则m的值为( )
A. 3 B. -3 C. 1 D. -1
3 (2025苏州模拟)在平面直角坐标系中,点A(3,-2),B(m,n)关于x轴对称,将点B向左平移3个单位长度得到点C,则点C的坐标为( )
A. (3,-2) B. (3,2) C. (0,-2) D. (0,2)
4 (2024扬州)在平面直角坐标系中,点P(1,2)关于坐标原点的对称点P′的坐标为( )
A. (-1,-2) B. (-1,2) C. (1,-2) D. (1,2)
5 (2025盐城建湖一模)在平面直角坐标系中,作点P(1,-3)关于y轴的对称点P1,再将点P1向左平移3个单位长度,得到点P2,则点P2的坐标为 W.
6 在平面直角坐标系中,点P(3m-1,2-m)与点P′关于原点对称,且点P′在第三象限,则m的取值范围是 .
7 (2025常州金坛一模)如图,在平面直角坐标系中,点D的坐标为(4,-2),DC⊥x轴,垂足为C,将Rt△OCD绕点O按逆时针方向旋转90°得到△OAB,则点B的坐标是 .
8 (教材P123例2变式)在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(3,4),C(3,-1).
(1) 试在平面直角坐标系中,标出A,B,C三点,并依次连接;
(2) 求△ABC的面积;
(3) 若△A1B1C1与△ABC关于x轴对称,请写出A1,B1,C1三点的坐标.
建议用时:20+5分钟
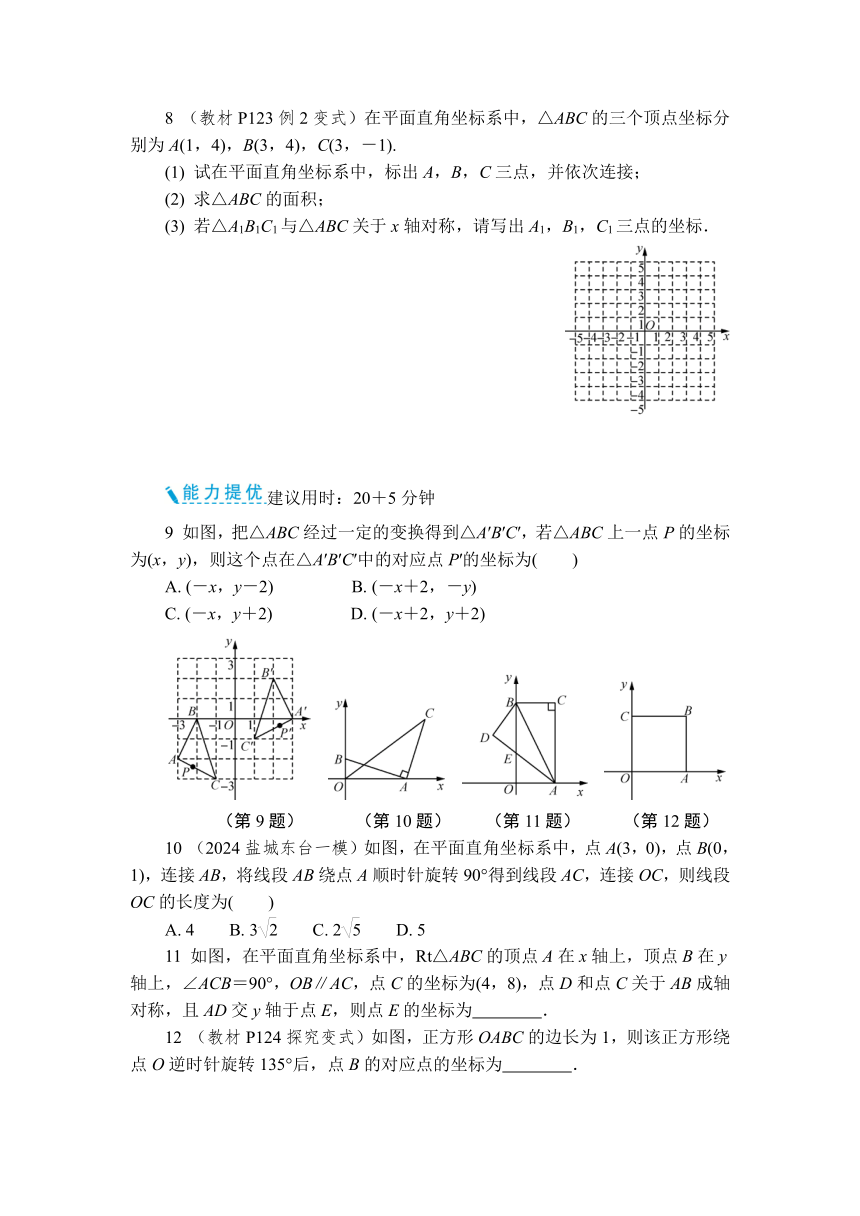
9 如图,把△ABC经过一定的变换得到△A′B′C′,若△ABC上一点P的坐标为(x,y),则这个点在△A′B′C′中的对应点P′的坐标为( )
A. (-x,y-2) B. (-x+2,-y)
C. (-x,y+2) D. (-x+2,y+2)
(第9题) (第10题) (第11题) (第12题)
10 (2024盐城东台一模)如图,在平面直角坐标系中,点A(3,0),点B(0,1),连接AB,将线段AB绕点A顺时针旋转90°得到线段AC,连接OC,则线段OC的长度为( )
A. 4 B. 3 C. 2 D. 5
11 如图,在平面直角坐标系中,Rt△ABC的顶点A在x轴上,顶点B在y轴上,∠ACB=90°,OB∥AC,点C的坐标为(4,8),点D和点C关于AB成轴对称,且AD交y轴于点E,则点E的坐标为 .
12 (教材P124探究变式)如图,正方形OABC的边长为1,则该正方形绕点O逆时针旋转135°后,点B的对应点的坐标为 .
13 阅读材料并解答下列问题:如图,把平面内一条数轴x绕原点O逆时针旋转角θ(0°<θ<90°)得到另一条数轴y,x轴和y轴构成一个平面斜坐标系xOy.规定:过点P作y轴的平行线,交x轴于点A,过点P作x轴的平行线,交y轴于点B,若点A在x轴对应的实数为a,点B在y轴对应的实数为b,则称有序实数对(a,b)为点P在平面斜坐标系xOy中的斜坐标.如图,在平面斜坐标系xOy中,已知θ=60°,点P的斜坐标是(3,6).
(1) 连接OP,求线段OP的长;
(2) 将线段OP绕点O顺时针旋转60°到OQ(点Q与点P对应),求点Q的斜坐标.
第3课时 特殊线上点的特征
掌握平面直角坐标系中特殊线上点的特征.
建议用时:15分钟
1 (2025泰州靖江期末)已知直线MN∥x轴,点M的坐标为(2,3),并且线段MN=3,则点N的坐标为( )
A. (-1,3) B. (5,3) C. (1,3)或(5,3) D. (-1,3)或(5,3)
2 (2025连云港期末)如图,在平面直角坐标系中,直线l1过点(3,0)且平行于y轴,直线l2过点(0,-4)且平行于x轴,点P的坐标为(a,b).根据图中点P的位置,下列结论中正确的是( )
A. a<-4,b>3 B. 0<a<3,b<3
C. a>3,b<-4 D. a>3,-4<b<0
(第2题) (第3题)
3 (2025无锡锡山期末)如图,在平面直角坐标系中,点B的坐标是(8,12),点C的坐标是(8,2),AB=AC=13,则点A的坐标是( )
A. (3,6) B. (-4,5) C. (-4,6) D. (-4,7)
4 (2025南通如皋月考)若点P(2a,1-3a)在第二象限,且点P到x轴的距离与到y轴的距离之和是11,则a的值为 .
5 (2025泰州海陵期末)已知AB∥y轴,且点A的坐标为(m,2m-1),点B的坐标为(2,4),则点A的坐标为 .
6 在平面直角坐标系中,点A(2,3)与点B(-2,3)是一个轴对称图形上对称的两点,该图形只有一条对称轴,则图形中与点C(4,-1)成轴对称的点D的坐标是 .
7 已知点P(a,2a-1)在第一、三象限的角平分线上,则a的值为 .
8 (2025南通海安月考)已知点P(3a-4,a+2).
(1) 若点P在y轴上,求出点P的坐标;
(2) 若点Q的坐标为(2,5),直线PQ∥y轴,求出点P的坐标;
(3) 若点P到x轴,y轴的距离相等,求出点P的坐标.
9 如图,将点P(-1,2)关于第一、三象限的角平分线l对称,得到点P′,则点P′的坐标为( )
A. (2,1) B. (2,-1) C. (1,-2) D. (-1,-2)
(第9题) (第10题) (第11题) (第12题)
10 如图,从点M(0,3)发出一束光,经x轴反射,过点N(6,5),则这束光从点M到点N所经过的路径的长为( )
A. 8 B. 9 C. 10 D. 12.5
11 (2025连云港灌云月考)如图,点A,B分别在x轴,y轴上,OA=OB,分别以点A,B为圆心,以大于AB长为半径画弧,两弧交于点P.若点P的坐标为(2a,3a-4),则a的值为 .
12 (2025无锡梁溪月考)如图,过点A的直线l∥x轴,点B在x轴的正半轴上,OC平分∠AOB交直线l于点C(2,4),则点A的坐标是 .
13 在平面直角坐标系中,点A(a,b),B(2,2),且|a-b+8|+=0.
(1) 求点A的坐标;
(2) 过点A作AC⊥x轴于点C,连接BC,AB,求△ABC的面积;
(3) 在(2)的条件下,延长AB交 x轴于点D,AB交y轴于点E,则OD与OE是否相等?请说明理由.
14 (2025宿迁宿城期末)在平面直角坐标系中,已知点M的坐标为(2-t,2t),将点M到x轴的距离记作d1,到y轴的距离记作d2.
(1) 若t=3,则d1+d2= ;
(2) 若t<0,d1=d2,求点M的坐标;
(3) 若点M在第二象限,且md1-5d2=10(m为常数),求m的值.
4.2 图形变换与坐标变化
第1课时 平移与坐标变化
1. C 2. B 3. (3,4) 4. (-6,-2) 5. (1,3) 6. (3,4)
7. 解:(1) (2,-1) (4,3)
(2) △A′B′C′的三个顶点坐标分别为A′(0,0),B′(2,4),C′(-1,3).
(3) S△ABC=3×4-×2×4-×3×1-×3×1=5.
8. C 9. 2 10. (0,3)或(-4,0) 11. (-3,4)
12. 解:(1) 因为+=0,
所以5-m=0,n+1=0,
所以m=5,n=-1,
所以A(0,5),B(-1,0),C(5,6).
(2) 因为平移线段AB至CD,使点A的对应点是点C,点A(0,5),C(5,6),
所以平移方式为向右移动5个单位长度,向上移动1个单位长度.
又点B(-1,0),所以点D的坐标为(-1+5,0+1),即(4,1).
如图1,过点C和点D分别作y轴的垂线,垂足分别为G,H,则CG=5,DH=4,AH=4,AG=1,
所以S△ACD=S梯形CGHD-S△ACG-S△ADH=×5-×4×4-×5×1 =12.
(3) 如图2,连接OC,设点T(t,0)(t>0).
因为A(0,5),B(-1,0),C(5,6),
所以S四边形ABTC=S△ABO+S△AOC+S△COT=×1×5+×5×5+×6t =15+3t.
当S△ABT∶S△ACT=1∶2时,S△ABT=S四边形ABTC,
所以×5(t+1)=(15+3t),
解得t=,所以T(,0);
当S△ABT∶S△ACT=2∶1时,S△ABT=S四边形ABTC,
所以×5(t+1)=(15+3t),
解得t=15,所以T(15,0).
综上,当AT把四边形ABTC的面积分为2∶1的两部分时,点T的坐标为(,0)或(15,0).
图1 图2
第2课时 轴对称与坐标变化
1. A 2. A 3. D 4. A 5. (-4,-3) 6. <m<2
7. (2,4)
8. 解:(1) 如图,点A,B,C即为所求.
(2) △ABC的面积为×(3-1)×(4+1)=5.
(3) 若△A1B1C1与△ABC关于x轴对称,则点A1(1,-4),B1(3,-4),C1(3,1).
9. C 10. D 11. (0,3) 12. (-,0)
13. 解:(1) 如图1,过点P作PC⊥OA,垂足为C,连接OP.
因为AP∥OB,
所以∠PAC=θ=60°,则∠APC=30°,
所以AC=AP.
因为点P的斜坐标是(3,6),
所以OA=3,OB=AP=6,
所以AC=AP=3,
所以PC==,OC=3+3=6,
在Rt△OCP中,由勾股定理,得OP==.
(2) 如图2,过点P作PC⊥OA,垂足为C,过点Q作QE∥OB,QF∥OC,连接CQ.
由旋转的性质,得OP=OQ,∠POQ=60°.
因为∠BOP+∠POA=∠POA+∠COQ=60°,
所以∠BOP=∠COQ.
在△BOP和△COQ中,
所以△BOP≌△COQ(SAS),
所以BP=CQ=3,∠OBP=∠OCQ=120°,
所以∠ECQ=60°.
因为EQ∥OB,
所以∠CEQ=60°,
所以△CEQ是等边三角形,
所以CE=EQ=CQ=3,
所以OE=6+3=9,OF=EQ=3,
所以点Q的斜坐标为(9,-3).
图1 图2
第3课时 特殊线上点的特征
1. D 2. D 3. D 4. -2 5. (2,3) 6. (-4,-1) 7. 1
8. 解:(1) 由题意,得3a-4=0,
解得a=,所以a+2=,
所以点P的坐标为(0,).
(2) 由题意,得3a-4=2,
解得a=2,所以a+2=4,
所以点P的坐标为(2,4).
(3) 由题意,得|3a-4|=|a+2|,
解得a=3或a=,
当a=3时,3a-4=5,a+2=5,P(5,5);
当a=时,3a-4=-,a+2=,P(-,),
所以点P的坐标为(5,5)或(-,).
9. B 10. C 11. 4 12. (-3,4)
13. 解:(1) 由|a-b+8|+=0,
得解得
所以点A的坐标为(-2,6).
(2) 如图1,过点B作BF⊥x轴于点F,
则S△ABC=S梯形ACFB-S△BCF=×(2+6)×4-×4×2=12.
(3) OD与OE相等.理由如下:
如图2,设点D的坐标为(x,0)(x>0),点E的坐标为(0,y)(y>0),
则CD=x+2,OE=y.
因为S△ABC=S△ACD-S△BCD ,
所以12=×(x+2)×6-×(x+2)×2=2(x+2),
解得x=4,即OD=4.
又因为S△EOD=S△ACD-S梯形ACOE ,
所以×4×y=×6×6-×(y+6)×2,
解得y=4,即OE=4,
所以OD=OE.
图1 图2
14. 解:(1) 7
(2) 由题意,得d1=|2t|,d2=|2-t|.
因为t<0,
所以2-t>0,2t<0,
所以d1=|2t|=-2t,d2=|2-t|=2-t,
因为d1=d2,
所以-2t=2-t,
解得t=-2,
所以2-t=2-(-2)=4,2t=2×(-2)=-4,
所以点M的坐标为(4,-4).
(3) 因为点M在第二象限,
所以2-t<0,2t>0,
所以d1=|2t|=2t,d2=|2-t|=t-2.
因为md1-5d2=10,
所以m×2t-5×(t-2)=10,
解得m=.
第1课时 平移与坐标变化
掌握图形在平移过程中坐标变化的规律(横坐标,右移加,左移减;纵坐标,上移加,下移减).
建议用时:15分钟
1 (2024海南)在平面直角坐标系中,将点A向右平移3个单位长度得到点A′(2,1),则点A的坐标是( )
A. (5,1) B. (2,4) C. (-1,1) D. (2,-2)
2 (2024南通通州月考)在平面直角坐标系中,将三角形各顶点的纵坐标都减去5,横坐标保持不变,所得图形与原图形相比( )
A. 向上平移了5个单位长度 B. 向下平移了5个单位长度
C. 向左平移了5个单位长度 D. 向右平移了5个单位长度
3 (2024江西)在平面直角坐标系中,将点A(1,1)向右平移2个单位长度,再向上平移3个单位长度得到点B,则点B的坐标为 .
4 (2025宿迁宿城一模)将点P(m,m+4)向上平移2个单位长度得到点Q,且点Q在x轴上,则点P的坐标为 .
5 如图,在平面直角坐标系中,平移△ABC至△A1B1C1的位置.若顶点A(-3,4)的对应点是A1(2,5),则点B(-4,2)的对应点B1的坐标是 .
(第5题) (第6题)
6 (2024淄博)如图,已知A,B两点的坐标分别为A(-3,1),B(-1,3),将线段AB平移得到线段CD.若点A的对应点是C(1,2),则点B的对应点D的坐标是 .
7 (2025宿迁期末)如图,在直角坐标系中,△ABC的顶点都在网格点上,且点C的坐标为(1,2).
(1) 点A的坐标是 ,点B的坐标是 ;
(2) 将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′.请写出△A′B′C′的三个顶点坐标;
(3) 求△ABC的面积.
建议用时:20+5分钟
8 (2025南通海门月考)如图,点A,B的坐标分别是(-4,1),(-1,-3),若将线段AB平移至A1B1的位置,点A1,B1的坐标分别是(m,5)和(4,n),则线段AB在平移过程中扫过的图形面积为( )
A. 28 B. 30 C. 32 D. 36
(第8题) (第10题) (第11题)
9 △ABC在经过某次平移后,顶点A(-1,m+2)的对应点为A1(2,m-3),若此三角形内任意一点P(a,b)经过此次平移后的对应点为P1(c,d),则a+b-c-d的值为 .
10 (2025南通崇川月考)如图,第一象限内有两点P(m-4,n),Q(m,n-3),将线段PQ平移,使点P,Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是 .
11 如图,在平面直角坐标系中,将△ABC平移至△A1B1C1,P(a,b)是△ABC内一点,经平移后得到△A1B1C1内的对应点P1(a+8,b-5),若点A1的坐标为(5,-1),则点A的坐标为 .
12 (2025南通崇川月考)在平面直角坐标系中,点A(0,m),B(n,0),C(m,-6n),且+=0.
(1) 请直接写出点A,B,C的坐标;
(2) 如图1,平移线段AB至CD,使点A的对应点是点C,求△ACD的面积;
(3) 如图2,T是x轴正半轴上一点,当AT把四边形ABTC的面积分为2∶1的两部分时,求点T的坐标.
图1 图2
第2课时 轴对称与坐标变化
掌握图形关于x轴,y轴,原点对称的坐标变化规律.
建议用时:15分钟
1 (2024绵阳)蝴蝶颜色绚丽,翩翩起舞时非常美丽,深受人们喜爱,它的图案具有对称美.如图,蝴蝶图案关于y轴对称,点M的对应点为M1,若点M的坐标为(-2,-3),则点M1的坐标为( )
A. (2,-3) B. (-3,2) C. (-2,3) D. (2,3)
2 (2025无锡期末)若点P(m,1)与点Q(3,-1)关于x轴对称,则m的值为( )
A. 3 B. -3 C. 1 D. -1
3 (2025苏州模拟)在平面直角坐标系中,点A(3,-2),B(m,n)关于x轴对称,将点B向左平移3个单位长度得到点C,则点C的坐标为( )
A. (3,-2) B. (3,2) C. (0,-2) D. (0,2)
4 (2024扬州)在平面直角坐标系中,点P(1,2)关于坐标原点的对称点P′的坐标为( )
A. (-1,-2) B. (-1,2) C. (1,-2) D. (1,2)
5 (2025盐城建湖一模)在平面直角坐标系中,作点P(1,-3)关于y轴的对称点P1,再将点P1向左平移3个单位长度,得到点P2,则点P2的坐标为 W.
6 在平面直角坐标系中,点P(3m-1,2-m)与点P′关于原点对称,且点P′在第三象限,则m的取值范围是 .
7 (2025常州金坛一模)如图,在平面直角坐标系中,点D的坐标为(4,-2),DC⊥x轴,垂足为C,将Rt△OCD绕点O按逆时针方向旋转90°得到△OAB,则点B的坐标是 .
8 (教材P123例2变式)在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(3,4),C(3,-1).
(1) 试在平面直角坐标系中,标出A,B,C三点,并依次连接;
(2) 求△ABC的面积;
(3) 若△A1B1C1与△ABC关于x轴对称,请写出A1,B1,C1三点的坐标.
建议用时:20+5分钟
9 如图,把△ABC经过一定的变换得到△A′B′C′,若△ABC上一点P的坐标为(x,y),则这个点在△A′B′C′中的对应点P′的坐标为( )
A. (-x,y-2) B. (-x+2,-y)
C. (-x,y+2) D. (-x+2,y+2)
(第9题) (第10题) (第11题) (第12题)
10 (2024盐城东台一模)如图,在平面直角坐标系中,点A(3,0),点B(0,1),连接AB,将线段AB绕点A顺时针旋转90°得到线段AC,连接OC,则线段OC的长度为( )
A. 4 B. 3 C. 2 D. 5
11 如图,在平面直角坐标系中,Rt△ABC的顶点A在x轴上,顶点B在y轴上,∠ACB=90°,OB∥AC,点C的坐标为(4,8),点D和点C关于AB成轴对称,且AD交y轴于点E,则点E的坐标为 .
12 (教材P124探究变式)如图,正方形OABC的边长为1,则该正方形绕点O逆时针旋转135°后,点B的对应点的坐标为 .
13 阅读材料并解答下列问题:如图,把平面内一条数轴x绕原点O逆时针旋转角θ(0°<θ<90°)得到另一条数轴y,x轴和y轴构成一个平面斜坐标系xOy.规定:过点P作y轴的平行线,交x轴于点A,过点P作x轴的平行线,交y轴于点B,若点A在x轴对应的实数为a,点B在y轴对应的实数为b,则称有序实数对(a,b)为点P在平面斜坐标系xOy中的斜坐标.如图,在平面斜坐标系xOy中,已知θ=60°,点P的斜坐标是(3,6).
(1) 连接OP,求线段OP的长;
(2) 将线段OP绕点O顺时针旋转60°到OQ(点Q与点P对应),求点Q的斜坐标.
第3课时 特殊线上点的特征
掌握平面直角坐标系中特殊线上点的特征.
建议用时:15分钟
1 (2025泰州靖江期末)已知直线MN∥x轴,点M的坐标为(2,3),并且线段MN=3,则点N的坐标为( )
A. (-1,3) B. (5,3) C. (1,3)或(5,3) D. (-1,3)或(5,3)
2 (2025连云港期末)如图,在平面直角坐标系中,直线l1过点(3,0)且平行于y轴,直线l2过点(0,-4)且平行于x轴,点P的坐标为(a,b).根据图中点P的位置,下列结论中正确的是( )
A. a<-4,b>3 B. 0<a<3,b<3
C. a>3,b<-4 D. a>3,-4<b<0
(第2题) (第3题)
3 (2025无锡锡山期末)如图,在平面直角坐标系中,点B的坐标是(8,12),点C的坐标是(8,2),AB=AC=13,则点A的坐标是( )
A. (3,6) B. (-4,5) C. (-4,6) D. (-4,7)
4 (2025南通如皋月考)若点P(2a,1-3a)在第二象限,且点P到x轴的距离与到y轴的距离之和是11,则a的值为 .
5 (2025泰州海陵期末)已知AB∥y轴,且点A的坐标为(m,2m-1),点B的坐标为(2,4),则点A的坐标为 .
6 在平面直角坐标系中,点A(2,3)与点B(-2,3)是一个轴对称图形上对称的两点,该图形只有一条对称轴,则图形中与点C(4,-1)成轴对称的点D的坐标是 .
7 已知点P(a,2a-1)在第一、三象限的角平分线上,则a的值为 .
8 (2025南通海安月考)已知点P(3a-4,a+2).
(1) 若点P在y轴上,求出点P的坐标;
(2) 若点Q的坐标为(2,5),直线PQ∥y轴,求出点P的坐标;
(3) 若点P到x轴,y轴的距离相等,求出点P的坐标.
9 如图,将点P(-1,2)关于第一、三象限的角平分线l对称,得到点P′,则点P′的坐标为( )
A. (2,1) B. (2,-1) C. (1,-2) D. (-1,-2)
(第9题) (第10题) (第11题) (第12题)
10 如图,从点M(0,3)发出一束光,经x轴反射,过点N(6,5),则这束光从点M到点N所经过的路径的长为( )
A. 8 B. 9 C. 10 D. 12.5
11 (2025连云港灌云月考)如图,点A,B分别在x轴,y轴上,OA=OB,分别以点A,B为圆心,以大于AB长为半径画弧,两弧交于点P.若点P的坐标为(2a,3a-4),则a的值为 .
12 (2025无锡梁溪月考)如图,过点A的直线l∥x轴,点B在x轴的正半轴上,OC平分∠AOB交直线l于点C(2,4),则点A的坐标是 .
13 在平面直角坐标系中,点A(a,b),B(2,2),且|a-b+8|+=0.
(1) 求点A的坐标;
(2) 过点A作AC⊥x轴于点C,连接BC,AB,求△ABC的面积;
(3) 在(2)的条件下,延长AB交 x轴于点D,AB交y轴于点E,则OD与OE是否相等?请说明理由.
14 (2025宿迁宿城期末)在平面直角坐标系中,已知点M的坐标为(2-t,2t),将点M到x轴的距离记作d1,到y轴的距离记作d2.
(1) 若t=3,则d1+d2= ;
(2) 若t<0,d1=d2,求点M的坐标;
(3) 若点M在第二象限,且md1-5d2=10(m为常数),求m的值.
4.2 图形变换与坐标变化
第1课时 平移与坐标变化
1. C 2. B 3. (3,4) 4. (-6,-2) 5. (1,3) 6. (3,4)
7. 解:(1) (2,-1) (4,3)
(2) △A′B′C′的三个顶点坐标分别为A′(0,0),B′(2,4),C′(-1,3).
(3) S△ABC=3×4-×2×4-×3×1-×3×1=5.
8. C 9. 2 10. (0,3)或(-4,0) 11. (-3,4)
12. 解:(1) 因为+=0,
所以5-m=0,n+1=0,
所以m=5,n=-1,
所以A(0,5),B(-1,0),C(5,6).
(2) 因为平移线段AB至CD,使点A的对应点是点C,点A(0,5),C(5,6),
所以平移方式为向右移动5个单位长度,向上移动1个单位长度.
又点B(-1,0),所以点D的坐标为(-1+5,0+1),即(4,1).
如图1,过点C和点D分别作y轴的垂线,垂足分别为G,H,则CG=5,DH=4,AH=4,AG=1,
所以S△ACD=S梯形CGHD-S△ACG-S△ADH=×5-×4×4-×5×1 =12.
(3) 如图2,连接OC,设点T(t,0)(t>0).
因为A(0,5),B(-1,0),C(5,6),
所以S四边形ABTC=S△ABO+S△AOC+S△COT=×1×5+×5×5+×6t =15+3t.
当S△ABT∶S△ACT=1∶2时,S△ABT=S四边形ABTC,
所以×5(t+1)=(15+3t),
解得t=,所以T(,0);
当S△ABT∶S△ACT=2∶1时,S△ABT=S四边形ABTC,
所以×5(t+1)=(15+3t),
解得t=15,所以T(15,0).
综上,当AT把四边形ABTC的面积分为2∶1的两部分时,点T的坐标为(,0)或(15,0).
图1 图2
第2课时 轴对称与坐标变化
1. A 2. A 3. D 4. A 5. (-4,-3) 6. <m<2
7. (2,4)
8. 解:(1) 如图,点A,B,C即为所求.
(2) △ABC的面积为×(3-1)×(4+1)=5.
(3) 若△A1B1C1与△ABC关于x轴对称,则点A1(1,-4),B1(3,-4),C1(3,1).
9. C 10. D 11. (0,3) 12. (-,0)
13. 解:(1) 如图1,过点P作PC⊥OA,垂足为C,连接OP.
因为AP∥OB,
所以∠PAC=θ=60°,则∠APC=30°,
所以AC=AP.
因为点P的斜坐标是(3,6),
所以OA=3,OB=AP=6,
所以AC=AP=3,
所以PC==,OC=3+3=6,
在Rt△OCP中,由勾股定理,得OP==.
(2) 如图2,过点P作PC⊥OA,垂足为C,过点Q作QE∥OB,QF∥OC,连接CQ.
由旋转的性质,得OP=OQ,∠POQ=60°.
因为∠BOP+∠POA=∠POA+∠COQ=60°,
所以∠BOP=∠COQ.
在△BOP和△COQ中,
所以△BOP≌△COQ(SAS),
所以BP=CQ=3,∠OBP=∠OCQ=120°,
所以∠ECQ=60°.
因为EQ∥OB,
所以∠CEQ=60°,
所以△CEQ是等边三角形,
所以CE=EQ=CQ=3,
所以OE=6+3=9,OF=EQ=3,
所以点Q的斜坐标为(9,-3).
图1 图2
第3课时 特殊线上点的特征
1. D 2. D 3. D 4. -2 5. (2,3) 6. (-4,-1) 7. 1
8. 解:(1) 由题意,得3a-4=0,
解得a=,所以a+2=,
所以点P的坐标为(0,).
(2) 由题意,得3a-4=2,
解得a=2,所以a+2=4,
所以点P的坐标为(2,4).
(3) 由题意,得|3a-4|=|a+2|,
解得a=3或a=,
当a=3时,3a-4=5,a+2=5,P(5,5);
当a=时,3a-4=-,a+2=,P(-,),
所以点P的坐标为(5,5)或(-,).
9. B 10. C 11. 4 12. (-3,4)
13. 解:(1) 由|a-b+8|+=0,
得解得
所以点A的坐标为(-2,6).
(2) 如图1,过点B作BF⊥x轴于点F,
则S△ABC=S梯形ACFB-S△BCF=×(2+6)×4-×4×2=12.
(3) OD与OE相等.理由如下:
如图2,设点D的坐标为(x,0)(x>0),点E的坐标为(0,y)(y>0),
则CD=x+2,OE=y.
因为S△ABC=S△ACD-S△BCD ,
所以12=×(x+2)×6-×(x+2)×2=2(x+2),
解得x=4,即OD=4.
又因为S△EOD=S△ACD-S梯形ACOE ,
所以×4×y=×6×6-×(y+6)×2,
解得y=4,即OE=4,
所以OD=OE.
图1 图2
14. 解:(1) 7
(2) 由题意,得d1=|2t|,d2=|2-t|.
因为t<0,
所以2-t>0,2t<0,
所以d1=|2t|=-2t,d2=|2-t|=2-t,
因为d1=d2,
所以-2t=2-t,
解得t=-2,
所以2-t=2-(-2)=4,2t=2×(-2)=-4,
所以点M的坐标为(4,-4).
(3) 因为点M在第二象限,
所以2-t<0,2t>0,
所以d1=|2t|=2t,d2=|2-t|=t-2.
因为md1-5d2=10,
所以m×2t-5×(t-2)=10,
解得m=.
同课章节目录
