5.3 一次函数的图象与性质 同步练(含答案) 2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 5.3 一次函数的图象与性质 同步练(含答案) 2025-2026学年数学苏科版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 385.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 15:32:09 | ||
图片预览




文档简介
5.3 一次函数的图象与性质
第1课时 正比例函数的图象
会用描点法画正比例函数的图象,正比例函数的图象过原点.
建议用时:15分钟
1 (2025南通月考)若正比例函数的图象经过点(-5,6),则这个图象必经过( )
A. (5,-6) B. (-6,5) C. (5,6) D. (-5,-6)
2 正比例函数y=x的大致图象是( )
A B C D
3 已知A(-3,4),B(2,-3),C(3,-4),D(-5,)四个点,则与其他三个点不在同一正比例函数图象上的是( )
A. 点A B. 点B C. 点C D. 点D
4 (2024德阳)若正比例函数y=kx(k≠0)的图象如图所示,则k的值可能是( )
A. B. -
C. -1 D. -
5 若P(a,b)是正比例函数y=-x图象上任意一点,则下列等式中一定成立的是( )
A. 2a+3b=0 B. 2a-3b=0 C. 3a+2b=0 D. 3a-2b=0
6 画正比例函数y=2x的图象,比较简单的方法是过点 和 作一直线即可得到.
7 (2025无锡宜兴月考)如果点A(-3,-6),B(1,m)在同一正比例函数的图象上,那么m的值为 .
8 正比例函数y=-x的图象平分第 象限.
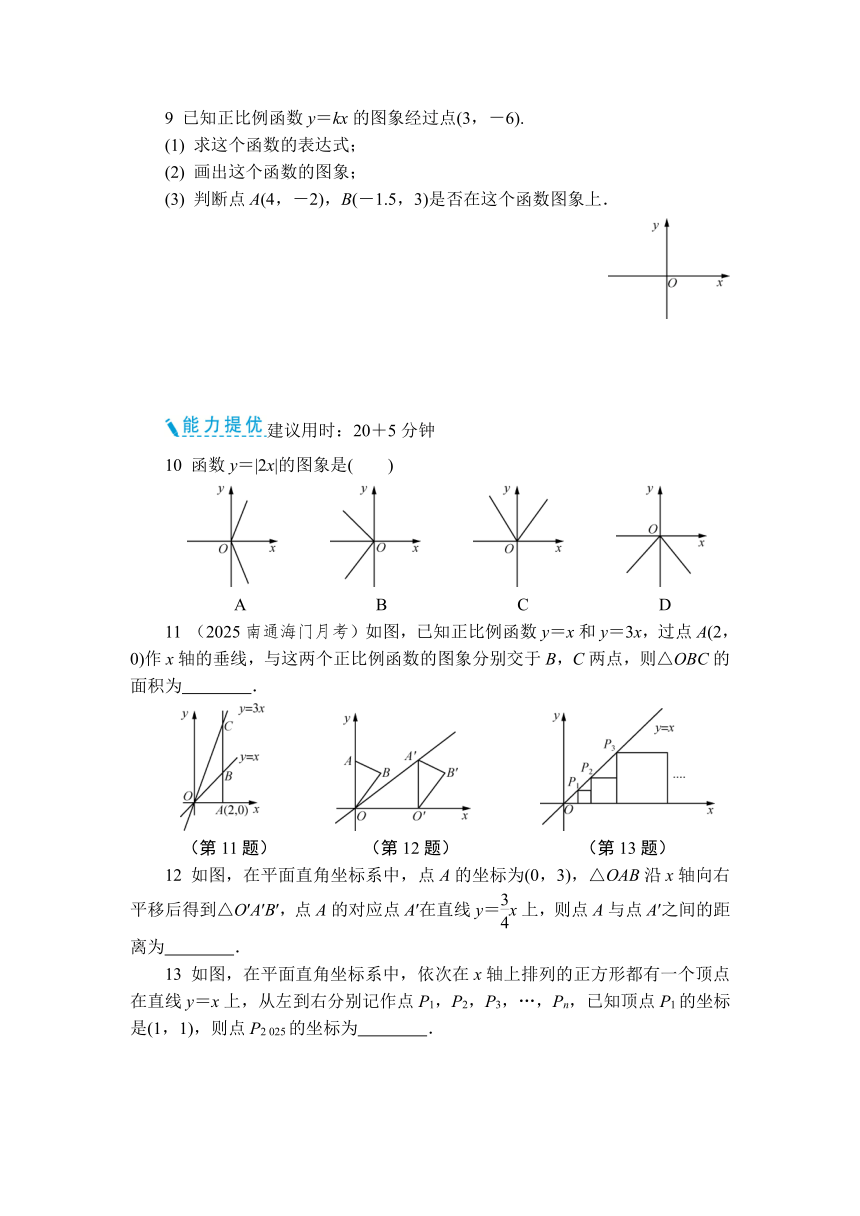
9 已知正比例函数y=kx的图象经过点(3,-6).
(1) 求这个函数的表达式;
(2) 画出这个函数的图象;
(3) 判断点A(4,-2),B(-1.5,3)是否在这个函数图象上.
建议用时:20+5分钟
10 函数y=|2x|的图象是( )
A B C D
11 (2025南通海门月考)如图,已知正比例函数y=x和y=3x,过点A(2,0)作x轴的垂线,与这两个正比例函数的图象分别交于B,C两点,则△OBC的面积为 .
(第11题) (第12题) (第13题)
12 如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A′在直线y=x上,则点A与点A′之间的距离为 .
13 如图,在平面直角坐标系中,依次在x轴上排列的正方形都有一个顶点在直线y=x上,从左到右分别记作点P1,P2,P3,…,Pn,已知顶点P1的坐标是(1,1),则点P2 025的坐标为 .
14 如图,点A(1,4)在正比例函数y=mx的图象上,点B(3,n)在正比例函数y=x的图象上.
(1) 求m,n的值;
(2) 在x轴上找一点P,使得PA+PB的值最小,请求出PA+PB的最小值.
15 如图,已知四边形ABCD是正方形,点B,C分别在两条直线y=2x和y=kx上,A,D是x轴上的两点.
(1) 若此正方形的边长为2,则k= ;
(2) 若此正方形的边长为a,k的值是否会发生变化?若不会发生变化,请说明理由;若会发生变化,求出a的值.
第2课时 正比例函数的性质
掌握正比例函数的图象特征和性质.
建议用时:15分钟
1 (2024南通通州月考)关于正比例函数y=-3x,下列结论中正确的是( )
A. 图象不经过原点 B. y随x的增大而增大
C. 图象经过第二、四象限 D. 当x=时,y=1
2 已知正比例函数y=(k+2)x(其中k为常数,且k≠-2),如果y的值随x的值增大而增大,那么下列k的值中,不可能的是( )
A. -3 B. -1 C. 0 D. 2
3 已知正比例函数y=-2x,则当x每增加1时,y的变化情况是( )
A. 增加1 B. 减少1 C. 增加2 D. 减少2
4 若正比例函数y=ax的图象经过第一、三象限,则直线y=(-a-1)x经过( )
A. 第一、三象限 B. 第二、三象限
C. 第二、四象限 D. 第三、四象限
5 (2025无锡一模)已知点P1(1,y1),P2(2,y2)在正比例函数y=-x的图象上,则y1 y2.(填“>”“<”或“=”)
6 若正比例函数y=(4-3m)x的值随x的值增大而减小,则m的取值范围为 .
7 (2024南通通州月考)已知正比例函数y=(m+1)xm2-3的图象经过第一、三象限,则m的值为 .
8 已知y=x,若y的取值范围是-1≤y≤1,则x的最小值为 .
9 已知y-2与3x-4成正比例函数关系,且当x=2时,y=3.
(1) 写出y与x之间的函数表达式;
(2) 若点P(a,-3)在这个函数的图象上,求a的值;
(3) 若y的取值范围为-1≤y≤1,求x的取值范围.
10 如图,在平面直角坐标系中,已知点A(1,3),B(n,3),若直线y=2x与线段AB有公共点,则n的值不可能是( )
A. B. 2 C. 3 D. 4
(第10题) (第11题) (第12题) (第13题)
11 如图是四个正比例函数的图象,则k1,k2,k3,k4的大小关系是( )
A. k1>k2>k3>k4 B. k3>k4>k1>k2
C. k3>k4>k2>k1 D. k4>k3>k2>k1
12 如图,已知直线l:y=x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点C,过点C作y轴的垂线交直线l于点D,则点D的坐标为 .
13 (2025南通如皋月考)如图,在平面直角坐标系xOy中,M是直线y=-2x上的动点,过点M作MN⊥x轴,交直线y=x于点N,当MN≤6时,设点M的横坐标为m,则m的取值范围为 .
14 如图,在平面直角坐标系中,点A(0,4),B(-2,0),点D在第一象限内,AD=6,AD∥x轴,DC∥AB交x轴于点C.
(1) 求四边形ABCD的面积;
(2) 已知直线y=x交AD于点E,点P在线段OE上.
①若S△PCD=S△BCD,求点P的坐标;
②设n=PC+PD,直接写出n的最小值.
第3课时 一次函数的图象
1. 会用描点法画一次函数图象,会判断点是否在一次函数图象上.
2. 通过平移,掌握正比例函数与一次函数图象的关系.
建议用时:15分钟
1 (2025南通月考)一次函数y=2x-4与x轴的交点坐标是( )
A. (0,-4) B. (0,4) C. (2,0) D. (-2,0)
2 (2024兰州)一次函数y=2x-3的图象不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3 (2024青海)如图,一次函数y=2x-3的图象与x轴相交于点A,则点A关于y轴的对称点的坐标是( )
A.(-,0) B.(,0)
C. (0,3) D. (0,-3)
4 (2025南通崇川月考)若直线y=kx+1经过点A(1,2),则k= .
5 (2024泰州姜堰期末)若点(m,n)在直线y=2x-1上,则代数式3n-6m+1的值是 .
6 (教材P155例3变式)已知一次函数y=-2x-2.
(1) 求图象与x轴,y轴的交点A,B的坐标;
(2) 画出函数的图象;
(3) 求A,B两点间的距离;
(4) 求△AOB的面积.
7 已知点(2,m),(1,2),(4,5)在同一条直线上,求m的值.
建议用时:20+5分钟
8 已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的是( )
A B C D
9 已知一次函数y=ax+b,若a-b=2,则它的图象必经过点( )
A. (1,-2) B. (-1,2) C. (-1,-2) D. (1,2)
10 当常数k,b满足kb>0时,一次函数y=kx+b的图象必经过的两个象限是 .
11 已知一次函数y=kx+4的图象经过点A(-3,-2).
(1) 求这个函数的表达式,并判断点B(-5,-3)是否在此函数的图象上;
(2) 求此函数与x轴,y轴围成的三角形的面积;
(3) 把该函数图象向下平移6个单位长度所得图象对应的函数表达式是 .
12 如图,正方形ABCD的边长为3,边BC在x轴上,BC的中点与原点O重合,过定点M(-2,0)与动点P(0,t)的直线MP记作l.
(1) 点A的坐标为 ,点D的坐标为 ;
(2) 若直线l的表达式为y=2x+4,判断此时点A是否在直线l上,并说明理由;
(3) 当直线l与边AD有公共点时,求t的取值范围.
第4课时 一次函数的性质
1. 掌握一次函数的图象特征和性质.
2. 会根据k和b的值,判断一次函数的图象经过哪几个象限.
建议用时:15分钟
1 (2024长沙)对于一次函数y=2x-1,下列结论中正确的是( )
A. 它的图象与y轴交于点(0,-1) B. y随x的增大而减小
C. 当x>时,y<0 D. 它的图象经过第一、二、三象限
2 (2024临夏州)若一次函数y=kx-1(k≠0)的函数值y随x的增大而减小,则它的图象不经过的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3 (2025扬州邗江期末)在同一平面直角坐标系中,函数y=-kx(k≠0)与y=-3x+k的图象大致是( )
A B C D
4 (2024镇江)若点A(1,y1),B(2,y2)在一次函数y=3x+1的图象上,则y1 y2.(填“>”“<”或“=”)
5 (2024南通海安期末)已知将直线y=-2x向下平移后得到直线l,若直线l经过点(a,b),且2a+b=-9,则直线l的表达式为 .
6 (2025常州模拟)已知A(3,y1),B(4,y2)是直线y=(k-2)x+b上的两点,若y1<y2,则k的取值范围是 .
7 (2025扬州邗江期末)已知一次函数y=x-m+6(m为常数)的图象与y轴的交点在x轴的下方,则m的取值范围为 .
8 已知一次函数y=-x+4,当0≤x≤2时,y的最大值为 .
9 已知一次函数y=(2m+4)x+(3-n).
(1) 当m,n满足什么条件时,y随x的增大而增大?
(2) 当m,n满足什么条件时,函数图象经过原点?
(3) 若函数图象经过第一、二、三象限,求m,n的取值范围.
建议用时:20+5分钟
10 (2025盐城阜宁期末)若点P在一次函数y=kx+4(k>0)的图象上,则点P一定不在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
11 (2024南京玄武月考)对于一次函数y=kx+k-1(k≠0),有下列说法:①当k<0时,y随x的增大而减小;②当k>2时,函数图象一定交y轴于负半轴;③当k=1时,函数图象经过原点;④函数图象一定经过点(-1,-2).其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
12 (2024南京期末)已知一次函数y1=k1x+b,y2=k2x+b与y3=k3x+b的图象如图所示,则k1,k2,k3的大小关系是 .(用“<”连接)
13 (2025南通月考)已知一次函数y=mx-2m(m为常数),当-1≤x≤3时,y有最大值6,则m的值为 .
14 已知一次函数y=(1-m)x+3-m的图象不经过第三象限,则正整数m的值为 .
15 在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点A(1,0)和B(2,-2).
(1) 当-1<x≤3时,求y的取值范围;
(2) 若点P(m,n)在该函数的图象上,且m-n=3,求点P的坐标;
(3) 若点Q在y轴上,且S△AQB=3,求点Q的坐标.
16 (2025盐城东台月考)如图,直线y=-x+与y轴交于点A,与x轴交于点B,点C,D在直线x=2(直线上所有点的横坐标均为2)上,且CD=.
(1) 求A,B两点的坐标;
(2) 四边形OACD的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
5.3 一次函数的图象与性质
第1课时 正比例函数的图象
1. A 2. B 3. B 4. A 5. A 6. (1,2) 原点 7. 2
8. 二、四
9. 解:(1) 将点(3,-6)代入y=kx,得-6=3k,解得k=-2,
所以这个函数的表达式为y=-2x.
(2) 如图,函数图象过点(0,0),(1,-2).
(3) 将点A(4,-2),B(-1.5,3)的坐标分别代入函数表达式,得-2≠-2×4,3=-2×(-1.5),
所以点A不在函数图象上,点B在函数图象上.
10. C 11. 4 12. 4 13. (22 024,22 024)
14. 解:(1) 因为点A(1,4)在正比例函数y=mx的图象上,
所以4=1×m,所以m=4.
因为点B(3,n)在正比例函数y=x的图象上,
所以n=×3=2,
所以m的值为4,n的值为2.
(2) 如图,作点B关于x轴的对称点B′,连接AB′交x轴于点P,此时PA+PB的值最小,最小值为线段AB′的长.
因为点B的坐标为(3,2),所以点B′的坐标为(3,-2),
所以线段AB′的长为=2,
所以PA+PB的最小值为2.
15. 解:(1)
(2) k的值不会发生变化.理由如下:
因为正方形ABCD的边长为a,所以AB=a.
在y=2x中,当y=a时,x=,
所以OA=,OD=+a=a,
所以点C(a,a),
所以a=k×a,
解得k=.
第2课时 正比例函数的性质
1. C 2. A 3. D 4. C 5. > 6. m> 7. 2
8. -
9. 解:(1) 设y-2=k(3x-4),
将x=2,y=3代入,得2k=1,解得k=,
所以y-2=(3x-4),即函数表达式为y=x.
(2) 由题意,得a=-3,
解得a=-2.
(3) 当y=-1时,x=-1,解得x=-;
当y=1时,x=1,解得x=,
所以-≤x≤.
10. A 11. B 12. (10,5) 13. -2≤m≤2
14. 解:(1) 因为点A(0,4),B(-2,0),点D在第一象限内,AD=6,AD∥x轴,DC∥AB交x轴于点C,
所以D(6,4),C(4,0),
所以S四边形ABCD=AD·AO=6×4=24.
(2) ①因为S△BCD=S四边形ABCD=×24=12,
所以S△PCD=S△BCD=×12=6.
设点P(m,m).
因为S△PCD=S梯形OCDE-S△POC-S△PED=6,E(4,4),
所以×(4+2)×4-×4×m-×2×(4-m)=6,
解得m=2,所以点P的坐标为(2,2).
②易得点A,C关于直线y=x对称,
所以当点P在点E处时,PC+PD取最小值,
此时n=ED+EC=ED+EA=6,
所以n的最小值为6.
第3课时 一次函数的图象
1. C 2. B 3. A 4. 1 5. -2
6. 解:(1) 当y=0时,-2x-2=0,解得x=-1,即A(-1,0);
当x=0时,y=-2,即B(0,-2).
(2) 如图,即为所求图象.
(3) 由勾股定理,得AB==.
(4) 由题意可得S△AOB=×1×2=1.
7. 解:设直线的表达式为y=kx+b,过点(1,2),(4,5),
则 解得
所以y=x+1.
因为点(2,m),(1,2),(4,5)在同一条直线上,
所以m=2+1=3.
8. D 9. C 10. 第二、三象限
11. 解: (1) 将点A(-3,-2)的坐标代入y=kx+4,得-3k+4=-2,
解得k=2,
所以这个函数的表达式是y=2x+4.
当x=-5时,y=-5×2+4=-6≠-3,
所以点B(-5,-3)不在此函数的图象上.
(2) 在y=2x+4中,令x=0,得y=4;
令y=0,得x=-2,
所以此函数与x轴,y轴围成的三角形的面积为×4×2=4.
(3) y=2x-2
12. 解:(1) (-,3) (,3)
(2) 当x=-时,y=2x+4=2×(-)+4=1≠3,
故点A不在直线l上.
(3) 因为直线l过点P,则设直线l的表达式为y=kx+t,
将点M的坐标代入上式,得0=-2k+t,解得k=t,
则直线l的表达式为y=tx+t.
当直线l过点A时,3=-×t+t=t,解得t=12;
当直线l过点D时,3=×t+t=t,解得t=.
故t的取值范围为≤t≤12.
第4课时 一次函数的性质
1. A 2. A 3. D 4. < 5. y=-2x-9 6. k>2
7. m>6 8. 4
9. 解:(1) m>-2,n取任何实数.
(2) m≠-2,n=3.
(3) m>-2,n<3.
10. D 11. B 12. k2<k3<k1 13. 6或-2 14. 2或3
15. 解:(1) 将点A(1,0)和B(2,-2)的坐标代入y=kx+b,
得解得
所以这个一次函数的表达式为y=-2x+2.
将x=-1代入y=-2x+2,得y=4;
将x=3代入y=-2x+2,得y=-4,
所以y的取值范围是-4≤y<4.
(2) 因为点P(m,n)在该函数的图象上,
所以n=-2m+2.
因为m-n=3,所以m-(-2m+2)=3,
解得m=,n=-,
所以点P的坐标为(,-).
(3) 设点Q的坐标为(0,a).
因为直线y=-2x+2与y轴的交点坐标为(0,2),
所以S△AQB=|a-2|×(2-1)=3,
解得a=8或a=-4,
所以点Q的坐标为(0,8)或(0,-4).
16. 解:(1) 在一次函数中,令x=0,则y=,
所以点A(0,);
令y=0,即-x+=0,解得x=6,
所以点B(6,0).
(2) 如图,将线段AC向下平移个单位长度到A′D,作出点O关于直线x=2的对称点O′,连接DO′,当点A′,D,O′三点在同一直线上时,此时四边形OACD的周长最小.
由图象,得AA′=CD=,AC=A′D,
所以点A′(0,3).
由对称可知点O′(4,0),OD=O′D,
所以A′O′=5,
所以四边形OACD周长的最小值为++5=11.
第1课时 正比例函数的图象
会用描点法画正比例函数的图象,正比例函数的图象过原点.
建议用时:15分钟
1 (2025南通月考)若正比例函数的图象经过点(-5,6),则这个图象必经过( )
A. (5,-6) B. (-6,5) C. (5,6) D. (-5,-6)
2 正比例函数y=x的大致图象是( )
A B C D
3 已知A(-3,4),B(2,-3),C(3,-4),D(-5,)四个点,则与其他三个点不在同一正比例函数图象上的是( )
A. 点A B. 点B C. 点C D. 点D
4 (2024德阳)若正比例函数y=kx(k≠0)的图象如图所示,则k的值可能是( )
A. B. -
C. -1 D. -
5 若P(a,b)是正比例函数y=-x图象上任意一点,则下列等式中一定成立的是( )
A. 2a+3b=0 B. 2a-3b=0 C. 3a+2b=0 D. 3a-2b=0
6 画正比例函数y=2x的图象,比较简单的方法是过点 和 作一直线即可得到.
7 (2025无锡宜兴月考)如果点A(-3,-6),B(1,m)在同一正比例函数的图象上,那么m的值为 .
8 正比例函数y=-x的图象平分第 象限.
9 已知正比例函数y=kx的图象经过点(3,-6).
(1) 求这个函数的表达式;
(2) 画出这个函数的图象;
(3) 判断点A(4,-2),B(-1.5,3)是否在这个函数图象上.
建议用时:20+5分钟
10 函数y=|2x|的图象是( )
A B C D
11 (2025南通海门月考)如图,已知正比例函数y=x和y=3x,过点A(2,0)作x轴的垂线,与这两个正比例函数的图象分别交于B,C两点,则△OBC的面积为 .
(第11题) (第12题) (第13题)
12 如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点A′在直线y=x上,则点A与点A′之间的距离为 .
13 如图,在平面直角坐标系中,依次在x轴上排列的正方形都有一个顶点在直线y=x上,从左到右分别记作点P1,P2,P3,…,Pn,已知顶点P1的坐标是(1,1),则点P2 025的坐标为 .
14 如图,点A(1,4)在正比例函数y=mx的图象上,点B(3,n)在正比例函数y=x的图象上.
(1) 求m,n的值;
(2) 在x轴上找一点P,使得PA+PB的值最小,请求出PA+PB的最小值.
15 如图,已知四边形ABCD是正方形,点B,C分别在两条直线y=2x和y=kx上,A,D是x轴上的两点.
(1) 若此正方形的边长为2,则k= ;
(2) 若此正方形的边长为a,k的值是否会发生变化?若不会发生变化,请说明理由;若会发生变化,求出a的值.
第2课时 正比例函数的性质
掌握正比例函数的图象特征和性质.
建议用时:15分钟
1 (2024南通通州月考)关于正比例函数y=-3x,下列结论中正确的是( )
A. 图象不经过原点 B. y随x的增大而增大
C. 图象经过第二、四象限 D. 当x=时,y=1
2 已知正比例函数y=(k+2)x(其中k为常数,且k≠-2),如果y的值随x的值增大而增大,那么下列k的值中,不可能的是( )
A. -3 B. -1 C. 0 D. 2
3 已知正比例函数y=-2x,则当x每增加1时,y的变化情况是( )
A. 增加1 B. 减少1 C. 增加2 D. 减少2
4 若正比例函数y=ax的图象经过第一、三象限,则直线y=(-a-1)x经过( )
A. 第一、三象限 B. 第二、三象限
C. 第二、四象限 D. 第三、四象限
5 (2025无锡一模)已知点P1(1,y1),P2(2,y2)在正比例函数y=-x的图象上,则y1 y2.(填“>”“<”或“=”)
6 若正比例函数y=(4-3m)x的值随x的值增大而减小,则m的取值范围为 .
7 (2024南通通州月考)已知正比例函数y=(m+1)xm2-3的图象经过第一、三象限,则m的值为 .
8 已知y=x,若y的取值范围是-1≤y≤1,则x的最小值为 .
9 已知y-2与3x-4成正比例函数关系,且当x=2时,y=3.
(1) 写出y与x之间的函数表达式;
(2) 若点P(a,-3)在这个函数的图象上,求a的值;
(3) 若y的取值范围为-1≤y≤1,求x的取值范围.
10 如图,在平面直角坐标系中,已知点A(1,3),B(n,3),若直线y=2x与线段AB有公共点,则n的值不可能是( )
A. B. 2 C. 3 D. 4
(第10题) (第11题) (第12题) (第13题)
11 如图是四个正比例函数的图象,则k1,k2,k3,k4的大小关系是( )
A. k1>k2>k3>k4 B. k3>k4>k1>k2
C. k3>k4>k2>k1 D. k4>k3>k2>k1
12 如图,已知直线l:y=x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点C,过点C作y轴的垂线交直线l于点D,则点D的坐标为 .
13 (2025南通如皋月考)如图,在平面直角坐标系xOy中,M是直线y=-2x上的动点,过点M作MN⊥x轴,交直线y=x于点N,当MN≤6时,设点M的横坐标为m,则m的取值范围为 .
14 如图,在平面直角坐标系中,点A(0,4),B(-2,0),点D在第一象限内,AD=6,AD∥x轴,DC∥AB交x轴于点C.
(1) 求四边形ABCD的面积;
(2) 已知直线y=x交AD于点E,点P在线段OE上.
①若S△PCD=S△BCD,求点P的坐标;
②设n=PC+PD,直接写出n的最小值.
第3课时 一次函数的图象
1. 会用描点法画一次函数图象,会判断点是否在一次函数图象上.
2. 通过平移,掌握正比例函数与一次函数图象的关系.
建议用时:15分钟
1 (2025南通月考)一次函数y=2x-4与x轴的交点坐标是( )
A. (0,-4) B. (0,4) C. (2,0) D. (-2,0)
2 (2024兰州)一次函数y=2x-3的图象不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3 (2024青海)如图,一次函数y=2x-3的图象与x轴相交于点A,则点A关于y轴的对称点的坐标是( )
A.(-,0) B.(,0)
C. (0,3) D. (0,-3)
4 (2025南通崇川月考)若直线y=kx+1经过点A(1,2),则k= .
5 (2024泰州姜堰期末)若点(m,n)在直线y=2x-1上,则代数式3n-6m+1的值是 .
6 (教材P155例3变式)已知一次函数y=-2x-2.
(1) 求图象与x轴,y轴的交点A,B的坐标;
(2) 画出函数的图象;
(3) 求A,B两点间的距离;
(4) 求△AOB的面积.
7 已知点(2,m),(1,2),(4,5)在同一条直线上,求m的值.
建议用时:20+5分钟
8 已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的是( )
A B C D
9 已知一次函数y=ax+b,若a-b=2,则它的图象必经过点( )
A. (1,-2) B. (-1,2) C. (-1,-2) D. (1,2)
10 当常数k,b满足kb>0时,一次函数y=kx+b的图象必经过的两个象限是 .
11 已知一次函数y=kx+4的图象经过点A(-3,-2).
(1) 求这个函数的表达式,并判断点B(-5,-3)是否在此函数的图象上;
(2) 求此函数与x轴,y轴围成的三角形的面积;
(3) 把该函数图象向下平移6个单位长度所得图象对应的函数表达式是 .
12 如图,正方形ABCD的边长为3,边BC在x轴上,BC的中点与原点O重合,过定点M(-2,0)与动点P(0,t)的直线MP记作l.
(1) 点A的坐标为 ,点D的坐标为 ;
(2) 若直线l的表达式为y=2x+4,判断此时点A是否在直线l上,并说明理由;
(3) 当直线l与边AD有公共点时,求t的取值范围.
第4课时 一次函数的性质
1. 掌握一次函数的图象特征和性质.
2. 会根据k和b的值,判断一次函数的图象经过哪几个象限.
建议用时:15分钟
1 (2024长沙)对于一次函数y=2x-1,下列结论中正确的是( )
A. 它的图象与y轴交于点(0,-1) B. y随x的增大而减小
C. 当x>时,y<0 D. 它的图象经过第一、二、三象限
2 (2024临夏州)若一次函数y=kx-1(k≠0)的函数值y随x的增大而减小,则它的图象不经过的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3 (2025扬州邗江期末)在同一平面直角坐标系中,函数y=-kx(k≠0)与y=-3x+k的图象大致是( )
A B C D
4 (2024镇江)若点A(1,y1),B(2,y2)在一次函数y=3x+1的图象上,则y1 y2.(填“>”“<”或“=”)
5 (2024南通海安期末)已知将直线y=-2x向下平移后得到直线l,若直线l经过点(a,b),且2a+b=-9,则直线l的表达式为 .
6 (2025常州模拟)已知A(3,y1),B(4,y2)是直线y=(k-2)x+b上的两点,若y1<y2,则k的取值范围是 .
7 (2025扬州邗江期末)已知一次函数y=x-m+6(m为常数)的图象与y轴的交点在x轴的下方,则m的取值范围为 .
8 已知一次函数y=-x+4,当0≤x≤2时,y的最大值为 .
9 已知一次函数y=(2m+4)x+(3-n).
(1) 当m,n满足什么条件时,y随x的增大而增大?
(2) 当m,n满足什么条件时,函数图象经过原点?
(3) 若函数图象经过第一、二、三象限,求m,n的取值范围.
建议用时:20+5分钟
10 (2025盐城阜宁期末)若点P在一次函数y=kx+4(k>0)的图象上,则点P一定不在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
11 (2024南京玄武月考)对于一次函数y=kx+k-1(k≠0),有下列说法:①当k<0时,y随x的增大而减小;②当k>2时,函数图象一定交y轴于负半轴;③当k=1时,函数图象经过原点;④函数图象一定经过点(-1,-2).其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
12 (2024南京期末)已知一次函数y1=k1x+b,y2=k2x+b与y3=k3x+b的图象如图所示,则k1,k2,k3的大小关系是 .(用“<”连接)
13 (2025南通月考)已知一次函数y=mx-2m(m为常数),当-1≤x≤3时,y有最大值6,则m的值为 .
14 已知一次函数y=(1-m)x+3-m的图象不经过第三象限,则正整数m的值为 .
15 在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点A(1,0)和B(2,-2).
(1) 当-1<x≤3时,求y的取值范围;
(2) 若点P(m,n)在该函数的图象上,且m-n=3,求点P的坐标;
(3) 若点Q在y轴上,且S△AQB=3,求点Q的坐标.
16 (2025盐城东台月考)如图,直线y=-x+与y轴交于点A,与x轴交于点B,点C,D在直线x=2(直线上所有点的横坐标均为2)上,且CD=.
(1) 求A,B两点的坐标;
(2) 四边形OACD的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
5.3 一次函数的图象与性质
第1课时 正比例函数的图象
1. A 2. B 3. B 4. A 5. A 6. (1,2) 原点 7. 2
8. 二、四
9. 解:(1) 将点(3,-6)代入y=kx,得-6=3k,解得k=-2,
所以这个函数的表达式为y=-2x.
(2) 如图,函数图象过点(0,0),(1,-2).
(3) 将点A(4,-2),B(-1.5,3)的坐标分别代入函数表达式,得-2≠-2×4,3=-2×(-1.5),
所以点A不在函数图象上,点B在函数图象上.
10. C 11. 4 12. 4 13. (22 024,22 024)
14. 解:(1) 因为点A(1,4)在正比例函数y=mx的图象上,
所以4=1×m,所以m=4.
因为点B(3,n)在正比例函数y=x的图象上,
所以n=×3=2,
所以m的值为4,n的值为2.
(2) 如图,作点B关于x轴的对称点B′,连接AB′交x轴于点P,此时PA+PB的值最小,最小值为线段AB′的长.
因为点B的坐标为(3,2),所以点B′的坐标为(3,-2),
所以线段AB′的长为=2,
所以PA+PB的最小值为2.
15. 解:(1)
(2) k的值不会发生变化.理由如下:
因为正方形ABCD的边长为a,所以AB=a.
在y=2x中,当y=a时,x=,
所以OA=,OD=+a=a,
所以点C(a,a),
所以a=k×a,
解得k=.
第2课时 正比例函数的性质
1. C 2. A 3. D 4. C 5. > 6. m> 7. 2
8. -
9. 解:(1) 设y-2=k(3x-4),
将x=2,y=3代入,得2k=1,解得k=,
所以y-2=(3x-4),即函数表达式为y=x.
(2) 由题意,得a=-3,
解得a=-2.
(3) 当y=-1时,x=-1,解得x=-;
当y=1时,x=1,解得x=,
所以-≤x≤.
10. A 11. B 12. (10,5) 13. -2≤m≤2
14. 解:(1) 因为点A(0,4),B(-2,0),点D在第一象限内,AD=6,AD∥x轴,DC∥AB交x轴于点C,
所以D(6,4),C(4,0),
所以S四边形ABCD=AD·AO=6×4=24.
(2) ①因为S△BCD=S四边形ABCD=×24=12,
所以S△PCD=S△BCD=×12=6.
设点P(m,m).
因为S△PCD=S梯形OCDE-S△POC-S△PED=6,E(4,4),
所以×(4+2)×4-×4×m-×2×(4-m)=6,
解得m=2,所以点P的坐标为(2,2).
②易得点A,C关于直线y=x对称,
所以当点P在点E处时,PC+PD取最小值,
此时n=ED+EC=ED+EA=6,
所以n的最小值为6.
第3课时 一次函数的图象
1. C 2. B 3. A 4. 1 5. -2
6. 解:(1) 当y=0时,-2x-2=0,解得x=-1,即A(-1,0);
当x=0时,y=-2,即B(0,-2).
(2) 如图,即为所求图象.
(3) 由勾股定理,得AB==.
(4) 由题意可得S△AOB=×1×2=1.
7. 解:设直线的表达式为y=kx+b,过点(1,2),(4,5),
则 解得
所以y=x+1.
因为点(2,m),(1,2),(4,5)在同一条直线上,
所以m=2+1=3.
8. D 9. C 10. 第二、三象限
11. 解: (1) 将点A(-3,-2)的坐标代入y=kx+4,得-3k+4=-2,
解得k=2,
所以这个函数的表达式是y=2x+4.
当x=-5时,y=-5×2+4=-6≠-3,
所以点B(-5,-3)不在此函数的图象上.
(2) 在y=2x+4中,令x=0,得y=4;
令y=0,得x=-2,
所以此函数与x轴,y轴围成的三角形的面积为×4×2=4.
(3) y=2x-2
12. 解:(1) (-,3) (,3)
(2) 当x=-时,y=2x+4=2×(-)+4=1≠3,
故点A不在直线l上.
(3) 因为直线l过点P,则设直线l的表达式为y=kx+t,
将点M的坐标代入上式,得0=-2k+t,解得k=t,
则直线l的表达式为y=tx+t.
当直线l过点A时,3=-×t+t=t,解得t=12;
当直线l过点D时,3=×t+t=t,解得t=.
故t的取值范围为≤t≤12.
第4课时 一次函数的性质
1. A 2. A 3. D 4. < 5. y=-2x-9 6. k>2
7. m>6 8. 4
9. 解:(1) m>-2,n取任何实数.
(2) m≠-2,n=3.
(3) m>-2,n<3.
10. D 11. B 12. k2<k3<k1 13. 6或-2 14. 2或3
15. 解:(1) 将点A(1,0)和B(2,-2)的坐标代入y=kx+b,
得解得
所以这个一次函数的表达式为y=-2x+2.
将x=-1代入y=-2x+2,得y=4;
将x=3代入y=-2x+2,得y=-4,
所以y的取值范围是-4≤y<4.
(2) 因为点P(m,n)在该函数的图象上,
所以n=-2m+2.
因为m-n=3,所以m-(-2m+2)=3,
解得m=,n=-,
所以点P的坐标为(,-).
(3) 设点Q的坐标为(0,a).
因为直线y=-2x+2与y轴的交点坐标为(0,2),
所以S△AQB=|a-2|×(2-1)=3,
解得a=8或a=-4,
所以点Q的坐标为(0,8)或(0,-4).
16. 解:(1) 在一次函数中,令x=0,则y=,
所以点A(0,);
令y=0,即-x+=0,解得x=6,
所以点B(6,0).
(2) 如图,将线段AC向下平移个单位长度到A′D,作出点O关于直线x=2的对称点O′,连接DO′,当点A′,D,O′三点在同一直线上时,此时四边形OACD的周长最小.
由图象,得AA′=CD=,AC=A′D,
所以点A′(0,3).
由对称可知点O′(4,0),OD=O′D,
所以A′O′=5,
所以四边形OACD周长的最小值为++5=11.
同课章节目录
