5.5 一次函数与二元一次方程 同步练(含答案)2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 5.5 一次函数与二元一次方程 同步练(含答案)2025-2026学年数学苏科版(2024)八年级上册 | 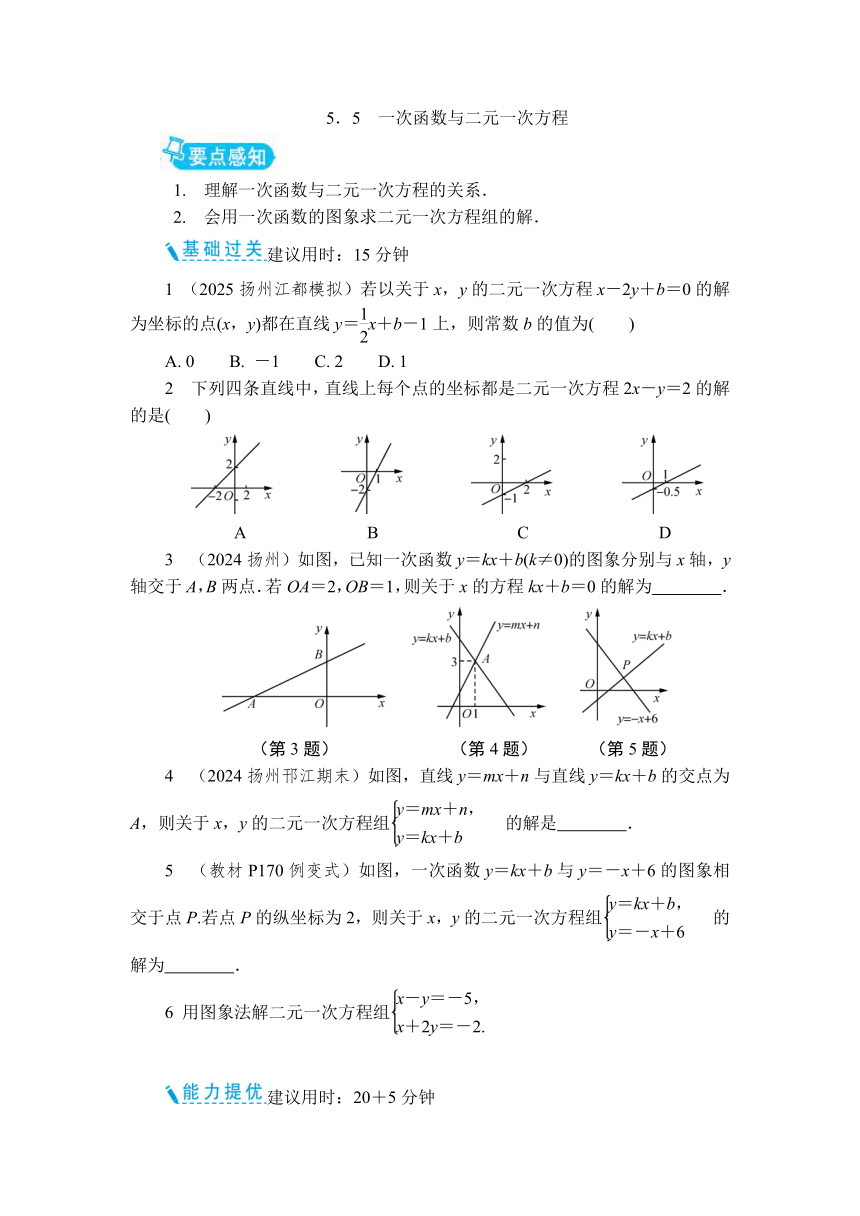 | |
| 格式 | docx | ||
| 文件大小 | 143.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 15:34:55 | ||
图片预览


文档简介
5.5 一次函数与二元一次方程
1. 理解一次函数与二元一次方程的关系.
2. 会用一次函数的图象求二元一次方程组的解.
建议用时:15分钟
1 (2025扬州江都模拟)若以关于x,y的二元一次方程x-2y+b=0的解为坐标的点(x,y)都在直线y=x+b-1上,则常数b的值为( )
A. 0 B. -1 C. 2 D. 1
2 下列四条直线中,直线上每个点的坐标都是二元一次方程2x-y=2的解的是( )
A B C D
3 (2024扬州)如图,已知一次函数y=kx+b(k≠0)的图象分别与x轴,y轴交于A,B两点.若OA=2,OB=1,则关于x的方程kx+b=0的解为 .
(第3题) (第4题) (第5题)
4 (2024扬州邗江期末)如图,直线y=mx+n与直线y=kx+b的交点为A,则关于x,y的二元一次方程组的解是 .
5 (教材P170例变式)如图,一次函数y=kx+b与y=-x+6的图象相交于点P.若点P的纵坐标为2,则关于x,y的二元一次方程组的解为 .
6 用图象法解二元一次方程组
建议用时:20+5分钟
7 (2024海州期末)如图,一次函数y=x+的图象与y=kx+b的图象相交于点P(-2,n),则关于x,y的方程组
的解是( )
A. B.
C. D.
8 在同一平面直角坐标系中,直线y=4x+1与直线y=-x+b的交点不可能在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
9 已知直线l1与l2相交于点P,点P的横坐标为-1,直线l2交x轴于点A(1,0),直线l1的表达式为y=2x+4,则直线l2的表达式为 .
10 (2024梁溪二模)已知函数y=
与关于x,y的二元一次方程ax-2a-y=0有两组解,则a的取值范围是 .
11 如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b).
(1) 求b,m的值;
(2) 若垂直于x轴的直线x=a与直线l1,l2分别相交于点C,D,且线段CD的长为2,求a的值.
12 定义:我们把一次函数y=kx+b(k≠0)的图象与正比例函数y=-x的图象的交点称为一次函数y=kx+b(k≠0)图象的“亮点”,例如,求一次函数y=-2x-1图象的“亮点”时,联立方程
解得
则一次函数y=-2x-1图象的“亮点”为(-1,1).
(1) 一次函数y=2x-3图象的“亮点”为 ;
(2) 一次函数y=mx+n图象的“亮点”为(2,n+1),求m,n的值;
(3) 若一次函数y=kx+4(k≠0)的图象分别与x轴,y轴交于A,B两点,且一次函数y=kx+4的图象上没有“亮点”,点P在y轴上,S△ABP=S△AOB,请直接写出满足条件的点P的坐标.
5.5 一次函数与二元一次方程
1. C 2. B 3. x=-2 4. 5.
6. 解:由x-y=-5,得y=x+5.
由x+2y=-2,得y=-x-1.
如图,在同一平面直角坐标系中,画出一次函数y=x+5,y=-x-1的图象,它们的交点坐标是(-4,1).
故二元一次方程组的解为
7. B 8. D 9. y=-x+1 10. -1<a≤-
11. 解:(1) 因为点P(1,b)在直线l1:y=2x+1上,
所以b=2×1+1=3.
因为点P(1,3)在直线l2:y=mx+4上,
所以3=m+4,所以m=-1.
(2) 当x=a时,yC=2a+1,yD=4-a.
因为CD=2,所以|2a+1-(4-a)|=2,
解得a=或a=.
12. 解:(1) (1,-1)
(2) 由题意可得点(2,n+1)在直线y=-x上,
所以n+1=-2,
解得n=-3.
因为点(2,n+1),即(2,-2)在直线y=mx+n上,
所以-2=2m-3,
解得m=.
(3) 因为直线y=kx+4上没有“亮点”,
所以直线y=kx+4与y=-x平行,
所以k=-1,
所以y=-x+4,
令x=0,则y=4,
令y=0,则x=4,
所以点A的坐标为(4,0),点B的坐标为(0,4),
所以OA=4,OB=4.
因为S△ABP=S△AOB,
即×BP×OA=××OA×OB,
所以BP=OB=3.
因为4+3=7,4-3=1,
所以点P的坐标为(0,7)或(0,1).
1. 理解一次函数与二元一次方程的关系.
2. 会用一次函数的图象求二元一次方程组的解.
建议用时:15分钟
1 (2025扬州江都模拟)若以关于x,y的二元一次方程x-2y+b=0的解为坐标的点(x,y)都在直线y=x+b-1上,则常数b的值为( )
A. 0 B. -1 C. 2 D. 1
2 下列四条直线中,直线上每个点的坐标都是二元一次方程2x-y=2的解的是( )
A B C D
3 (2024扬州)如图,已知一次函数y=kx+b(k≠0)的图象分别与x轴,y轴交于A,B两点.若OA=2,OB=1,则关于x的方程kx+b=0的解为 .
(第3题) (第4题) (第5题)
4 (2024扬州邗江期末)如图,直线y=mx+n与直线y=kx+b的交点为A,则关于x,y的二元一次方程组的解是 .
5 (教材P170例变式)如图,一次函数y=kx+b与y=-x+6的图象相交于点P.若点P的纵坐标为2,则关于x,y的二元一次方程组的解为 .
6 用图象法解二元一次方程组
建议用时:20+5分钟
7 (2024海州期末)如图,一次函数y=x+的图象与y=kx+b的图象相交于点P(-2,n),则关于x,y的方程组
的解是( )
A. B.
C. D.
8 在同一平面直角坐标系中,直线y=4x+1与直线y=-x+b的交点不可能在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
9 已知直线l1与l2相交于点P,点P的横坐标为-1,直线l2交x轴于点A(1,0),直线l1的表达式为y=2x+4,则直线l2的表达式为 .
10 (2024梁溪二模)已知函数y=
与关于x,y的二元一次方程ax-2a-y=0有两组解,则a的取值范围是 .
11 如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b).
(1) 求b,m的值;
(2) 若垂直于x轴的直线x=a与直线l1,l2分别相交于点C,D,且线段CD的长为2,求a的值.
12 定义:我们把一次函数y=kx+b(k≠0)的图象与正比例函数y=-x的图象的交点称为一次函数y=kx+b(k≠0)图象的“亮点”,例如,求一次函数y=-2x-1图象的“亮点”时,联立方程
解得
则一次函数y=-2x-1图象的“亮点”为(-1,1).
(1) 一次函数y=2x-3图象的“亮点”为 ;
(2) 一次函数y=mx+n图象的“亮点”为(2,n+1),求m,n的值;
(3) 若一次函数y=kx+4(k≠0)的图象分别与x轴,y轴交于A,B两点,且一次函数y=kx+4的图象上没有“亮点”,点P在y轴上,S△ABP=S△AOB,请直接写出满足条件的点P的坐标.
5.5 一次函数与二元一次方程
1. C 2. B 3. x=-2 4. 5.
6. 解:由x-y=-5,得y=x+5.
由x+2y=-2,得y=-x-1.
如图,在同一平面直角坐标系中,画出一次函数y=x+5,y=-x-1的图象,它们的交点坐标是(-4,1).
故二元一次方程组的解为
7. B 8. D 9. y=-x+1 10. -1<a≤-
11. 解:(1) 因为点P(1,b)在直线l1:y=2x+1上,
所以b=2×1+1=3.
因为点P(1,3)在直线l2:y=mx+4上,
所以3=m+4,所以m=-1.
(2) 当x=a时,yC=2a+1,yD=4-a.
因为CD=2,所以|2a+1-(4-a)|=2,
解得a=或a=.
12. 解:(1) (1,-1)
(2) 由题意可得点(2,n+1)在直线y=-x上,
所以n+1=-2,
解得n=-3.
因为点(2,n+1),即(2,-2)在直线y=mx+n上,
所以-2=2m-3,
解得m=.
(3) 因为直线y=kx+4上没有“亮点”,
所以直线y=kx+4与y=-x平行,
所以k=-1,
所以y=-x+4,
令x=0,则y=4,
令y=0,则x=4,
所以点A的坐标为(4,0),点B的坐标为(0,4),
所以OA=4,OB=4.
因为S△ABP=S△AOB,
即×BP×OA=××OA×OB,
所以BP=OB=3.
因为4+3=7,4-3=1,
所以点P的坐标为(0,7)或(0,1).
同课章节目录
