第3章勾股定理达标检测卷 同步练(含答案) 2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 第3章勾股定理达标检测卷 同步练(含答案) 2025-2026学年数学苏科版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 369.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 15:19:13 | ||
图片预览




文档简介
第3章勾股定理达标检测卷
(时间:100分钟 满分:120分)
一、 选择题(每小题3分,共24分)
1. 在△ABC中,∠BAC=90°,则下列结论中正确的是( )
A. BC=AC+BA B. AC2=AB2+BC2
C. AB2=AC2+BC2 D. BC2=AB2+AC2
2. (2024连云港海州月考)下列条件中,不能判断△ABC是直角三角形的是( )
A. AB∶BC∶AC=3∶4∶5 B. AB∶BC∶AC=1∶2∶
C. ∠A-∠B=∠C D. ∠A∶∠B∶∠C=3∶4∶5
3. (2025常州期末)如图,根据尺规作图痕迹,点M在数轴上表示的数是( )
A. -1 B. C. +1 D. 5
(第3题) (第4题) (第5题)
4. 如图,正方形小方格的边长为1,则网格中的线段长为无理数的个数为( )
A. 4 B. 3 C. 2 D. 1
5. 如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于点M.若CM=3,则CE2+CF2的值为( )
A. 6 B. 9 C. 18 D. 36
6. 如图,在△ABC中,∠C=90°,AB的中垂线DE交AB于点E,交AC于点D.若AB=15,BC=9,则△BCD的周长为( )
A. 16 B. 20 C. 21 D. 24
(第6题) (第7题) (第8题)
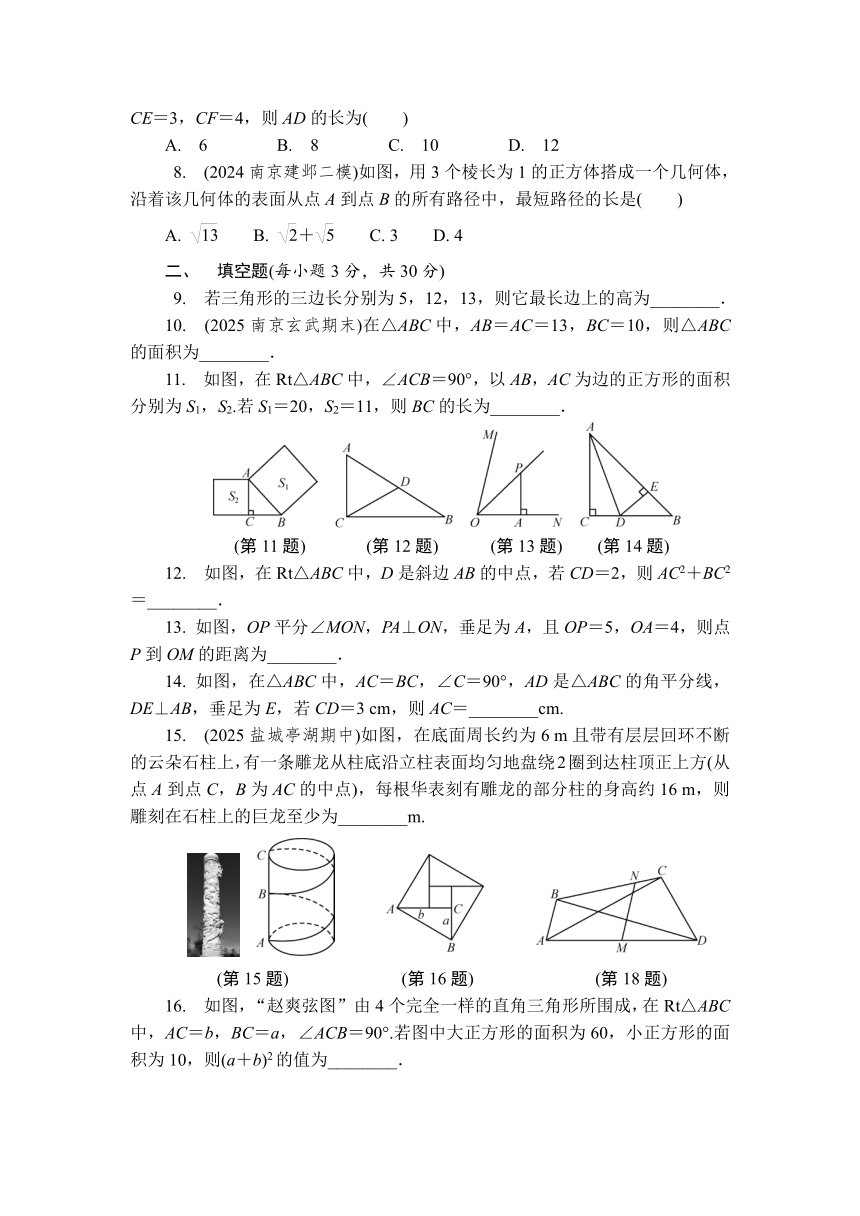
7. 如图,将长方形ABCD沿着AE折叠,点D落在边BC上的点F处.若CE=3,CF=4,则AD的长为( )
A. 6 B. 8 C. 10 D. 12
8. (2024南京建邺二模)如图,用3个棱长为1的正方体搭成一个几何体,沿着该几何体的表面从点A到点B的所有路径中,最短路径的长是( )
A. B. + C. 3 D. 4
二、 填空题(每小题3分,共30分)
9. 若三角形的三边长分别为5,12,13,则它最长边上的高为________.
10. (2025南京玄武期末)在△ABC中,AB=AC=13,BC=10,则△ABC的面积为________.
11. 如图,在Rt△ABC中,∠ACB=90°,以AB,AC为边的正方形的面积分别为S1,S2.若S1=20,S2=11,则BC的长为________.
(第11题) (第12题) (第13题) (第14题)
12. 如图,在Rt△ABC中,D是斜边AB的中点,若CD=2,则AC2+BC2=________.
13. 如图,OP平分∠MON,PA⊥ON,垂足为A,且OP=5,OA=4,则点P到OM的距离为________.
14. 如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,若CD=3 cm,则AC=________cm.
15. (2025盐城亭湖期中)如图,在底面周长约为6 m且带有层层回环不断的云朵石柱上,有一条雕龙从柱底沿立柱表面均匀地盘绕2圈到达柱顶正上方(从点A到点C,B为AC的中点),每根华表刻有雕龙的部分柱的身高约16 m,则雕刻在石柱上的巨龙至少为________m.
(第15题) (第16题) (第18题)
16. 如图,“赵爽弦图”由4个完全一样的直角三角形所围成,在Rt△ABC中,AC=b,BC=a,∠ACB=90°.若图中大正方形的面积为60,小正方形的面积为10,则(a+b)2的值为________.
17. (2025扬州广陵期中)观察下列勾股数组:①3,4,5;②5,12,13;③7,24,25;④9,40,41….若a,144,145是其中的一组勾股数,则a=________.(提示:5=,13=,…)
18. (2025泰州海陵期末)如图,在四边形ABCD中,∠ABD=∠ACD=90°,M是AD的中点,N是BC上的动点,连接MN.若AD=8,BC=6,则MN的最小值为________.
三、 解答题(共66分)
19. (6分)如图,在△ABC中,已知AB=AC=13 cm,BC=10 cm,AD⊥BC于点D,求AD的长.
20. (8分)如图,在△ABC中,AB的垂直平分线分别交AB,AC及BC的延长线于点D,E,F,且CB2=AE2-CE2.
(1) 求证:∠ACB=90°;
(2) 若AC=12,BC=9,求CE的长.
21. (8分)如图,在Rt△ABC中,∠C=90°.
(1) 在线段AC上找一点D,使得点D到AB,BC的距离相等(要求:尺规作图,保留作图痕迹,不写作法);
(2) 连接BD,若BC=6,AB=10,求AD的长.
22. (8分)(2025镇江丹徒期中)勾股定理体现了数与形的完美结合,小明在学习了教材中介绍的拼图证法以后突发灵感,发现新的拼图方法:如图,两个全等的直角三角板ABC和直角三角板DEF,顶点D在边BC上,顶点F,B重合,连接AE,AD.设AB,DE交于点G.已知∠ACB=∠DFE=90°,BC=EF=a,AC=DF=b(a>b),AB=DE=c.请你回答下列问题:
(1) ∠AGE=________,S四边形ADBE=________(用含字母c的代数式表示);
(2) 请用两种方法计算四边形ACBE的面积,并以此为基础证明勾股定理.
23. (8分)(2025连云港赣榆期中)2024年某文化旅游品牌活动在青秀山风景区拉开帷幕,大家身着民族服饰共赴一场民俗文化盛宴.如图,在地图上A,B两站的直线距离为25 km,C,D为青秀山和园博园民俗文化活动场地,且DA⊥AB于点A,CB⊥AB于点B.已知DA=15 km,CB=10 km,现在小明要在直线AB上找到地点E.
(1) 若要使得C,D两活动点到地点E的距离相等,则小明所在的E站应在距离A站多少 千米处?
(2) 若要使得地点E到C,D两地的距离之和最短,则小明所在的E站应在距离A站多少 千米处?
24. (8分)如图,在△ABC中,∠C=90°,AB=5 cm,BC=3 cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为1 cm/s,设出发的时间为t s.
(1) 若AP恰好是∠BAC的平分线,求t的值;
(2) 问当t为何值时,△BCP为等腰三角形?
25. (10分)在△ABC中,BC=a,CA=b,AB=c.若∠C为直角,则a2+b2=c2;若∠C为锐角或钝角,则a2+b2与c2之间有怎样的大小关系呢?我们一起进行探究吧.
(1) 阅读并填空:如图1,若∠C为锐角,则a2+b2>c2.
证明:如图2,过点A作AD⊥BC于点D,则BD=BC-CD=a-CD.
在Rt△ABD中,AD2=AB2-BD2,
在Rt△ACD中,AD2=________,
所以________,
即c2-(a-CD)2=b2-CD2,
所以a2+b2-c2=2a·CD.
因为a>0,CD>0,所以a2+b2-c2>0,即a2+b2>c2.
(2) 解答问题:如图3,若∠C为钝角,试推导a2+b2与c2的大小关系.
图1 图2 图3
26. (10分)(2025南京鼓楼期中)与直角三角形三条边长对应的3个正整数(a,b,c)称为勾股数,《周髀算经》中记载的“勾三股四弦五”中的“3,4,5”就是一组最简单的勾股数,显然,这组数的整数倍,如(6,8,10),(9,12,15),(12,16,20)等都是勾股数.当然,勾股数远远不止这些,如(5,12,13),(8,15,17)等也都是勾股数.怎样探索勾股数呢?即怎样一组正整数(a,b,c)才能满足关系式a2+b2=c2.设(a,b,c)为一组勾股数,观察下表回答问题:
表1 表2
a b c
3 4 5
5 12 13
7 24 25
9 40 41
a b c
6 8 10
8 15 17
10 24 26
12 35 37
(1) 根据表1的规律写出勾股数(11,________,________);
观察可得:表1中b,c与a2之间的关系是________(填勾股定理不得分);
(2) 根据表2的规律写出勾股数(16,________,________);
观察可得:表2中b,c与a2之间的关系是________(填勾股定理不得分);
(3) 老师告诉小明一组符合表1或表2的勾股数,但他回家后只记得其中最大的数是145,你知道这组勾股数可能是多少吗?(请用勾股定理的形式直接写出结果,例如32+42=52)
第3章勾股定理 达标检测卷
1. D 2. D 3. B 4. B 5. D 6. C 7. C 8. A
9. 10. 60 11. 3 12. 16 13. 3 14. 3+
15. 20 16. 110 17. 17 18.
19. 解:因为AB=AC,AD⊥BC,所以BD=BC=5 cm.
在Rt△ABD中,由勾股定理,得AD===12(cm),
所以AD的长为12 cm.
20. 解:(1) 连接BE.
因为ED垂直平分AB,所以AE=BE.
因为CB2=AE2-CE2,所以CB2=BE2-CE2,
所以CB2+CE2=BE2,
所以△BCE是直角三角形,
所以∠ACB=90°.
(2) 设CE=x,则AE=12-x.
因为BE=AE,所以BE=12-x.
在△BEC中,∠ECB=90°,BC=9,
所以CB2+CE2=BE2,
即92+x2=(12-x)2,解得x=,
所以CE的长为.
21. 解:(1) 如图,点D即为所求.
(2) 过点D作DT⊥AB于点T.
因为BD平分∠ABC,DC⊥BC,DT⊥BA,
所以DC=DT.
设DC=DT=x.
在△ABC中,∠C=90°,BC=6,AB=10,
所以AC===8.
因为S△ABC=AC·BC=BC·DC+·AB·DT,
所以6×8=6x+10x,解得x=3,
所以AD=AC-CD=8-3=5.
22. 解:(1) 90° c2
(2) 方法一:S四边形ACBE=(AC+EF)BC=(b+a)a=ab+a2;
方法二:S四边形ACBE=S△ACD+S四边形ADBE=b(a-b)+c2=ab-b2+c2.
根据上面的两种方法可得出 ab+a2=ab-b2+c2,
所以a2+b2=c2.
23. 解:(1) 因为C,D两活动点到地点E站的距离相等,
所以DE=CE.
因为DA⊥AB,CB⊥AB,
所以∠A=∠B=90°,
所以AE2+AD2=DE2,BE2+BC2=CE2,
所以AE2+AD2=BE2+BC2.
设AE=x km,则BE=AB-AE=(25-x)km.
因为DA=15 km,CB=10 km,
所以x2+152=(25-x)2+102,
解得x=10,即AE=10 km,
所以小明所在的E站应在距离A站10 km处.
(2) 作点D关于AB的对称点D′,连接CD′交AB于点E′,
则点E′到C,D两地的距离之和最短,过点D′作D′F⊥CB的延长线于点F,
则∠F=90°,D′F=AB=25,CF=CB+BF=CB+AD′=CB+AD=25,
所以D′F=CF.
易得E′C+E′D的最小值即为CD′,此时∠BCE′=45°,
则∠AE′D′=∠CE′B=45°,
所以∠AD′E′=∠AE′D=45°,
所以AE′=AD=15 km,
所以要使得地点E到C,D两地的距离之和最短,小明所在的E站应在距离A站15 km处.
24. 解:(1) 如图1,过点P作PE⊥AB,垂足为E.
因为AP恰好是∠BAC的平分线,且∠C=90°,AB=5 cm,BC=3 cm,
所以CP=EP,AC=4 cm.
又AP=AP,所以△ACP≌△AEP(HL),
所以AE=AC=4 cm,BE=5-4=1(cm).
设CP=x,则BP=3-x,PE=x,
所以在Rt△BEP中,BE2+PE2=BP2,
即12+x2=(3-x)2,解得x=,
所以BP=3-=(cm),
所以CA+AB+BP=4+5+=(cm),
此时t=÷1=.
故t的值为.
(2) 如图2,当CP=CB时,△BCP为等腰三角形,
若点P在CA上,则t==3;
如图3,当BP=BC=3 cm时,△BCP为等腰三角形,
则AP=AB-BP=2 cm,
所以t=(4+2)÷1=6;
如图4,若点P在AB上,CP=CB=3 cm,过点C作CD⊥AB于点D,则根据直角三角形的面积法,得CD=.
在Rt△BCD中,由勾股定理,得BD=,
所以PB=2BD=,
所以CA+AP=4+5-=5.4,
此时t=5.4÷1=5.4;
如图5,当PC=PB时,△BCP为等腰三角形,过点P作PD⊥BC于点D,则BD=CD,
所以AP=BP=AB=,
所以t=(4+)÷1=6.5.
综上所述,当t的值为3或5.4或6或6.5时,△BCP为等腰三角形.
图1 图2 图3 图4 图5
25. 解:(1) AC2-CD2 AB2-BD2=AC2-CD2
(2) a2+b2<c2.理由如下:
如图,过点A作AD⊥BC交BC的延长线于点D,
则BD=BC+CD=a+CD.
在Rt△ABD中,AD2=AB2-BD2,
在Rt△ACD中,AD2=AC2-CD2,
所以AB2-BD2=AC2-CD2,
即c2-(a+CD)2=b2-CD2,
所以a2+b2-c2=-2a·CD.
因为a>0,CD>0,所以a2+b2-c2<0,
即a2+b2<c2.
26. 解:(1) 60 61 a2=b+c
(2) 63 65 a2=b+c
(3) 当145符合表1时,中间的数为144,
因为145+144=289,且172=289,
所以这组勾股数为17,144,145;
当145符合表2时,中间的数为143,
因为145+143=288,且288×2=576,242=576,
所以这组勾股数是24,143,145.
综上,这组勾股数为17,144,145,即172+1442=1452或24,143,145,即242+1432=1452.
(时间:100分钟 满分:120分)
一、 选择题(每小题3分,共24分)
1. 在△ABC中,∠BAC=90°,则下列结论中正确的是( )
A. BC=AC+BA B. AC2=AB2+BC2
C. AB2=AC2+BC2 D. BC2=AB2+AC2
2. (2024连云港海州月考)下列条件中,不能判断△ABC是直角三角形的是( )
A. AB∶BC∶AC=3∶4∶5 B. AB∶BC∶AC=1∶2∶
C. ∠A-∠B=∠C D. ∠A∶∠B∶∠C=3∶4∶5
3. (2025常州期末)如图,根据尺规作图痕迹,点M在数轴上表示的数是( )
A. -1 B. C. +1 D. 5
(第3题) (第4题) (第5题)
4. 如图,正方形小方格的边长为1,则网格中的线段长为无理数的个数为( )
A. 4 B. 3 C. 2 D. 1
5. 如图,在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于点M.若CM=3,则CE2+CF2的值为( )
A. 6 B. 9 C. 18 D. 36
6. 如图,在△ABC中,∠C=90°,AB的中垂线DE交AB于点E,交AC于点D.若AB=15,BC=9,则△BCD的周长为( )
A. 16 B. 20 C. 21 D. 24
(第6题) (第7题) (第8题)
7. 如图,将长方形ABCD沿着AE折叠,点D落在边BC上的点F处.若CE=3,CF=4,则AD的长为( )
A. 6 B. 8 C. 10 D. 12
8. (2024南京建邺二模)如图,用3个棱长为1的正方体搭成一个几何体,沿着该几何体的表面从点A到点B的所有路径中,最短路径的长是( )
A. B. + C. 3 D. 4
二、 填空题(每小题3分,共30分)
9. 若三角形的三边长分别为5,12,13,则它最长边上的高为________.
10. (2025南京玄武期末)在△ABC中,AB=AC=13,BC=10,则△ABC的面积为________.
11. 如图,在Rt△ABC中,∠ACB=90°,以AB,AC为边的正方形的面积分别为S1,S2.若S1=20,S2=11,则BC的长为________.
(第11题) (第12题) (第13题) (第14题)
12. 如图,在Rt△ABC中,D是斜边AB的中点,若CD=2,则AC2+BC2=________.
13. 如图,OP平分∠MON,PA⊥ON,垂足为A,且OP=5,OA=4,则点P到OM的距离为________.
14. 如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,若CD=3 cm,则AC=________cm.
15. (2025盐城亭湖期中)如图,在底面周长约为6 m且带有层层回环不断的云朵石柱上,有一条雕龙从柱底沿立柱表面均匀地盘绕2圈到达柱顶正上方(从点A到点C,B为AC的中点),每根华表刻有雕龙的部分柱的身高约16 m,则雕刻在石柱上的巨龙至少为________m.
(第15题) (第16题) (第18题)
16. 如图,“赵爽弦图”由4个完全一样的直角三角形所围成,在Rt△ABC中,AC=b,BC=a,∠ACB=90°.若图中大正方形的面积为60,小正方形的面积为10,则(a+b)2的值为________.
17. (2025扬州广陵期中)观察下列勾股数组:①3,4,5;②5,12,13;③7,24,25;④9,40,41….若a,144,145是其中的一组勾股数,则a=________.(提示:5=,13=,…)
18. (2025泰州海陵期末)如图,在四边形ABCD中,∠ABD=∠ACD=90°,M是AD的中点,N是BC上的动点,连接MN.若AD=8,BC=6,则MN的最小值为________.
三、 解答题(共66分)
19. (6分)如图,在△ABC中,已知AB=AC=13 cm,BC=10 cm,AD⊥BC于点D,求AD的长.
20. (8分)如图,在△ABC中,AB的垂直平分线分别交AB,AC及BC的延长线于点D,E,F,且CB2=AE2-CE2.
(1) 求证:∠ACB=90°;
(2) 若AC=12,BC=9,求CE的长.
21. (8分)如图,在Rt△ABC中,∠C=90°.
(1) 在线段AC上找一点D,使得点D到AB,BC的距离相等(要求:尺规作图,保留作图痕迹,不写作法);
(2) 连接BD,若BC=6,AB=10,求AD的长.
22. (8分)(2025镇江丹徒期中)勾股定理体现了数与形的完美结合,小明在学习了教材中介绍的拼图证法以后突发灵感,发现新的拼图方法:如图,两个全等的直角三角板ABC和直角三角板DEF,顶点D在边BC上,顶点F,B重合,连接AE,AD.设AB,DE交于点G.已知∠ACB=∠DFE=90°,BC=EF=a,AC=DF=b(a>b),AB=DE=c.请你回答下列问题:
(1) ∠AGE=________,S四边形ADBE=________(用含字母c的代数式表示);
(2) 请用两种方法计算四边形ACBE的面积,并以此为基础证明勾股定理.
23. (8分)(2025连云港赣榆期中)2024年某文化旅游品牌活动在青秀山风景区拉开帷幕,大家身着民族服饰共赴一场民俗文化盛宴.如图,在地图上A,B两站的直线距离为25 km,C,D为青秀山和园博园民俗文化活动场地,且DA⊥AB于点A,CB⊥AB于点B.已知DA=15 km,CB=10 km,现在小明要在直线AB上找到地点E.
(1) 若要使得C,D两活动点到地点E的距离相等,则小明所在的E站应在距离A站多少 千米处?
(2) 若要使得地点E到C,D两地的距离之和最短,则小明所在的E站应在距离A站多少 千米处?
24. (8分)如图,在△ABC中,∠C=90°,AB=5 cm,BC=3 cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为1 cm/s,设出发的时间为t s.
(1) 若AP恰好是∠BAC的平分线,求t的值;
(2) 问当t为何值时,△BCP为等腰三角形?
25. (10分)在△ABC中,BC=a,CA=b,AB=c.若∠C为直角,则a2+b2=c2;若∠C为锐角或钝角,则a2+b2与c2之间有怎样的大小关系呢?我们一起进行探究吧.
(1) 阅读并填空:如图1,若∠C为锐角,则a2+b2>c2.
证明:如图2,过点A作AD⊥BC于点D,则BD=BC-CD=a-CD.
在Rt△ABD中,AD2=AB2-BD2,
在Rt△ACD中,AD2=________,
所以________,
即c2-(a-CD)2=b2-CD2,
所以a2+b2-c2=2a·CD.
因为a>0,CD>0,所以a2+b2-c2>0,即a2+b2>c2.
(2) 解答问题:如图3,若∠C为钝角,试推导a2+b2与c2的大小关系.
图1 图2 图3
26. (10分)(2025南京鼓楼期中)与直角三角形三条边长对应的3个正整数(a,b,c)称为勾股数,《周髀算经》中记载的“勾三股四弦五”中的“3,4,5”就是一组最简单的勾股数,显然,这组数的整数倍,如(6,8,10),(9,12,15),(12,16,20)等都是勾股数.当然,勾股数远远不止这些,如(5,12,13),(8,15,17)等也都是勾股数.怎样探索勾股数呢?即怎样一组正整数(a,b,c)才能满足关系式a2+b2=c2.设(a,b,c)为一组勾股数,观察下表回答问题:
表1 表2
a b c
3 4 5
5 12 13
7 24 25
9 40 41
a b c
6 8 10
8 15 17
10 24 26
12 35 37
(1) 根据表1的规律写出勾股数(11,________,________);
观察可得:表1中b,c与a2之间的关系是________(填勾股定理不得分);
(2) 根据表2的规律写出勾股数(16,________,________);
观察可得:表2中b,c与a2之间的关系是________(填勾股定理不得分);
(3) 老师告诉小明一组符合表1或表2的勾股数,但他回家后只记得其中最大的数是145,你知道这组勾股数可能是多少吗?(请用勾股定理的形式直接写出结果,例如32+42=52)
第3章勾股定理 达标检测卷
1. D 2. D 3. B 4. B 5. D 6. C 7. C 8. A
9. 10. 60 11. 3 12. 16 13. 3 14. 3+
15. 20 16. 110 17. 17 18.
19. 解:因为AB=AC,AD⊥BC,所以BD=BC=5 cm.
在Rt△ABD中,由勾股定理,得AD===12(cm),
所以AD的长为12 cm.
20. 解:(1) 连接BE.
因为ED垂直平分AB,所以AE=BE.
因为CB2=AE2-CE2,所以CB2=BE2-CE2,
所以CB2+CE2=BE2,
所以△BCE是直角三角形,
所以∠ACB=90°.
(2) 设CE=x,则AE=12-x.
因为BE=AE,所以BE=12-x.
在△BEC中,∠ECB=90°,BC=9,
所以CB2+CE2=BE2,
即92+x2=(12-x)2,解得x=,
所以CE的长为.
21. 解:(1) 如图,点D即为所求.
(2) 过点D作DT⊥AB于点T.
因为BD平分∠ABC,DC⊥BC,DT⊥BA,
所以DC=DT.
设DC=DT=x.
在△ABC中,∠C=90°,BC=6,AB=10,
所以AC===8.
因为S△ABC=AC·BC=BC·DC+·AB·DT,
所以6×8=6x+10x,解得x=3,
所以AD=AC-CD=8-3=5.
22. 解:(1) 90° c2
(2) 方法一:S四边形ACBE=(AC+EF)BC=(b+a)a=ab+a2;
方法二:S四边形ACBE=S△ACD+S四边形ADBE=b(a-b)+c2=ab-b2+c2.
根据上面的两种方法可得出 ab+a2=ab-b2+c2,
所以a2+b2=c2.
23. 解:(1) 因为C,D两活动点到地点E站的距离相等,
所以DE=CE.
因为DA⊥AB,CB⊥AB,
所以∠A=∠B=90°,
所以AE2+AD2=DE2,BE2+BC2=CE2,
所以AE2+AD2=BE2+BC2.
设AE=x km,则BE=AB-AE=(25-x)km.
因为DA=15 km,CB=10 km,
所以x2+152=(25-x)2+102,
解得x=10,即AE=10 km,
所以小明所在的E站应在距离A站10 km处.
(2) 作点D关于AB的对称点D′,连接CD′交AB于点E′,
则点E′到C,D两地的距离之和最短,过点D′作D′F⊥CB的延长线于点F,
则∠F=90°,D′F=AB=25,CF=CB+BF=CB+AD′=CB+AD=25,
所以D′F=CF.
易得E′C+E′D的最小值即为CD′,此时∠BCE′=45°,
则∠AE′D′=∠CE′B=45°,
所以∠AD′E′=∠AE′D=45°,
所以AE′=AD=15 km,
所以要使得地点E到C,D两地的距离之和最短,小明所在的E站应在距离A站15 km处.
24. 解:(1) 如图1,过点P作PE⊥AB,垂足为E.
因为AP恰好是∠BAC的平分线,且∠C=90°,AB=5 cm,BC=3 cm,
所以CP=EP,AC=4 cm.
又AP=AP,所以△ACP≌△AEP(HL),
所以AE=AC=4 cm,BE=5-4=1(cm).
设CP=x,则BP=3-x,PE=x,
所以在Rt△BEP中,BE2+PE2=BP2,
即12+x2=(3-x)2,解得x=,
所以BP=3-=(cm),
所以CA+AB+BP=4+5+=(cm),
此时t=÷1=.
故t的值为.
(2) 如图2,当CP=CB时,△BCP为等腰三角形,
若点P在CA上,则t==3;
如图3,当BP=BC=3 cm时,△BCP为等腰三角形,
则AP=AB-BP=2 cm,
所以t=(4+2)÷1=6;
如图4,若点P在AB上,CP=CB=3 cm,过点C作CD⊥AB于点D,则根据直角三角形的面积法,得CD=.
在Rt△BCD中,由勾股定理,得BD=,
所以PB=2BD=,
所以CA+AP=4+5-=5.4,
此时t=5.4÷1=5.4;
如图5,当PC=PB时,△BCP为等腰三角形,过点P作PD⊥BC于点D,则BD=CD,
所以AP=BP=AB=,
所以t=(4+)÷1=6.5.
综上所述,当t的值为3或5.4或6或6.5时,△BCP为等腰三角形.
图1 图2 图3 图4 图5
25. 解:(1) AC2-CD2 AB2-BD2=AC2-CD2
(2) a2+b2<c2.理由如下:
如图,过点A作AD⊥BC交BC的延长线于点D,
则BD=BC+CD=a+CD.
在Rt△ABD中,AD2=AB2-BD2,
在Rt△ACD中,AD2=AC2-CD2,
所以AB2-BD2=AC2-CD2,
即c2-(a+CD)2=b2-CD2,
所以a2+b2-c2=-2a·CD.
因为a>0,CD>0,所以a2+b2-c2<0,
即a2+b2<c2.
26. 解:(1) 60 61 a2=b+c
(2) 63 65 a2=b+c
(3) 当145符合表1时,中间的数为144,
因为145+144=289,且172=289,
所以这组勾股数为17,144,145;
当145符合表2时,中间的数为143,
因为145+143=288,且288×2=576,242=576,
所以这组勾股数是24,143,145.
综上,这组勾股数为17,144,145,即172+1442=1452或24,143,145,即242+1432=1452.
同课章节目录
