第4章 平面直角坐标系 达标检测卷 同步练 (含答案)2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 第4章 平面直角坐标系 达标检测卷 同步练 (含答案)2025-2026学年数学苏科版(2024)八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 200.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 15:16:04 | ||
图片预览



文档简介
第4章 平面直角坐标系 达标检测卷
(时间:100分钟 满分:120分)
一、 选择题(每小题3分,共24分)
1. (2025常州天宁月考)在平面直角坐标系中,点A(2,-4)到x轴的距离是( )
A. 4 B. 2 C. -4 D. -2
2. (2025南京期中)在平面直角坐标系中,点P(0,1)关于点A(1,0)对称的点的坐标为( )
A. (0,-1) B. (1,-1) C. (2,-1) D. (3,-1)
3. (2025南通海安月考)在平面直角坐标系中,将点A(m,2)先向右平移1个单位长度,再向上平移3个单位长度得到点B.若点B的横坐标和纵坐标相等,则m等于( )
A. 4 B. 5 C. 6 D. 7
4. (2024贵州)为培养青少年的科学态度和科学思维,某校创建了“科技创新”社团.小红将“科”“技”“创”“新”写在如图所示的方格纸中,若建立平面直角坐标系,使“创”“新”的坐标分别为(-2,0),(0,0),则“技”所在的象限为( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
(第4题) (第5题) (第6题) (第8题)
5. 如图,平面直角坐标系上有P,Q两点,其坐标分别为P(4,a),Q(b,6).根据图中P,Q两点的位置,判断点(-b,a-7)所在的象限为( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
6. (2025盐城射阳月考)如图,已知点A(1,3),B(4,1),将线段AB绕点M逆时针旋转到A′B′,点A与A′是对应点,点B与B′是对应点,则点M的坐标是( )
A. (-1,-2) B. (1,0) C. (-1,1) D. (1,-3)
7. 已知点P的坐标为(1-a,2a+4),且点P到两坐标轴的距离相等,则点P的坐标是( )
A. (2,2) B. (2,-2)
C. (6,-6) D. (2,2)或(6,-6)
8. 如图,在平面直角坐标系中,点M的坐标为(3,4),点N的坐标为(6,0),将△OMN绕点O按逆时针方向旋转得到△OM′N′.若点M′恰好落在x轴上,则点N′的坐标为( )
A. (-3,5) B. (-,)
C. (-4,5) D. (-,)
二、 填空题(每小题3分,共30分)
9. (2025南通海安月考)已知点P在第二象限,且到x轴的距离为2,到y轴的距离为4,则点P的坐标为________.
10. (2025盐城射阳月考)若点A(-2,m)在x轴上,则点B(m+1,2-m)在第________象限.
11. (2024辽宁)在平面直角坐标系中,线段AB的端点坐标分别为A(2,-1),B(1,0),将线段AB平移后,点A的对应点A′的坐标为(2,1),则点B的对应点B′的坐标为________.
12. (2025南京玄武期中)扎染是一种民间传统染色工艺.如图是使用扎染工艺制作的手帕图案,将该图案放在如图所示的平面直角坐标系中,若点A(-3,)与点B关于原点对称,则点B的坐标为________.
(第12题) (第13题) (第15题)
13. (2025盐城大丰月考)如图,已知点P的坐标为(2,3),将线段OP绕点O顺时针旋转90°,则点P的对应点P′的坐标为________.
14. (2025扬州期末)已知点P(m,3),Q(-2m+1,3),且P,Q两点不重合,线段PQ的长度随m的增大而减小,则m的取值范围是________.
15. (2024甘孜州)如图,在一个平面区域内,一台雷达探测器测得在点A,B,C处有目标出现.按某种规则,点A,B的位置可以分别表示为(1,90°),(2,240°),则点C的位置可以表示为________.
16. (2025南通海安月考)在平面直角坐标系中,给出如下定义:点P到x轴,y轴的距离的较小值称为点P的“短距”;当点Q到x轴,y轴的距离相等时,则称点Q为“完美点”.若点C(9-2b,-5)是“完美点”,则点D(-6,2b-1)的“短距”为________.
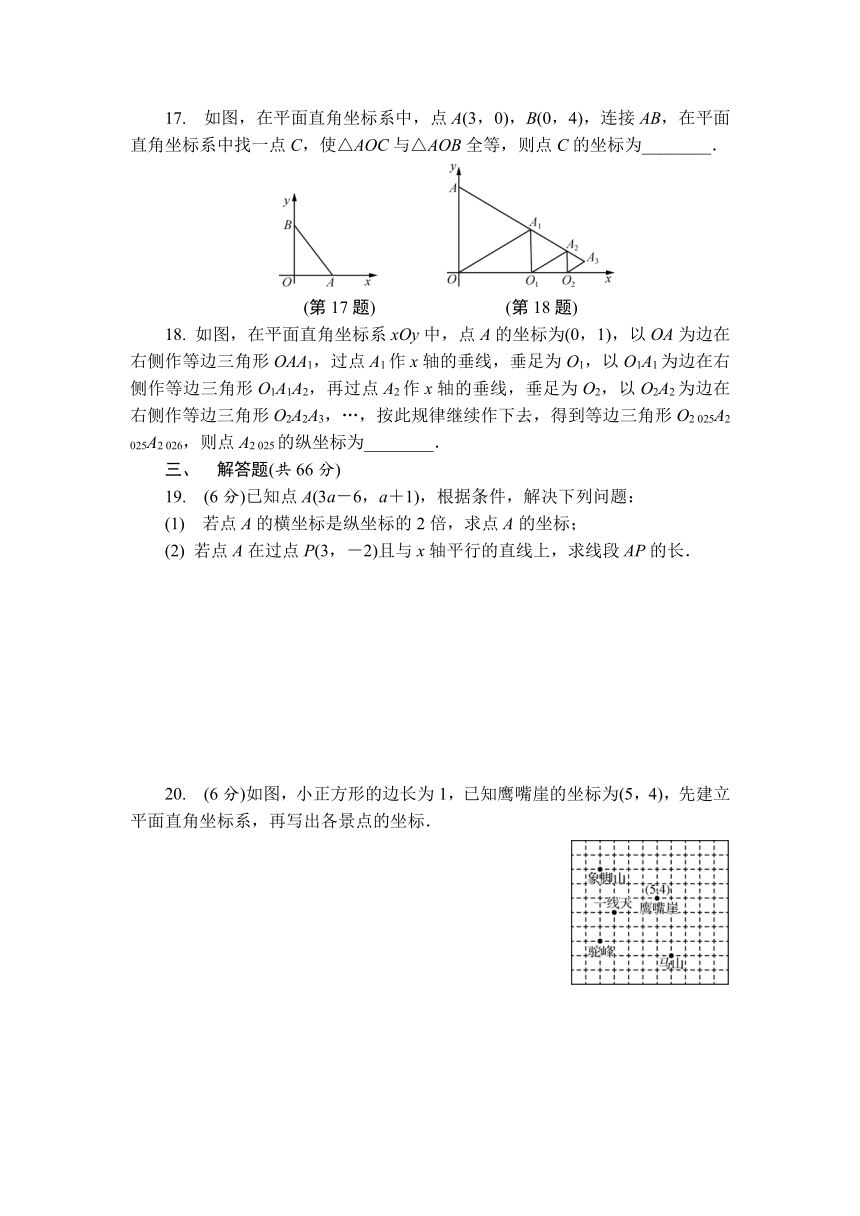
17. 如图,在平面直角坐标系中,点A(3,0),B(0,4),连接AB,在平面直角坐标系中找一点C,使△AOC与△AOB全等,则点C的坐标为________.
(第17题) (第18题)
18. 如图,在平面直角坐标系xOy中,点A的坐标为(0,1),以OA为边在右侧作等边三角形OAA1,过点A1作x轴的垂线,垂足为O1,以O1A1为边在右侧作等边三角形O1A1A2,再过点A2作x轴的垂线,垂足为O2,以O2A2为边在右侧作等边三角形O2A2A3,…,按此规律继续作下去,得到等边三角形O2 025A2 025A2 026,则点A2 025的纵坐标为________.
三、 解答题(共66分)
19. (6分)已知点A(3a-6,a+1),根据条件,解决下列问题:
(1) 若点A的横坐标是纵坐标的2倍,求点A的坐标;
(2) 若点A在过点P(3,-2)且与x轴平行的直线上,求线段AP的长.
20. (6分)如图,小正方形的边长为1,已知鹰嘴崖的坐标为(5,4),先建立平面直角坐标系,再写出各景点的坐标.
21. (8分)在平面直角坐标系中,已知△ABC的边AB在x轴上,且AB=3,点A的坐标为(-2,0),点C的坐标为(2,4).
(1) 找出符合条件的△ABC,写出点B的坐标;
(2) 求△ABC的面积.
22. (8分)如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别是A(-2,3),B(-4,-1),C(-1,1),将△ABC平移,使点B与点O重合,得到△A1OC1,点A,C的对应点分别为A1,C1.
(1) 画出△A1OC1并写出点A1,C1的坐标;
(2) 若直线l经过点(2,0)且与x轴垂直,则直线l也会经过点________(填“A”“C”“A1”或“C1”);
(3) 在(2)的条件下,若点P在直线l上,且△A1OP的面积等于1,直接写出点P的坐标.
23. (8分)在平面直角坐标系中,已知线段AB,其中A(1,-3),B(3,0),平移线段AB到线段CD,使点A的对应点为D,点B的对应点为C.
(1) 若点C的坐标为(-2,4),则点D的坐标是________;
(2) 若点C在y轴的正半轴上,点D在第三象限,且四边形ABCD的面积为14,求点C的坐标.
备用图
24. (8分)如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为坐标原点,点A在x轴的负半轴上,点C在y轴的正半轴上,OA=5,OC=4,在边OC上取一点D,将纸片沿AD翻折,使点O落在边BC上的点E处,求D,E两点的坐标.
25. (10分)在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“近似距离”,给出如下定义:若|x1-x2|≥|y1-y2|,则点P1(x1,y1)与点P2(x2,y2)的“近似距离”为|x1-x2|;若|x1-x2|<|y1-y2|,则点P1(x1,y1)与点P2(x2,y2)的“近似距离”为|y1-y2|.
(1) 已知点P(-3,5),点Q(1,0),求点P与点Q的“近似距离”;
(2) 已知点A(0,-2),B为x轴上的动点.
①若点A与点B的“近似距离”为4,试求出满足条件的点B的坐标;
②直接写出点A与点B的“近似距离”的最小值为 .
26. (12分)在平面直角坐标系xOy中(单位长度为1 cm),已知点M (m,0),N (n,0),且+|2m+n|=0.
(1) 求m,n的值;
(2) 若E是第一象限内一点,且EN⊥x轴,点E到x轴的距离为4,过点E作x轴的平行线a,与y轴交于点A. 点P从点E 处出发,以2 cm/s的速度沿直线a向左移动,点Q从原点O同时出发,以1 cm/s的速度沿x轴向右移动.
①经过几秒,PQ平行于y轴?
②若某一时刻以A,O,Q,P为顶点的四边形的面积是10 cm2,求此时点P的坐标.
第4章平面直角坐标系 达标检测卷
1. A 2. C 3. A 4. A 5. C 6. C 7. D 8. D
9. (-4,2) 10. 一 11. (1,2) 12. (3,-)
13. (3,-2) 14. m< 15. (3,30°) 16. 3或6
17. (0,-4)或(3,4)或(3,-4) 18. ()2 025
19. 解:(1) 因为点A(3a-6,a+1)的横坐标是纵坐标的2倍,
所以3a-6=2(a+1),解得a=8,
所以3a-6=18,a+1=9,
所以点A的坐标为(18,9).
(2) 因为点A在与x轴平行,且过点P(3,-2)的直线上,
所以a+1=-2,解得a=-3,
所以3a-6=-15,
所以点A的坐标为(-15,-2),
所以AP=3-(-15)=18.
20. 解:建立平面直角坐标系略.
驼峰(1,1),马山(6,0),一线天(2,3),象脚山(1,6).
21. 解:(1) 点B的坐标为(-5,0)或(1,0).
(2) △ABC的面积为×3×4=6.
22. 解:(1) 如图,△A1OC1即为所求.A1(2,4),C1(3,2).
(2) A1
(3) 点P的坐标为(2,3)或(2,5).
23. 解:(1) (-4,1)
(2) 如图,设点C(0,m),则点D(-2,m-3).
根据题意,得(m+3)×5-2××3×m-2××2×3=14,解得m=,
所以点C的坐标为(0,).
24. 解:由题意知,折痕AD是四边形OAED的对称轴,
所以DE=OD,AE=AO=5,AB=OC=4,
所以BE===3,
所以CE=5-3=2,所以点E的坐标为(-2,4).
在Rt△DCE中,DC2+CE2=DE2.
因为DE=OD,所以(4-OD)2+22=OD2,
解得OD=2.5,所以点D的坐标为(0,2.5).
综上所述,点D的坐标为(0,2.5),点E的坐标为(-2,4).
25. 解:(1) 因为点P(-3,5),点Q(1,0),|-3-1|<|5-0|=5,
所以点P与点Q的“近似距离”为5.
(2) ①因为B为x轴上的一个动点,
所以设点B的坐标为(x,0).
因为A,B两点的“近似距离”为4,点A(0,-2),
所以|0-x|=4,|-2-0|=2,
解得x=4或x=-4,
所以点B的坐标是(4,0)或(-4,0).
②2
26. 解:(1) 根据题意,得
解得
(2) ①设经过x s,PQ平行于y轴,
根据题意,得6-2x=x,解得x=2.
故经过2 s PQ平行于y轴.
②设经过t s,以A,O,Q,P为顶点的四边形的面积是10 cm2.
当点P在y轴右侧时,
根据题意,得×4=10,
解得t=1,
此时点P 的坐标为(4,4);
当点P在y轴左侧时,
根据题意,得×4=10,
解得t=,
此时点P 的坐标为(-,4).
综上所述,点P的坐标为(4,4)或(-,4).
(时间:100分钟 满分:120分)
一、 选择题(每小题3分,共24分)
1. (2025常州天宁月考)在平面直角坐标系中,点A(2,-4)到x轴的距离是( )
A. 4 B. 2 C. -4 D. -2
2. (2025南京期中)在平面直角坐标系中,点P(0,1)关于点A(1,0)对称的点的坐标为( )
A. (0,-1) B. (1,-1) C. (2,-1) D. (3,-1)
3. (2025南通海安月考)在平面直角坐标系中,将点A(m,2)先向右平移1个单位长度,再向上平移3个单位长度得到点B.若点B的横坐标和纵坐标相等,则m等于( )
A. 4 B. 5 C. 6 D. 7
4. (2024贵州)为培养青少年的科学态度和科学思维,某校创建了“科技创新”社团.小红将“科”“技”“创”“新”写在如图所示的方格纸中,若建立平面直角坐标系,使“创”“新”的坐标分别为(-2,0),(0,0),则“技”所在的象限为( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
(第4题) (第5题) (第6题) (第8题)
5. 如图,平面直角坐标系上有P,Q两点,其坐标分别为P(4,a),Q(b,6).根据图中P,Q两点的位置,判断点(-b,a-7)所在的象限为( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
6. (2025盐城射阳月考)如图,已知点A(1,3),B(4,1),将线段AB绕点M逆时针旋转到A′B′,点A与A′是对应点,点B与B′是对应点,则点M的坐标是( )
A. (-1,-2) B. (1,0) C. (-1,1) D. (1,-3)
7. 已知点P的坐标为(1-a,2a+4),且点P到两坐标轴的距离相等,则点P的坐标是( )
A. (2,2) B. (2,-2)
C. (6,-6) D. (2,2)或(6,-6)
8. 如图,在平面直角坐标系中,点M的坐标为(3,4),点N的坐标为(6,0),将△OMN绕点O按逆时针方向旋转得到△OM′N′.若点M′恰好落在x轴上,则点N′的坐标为( )
A. (-3,5) B. (-,)
C. (-4,5) D. (-,)
二、 填空题(每小题3分,共30分)
9. (2025南通海安月考)已知点P在第二象限,且到x轴的距离为2,到y轴的距离为4,则点P的坐标为________.
10. (2025盐城射阳月考)若点A(-2,m)在x轴上,则点B(m+1,2-m)在第________象限.
11. (2024辽宁)在平面直角坐标系中,线段AB的端点坐标分别为A(2,-1),B(1,0),将线段AB平移后,点A的对应点A′的坐标为(2,1),则点B的对应点B′的坐标为________.
12. (2025南京玄武期中)扎染是一种民间传统染色工艺.如图是使用扎染工艺制作的手帕图案,将该图案放在如图所示的平面直角坐标系中,若点A(-3,)与点B关于原点对称,则点B的坐标为________.
(第12题) (第13题) (第15题)
13. (2025盐城大丰月考)如图,已知点P的坐标为(2,3),将线段OP绕点O顺时针旋转90°,则点P的对应点P′的坐标为________.
14. (2025扬州期末)已知点P(m,3),Q(-2m+1,3),且P,Q两点不重合,线段PQ的长度随m的增大而减小,则m的取值范围是________.
15. (2024甘孜州)如图,在一个平面区域内,一台雷达探测器测得在点A,B,C处有目标出现.按某种规则,点A,B的位置可以分别表示为(1,90°),(2,240°),则点C的位置可以表示为________.
16. (2025南通海安月考)在平面直角坐标系中,给出如下定义:点P到x轴,y轴的距离的较小值称为点P的“短距”;当点Q到x轴,y轴的距离相等时,则称点Q为“完美点”.若点C(9-2b,-5)是“完美点”,则点D(-6,2b-1)的“短距”为________.
17. 如图,在平面直角坐标系中,点A(3,0),B(0,4),连接AB,在平面直角坐标系中找一点C,使△AOC与△AOB全等,则点C的坐标为________.
(第17题) (第18题)
18. 如图,在平面直角坐标系xOy中,点A的坐标为(0,1),以OA为边在右侧作等边三角形OAA1,过点A1作x轴的垂线,垂足为O1,以O1A1为边在右侧作等边三角形O1A1A2,再过点A2作x轴的垂线,垂足为O2,以O2A2为边在右侧作等边三角形O2A2A3,…,按此规律继续作下去,得到等边三角形O2 025A2 025A2 026,则点A2 025的纵坐标为________.
三、 解答题(共66分)
19. (6分)已知点A(3a-6,a+1),根据条件,解决下列问题:
(1) 若点A的横坐标是纵坐标的2倍,求点A的坐标;
(2) 若点A在过点P(3,-2)且与x轴平行的直线上,求线段AP的长.
20. (6分)如图,小正方形的边长为1,已知鹰嘴崖的坐标为(5,4),先建立平面直角坐标系,再写出各景点的坐标.
21. (8分)在平面直角坐标系中,已知△ABC的边AB在x轴上,且AB=3,点A的坐标为(-2,0),点C的坐标为(2,4).
(1) 找出符合条件的△ABC,写出点B的坐标;
(2) 求△ABC的面积.
22. (8分)如图,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别是A(-2,3),B(-4,-1),C(-1,1),将△ABC平移,使点B与点O重合,得到△A1OC1,点A,C的对应点分别为A1,C1.
(1) 画出△A1OC1并写出点A1,C1的坐标;
(2) 若直线l经过点(2,0)且与x轴垂直,则直线l也会经过点________(填“A”“C”“A1”或“C1”);
(3) 在(2)的条件下,若点P在直线l上,且△A1OP的面积等于1,直接写出点P的坐标.
23. (8分)在平面直角坐标系中,已知线段AB,其中A(1,-3),B(3,0),平移线段AB到线段CD,使点A的对应点为D,点B的对应点为C.
(1) 若点C的坐标为(-2,4),则点D的坐标是________;
(2) 若点C在y轴的正半轴上,点D在第三象限,且四边形ABCD的面积为14,求点C的坐标.
备用图
24. (8分)如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为坐标原点,点A在x轴的负半轴上,点C在y轴的正半轴上,OA=5,OC=4,在边OC上取一点D,将纸片沿AD翻折,使点O落在边BC上的点E处,求D,E两点的坐标.
25. (10分)在平面直角坐标系xOy中,对于任意两点P1(x1,y1)与P2(x2,y2)的“近似距离”,给出如下定义:若|x1-x2|≥|y1-y2|,则点P1(x1,y1)与点P2(x2,y2)的“近似距离”为|x1-x2|;若|x1-x2|<|y1-y2|,则点P1(x1,y1)与点P2(x2,y2)的“近似距离”为|y1-y2|.
(1) 已知点P(-3,5),点Q(1,0),求点P与点Q的“近似距离”;
(2) 已知点A(0,-2),B为x轴上的动点.
①若点A与点B的“近似距离”为4,试求出满足条件的点B的坐标;
②直接写出点A与点B的“近似距离”的最小值为 .
26. (12分)在平面直角坐标系xOy中(单位长度为1 cm),已知点M (m,0),N (n,0),且+|2m+n|=0.
(1) 求m,n的值;
(2) 若E是第一象限内一点,且EN⊥x轴,点E到x轴的距离为4,过点E作x轴的平行线a,与y轴交于点A. 点P从点E 处出发,以2 cm/s的速度沿直线a向左移动,点Q从原点O同时出发,以1 cm/s的速度沿x轴向右移动.
①经过几秒,PQ平行于y轴?
②若某一时刻以A,O,Q,P为顶点的四边形的面积是10 cm2,求此时点P的坐标.
第4章平面直角坐标系 达标检测卷
1. A 2. C 3. A 4. A 5. C 6. C 7. D 8. D
9. (-4,2) 10. 一 11. (1,2) 12. (3,-)
13. (3,-2) 14. m< 15. (3,30°) 16. 3或6
17. (0,-4)或(3,4)或(3,-4) 18. ()2 025
19. 解:(1) 因为点A(3a-6,a+1)的横坐标是纵坐标的2倍,
所以3a-6=2(a+1),解得a=8,
所以3a-6=18,a+1=9,
所以点A的坐标为(18,9).
(2) 因为点A在与x轴平行,且过点P(3,-2)的直线上,
所以a+1=-2,解得a=-3,
所以3a-6=-15,
所以点A的坐标为(-15,-2),
所以AP=3-(-15)=18.
20. 解:建立平面直角坐标系略.
驼峰(1,1),马山(6,0),一线天(2,3),象脚山(1,6).
21. 解:(1) 点B的坐标为(-5,0)或(1,0).
(2) △ABC的面积为×3×4=6.
22. 解:(1) 如图,△A1OC1即为所求.A1(2,4),C1(3,2).
(2) A1
(3) 点P的坐标为(2,3)或(2,5).
23. 解:(1) (-4,1)
(2) 如图,设点C(0,m),则点D(-2,m-3).
根据题意,得(m+3)×5-2××3×m-2××2×3=14,解得m=,
所以点C的坐标为(0,).
24. 解:由题意知,折痕AD是四边形OAED的对称轴,
所以DE=OD,AE=AO=5,AB=OC=4,
所以BE===3,
所以CE=5-3=2,所以点E的坐标为(-2,4).
在Rt△DCE中,DC2+CE2=DE2.
因为DE=OD,所以(4-OD)2+22=OD2,
解得OD=2.5,所以点D的坐标为(0,2.5).
综上所述,点D的坐标为(0,2.5),点E的坐标为(-2,4).
25. 解:(1) 因为点P(-3,5),点Q(1,0),|-3-1|<|5-0|=5,
所以点P与点Q的“近似距离”为5.
(2) ①因为B为x轴上的一个动点,
所以设点B的坐标为(x,0).
因为A,B两点的“近似距离”为4,点A(0,-2),
所以|0-x|=4,|-2-0|=2,
解得x=4或x=-4,
所以点B的坐标是(4,0)或(-4,0).
②2
26. 解:(1) 根据题意,得
解得
(2) ①设经过x s,PQ平行于y轴,
根据题意,得6-2x=x,解得x=2.
故经过2 s PQ平行于y轴.
②设经过t s,以A,O,Q,P为顶点的四边形的面积是10 cm2.
当点P在y轴右侧时,
根据题意,得×4=10,
解得t=1,
此时点P 的坐标为(4,4);
当点P在y轴左侧时,
根据题意,得×4=10,
解得t=,
此时点P 的坐标为(-,4).
综上所述,点P的坐标为(4,4)或(-,4).
同课章节目录
