第5章 一次函数 达标检测卷 同步练(含答案) 2025-2026学年数学苏科版(2024)八年级上册
文档属性
| 名称 | 第5章 一次函数 达标检测卷 同步练(含答案) 2025-2026学年数学苏科版(2024)八年级上册 | 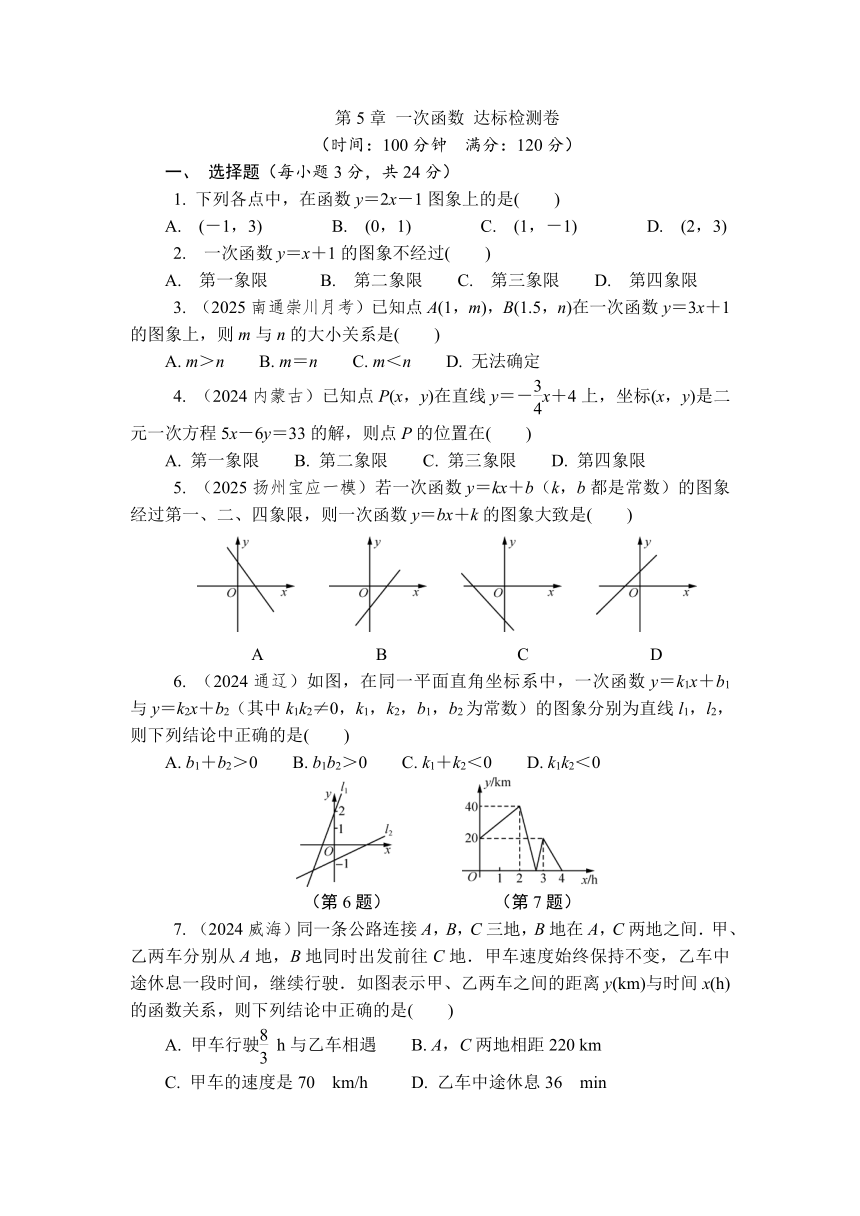 | |
| 格式 | docx | ||
| 文件大小 | 227.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 15:18:01 | ||
图片预览




文档简介
第5章 一次函数 达标检测卷
(时间:100分钟 满分:120分)
一、 选择题(每小题3分,共24分)
1. 下列各点中,在函数y=2x-1图象上的是( )
A. (-1,3) B. (0,1) C. (1,-1) D. (2,3)
2. 一次函数y=x+1的图象不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. (2025南通崇川月考)已知点A(1,m),B(1.5,n)在一次函数y=3x+1的图象上,则m与n的大小关系是( )
A. m>n B. m=n C. m<n D. 无法确定
4. (2024内蒙古)已知点P(x,y)在直线y=-x+4上,坐标(x,y)是二元一次方程5x-6y=33的解,则点P的位置在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
5. (2025扬州宝应一模)若一次函数y=kx+b(k,b都是常数)的图象经过第一、二、四象限,则一次函数y=bx+k的图象大致是( )
A B C D
6. (2024通辽)如图,在同一平面直角坐标系中,一次函数y=k1x+b1与y=k2x+b2(其中k1k2≠0,k1,k2,b1,b2为常数)的图象分别为直线l1,l2,则下列结论中正确的是( )
A. b1+b2>0 B. b1b2>0 C. k1+k2<0 D. k1k2<0
(第6题) (第7题)
7. (2024威海)同一条公路连接A,B,C三地,B地在A,C两地之间.甲、乙两车分别从A地,B地同时出发前往C地.甲车速度始终保持不变,乙车中途休息一段时间,继续行驶.如图表示甲、乙两车之间的距离y(km)与时间x(h)的函数关系,则下列结论中正确的是( )
A. 甲车行驶 h与乙车相遇 B. A,C两地相距220 km
C. 甲车的速度是70 km/h D. 乙车中途休息36 min
8. 若一次函数y=x+5的图象经过点A(a,b),B(c,d),则a(c-d)+b(d-c)等于( )
A. 0 B. 20
C. 25 D. -25
二、 填空题(每小题3分,共30分)
9. 若函数y=kx+3的图象经过点(2,5),则k= .
10. 若将直线y=-2x向上平移4个单位长度,则平移后的直线的函数表达式是 .
11. (2024宁夏)在平面直角坐标系中,已知一条直线与两坐标轴围成的三角形是等腰三角形,则该直线的表达式可能为 .(写出一个即可)
12. 已知关于x的一次函数y=(2a+1)x+a-2,若y随x的增大而增大,且其图象与y轴的交点在原点下方,则实数a的取值范围是 .
13. (2024徐州九里期末)如图,直线y=2x与y=kx+b相交于点P(1,2),则关于x的方程kx+b=2x的解是 .
(第13题) (第16题) (第17题) (第18题)
14. (2025南京鼓楼月考)已知一次函数y=mx-4m,当1≤x≤3时,2≤y≤6,则m的值为 .
15. (2024南通)在平面直角坐标系xOy中,已知点A(3,0),B(0,3),直线y=kx+b(k,b为常数,且k>0)经过点(1,0),并把△AOB分成两部分,其中靠近原点部分的面积为,则k的值为 .
16. 如图,一次函数y=-2x+4的图象与坐标轴分别交于A,B两点,将线段AB绕点A按逆时针方向旋转90°,点B落在点B′处,则点B′的坐标是 .
17. 如图,在平面直角坐标系中,一次函数y=k(x-1)的图象分别交x轴,y轴于A,B两点,且OB=2OA,将直线AB绕点B按顺时针方向旋转45°,交x轴于点C,则直线BC的函数表达式是 .
18. 如图,在平面直角坐标系xOy中,点B的坐标为(-8,6),过点B分别作x轴,y轴的垂线,垂足分别为C,A,直线y=-2x-6与AB交于点D,与y轴交于点E,动点M在线段BC上,动点N在直线y=-2x-6上.若△AMN是以N为直角顶点的等腰直角三角形,则点M的坐标为 .
三、 解答题(共66分)
19. (6分)已知y-2与2x+3成正比例,且当x=1时,y=12.
(1) 求y与x的函数表达式;
(2) 当y=4时,求x的值.
20. (6分)(2025南京模拟)在同一平面直角坐标系中,关于x轴对称的两点P,Q分别在一次函数y=-x+3与y=3x-5的图象上,求点P的坐标.
21. (6分)如图,已知直线l:y=-x+4与x轴,y轴分别交于A,B两点,x轴上一点C的坐标为(6,0),P是直线l上的一点.
(1) 当点P的横坐标为2时,求△COP的面积;
(2) 若S△COP=S△AOB,求此时点P的坐标.
22. (8分)(2025淮安期末)如图,在平面直角坐标系中,一次函数y=x+2的图象与x轴交于点A,与y轴交于点B,且与正比例函数y=x的图象交于点C.
(1) 点B的坐标为 ;
(2) 求△BOC的面积;
(3) 在y轴上求一点P,使△POC是以OC为腰的等腰三角形.请直接写出所有符合条件的点P的坐标.
23. (8分)(2025无锡锡山月考)某校计划采购凳子,商场有A,B两种型号的凳子出售,并规定:对于A型凳子,采购数量若超过250张,则超出部分可在原价基础上每张优惠a元;B型凳子的售价为40元/张.学校经测算,若购买300张A型凳子需要花费14 250元;若购买500张A型凳子需要花费21 250元.
(1) 求a的值;
(2) 学校要采购A,B两种型号凳子共900张,购买A型凳子不少于150张,且不超过B型凳子数量的2倍,请通过计算帮学校决策如何分配购买数量可以使得总采购费用最少?最少是多少元?
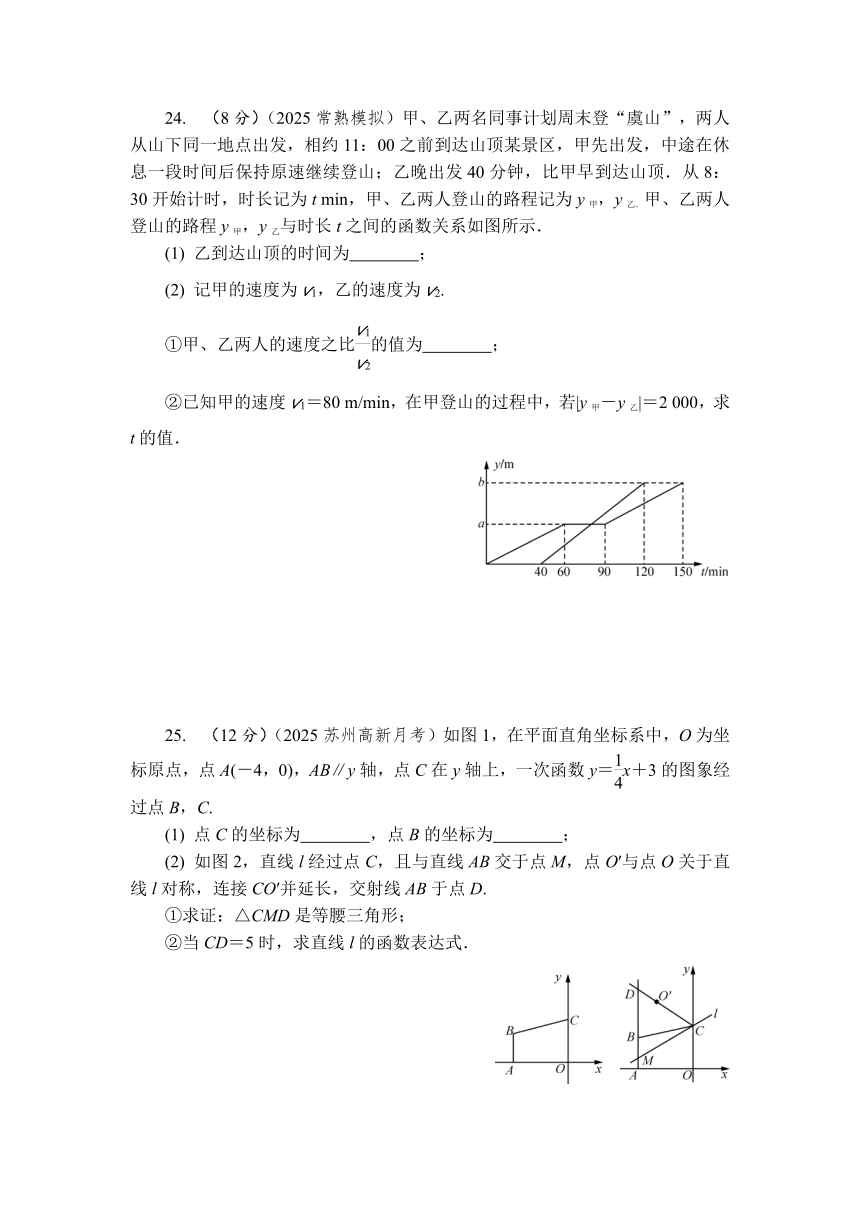
24. (8分)(2025常熟模拟)甲、乙两名同事计划周末登“虞山”,两人从山下同一地点出发,相约11:00之前到达山顶某景区,甲先出发,中途在休息一段时间后保持原速继续登山;乙晚出发40分钟,比甲早到达山顶.从8:30开始计时,时长记为t min,甲、乙两人登山的路程记为y甲,y乙.甲、乙两人登山的路程y甲,y乙与时长t之间的函数关系如图所示.
(1) 乙到达山顶的时间为 ;
(2) 记甲的速度为v1,乙的速度为v2.
①甲、乙两人的速度之比的值为 ;
②已知甲的速度v1=80 m/min,在甲登山的过程中,若|y甲-y乙|=2 000,求t的值.
25. (12分)(2025苏州高新月考)如图1,在平面直角坐标系中,O为坐标原点,点A(-4,0),AB∥y轴,点C在y轴上,一次函数y=x+3的图象经过点B,C.
(1) 点C的坐标为 ,点B的坐标为 ;
(2) 如图2,直线l经过点C,且与直线AB交于点M,点O′与点O关于直线l对称,连接CO′并延长,交射线AB于点D.
①求证:△CMD是等腰三角形;
②当CD=5时,求直线l的函数表达式.
图1 图2
26. (12分)(2025南京玄武月考)如图1,在平面直角坐标系中,一次函数y=-x+4与x轴交于点B,与y轴交于点A,C为线段AB的中点,过点C作CD⊥x轴,垂足为D.
(1) 若在直线AB上有一点M,使得△OBM的面积为9,求点M的坐标;
(2) 如图2,若E为y轴负半轴上一点,连接CE交x轴于点F,且CF=FE,在直线CD上有一点P,使得AP+EP最小,求点P的坐标;
(3) 如图3,若直线CD上存在点Q使得∠ABQ=45°,请直接写出点Q的坐标.
图1 图2 图3
第5章 一次函数 达标检测卷
1. D 2. D 3. C 4. D 5. B 6. A 7. A 8. C
9. 1 10. y=-2x+4 11. y=x+1(答案不唯一)
12. -17. y=x-2 18. (-8,6)或(-8,)
19. 解:(1) 设y-2=k(2x+3),
将x=1,y=12代入,得12-2=5k,解得k=2,
所以y-2=2(2x+3),
所以y与x的函数表达式为y=4x+8.
(2) 当y=4时,4x+8=4,
解得x=-1.
20. 解:设点P的横坐标为a,则点Q的横坐标为a.
因为点P在一次函数y=-x+3的图象上,
所以点P(a,-a+3).
因为点Q在一次函数y=3x-5的图象上,
所以点Q(a,3a-5),
所以-a+3+3a-5=0,
解得a=1,
所以点P的坐标为(1,2).
21. 解:(1) 将x=2代入y=-x+4中,
得y=-1+4=3,
所以点P的坐标为(2,3),
所以S△COP=OC·yP=×6×3=9.
(2) 将x=0代入y=-x+4中,得y=4,
所以点B的坐标为(0,4).
将y=0代入y=-x+4中,得0=-x+4,
解得x=8,
所以点A的坐标为(8,0),
所以S△AOB=OA·OB=×8×4=16.
设点P的坐标为(m,-m+4),
则S△COP=OC·|yP|=×6×=S△AOB=16×=6,
解得m=4或m=12,
所以点P的坐标为(4,2)或(12,-2).
22. 解:(1) (0,2)
(2) 联立两个函数表达式,得x+2=x,解得x=3,则点C的坐标为(3,4),
所以S△BOC=OB·xC=×2×3=3.
(3) 设点P的坐标为(0,y).
由点P,O,C的坐标,得PO2=y2,PC2=9+(y-4)2,CO2=25,
则PO=CO或PC=OC,
即25=9+(y-4)2或y2=25,解得y=±5或y=0(舍去)或y=8,
所以点P的坐标为(0,5)或(0,-5)或(0,8).
23. 解:(1) 设A型凳子的售价为x元/张.
根据题意,得
解得
所以a的值为15.
(2) 设购买A型凳子m张,则购买B型凳子(900-m)张.
根据题意,得
解得150≤m≤600.
设总采购费用为w元,
当150≤m≤250时,w=50m+40(900-m)=10m+36 000.
因为10>0,所以w随m的增大而增大,所以当m=150时,w的最小值为37 500;
当250<m≤600时,w=50×250+(50-15)×(m-250)+40(900-m)=-5m+39 750.
因为-5<0,所以w随m的增大而减小,所以当m=600时,w的最小值为36 750.
因为37 500>36 750,
所以当购买A型凳子600张,购买B型凳子300张时,总采购费用最少,最少是36 750元.
24. 解:(1) 10:30
(2) ①
②根据题意,得a=60×80=4 800,v2==×80=120(m/min),
则y乙=120(t-40)=120t-4 800(40≤t≤120),
易得当0≤t≤60时,y甲=80t,所以|y甲-y乙|=80t-(120t-4 800)=2 000,解得t=70,舍去;
当60<t≤90时,y甲=4 800,所以|y甲-y乙|=|4 800-(120t-4 800)|=2 000,解得t=或t=(舍去);
当90<t≤120时,y甲=4 800+80(t-90)=80t-2 400,
所以|y甲-y乙|=120t-4 800-(80t-2 400)=2 000,
解得t=110;
当120所以|y甲-y乙|=9 600-(80t-2 400)=2 000,
解得t=125.
综上,t的值为或110或125.
25. (1)解:(0,3) (-4,2)
(2) ①证明:因为AB∥y轴,
所以∠OCM=∠CMD.
因为∠OCM=∠MCD,
所以∠CMD=∠MCD,
所以MD=CD,
所以△CMD是等腰三角形.
②解:如图,过点D作DP⊥y轴于点P.
在Rt△DCP中,由勾股定理,得CP==3,
所以OP=AD=CO+CP=3+3=6,
所以AM=AD-DM=6-5=1,
所以点M的坐标是(-4,1).
设直线l的函数表达式为y=kx+b(k≠0),
将点M(-4,1),C(0,3)分别代入,得
解得,
所以直线l的函数表达式为y=x+3;
当点D与点A重合时,直线l的函数表达式为y=2x+3.
综上,直线l的函数表达式为y=x+3或y=2x+3.
26. 解:(1) 令y=-x+4=0,
解得x=6,
令x=0,得y=4,
所以点A的坐标为(0,4),点B的坐标为(6,0).
设点M的纵坐标为yM,根据题意,得OB·|yM|=9,
即×6×|yM|=9,
解得yM=3或yM=-3,
将y=3代入y=-x+4中,得3=-x+4,
解得x=,
所以此时点M的坐标为(,3);
将y=-3代入y=-x+4中,得-3=-x+4,
解得x=,
所以此时点M的坐标为(,-3).
综上,点M的坐标为(,3)或(,-3).
(2) 因为C为线段AB的中点,
所以点C的坐标为(3,2).
因为CD⊥x轴,
所以CD=2.
在△CFD和△EFO中,
所以△CFD≌△EFO(AAS),
所以EO=CD=2,
所以点E的坐标为(0,-2).
作点A关于直线CD的对称点A′(6,4),连接A′E交CD于点P,连接AP,如图1,
根据轴对称可知AP=A′P,
所以AP+EP=A′P+EP,
所以当A′P+EP最小时,AP+EP最小.
因为两点之间线段最短,
所以此时P为所求点.
设直线A′E的函数表达式为y=kx+b,将点A′(6,4),E(0,-2)代入,得
解得
所以直线A′E的函数表达式为y=x-2,
当x=3时,y=x-2=1,
所以点P的坐标为(3,1).
(3) 当点Q在AB的上方时,如图2,过点A作AM⊥AB交BQ于点M,过点M作MH⊥y轴于点H,
则∠BAM=90°.
因为∠ABQ=45°,
所以△ABM为等腰直角三角形,
所以AM=AB.
因为∠HMA+∠HAM=90°,∠HAM+∠OAB=90°,
所以∠HMA=∠OAB.
在△AHM和△AOB中,
所以△AHM≌△BOA(AAS),
所以AH=BO=6,HM=OA=4,
所以点M的坐标为(4,10).
设直线BM的函数表达式为y=kx+b,将点M(4,10),B(6,0)代入,得
解得
所以直线BM的函数表达式为y=-5x+30,
当x=3时,y=-5x+30=15,
所以点Q的坐标为(3,15);
当点Q在AB的下方时,
过点A作AN⊥AB交BQ于点N,
则∠NAB=90°,
所以∠MAB+∠NAB=180°,
所以N,A,M三点共线.
因为∠ABN=45°,
所以△ABN为等腰直角三角形,
所以AN=AB,
所以AN=AM,
所以A为MN的中点.
由中点坐标公式,得点N(0-4,2×4-10),即点N(-4,-2).
易得直线BN的函数表达式为y=x-,
当x=3时,y=x-=-,
所以点Q的坐标为(3,-).
综上,点Q的坐标为(3,-)或(3,15).
图1 图2
(时间:100分钟 满分:120分)
一、 选择题(每小题3分,共24分)
1. 下列各点中,在函数y=2x-1图象上的是( )
A. (-1,3) B. (0,1) C. (1,-1) D. (2,3)
2. 一次函数y=x+1的图象不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. (2025南通崇川月考)已知点A(1,m),B(1.5,n)在一次函数y=3x+1的图象上,则m与n的大小关系是( )
A. m>n B. m=n C. m<n D. 无法确定
4. (2024内蒙古)已知点P(x,y)在直线y=-x+4上,坐标(x,y)是二元一次方程5x-6y=33的解,则点P的位置在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
5. (2025扬州宝应一模)若一次函数y=kx+b(k,b都是常数)的图象经过第一、二、四象限,则一次函数y=bx+k的图象大致是( )
A B C D
6. (2024通辽)如图,在同一平面直角坐标系中,一次函数y=k1x+b1与y=k2x+b2(其中k1k2≠0,k1,k2,b1,b2为常数)的图象分别为直线l1,l2,则下列结论中正确的是( )
A. b1+b2>0 B. b1b2>0 C. k1+k2<0 D. k1k2<0
(第6题) (第7题)
7. (2024威海)同一条公路连接A,B,C三地,B地在A,C两地之间.甲、乙两车分别从A地,B地同时出发前往C地.甲车速度始终保持不变,乙车中途休息一段时间,继续行驶.如图表示甲、乙两车之间的距离y(km)与时间x(h)的函数关系,则下列结论中正确的是( )
A. 甲车行驶 h与乙车相遇 B. A,C两地相距220 km
C. 甲车的速度是70 km/h D. 乙车中途休息36 min
8. 若一次函数y=x+5的图象经过点A(a,b),B(c,d),则a(c-d)+b(d-c)等于( )
A. 0 B. 20
C. 25 D. -25
二、 填空题(每小题3分,共30分)
9. 若函数y=kx+3的图象经过点(2,5),则k= .
10. 若将直线y=-2x向上平移4个单位长度,则平移后的直线的函数表达式是 .
11. (2024宁夏)在平面直角坐标系中,已知一条直线与两坐标轴围成的三角形是等腰三角形,则该直线的表达式可能为 .(写出一个即可)
12. 已知关于x的一次函数y=(2a+1)x+a-2,若y随x的增大而增大,且其图象与y轴的交点在原点下方,则实数a的取值范围是 .
13. (2024徐州九里期末)如图,直线y=2x与y=kx+b相交于点P(1,2),则关于x的方程kx+b=2x的解是 .
(第13题) (第16题) (第17题) (第18题)
14. (2025南京鼓楼月考)已知一次函数y=mx-4m,当1≤x≤3时,2≤y≤6,则m的值为 .
15. (2024南通)在平面直角坐标系xOy中,已知点A(3,0),B(0,3),直线y=kx+b(k,b为常数,且k>0)经过点(1,0),并把△AOB分成两部分,其中靠近原点部分的面积为,则k的值为 .
16. 如图,一次函数y=-2x+4的图象与坐标轴分别交于A,B两点,将线段AB绕点A按逆时针方向旋转90°,点B落在点B′处,则点B′的坐标是 .
17. 如图,在平面直角坐标系中,一次函数y=k(x-1)的图象分别交x轴,y轴于A,B两点,且OB=2OA,将直线AB绕点B按顺时针方向旋转45°,交x轴于点C,则直线BC的函数表达式是 .
18. 如图,在平面直角坐标系xOy中,点B的坐标为(-8,6),过点B分别作x轴,y轴的垂线,垂足分别为C,A,直线y=-2x-6与AB交于点D,与y轴交于点E,动点M在线段BC上,动点N在直线y=-2x-6上.若△AMN是以N为直角顶点的等腰直角三角形,则点M的坐标为 .
三、 解答题(共66分)
19. (6分)已知y-2与2x+3成正比例,且当x=1时,y=12.
(1) 求y与x的函数表达式;
(2) 当y=4时,求x的值.
20. (6分)(2025南京模拟)在同一平面直角坐标系中,关于x轴对称的两点P,Q分别在一次函数y=-x+3与y=3x-5的图象上,求点P的坐标.
21. (6分)如图,已知直线l:y=-x+4与x轴,y轴分别交于A,B两点,x轴上一点C的坐标为(6,0),P是直线l上的一点.
(1) 当点P的横坐标为2时,求△COP的面积;
(2) 若S△COP=S△AOB,求此时点P的坐标.
22. (8分)(2025淮安期末)如图,在平面直角坐标系中,一次函数y=x+2的图象与x轴交于点A,与y轴交于点B,且与正比例函数y=x的图象交于点C.
(1) 点B的坐标为 ;
(2) 求△BOC的面积;
(3) 在y轴上求一点P,使△POC是以OC为腰的等腰三角形.请直接写出所有符合条件的点P的坐标.
23. (8分)(2025无锡锡山月考)某校计划采购凳子,商场有A,B两种型号的凳子出售,并规定:对于A型凳子,采购数量若超过250张,则超出部分可在原价基础上每张优惠a元;B型凳子的售价为40元/张.学校经测算,若购买300张A型凳子需要花费14 250元;若购买500张A型凳子需要花费21 250元.
(1) 求a的值;
(2) 学校要采购A,B两种型号凳子共900张,购买A型凳子不少于150张,且不超过B型凳子数量的2倍,请通过计算帮学校决策如何分配购买数量可以使得总采购费用最少?最少是多少元?
24. (8分)(2025常熟模拟)甲、乙两名同事计划周末登“虞山”,两人从山下同一地点出发,相约11:00之前到达山顶某景区,甲先出发,中途在休息一段时间后保持原速继续登山;乙晚出发40分钟,比甲早到达山顶.从8:30开始计时,时长记为t min,甲、乙两人登山的路程记为y甲,y乙.甲、乙两人登山的路程y甲,y乙与时长t之间的函数关系如图所示.
(1) 乙到达山顶的时间为 ;
(2) 记甲的速度为v1,乙的速度为v2.
①甲、乙两人的速度之比的值为 ;
②已知甲的速度v1=80 m/min,在甲登山的过程中,若|y甲-y乙|=2 000,求t的值.
25. (12分)(2025苏州高新月考)如图1,在平面直角坐标系中,O为坐标原点,点A(-4,0),AB∥y轴,点C在y轴上,一次函数y=x+3的图象经过点B,C.
(1) 点C的坐标为 ,点B的坐标为 ;
(2) 如图2,直线l经过点C,且与直线AB交于点M,点O′与点O关于直线l对称,连接CO′并延长,交射线AB于点D.
①求证:△CMD是等腰三角形;
②当CD=5时,求直线l的函数表达式.
图1 图2
26. (12分)(2025南京玄武月考)如图1,在平面直角坐标系中,一次函数y=-x+4与x轴交于点B,与y轴交于点A,C为线段AB的中点,过点C作CD⊥x轴,垂足为D.
(1) 若在直线AB上有一点M,使得△OBM的面积为9,求点M的坐标;
(2) 如图2,若E为y轴负半轴上一点,连接CE交x轴于点F,且CF=FE,在直线CD上有一点P,使得AP+EP最小,求点P的坐标;
(3) 如图3,若直线CD上存在点Q使得∠ABQ=45°,请直接写出点Q的坐标.
图1 图2 图3
第5章 一次函数 达标检测卷
1. D 2. D 3. C 4. D 5. B 6. A 7. A 8. C
9. 1 10. y=-2x+4 11. y=x+1(答案不唯一)
12. -
19. 解:(1) 设y-2=k(2x+3),
将x=1,y=12代入,得12-2=5k,解得k=2,
所以y-2=2(2x+3),
所以y与x的函数表达式为y=4x+8.
(2) 当y=4时,4x+8=4,
解得x=-1.
20. 解:设点P的横坐标为a,则点Q的横坐标为a.
因为点P在一次函数y=-x+3的图象上,
所以点P(a,-a+3).
因为点Q在一次函数y=3x-5的图象上,
所以点Q(a,3a-5),
所以-a+3+3a-5=0,
解得a=1,
所以点P的坐标为(1,2).
21. 解:(1) 将x=2代入y=-x+4中,
得y=-1+4=3,
所以点P的坐标为(2,3),
所以S△COP=OC·yP=×6×3=9.
(2) 将x=0代入y=-x+4中,得y=4,
所以点B的坐标为(0,4).
将y=0代入y=-x+4中,得0=-x+4,
解得x=8,
所以点A的坐标为(8,0),
所以S△AOB=OA·OB=×8×4=16.
设点P的坐标为(m,-m+4),
则S△COP=OC·|yP|=×6×=S△AOB=16×=6,
解得m=4或m=12,
所以点P的坐标为(4,2)或(12,-2).
22. 解:(1) (0,2)
(2) 联立两个函数表达式,得x+2=x,解得x=3,则点C的坐标为(3,4),
所以S△BOC=OB·xC=×2×3=3.
(3) 设点P的坐标为(0,y).
由点P,O,C的坐标,得PO2=y2,PC2=9+(y-4)2,CO2=25,
则PO=CO或PC=OC,
即25=9+(y-4)2或y2=25,解得y=±5或y=0(舍去)或y=8,
所以点P的坐标为(0,5)或(0,-5)或(0,8).
23. 解:(1) 设A型凳子的售价为x元/张.
根据题意,得
解得
所以a的值为15.
(2) 设购买A型凳子m张,则购买B型凳子(900-m)张.
根据题意,得
解得150≤m≤600.
设总采购费用为w元,
当150≤m≤250时,w=50m+40(900-m)=10m+36 000.
因为10>0,所以w随m的增大而增大,所以当m=150时,w的最小值为37 500;
当250<m≤600时,w=50×250+(50-15)×(m-250)+40(900-m)=-5m+39 750.
因为-5<0,所以w随m的增大而减小,所以当m=600时,w的最小值为36 750.
因为37 500>36 750,
所以当购买A型凳子600张,购买B型凳子300张时,总采购费用最少,最少是36 750元.
24. 解:(1) 10:30
(2) ①
②根据题意,得a=60×80=4 800,v2==×80=120(m/min),
则y乙=120(t-40)=120t-4 800(40≤t≤120),
易得当0≤t≤60时,y甲=80t,所以|y甲-y乙|=80t-(120t-4 800)=2 000,解得t=70,舍去;
当60<t≤90时,y甲=4 800,所以|y甲-y乙|=|4 800-(120t-4 800)|=2 000,解得t=或t=(舍去);
当90<t≤120时,y甲=4 800+80(t-90)=80t-2 400,
所以|y甲-y乙|=120t-4 800-(80t-2 400)=2 000,
解得t=110;
当120
解得t=125.
综上,t的值为或110或125.
25. (1)解:(0,3) (-4,2)
(2) ①证明:因为AB∥y轴,
所以∠OCM=∠CMD.
因为∠OCM=∠MCD,
所以∠CMD=∠MCD,
所以MD=CD,
所以△CMD是等腰三角形.
②解:如图,过点D作DP⊥y轴于点P.
在Rt△DCP中,由勾股定理,得CP==3,
所以OP=AD=CO+CP=3+3=6,
所以AM=AD-DM=6-5=1,
所以点M的坐标是(-4,1).
设直线l的函数表达式为y=kx+b(k≠0),
将点M(-4,1),C(0,3)分别代入,得
解得,
所以直线l的函数表达式为y=x+3;
当点D与点A重合时,直线l的函数表达式为y=2x+3.
综上,直线l的函数表达式为y=x+3或y=2x+3.
26. 解:(1) 令y=-x+4=0,
解得x=6,
令x=0,得y=4,
所以点A的坐标为(0,4),点B的坐标为(6,0).
设点M的纵坐标为yM,根据题意,得OB·|yM|=9,
即×6×|yM|=9,
解得yM=3或yM=-3,
将y=3代入y=-x+4中,得3=-x+4,
解得x=,
所以此时点M的坐标为(,3);
将y=-3代入y=-x+4中,得-3=-x+4,
解得x=,
所以此时点M的坐标为(,-3).
综上,点M的坐标为(,3)或(,-3).
(2) 因为C为线段AB的中点,
所以点C的坐标为(3,2).
因为CD⊥x轴,
所以CD=2.
在△CFD和△EFO中,
所以△CFD≌△EFO(AAS),
所以EO=CD=2,
所以点E的坐标为(0,-2).
作点A关于直线CD的对称点A′(6,4),连接A′E交CD于点P,连接AP,如图1,
根据轴对称可知AP=A′P,
所以AP+EP=A′P+EP,
所以当A′P+EP最小时,AP+EP最小.
因为两点之间线段最短,
所以此时P为所求点.
设直线A′E的函数表达式为y=kx+b,将点A′(6,4),E(0,-2)代入,得
解得
所以直线A′E的函数表达式为y=x-2,
当x=3时,y=x-2=1,
所以点P的坐标为(3,1).
(3) 当点Q在AB的上方时,如图2,过点A作AM⊥AB交BQ于点M,过点M作MH⊥y轴于点H,
则∠BAM=90°.
因为∠ABQ=45°,
所以△ABM为等腰直角三角形,
所以AM=AB.
因为∠HMA+∠HAM=90°,∠HAM+∠OAB=90°,
所以∠HMA=∠OAB.
在△AHM和△AOB中,
所以△AHM≌△BOA(AAS),
所以AH=BO=6,HM=OA=4,
所以点M的坐标为(4,10).
设直线BM的函数表达式为y=kx+b,将点M(4,10),B(6,0)代入,得
解得
所以直线BM的函数表达式为y=-5x+30,
当x=3时,y=-5x+30=15,
所以点Q的坐标为(3,15);
当点Q在AB的下方时,
过点A作AN⊥AB交BQ于点N,
则∠NAB=90°,
所以∠MAB+∠NAB=180°,
所以N,A,M三点共线.
因为∠ABN=45°,
所以△ABN为等腰直角三角形,
所以AN=AB,
所以AN=AM,
所以A为MN的中点.
由中点坐标公式,得点N(0-4,2×4-10),即点N(-4,-2).
易得直线BN的函数表达式为y=x-,
当x=3时,y=x-=-,
所以点Q的坐标为(3,-).
综上,点Q的坐标为(3,-)或(3,15).
图1 图2
同课章节目录
