拉分题型8 函数中的双变量问题 复习练习(含答案)高中数学必修1(苏教版2019)
文档属性
| 名称 | 拉分题型8 函数中的双变量问题 复习练习(含答案)高中数学必修1(苏教版2019) |  | |
| 格式 | doc | ||
| 文件大小 | 499.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 14:17:08 | ||
图片预览

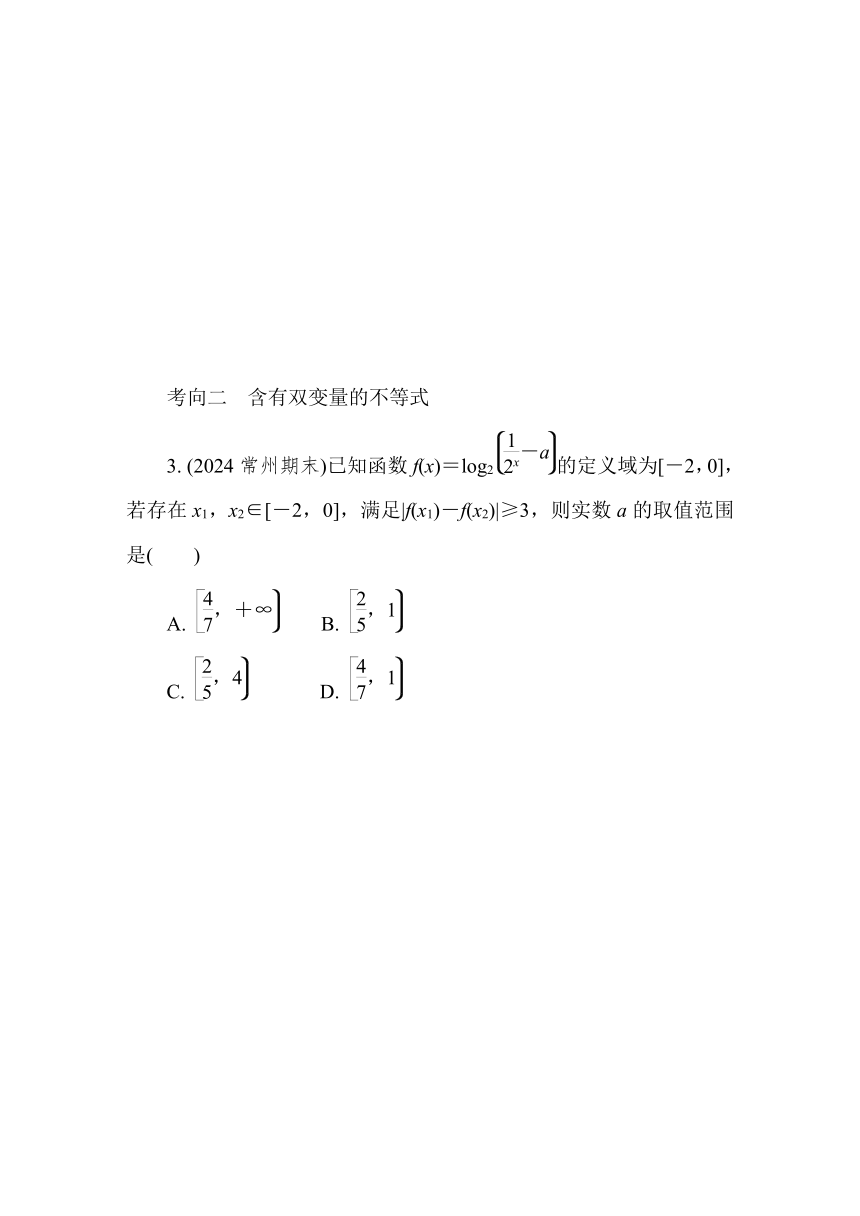


文档简介
eq \o(\s\up7(),\s\do5( 拉分题型8 函数中的双变量问题))
考向一 含有双变量的方程
1. (2024宁波九校期末联考)已知函数f(x)=若对任意x1∈[2,+∞),都存在唯一的x2∈(-∞,2),使得f(x2)=f(x1),则实数m的取值范围是________.
2. (2024南京师大附中期末)已知函数f(x)=x|x|,函数g(x)=x2-2x-m.
(1) 求不等式f(x3-2)>-1的解集;
(2) 若对于任意x2∈[-1,2],都存在x1∈[-2,1],使得g(x2)=f(x1),求实数m的取值范围.
考向二 含有双变量的不等式
3. (2024常州期末)已知函数f(x)=log2的定义域为[-2,0],若存在x1,x2∈[-2,0],满足|f(x1)-f(x2)|≥3,则实数a的取值范围是( )
A. B.
C. D.
4. (2023南通中学阶段考试)已知函数f(x)=.
(1) 求f(-2)+f(2)的值;
(2) 求函数f(x)的值域;
(3) 若g(x)=[f(x)]2-+2a,且对任意的x1,x2∈R,都有|g(x1)-g(x2)|<3,求实数a的取值范围.
5. (2023如皋期中)已知函数f(x)=2-log2x,g(x)=
(1) 求函数g(x)的最大值;
(2) 若对任意x1∈[4,16],x2∈R,不等式f(2kx1)·f(x)>g(x2)恒成立,求实数k的取值范围.
函数中双变量问题大致有以下几种类型:(1) 等式中的双变量问题,一般将同一变量放到同一边,利用函数的值域之间的关系建立不等式(组)求解;(2) 不等式中的双变量问题,一般将同一变量放到同一边,利用函数的最值之间的关系建立不等式(组)求解.
拉分题型8 函数中的双变量问题
1. 设函数f(x)在区间(-∞,2)和[2,+∞)上的值域分别为A,B.当m≤0时,函数y=,y=x-1在区间[2,+∞)上均单调递增,则函数f(x)=x+-1在区间[2,+∞)上单调递增;当0<≤2,即0-2,则2-x>2-2=.当m≤,且x<2时,f(x)=2-x-m>-m,即A=(-m,+∞),此时,函数f(x)=x+-1在区间[2,+∞)上单调递增,则f(x)≥f(2)=1+,即B=[1+,+∞).由题意可知,B A,则1+>-m,解得m>-,所以-0,当-log2m≤x<2时,f(x)=m-2-x∈,如图1所示.若对任意x1∈[2,+∞),都存在唯一的x2∈(-∞,2),使得f(x2)=f(x1),只需+1≥m-,解得m≤,所以4时,>2,函数f(x)=x+-1在区间[2,)上单调递减,在区间(,+∞)上单调递增,则B=[2-1,+∞).当x<2时,f(x)=当x<-log2m时,f(x)=2-x-m>0,当-log2m≤x<2时,f(x)=m-2-x∈,如图2所示. 若对任意x1∈[2,+∞),都存在唯一的x2∈(-∞,2),使得f(x2)=f(x1),只需2-1≥m-,解得≤m≤,与m>4矛盾,所以m不存在.综上,实数m的取值范围是.
图1 图2
利用函数值相等求参数的取值范围,解题的关键在于对参数进行分类讨论,结合图形将题中的信息等价转化为不等式求解.
2. (1) 因为函数f(x)=x|x|的定义域为R,
且f(-x)=-x|-x|=-x|x|=-f(x),
所以函数f(x)为奇函数.
当x∈[0,+∞)时,f(x)=x2,
则f(x)在区间[0,+∞)上单调递增,
所以f(x)是R上的增函数.
又f(-1)=-1,所以不等式f(x3-2)>-1,即f(x3-2)>f(-1),
所以x3-2>-1,解得x>1,
所以不等式f(x3-2)>-1的解集为(1,+∞).
(2) 因为函数g(x)=x2-2x-m在区间[-1,1]上单调递减,在区间[1,2]上单调递增,
g(-1)=3-m,g(1)=-1-m,g(2)=-m,
所以当x2∈[-1,2]时,g(x2)∈[-1-m,3-m].
因为函数f(x)在区间[-2,1]上单调递增,
所以当x1∈[-2,1]时,f(x1)∈[-4,1],
由题意,得解得2≤m≤3,
所以实数m的取值范围为[2,3].
若 x1∈[a,b], x2∈[c,d],有f(x1)=g(x2),则f(x)的值域是g(x)值域的子集.
3. D 令u(x)=-a,则u(x)在区间[-2,0]上单调递减,所以u(x)的最小值为u(0)=1-a>0,得a<1,且u(x)∈[1-a,4-a].令g(u)=log2u,则g(u)在区间[1-a,4-a]上单调递增,所以g(u)∈[log2(1-a),log2(4-a)].因为存在x1,x2∈[-2,0],满足|f(x1)-f(x2)|≥3,则f(x)max-f(x)min≥3,所以g(u)max-g(u)min=log2(4-a)-log2(1-a)=log2≥3,解得≤a<1,所以实数a的取值范围是.
同一函数中的双变量问题一般求函数的最大值与最小值,再结合存在性问题与最值关系的转化即可求解.
4. (1) f(-2)+f(2)=+=+=-=0.
(2) f(x)==-1.
因为2x>0,所以2x+1>1,则0<<2,
所以-1<-1<1,
所以函数f(x)的值域为(-1,1).
(3) g(x)=[f(x)]2-+2a=[f(x)]2-2a=[f(x)]2-2af(x).
令t=f(x),则g(x)=h(t)=t2-2at,t∈(-1,1),函数h(t)的对称轴为直线t=a.
当a≥1时,函数h(t)在区间(-1,1)上单调递减,所以|g(x1)-g(x2)|所以(1+2a)-(1-2a)≤3,解得a≤,
此时a的取值不存在;
当a≤-1时,函数h(t)在区间(-1,1)上单调递增,所以|g(x1)-g(x2)|所以(1-2a)-(1+2a)≤3,解得a≥-,
此时a的取值不存在;
当-1所以|g(x1)-g(x2)|所以
解得1-≤a≤-1,
此时1-≤a≤-1满足要求.
综上,实数a的取值范围为[1-,-1].
本题(3)中的易错点是分类讨论时有遗漏的情况,分a≥1,a≤-1,-15. (1) 当x≤1时,g(x)=|2x-1|,
此时0<2x≤2,-1<2x-1≤1,
则0≤g(x)=|2x-1|≤1;
当x>1时,g(x)=f(x)-1=1-log2x单调递减,
此时g(x)综上所述,当x=1时,g(x)取得最大值1.
(2) 因为对任意x1∈[4,16],x2∈R,不等式f(2kx1)·f(x)>g(x2)恒成立,且g(x2)≤1,
所以对任意x1∈[4,16],f(2kx1)·f(x)>1恒成立.
由题意,得f(2kx1)·f(x)=[2-log2(2kx1)](2-log2x)=2(2-k-log2x1)(1-log2x1).
令m=log2x1,2≤m≤4,
则不等式可化为2(2-k-m)(1-m)>1,
即2m2+2(k-3)m-2k+3>0对任意m∈[2,4]恒成立.
令h(m)=2m2+2(k-3)m-2k+3,m∈[2,4],
则函数图象的开口向上,对称轴为直线m=-=.
当≤2,即k≥-1时,
h(m)min=h(2)=8+4(k-3)-2k+3>0,
解得k>,符合题意;
当2<<4,即-5h(m)min=h=>0,
即k2-2k+3<0,不等式无解,舍去;
当≥4,即k≤-5时,
h(m)min=h(4)=32+8(k-3)-2k+3=6k+11>0,
解得k>-,不符合题意,舍去.
综上,实数k的取值范围为.
一般地,已知函数y=f(x),x∈[a,b],y=g(x),x∈[c,d].
(1) 若 x1∈[a,b], x2∈[c,d],总有f(x1)(2) 若 x1∈[a,b], x2∈[c,d],有f(x1)(3) 若 x1∈[a,b], x2∈[c,d],有f(x1)
考向一 含有双变量的方程
1. (2024宁波九校期末联考)已知函数f(x)=若对任意x1∈[2,+∞),都存在唯一的x2∈(-∞,2),使得f(x2)=f(x1),则实数m的取值范围是________.
2. (2024南京师大附中期末)已知函数f(x)=x|x|,函数g(x)=x2-2x-m.
(1) 求不等式f(x3-2)>-1的解集;
(2) 若对于任意x2∈[-1,2],都存在x1∈[-2,1],使得g(x2)=f(x1),求实数m的取值范围.
考向二 含有双变量的不等式
3. (2024常州期末)已知函数f(x)=log2的定义域为[-2,0],若存在x1,x2∈[-2,0],满足|f(x1)-f(x2)|≥3,则实数a的取值范围是( )
A. B.
C. D.
4. (2023南通中学阶段考试)已知函数f(x)=.
(1) 求f(-2)+f(2)的值;
(2) 求函数f(x)的值域;
(3) 若g(x)=[f(x)]2-+2a,且对任意的x1,x2∈R,都有|g(x1)-g(x2)|<3,求实数a的取值范围.
5. (2023如皋期中)已知函数f(x)=2-log2x,g(x)=
(1) 求函数g(x)的最大值;
(2) 若对任意x1∈[4,16],x2∈R,不等式f(2kx1)·f(x)>g(x2)恒成立,求实数k的取值范围.
函数中双变量问题大致有以下几种类型:(1) 等式中的双变量问题,一般将同一变量放到同一边,利用函数的值域之间的关系建立不等式(组)求解;(2) 不等式中的双变量问题,一般将同一变量放到同一边,利用函数的最值之间的关系建立不等式(组)求解.
拉分题型8 函数中的双变量问题
1. 设函数f(x)在区间(-∞,2)和[2,+∞)上的值域分别为A,B.当m≤0时,函数y=,y=x-1在区间[2,+∞)上均单调递增,则函数f(x)=x+-1在区间[2,+∞)上单调递增;当0<≤2,即0
图1 图2
利用函数值相等求参数的取值范围,解题的关键在于对参数进行分类讨论,结合图形将题中的信息等价转化为不等式求解.
2. (1) 因为函数f(x)=x|x|的定义域为R,
且f(-x)=-x|-x|=-x|x|=-f(x),
所以函数f(x)为奇函数.
当x∈[0,+∞)时,f(x)=x2,
则f(x)在区间[0,+∞)上单调递增,
所以f(x)是R上的增函数.
又f(-1)=-1,所以不等式f(x3-2)>-1,即f(x3-2)>f(-1),
所以x3-2>-1,解得x>1,
所以不等式f(x3-2)>-1的解集为(1,+∞).
(2) 因为函数g(x)=x2-2x-m在区间[-1,1]上单调递减,在区间[1,2]上单调递增,
g(-1)=3-m,g(1)=-1-m,g(2)=-m,
所以当x2∈[-1,2]时,g(x2)∈[-1-m,3-m].
因为函数f(x)在区间[-2,1]上单调递增,
所以当x1∈[-2,1]时,f(x1)∈[-4,1],
由题意,得解得2≤m≤3,
所以实数m的取值范围为[2,3].
若 x1∈[a,b], x2∈[c,d],有f(x1)=g(x2),则f(x)的值域是g(x)值域的子集.
3. D 令u(x)=-a,则u(x)在区间[-2,0]上单调递减,所以u(x)的最小值为u(0)=1-a>0,得a<1,且u(x)∈[1-a,4-a].令g(u)=log2u,则g(u)在区间[1-a,4-a]上单调递增,所以g(u)∈[log2(1-a),log2(4-a)].因为存在x1,x2∈[-2,0],满足|f(x1)-f(x2)|≥3,则f(x)max-f(x)min≥3,所以g(u)max-g(u)min=log2(4-a)-log2(1-a)=log2≥3,解得≤a<1,所以实数a的取值范围是.
同一函数中的双变量问题一般求函数的最大值与最小值,再结合存在性问题与最值关系的转化即可求解.
4. (1) f(-2)+f(2)=+=+=-=0.
(2) f(x)==-1.
因为2x>0,所以2x+1>1,则0<<2,
所以-1<-1<1,
所以函数f(x)的值域为(-1,1).
(3) g(x)=[f(x)]2-+2a=[f(x)]2-2a=[f(x)]2-2af(x).
令t=f(x),则g(x)=h(t)=t2-2at,t∈(-1,1),函数h(t)的对称轴为直线t=a.
当a≥1时,函数h(t)在区间(-1,1)上单调递减,所以|g(x1)-g(x2)|
此时a的取值不存在;
当a≤-1时,函数h(t)在区间(-1,1)上单调递增,所以|g(x1)-g(x2)|
此时a的取值不存在;
当-1
解得1-≤a≤-1,
此时1-≤a≤-1满足要求.
综上,实数a的取值范围为[1-,-1].
本题(3)中的易错点是分类讨论时有遗漏的情况,分a≥1,a≤-1,-1
此时0<2x≤2,-1<2x-1≤1,
则0≤g(x)=|2x-1|≤1;
当x>1时,g(x)=f(x)-1=1-log2x单调递减,
此时g(x)
(2) 因为对任意x1∈[4,16],x2∈R,不等式f(2kx1)·f(x)>g(x2)恒成立,且g(x2)≤1,
所以对任意x1∈[4,16],f(2kx1)·f(x)>1恒成立.
由题意,得f(2kx1)·f(x)=[2-log2(2kx1)](2-log2x)=2(2-k-log2x1)(1-log2x1).
令m=log2x1,2≤m≤4,
则不等式可化为2(2-k-m)(1-m)>1,
即2m2+2(k-3)m-2k+3>0对任意m∈[2,4]恒成立.
令h(m)=2m2+2(k-3)m-2k+3,m∈[2,4],
则函数图象的开口向上,对称轴为直线m=-=.
当≤2,即k≥-1时,
h(m)min=h(2)=8+4(k-3)-2k+3>0,
解得k>,符合题意;
当2<<4,即-5
即k2-2k+3<0,不等式无解,舍去;
当≥4,即k≤-5时,
h(m)min=h(4)=32+8(k-3)-2k+3=6k+11>0,
解得k>-,不符合题意,舍去.
综上,实数k的取值范围为.
一般地,已知函数y=f(x),x∈[a,b],y=g(x),x∈[c,d].
(1) 若 x1∈[a,b], x2∈[c,d],总有f(x1)
同课章节目录
- 第1章 集合
- 1.1 集合的概念与表示
- 1.2 子集、全集、补集
- 1.3 交集、并集
- 第2章 常用逻辑用语
- 2.1 命题、定理、定义
- 2.2 充分条件、必要条件、冲要条件
- 2.3 全称量词命题与存在量词命题
- 第3章 不等式
- 3.1 不等式的基本性质
- 3.2 基本不等式
- 3.3 从函数观点看一元二次方程和一元二次不等式
- 第4章 指数与对数
- 4.1 指数
- 4.2 对数
- 第5章 函数概念与性质
- 5.1 函数的概念和图象
- 5.2 函数的表示方法
- 5.3 函数的单调性
- 5.4 函数的奇偶性
- 第6章 幂函数、指数函数和对数函数
- 6.1 幂函数
- 6.2 指数函数
- 6.3 对数函数
- 第7章 三角函数
- 7.1 角与弧度
- 7.2 三角函数概念
- 7.3 三角函数的图象和性质
- 7.4 三角函数应用
- 第8章 函数应用
- 8.1 二分法与求方程近似解
- 8.2 函数与数学模型
