第一单元1.4速度变化快慢的描述——加速度 (43张PPT) 高一上学期物理 人教版(2019)必修第一册
文档属性
| 名称 | 第一单元1.4速度变化快慢的描述——加速度 (43张PPT) 高一上学期物理 人教版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 11.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-08-20 19:39:33 | ||
图片预览










文档简介
(共43张PPT)
第一章 运动的描述
1.4 速度变化快慢的描述
加速度
目 录
1
2
4
加速度
加速度的方向
小结和练习
3
从 v-t 图像看加速度
问题导入
一辆小车在 10 s 内速度从 0 达到 100 km/h,一列火车在 300 s 内速度也从 0 达到 100 km/h 。虽然火车和汽车速度都从 0 达到100 km/h ,但是它们的运动状况显然不同。你觉得用“速度大”或“速度变化大”能描述这种不同吗?如果不能,应该怎样描述这种不同?
加速度
01
1
加速度
汽车有个参数叫百公里加速时间(即从静止开始加速到 100 km/h 的最短时间),赛车就比较看重从静止加速到最大速度所需要的时间。
问题 1 :如何比较 1 号车和 2 号车加速过程的不同?
问题 2 :如何比较 2 号车和 3 号车加速过程的不同?
问题 3 :如何比较 4 号车和另外三辆车加速过程的不同?
问题 4 :能不能用一个物理量将上述三个问题描述清楚?
1
加速度
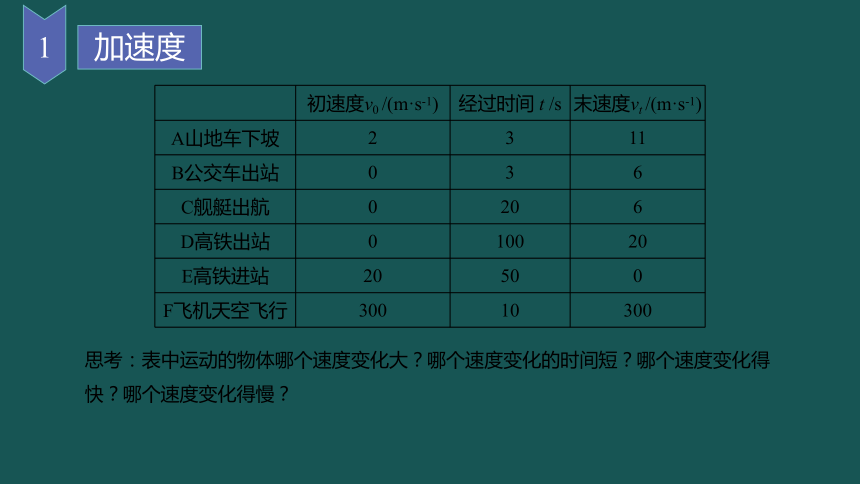
思考:表中运动的物体哪个速度变化大?哪个速度变化的时间短?哪个速度变化得快?哪个速度变化得慢?
初速度v0 /(m·s-1) 经过时间 t /s 末速度vt /(m·s-1)
A山地车下坡 2 3 11
B公交车出站 0 3 6
C舰艇出航 0 20 6
D高铁出站 0 100 20
E高铁进站 20 50 0
F飞机天空飞行 300 10 300
1
加速度
上一节的学习中,我们知道了用位移和时间之比来定义速度,即物体运动位置变化的快慢,有没有类似的概念可以用来定义物体运动速度变化的快慢呢?
物理学中把速度的变化量与发生这一变化所用的时间之比,叫作加速度。通常用 a 表示。若用 v 表示速度在时间 t 内的变化量,则有:
注意:a 的定义式是比值定义式,a 的大小与 v 和 t 无关,不能说 a 与 v 成正比,与 t 成反比。
1
加速度
比值定义法是用物理量之比定义新的物理量,是物理学中常用的方法。在初中学习中,就学过用质量和体积之比定义密度,用压力和接触面积之比定义压强,用功和时间之比定义功率等等。
运动员和飞机赛跑,刚开始时哪个快?过一段时间后哪个快?为什么?你认为运动员和飞机赛跑谁能赢?为什么?
1
加速度
1
加速度
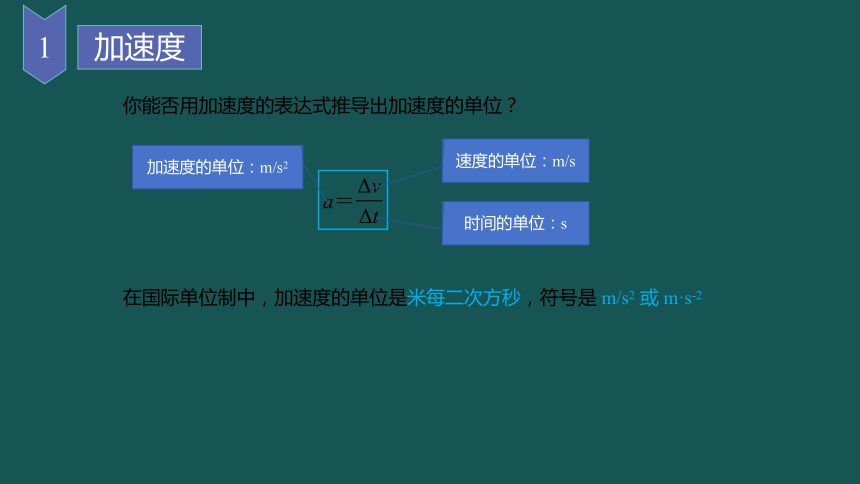
你能否用加速度的表达式推导出加速度的单位?
速度的单位:m/s
时间的单位:s
加速度的单位:m/s2
在国际单位制中,加速度的单位是米每二次方秒,符号是 m/s2 或 m·s-2
1
例 1 一辆汽车沿平直公路向东行驶,如图所示是该汽车的速度计,在汽车内的观察者观察速度计指针的变化,开始时指针指在如图甲所示的位置,经过 2 s 后指针指在如图乙所示的位置,那么汽车的加速度最接近( )
A.11 m/s2 B.-5.6 m/s2
C.1.4 m/s2 D.-1.4 m/s2
B
加速度
加速度的方向
02
思考
速度的方向和位置变化的方向相同,那么加速度的方向是不是应该和速度的变化方向相同呢?
汽车开始的速度是 v1,一段时间后变为 v2 ,v2>v1和 v2 速度是矢量,速度的变化量是矢量吗?如果是方向是怎样的?加速度是矢量吗?如果是加速度的方向应该是怎样的?
1
加速度的方向
在加速直线运动中,v2>v1,速度增大,Δv 的方向与 v 的方向相同,故 a 的方向与 v 的方向相同。
Δv
v2
v1
a
1
加速度的方向
在减速直线运动中,v2Δv
v1
v2
a
原来的速度(m/s) 后来的速度(m/s) 速度的变化量(m/s) 加速度
(m/s-2)
1 0 200 200 10
2 40 20 -20 -1
3 3 -2 -5 -500
4 199 200 1 0.05
1
加速度的方向
方向在同一条直线上的矢量,在规定正方向的前提下,可以用正负号表示矢量的方向,这样可以把矢量运算简化为代数运算。
2
加速度中的概念
观看视频,回答问题:
最终三者的速度哪个最大?
整个过程谁的速度变化最大?
起初阶段谁的速度变化最快?
2
加速度中的概念
试着举例说明下列情况:
速度大,但加速度小;
速度小,但加速度大;
速度变化量小,但加速度大;
加速度方向与速度方向相反;
加速度方向与速度变化量方向相反;
加速度增加而速度大小减小 。
2
加速度中的概念
例 2 2023年7月12日9时,朱雀二号遥二运载火箭在我国酒泉卫星发射中心成功发射,这是全球首枚成功入轨飞行的液氧甲烷火箭,火箭进入预定轨道,试验任务取得圆满成功。下列说法正确的是( )
A.火箭点火瞬间,火箭的速度和加速度都为零
B.火箭的速度越大,加速度越大
C.火箭的速度变化率越大,加速度越大
D.火箭的加速度方向与速度变化量方向可以不一致
C
2
加速度中的概念
例 3 万吨级货轮起航时,10 s 内速度大小从 0 增加到 0.2 m/s;蜻蜓以 8 m/s 的速度飞行时,能在 0.8 s 内停下来。关于两个物体的运动,下列分析不正确的是
( )
A.10 s 内货轮的速度变化量是 0.2 m/s
B.以初速度方向为正方向,货轮的加速度是 0.02 m/s2
C.货轮的速度变化比蜻蜓的慢
D.以初速度方向为正方向,蜻蜓的加速度是 10 m/s2
D
3
生活中的加速度
对运动的物体而言,可以问“它运动了多远”,这是路程或位移的概念;也可以问“它运动得多快”,这是速度的概念。然而生活用语中,却没有与加速度对应的词语。日常生活中一般只有笼统的“快”和“慢”,这里有时指的是速度,有时模模糊糊地指的是加速度。你能分别举出例子吗?
汽车起步“快”
汽车跑得“快”
3
生活中的加速度
摩托车启动“快”
猎豹的提速能力甚至超越喷气式飞机
飞机飞得“快”
3
生活中的加速度
下表为一些物体的加速度的近似值。
运动物体 a/( m·s-2 ) 运动物体 a/( m·s-2 )
子弹在枪筒中 5×104 赛车起步 4.5
跳伞者着陆 -25 汽车起步 2
汽车急刹车 -5 高铁起步 0.35
从v-t图像看加速度
03
1
从v-t 图像看加速度
v -t 图像形象地表示了物体运动变化的情况,如何从图像中直观得看出加速度呢?
0
t/s
1 2 3 4 5 6
10
8
6
4
2
(t2, v2)
(t1, v1)
v/(m·s-1)
t
v
根据加速度的定义式,我们可知 v -t 图像中图线的斜率就是速度的变化率,即加速度。
1
从v-t 图像看加速度
v -t 图像中图线向上倾斜,说明加速度方向向着正方向,向下倾斜,说明加速度方向向着反方向。图线斜率越大,说明加速度越大。
图线倾斜向上或向下倾斜,不能说明物体一定做加速运动或是减速运动。例如图线 c ,物体先做减速运动,速度减为 0 后,开始做反方向的加速运动,加速度整个过程中不变。
1
从v-t 图像看加速度
试着画一下电梯上楼和列车进出站过程中的 v-t 图像。
电梯上楼
列车进出站
1
从v-t 图像看加速度
生活中加速度和速度一样,不可能一直保持不变,下图为跳伞运动员跳伞过程中的 v-t 图像,因此加速度和速度一样也有平均加速度和瞬时加速度的概念。
1
从v-t 图像看加速度
例 4 某实验小组描绘出动车组在一段平直路段运动时其速度 v 随时间 t 变化的图像,如图所示。根据图像判断,下列说法正确的是( )
A.在 0~t1 时间内加速度逐渐增大
B.在 0~t1 时间内加速度保持不变
C.在 t1~t2 时间内加速度保持不变
D.在 t1~t2 时间内加速度逐渐增大
B
1
从v-t 图像看加速度
例 5 物体沿一条东西方向的水平线做直线运动,取向东为运动的正方向,其速度-时间图像如图所示,下列说法中正确的是( )
A.0~2 s 内,物体的加速度为 6 m/s2
B.4~6 s 内,物体的加速度为 6 m/s2
C.6~7 s 内,物体做速度方向向西的加速运动
D.10~12 s 内,物体做速度方向向东的加速运动
C
2
科学漫步
变化率
生活中很多东西都是随时间变化的,这些变化有时快、有时慢。描述变化快慢的量就是变化率。
自然界某个量的变化可以记为 ΔD,发生这个变化的时间间隔可以记为 Δt,变化量 ΔD 与 Δt 之比就是这个量对时间的变化率,简称变化率。显然,变化率在描述各种变化过程中起着非常重要的作用,速度和加速度就是两个很好的例子。
2
科学漫步
人口问题一直是国家发展的重大问题。自国家二胎政策于 2016 年 1 月 1 日全面正式放开后,据说许多家庭的生活状况发生了很大变化,这说明人口问题也是每个家庭的问题,是值的每个人关注的社会问题。以北京市 2006—2017 年常住人口的数据统计,思考并回答如下问题:
哪“一年”人口变化最多?
哪“一年”人口变化最快?
哪“两年”人口变化最快?
年份 常住人口/万人
2006 1601.0
2007 1676.0
2008 1771.0
2009 1860.0
2010 1961.9
2011 2018.6
2012 2069.3
2013 2114.8
2014 2151.6
2015 2170.5
2016 2172.9
2017 2170.7
2
科学漫步
交通工具与社会发展
人类自发明木轮车到现在制成时速 500 km/h 的磁悬浮列车,以及超音速飞机,为了获得高速的交通工具,奋斗了几千年。交通工具改变了我们的生活,我们的生活用品几乎没有一件不是交通工具运输而来的,如果没有交通工具,现代社会将会瘫痪。从世界各国的城市发展史上看,大城市规模的大小与车速的提高也密切相关。但是交通工具的发展也伴随着许多的问题,城市的规划、交通堵塞、交通意外等等。
那么,交通工具的速度是不是越快越好?
2
科学漫步
在很多国家,交通管理部门制定了死亡加速度为 5000 m/s2 这一数值以醒世人,其意思是如果行车加速度超过此值将有生命危险。一旦发生交通事故时,因为车辆碰撞时间很短,加速度将会达到这一数值。假如一辆汽车以 90 km/h 的速度行驶,因发生事故,与高速公路隔离护栏发生碰撞,碰撞时间为 0.004 s,撞后速度即变为零,那么碰撞中汽车的加速度有多大?
约为 6250 m/s2 ,所以交通工具的速度并不是越快越好。
小结和练习
04
加速度;
加速度与速度、速度的变化量、速度的变化率的关系;
加速度的方向;
从 v- t 图像分析加速度。
1
小结
加速度认知建立进程
1
小结
v
Δv
Δv/Δt
a=Δv/Δt
描述运动快慢
描述速度变化
描述速度变化快慢
物理意义:描述物体速度变化快慢;
单 位:m/s2
方 向:a与Δv 方向相同
由a与v的方向关系判定物体运动性质:
a与v 同向,物体做加速运动;
a与v 反向,物体做减速运动。
认知 进阶过程
加速度有变化快慢吗?
类比
1.有没有符合下列说法的实例?若有,请举例。
(1)物体运动的加速度等于 0 ,而速度却不等于零;
(2)两个物体相比,一个物体的速度变化量比较大,而加速度却比较小;
(3)物体具有向东的加速度,而速度的方向却向西;
(4)物体做直线运动,后一阶段的加速度比前一阶段小,但速度却比前一阶段大。
2
练习
答:(1)匀速直线运动;
(2)跑车加速到 72 km/h 只用了 4 s,高铁加速到 100 km/h 用了 80 s;
(3)物体向西做减速运动;
(4)车速加速到最大速度的过程中,汽车会做加速度减小的加速运动。
2.一质点沿 Ox 方向做加速直线运动,它离开 O 点的距离随时间 t 变化的关系为 x=6 + t3(m),它的速度随时间 t 变化的关系为 v=3t2 (m/s),该质点在 1~2 s 内的平均速度大小和 2~3 s 内的平均加速度大小分别为( )
A.6 m/s,5 m/s2 B.6 m/s,15 m/s2
C.7 m/s,5 m/s2 D.7 m/s,15 m/s2
2
练习
D
3.一个质点做方向不变的直线运动,加速度的方向始终与速度方向相反,则在质点停止运动前,关于速度和位移的变化正确的是( )
A.速度逐渐增大,位移增大
B.速度逐渐增大,位移不变
C.速度逐渐减小,位移减小
D.速度逐渐减小,位移增大
2
练习
D
4.A、B 两物体在同一直线上做变速直线运动,它们的速度—时间图像如图所示,则( )
A.A、B 两物体的运动方向一定相同
B.4 s 之前 A 比 B 运动得快
C.t=4 s 时,A、B 两物体的加速度方向相同
D.A 物体的加速度比 B 物体的加速度大
2
练习
A
5.如图所示,子弹和足球的初速度均为 v1=10 m/s,方向水平向右。设它们与木板作用的时间都是 0.1 s,那么:
(1)子弹击穿木板(木板阻力恒定)后,速度大小变为 7 m/s,方向不变,求子弹击穿木板时的加速度;
(2)足球与木板作用后反向弹回的速度大小为 7 m/s,求足球与木板碰撞反弹时的平均加速度。
2
练习
5.解析:
(1)规定向右为正方向,子弹击穿木板后,速度方向仍为正。根据加速度的定义可知 ,即子弹的加速度大小为 30 m/s2,方向水平向左。
(2)规定向右为正方向,足球与木板作用后向弹回,速度方向变为负方向,根据加速度的定义有 ,即足球的平均加速度大小为 170 m/s2 ,方向水平向左。
2
练习
第一章 运动的描述
1.4 速度变化快慢的描述
加速度
目 录
1
2
4
加速度
加速度的方向
小结和练习
3
从 v-t 图像看加速度
问题导入
一辆小车在 10 s 内速度从 0 达到 100 km/h,一列火车在 300 s 内速度也从 0 达到 100 km/h 。虽然火车和汽车速度都从 0 达到100 km/h ,但是它们的运动状况显然不同。你觉得用“速度大”或“速度变化大”能描述这种不同吗?如果不能,应该怎样描述这种不同?
加速度
01
1
加速度
汽车有个参数叫百公里加速时间(即从静止开始加速到 100 km/h 的最短时间),赛车就比较看重从静止加速到最大速度所需要的时间。
问题 1 :如何比较 1 号车和 2 号车加速过程的不同?
问题 2 :如何比较 2 号车和 3 号车加速过程的不同?
问题 3 :如何比较 4 号车和另外三辆车加速过程的不同?
问题 4 :能不能用一个物理量将上述三个问题描述清楚?
1
加速度
思考:表中运动的物体哪个速度变化大?哪个速度变化的时间短?哪个速度变化得快?哪个速度变化得慢?
初速度v0 /(m·s-1) 经过时间 t /s 末速度vt /(m·s-1)
A山地车下坡 2 3 11
B公交车出站 0 3 6
C舰艇出航 0 20 6
D高铁出站 0 100 20
E高铁进站 20 50 0
F飞机天空飞行 300 10 300
1
加速度
上一节的学习中,我们知道了用位移和时间之比来定义速度,即物体运动位置变化的快慢,有没有类似的概念可以用来定义物体运动速度变化的快慢呢?
物理学中把速度的变化量与发生这一变化所用的时间之比,叫作加速度。通常用 a 表示。若用 v 表示速度在时间 t 内的变化量,则有:
注意:a 的定义式是比值定义式,a 的大小与 v 和 t 无关,不能说 a 与 v 成正比,与 t 成反比。
1
加速度
比值定义法是用物理量之比定义新的物理量,是物理学中常用的方法。在初中学习中,就学过用质量和体积之比定义密度,用压力和接触面积之比定义压强,用功和时间之比定义功率等等。
运动员和飞机赛跑,刚开始时哪个快?过一段时间后哪个快?为什么?你认为运动员和飞机赛跑谁能赢?为什么?
1
加速度
1
加速度
你能否用加速度的表达式推导出加速度的单位?
速度的单位:m/s
时间的单位:s
加速度的单位:m/s2
在国际单位制中,加速度的单位是米每二次方秒,符号是 m/s2 或 m·s-2
1
例 1 一辆汽车沿平直公路向东行驶,如图所示是该汽车的速度计,在汽车内的观察者观察速度计指针的变化,开始时指针指在如图甲所示的位置,经过 2 s 后指针指在如图乙所示的位置,那么汽车的加速度最接近( )
A.11 m/s2 B.-5.6 m/s2
C.1.4 m/s2 D.-1.4 m/s2
B
加速度
加速度的方向
02
思考
速度的方向和位置变化的方向相同,那么加速度的方向是不是应该和速度的变化方向相同呢?
汽车开始的速度是 v1,一段时间后变为 v2 ,v2>v1和 v2
1
加速度的方向
在加速直线运动中,v2>v1,速度增大,Δv 的方向与 v 的方向相同,故 a 的方向与 v 的方向相同。
Δv
v2
v1
a
1
加速度的方向
在减速直线运动中,v2
v1
v2
a
原来的速度(m/s) 后来的速度(m/s) 速度的变化量(m/s) 加速度
(m/s-2)
1 0 200 200 10
2 40 20 -20 -1
3 3 -2 -5 -500
4 199 200 1 0.05
1
加速度的方向
方向在同一条直线上的矢量,在规定正方向的前提下,可以用正负号表示矢量的方向,这样可以把矢量运算简化为代数运算。
2
加速度中的概念
观看视频,回答问题:
最终三者的速度哪个最大?
整个过程谁的速度变化最大?
起初阶段谁的速度变化最快?
2
加速度中的概念
试着举例说明下列情况:
速度大,但加速度小;
速度小,但加速度大;
速度变化量小,但加速度大;
加速度方向与速度方向相反;
加速度方向与速度变化量方向相反;
加速度增加而速度大小减小 。
2
加速度中的概念
例 2 2023年7月12日9时,朱雀二号遥二运载火箭在我国酒泉卫星发射中心成功发射,这是全球首枚成功入轨飞行的液氧甲烷火箭,火箭进入预定轨道,试验任务取得圆满成功。下列说法正确的是( )
A.火箭点火瞬间,火箭的速度和加速度都为零
B.火箭的速度越大,加速度越大
C.火箭的速度变化率越大,加速度越大
D.火箭的加速度方向与速度变化量方向可以不一致
C
2
加速度中的概念
例 3 万吨级货轮起航时,10 s 内速度大小从 0 增加到 0.2 m/s;蜻蜓以 8 m/s 的速度飞行时,能在 0.8 s 内停下来。关于两个物体的运动,下列分析不正确的是
( )
A.10 s 内货轮的速度变化量是 0.2 m/s
B.以初速度方向为正方向,货轮的加速度是 0.02 m/s2
C.货轮的速度变化比蜻蜓的慢
D.以初速度方向为正方向,蜻蜓的加速度是 10 m/s2
D
3
生活中的加速度
对运动的物体而言,可以问“它运动了多远”,这是路程或位移的概念;也可以问“它运动得多快”,这是速度的概念。然而生活用语中,却没有与加速度对应的词语。日常生活中一般只有笼统的“快”和“慢”,这里有时指的是速度,有时模模糊糊地指的是加速度。你能分别举出例子吗?
汽车起步“快”
汽车跑得“快”
3
生活中的加速度
摩托车启动“快”
猎豹的提速能力甚至超越喷气式飞机
飞机飞得“快”
3
生活中的加速度
下表为一些物体的加速度的近似值。
运动物体 a/( m·s-2 ) 运动物体 a/( m·s-2 )
子弹在枪筒中 5×104 赛车起步 4.5
跳伞者着陆 -25 汽车起步 2
汽车急刹车 -5 高铁起步 0.35
从v-t图像看加速度
03
1
从v-t 图像看加速度
v -t 图像形象地表示了物体运动变化的情况,如何从图像中直观得看出加速度呢?
0
t/s
1 2 3 4 5 6
10
8
6
4
2
(t2, v2)
(t1, v1)
v/(m·s-1)
t
v
根据加速度的定义式,我们可知 v -t 图像中图线的斜率就是速度的变化率,即加速度。
1
从v-t 图像看加速度
v -t 图像中图线向上倾斜,说明加速度方向向着正方向,向下倾斜,说明加速度方向向着反方向。图线斜率越大,说明加速度越大。
图线倾斜向上或向下倾斜,不能说明物体一定做加速运动或是减速运动。例如图线 c ,物体先做减速运动,速度减为 0 后,开始做反方向的加速运动,加速度整个过程中不变。
1
从v-t 图像看加速度
试着画一下电梯上楼和列车进出站过程中的 v-t 图像。
电梯上楼
列车进出站
1
从v-t 图像看加速度
生活中加速度和速度一样,不可能一直保持不变,下图为跳伞运动员跳伞过程中的 v-t 图像,因此加速度和速度一样也有平均加速度和瞬时加速度的概念。
1
从v-t 图像看加速度
例 4 某实验小组描绘出动车组在一段平直路段运动时其速度 v 随时间 t 变化的图像,如图所示。根据图像判断,下列说法正确的是( )
A.在 0~t1 时间内加速度逐渐增大
B.在 0~t1 时间内加速度保持不变
C.在 t1~t2 时间内加速度保持不变
D.在 t1~t2 时间内加速度逐渐增大
B
1
从v-t 图像看加速度
例 5 物体沿一条东西方向的水平线做直线运动,取向东为运动的正方向,其速度-时间图像如图所示,下列说法中正确的是( )
A.0~2 s 内,物体的加速度为 6 m/s2
B.4~6 s 内,物体的加速度为 6 m/s2
C.6~7 s 内,物体做速度方向向西的加速运动
D.10~12 s 内,物体做速度方向向东的加速运动
C
2
科学漫步
变化率
生活中很多东西都是随时间变化的,这些变化有时快、有时慢。描述变化快慢的量就是变化率。
自然界某个量的变化可以记为 ΔD,发生这个变化的时间间隔可以记为 Δt,变化量 ΔD 与 Δt 之比就是这个量对时间的变化率,简称变化率。显然,变化率在描述各种变化过程中起着非常重要的作用,速度和加速度就是两个很好的例子。
2
科学漫步
人口问题一直是国家发展的重大问题。自国家二胎政策于 2016 年 1 月 1 日全面正式放开后,据说许多家庭的生活状况发生了很大变化,这说明人口问题也是每个家庭的问题,是值的每个人关注的社会问题。以北京市 2006—2017 年常住人口的数据统计,思考并回答如下问题:
哪“一年”人口变化最多?
哪“一年”人口变化最快?
哪“两年”人口变化最快?
年份 常住人口/万人
2006 1601.0
2007 1676.0
2008 1771.0
2009 1860.0
2010 1961.9
2011 2018.6
2012 2069.3
2013 2114.8
2014 2151.6
2015 2170.5
2016 2172.9
2017 2170.7
2
科学漫步
交通工具与社会发展
人类自发明木轮车到现在制成时速 500 km/h 的磁悬浮列车,以及超音速飞机,为了获得高速的交通工具,奋斗了几千年。交通工具改变了我们的生活,我们的生活用品几乎没有一件不是交通工具运输而来的,如果没有交通工具,现代社会将会瘫痪。从世界各国的城市发展史上看,大城市规模的大小与车速的提高也密切相关。但是交通工具的发展也伴随着许多的问题,城市的规划、交通堵塞、交通意外等等。
那么,交通工具的速度是不是越快越好?
2
科学漫步
在很多国家,交通管理部门制定了死亡加速度为 5000 m/s2 这一数值以醒世人,其意思是如果行车加速度超过此值将有生命危险。一旦发生交通事故时,因为车辆碰撞时间很短,加速度将会达到这一数值。假如一辆汽车以 90 km/h 的速度行驶,因发生事故,与高速公路隔离护栏发生碰撞,碰撞时间为 0.004 s,撞后速度即变为零,那么碰撞中汽车的加速度有多大?
约为 6250 m/s2 ,所以交通工具的速度并不是越快越好。
小结和练习
04
加速度;
加速度与速度、速度的变化量、速度的变化率的关系;
加速度的方向;
从 v- t 图像分析加速度。
1
小结
加速度认知建立进程
1
小结
v
Δv
Δv/Δt
a=Δv/Δt
描述运动快慢
描述速度变化
描述速度变化快慢
物理意义:描述物体速度变化快慢;
单 位:m/s2
方 向:a与Δv 方向相同
由a与v的方向关系判定物体运动性质:
a与v 同向,物体做加速运动;
a与v 反向,物体做减速运动。
认知 进阶过程
加速度有变化快慢吗?
类比
1.有没有符合下列说法的实例?若有,请举例。
(1)物体运动的加速度等于 0 ,而速度却不等于零;
(2)两个物体相比,一个物体的速度变化量比较大,而加速度却比较小;
(3)物体具有向东的加速度,而速度的方向却向西;
(4)物体做直线运动,后一阶段的加速度比前一阶段小,但速度却比前一阶段大。
2
练习
答:(1)匀速直线运动;
(2)跑车加速到 72 km/h 只用了 4 s,高铁加速到 100 km/h 用了 80 s;
(3)物体向西做减速运动;
(4)车速加速到最大速度的过程中,汽车会做加速度减小的加速运动。
2.一质点沿 Ox 方向做加速直线运动,它离开 O 点的距离随时间 t 变化的关系为 x=6 + t3(m),它的速度随时间 t 变化的关系为 v=3t2 (m/s),该质点在 1~2 s 内的平均速度大小和 2~3 s 内的平均加速度大小分别为( )
A.6 m/s,5 m/s2 B.6 m/s,15 m/s2
C.7 m/s,5 m/s2 D.7 m/s,15 m/s2
2
练习
D
3.一个质点做方向不变的直线运动,加速度的方向始终与速度方向相反,则在质点停止运动前,关于速度和位移的变化正确的是( )
A.速度逐渐增大,位移增大
B.速度逐渐增大,位移不变
C.速度逐渐减小,位移减小
D.速度逐渐减小,位移增大
2
练习
D
4.A、B 两物体在同一直线上做变速直线运动,它们的速度—时间图像如图所示,则( )
A.A、B 两物体的运动方向一定相同
B.4 s 之前 A 比 B 运动得快
C.t=4 s 时,A、B 两物体的加速度方向相同
D.A 物体的加速度比 B 物体的加速度大
2
练习
A
5.如图所示,子弹和足球的初速度均为 v1=10 m/s,方向水平向右。设它们与木板作用的时间都是 0.1 s,那么:
(1)子弹击穿木板(木板阻力恒定)后,速度大小变为 7 m/s,方向不变,求子弹击穿木板时的加速度;
(2)足球与木板作用后反向弹回的速度大小为 7 m/s,求足球与木板碰撞反弹时的平均加速度。
2
练习
5.解析:
(1)规定向右为正方向,子弹击穿木板后,速度方向仍为正。根据加速度的定义可知 ,即子弹的加速度大小为 30 m/s2,方向水平向左。
(2)规定向右为正方向,足球与木板作用后向弹回,速度方向变为负方向,根据加速度的定义有 ,即足球的平均加速度大小为 170 m/s2 ,方向水平向左。
2
练习
