章末综合测评2(含解析)高中物理人教版(2019)必修 第三册
文档属性
| 名称 | 章末综合测评2(含解析)高中物理人教版(2019)必修 第三册 |  | |
| 格式 | docx | ||
| 文件大小 | 511.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-08-20 19:53:41 | ||
图片预览




文档简介
章末综合测评(二)
一、选择题(共10小题,1~7题为单选题,8~10题为多选题。)
1.下列说法正确的是( )
A.电场线密集处电场强度大,电势高
B.沿电场线方向电场强度减小,电势降低
C.在电势高处电荷具有的电势能也大
D.电场强度为零处,电势不一定为零
2.据报道,我国每年有近55万人发生心源性猝死,而心脏骤停最有效的抢救方式是尽早通过AED自动除颤机给予及时治疗。某型号AED模拟治疗仪器的电容器电容是15 μF,充电至9 kV电压,如果电容器在2 ms时间内完成放电,则下列说法正确的是( )
A.电容器中间是绝缘介质,所以电路是断路,放电过程中不可能有电荷定向移动
B.电容器的击穿电压为9 kV
C.电容器充电后的电量为0.135 C
D.电容器充满电的电容是15 μF,当放电完成后,电容为0
3.把头发屑悬浮在蓖麻油里,加上电场,可以模拟出电场线的分布情况,如图甲所示是模拟孤立点电荷和金属板之间的电场照片,图乙为简化后的电场线分布情况,则( )
A.由图甲可知,电场线是真实存在的
B.图甲中,没有头发屑的地方没有电场
C.图乙中A点的电场强度小于B点的电场强度
D.图乙中电子在A点的电势能小于在B点的电势能
4.某带电粒子仅在静电力作用下由A点运动到B点,电场线、粒子在A点的初速度及运动轨迹如图所示,可以判定( )
A.粒子带负电
B.粒子的加速度减小
C.粒子的动能增加
D.粒子的电势能增加
5.(2023·浙江6月卷)某带电粒子转向器的横截面如图所示,转向器中有辐向电场。粒子从M点射入,沿着由半径分别为R1和R2的圆弧平滑连接成的虚线(等势线)运动,并从虚线上的N点射出,虚线处电场强度大小分别为E1和E2,则R1、R2和E1、E2应满足( )
A. = B. =
C. = D. =
6.利用电容传感器可检测矿井渗水,从而发出安全警报,避免事故的发生。如图所示是一种通过测量电容器电容的变化来检测液面高低的仪器原理图,电容器的两个电极分别用导线接到指示器上,指示器可显示出电容的大小。下列关于该仪器的说法正确的有 ( )
A.该仪器中电容器的电极分别是芯柱和导电液
B.芯柱外套的绝缘层越厚,该电容器的电容越大
C.如果指示器显示电容增大,则容器中液面降低
D.如果指示器显示电容减小,则容器中液面升高
7.当今医学上对某些肿瘤采用质子疗法进行治疗,该疗法用一定能量的质子束照射肿瘤杀死癌细胞。现用一直线加速器来加速质子,使其从静止开始被加速到1.0×107 m/s。已知加速电场的电场强度为1.3×105 N/C,质子的质量为1.67×10-27 kg,电荷量为1.6×10-19 C,则下列说法正确的是( )
A.加速过程中质子电势能增加
B.质子所受到的静电力约为2×10-15 N
C.质子加速需要的时间约为8×10-6 s
D.加速器加速的直线长度约为4 m
8.如图所示,用绝缘细线拴一带负电小球,在竖直平面内做圆周运动,匀强电场方向竖直向下,则( )
A.当小球运动到最高点a时,细线的张力一定最小
B.当小球运动到最低点b时,小球的速度一定最大
C.当小球运动到最高点a时,小球的电势能最小
D.小球在运动过程中机械能不守恒
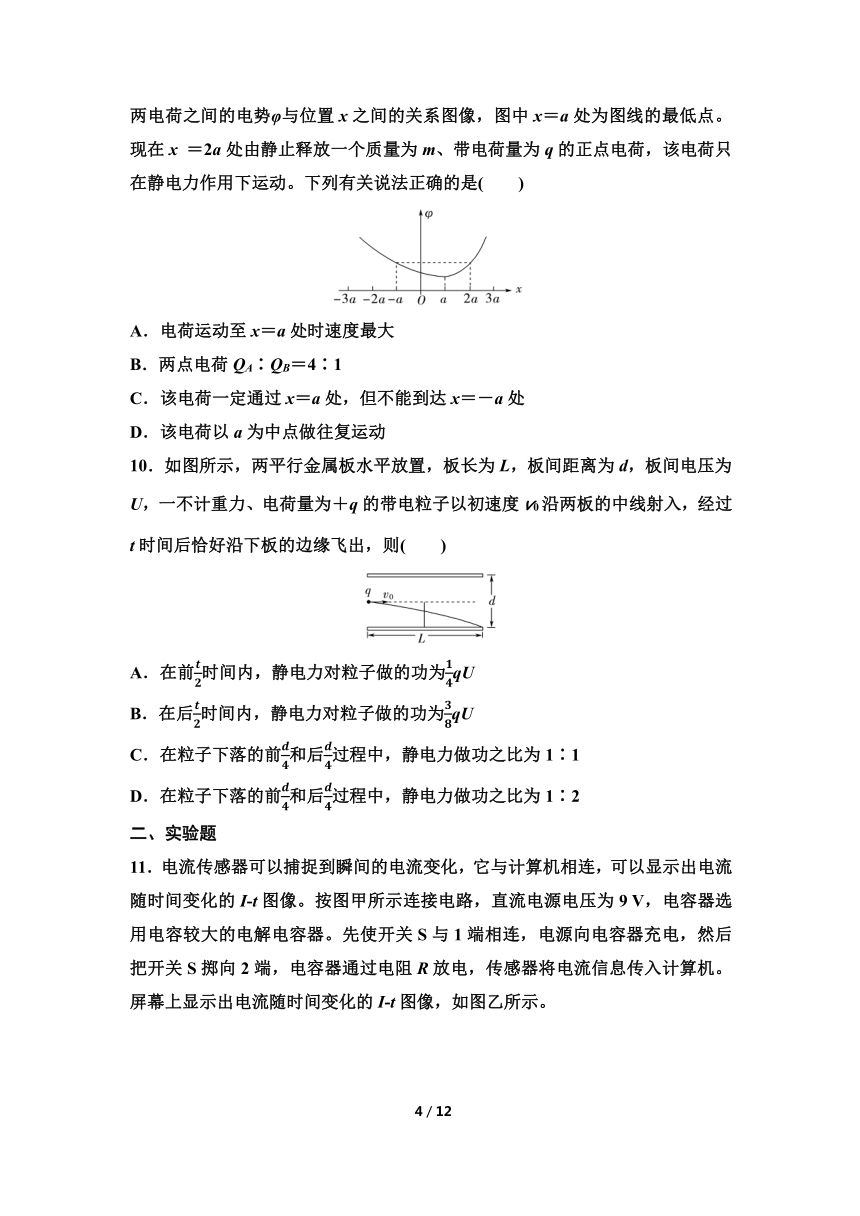
9.如图所示,在x轴的-3a和3a两处分别固定两个电荷QA、QB,图中曲线是两电荷之间的电势φ与位置x之间的关系图像,图中x=a处为图线的最低点。现在x =2a处由静止释放一个质量为m、带电荷量为q的正点电荷,该电荷只在静电力作用下运动。下列有关说法正确的是( )
A.电荷运动至x=a处时速度最大
B.两点电荷QA∶QB=4∶1
C.该电荷一定通过x=a处,但不能到达x=-a处
D.该电荷以a为中点做往复运动
10.如图所示,两平行金属板水平放置,板长为L,板间距离为d,板间电压为U,一不计重力、电荷量为+q的带电粒子以初速度v0沿两板的中线射入,经过t时间后恰好沿下板的边缘飞出,则( )
A.在前时间内,静电力对粒子做的功为qU
B.在后时间内,静电力对粒子做的功为qU
C.在粒子下落的前和后过程中,静电力做功之比为1∶1
D.在粒子下落的前和后过程中,静电力做功之比为1∶2
二、实验题
11.电流传感器可以捕捉到瞬间的电流变化,它与计算机相连,可以显示出电流随时间变化的I-t图像。按图甲所示连接电路,直流电源电压为9 V,电容器选用电容较大的电解电容器。先使开关S与1端相连,电源向电容器充电,然后把开关S掷向2端,电容器通过电阻R放电,传感器将电流信息传入计算机。屏幕上显示出电流随时间变化的I-t图像,如图乙所示。
(1)将开关S接通1,电容器的________(选填“左”或“右”)极板带正电;再将S接通2,通过R的电流方向向________(选填“左”或“右”)。
(2)根据I-t图像估算,当电容器开始放电时所带的电荷量Q=________ C,电容C=________ F。(均保留两位有效数字)
(3)如果不改变电路其他参数,只减小电阻R,充电时I-t曲线与横轴所围成的面积将________(选填“增大”“不变”或“变小”),充电时间将________(选填“变长”“不变”或“变短”)。
12.高电阻放电法测电容的实验,是通过对高阻值电阻放电的方法测出电容器充电电压为U时所带的电荷量Q,从而再求出待测电容器的电容C,某同学的实验情况如下:
(1)按图甲所示电路图连接好实验电路。
(2)接通开关S,调节电阻箱R的阻值,使小量程电流表的指针偏转接近满刻度,记下这时电流表的示数I0=500 μA、电压表的示数U0=6.0 V,I0和U0分别是电容器放电的初始电流和初始电压,此时电阻箱R的阻值为8.5 kΩ,则电流表的内阻为________kΩ。
(3)断开开关S,同时开始计时,每隔5 s或10 s读一次电流I的值,将测得数据填入预先设计的表格中,根据表格中的数据标出以时间t为横坐标、电流I为纵坐标的坐标系上的点,如图乙所示用“×”表示的点。
(4)请在图乙中描绘出电流随时间变化的图线,并根据图线估算出该电容器两端电压为U0时所带的电荷量Q0约为________C。(结果保留两位有效数字)
图甲
图乙
(5)根据公式________来计算电容器的电容。(只要求写出表达式,不要求计算结果)
三、计算题
13.如图所示,充电后的平行板电容器水平放置,电容为C,极板间距离为d,上极板正中有一小孔。质量为m,电荷量为+q的小球从小孔正上方高h处由静止开始下落,穿过小孔到达下极板处速度恰好为零(空气阻力忽略不计,极板间电场可视为匀强电场,重力加速度为g)。求:
(1)小球到达小孔处的速度;
(2)极板间电场强度大小和电容器所带电荷量;
(3)小球从开始下落到运动到下极板处所用的时间。
14.如图所示,平行板电容器A、B间的电压为U,两板间的距离为d,一质量为m、电荷量为q的粒子,由两板中央O点以水平速度v0射入,落在C处,BC=l。若将B板向下拉开,此粒子仍从O点水平射入,初速度v0不变,则粒子将落在B板上的C′点,求BC′的长度。(粒子的重力忽略不计)
15.在真空中存在着竖直向下的匀强电场,电场强度为E,如图所示。一根绝缘细线长为L,一端固定在图中的O点,另一端固定有一个质量为m、电荷量为+q、可视为点电荷的小球,O点距离地面的高度为H,将小球拉至与O点等高的位置A处从静止释放。重力加速度为g,求:
(1)小球运动到O点正下方B点时的速度大小;
(2)细线对B点处的小球的拉力大小;
(3)若小球通过B点时,细线恰好断开,小球落地点与O点的水平位移x。
章末综合测评(二)
1 2 3 4 5 6 7 8 9 10
D C D C A A D CD AB BC
1.D [电场线密集处电场强度大,电势不一定高,A错误;沿电场线方向电势降低,但电场强度不一定减小,B错误;正电荷在电势高处具有较大电势能,但对于负电荷,此现象正好相反,C错误;电场强度大小与电势高低无必然关系,D正确。]
2.C [电容器中间是绝缘介质,但两极板带等量异种电荷,放电过程电路中有电荷定向移动,故A错误;电容器可以充电至9 kV电压,电容器的击穿电压高于9 kV,故B错误;电容器充电后的电量为Q=CU=15×10-6×9×103 C=0.135 C,故C正确;电容器充满电的电容是15 μF,当放电完成后,电容不变,依然是15 μF,故D错误。]
3.D [电场是真实存在的,而电场线是为了形象描述电场而假想出来的,没画电场线的地方不代表没有电场,题图甲中头发屑是因为受到静电力的作用而按电场线的方向排列出来,A、B错误;用电场线的疏密程度表示电场强度的大小,题图乙中A点的电场强度大于B点的电场强度,C错误;若把电子从A点移动到B点,需克服静电力做功,故电势能增大,则题图乙中电子在A点的电势能小于在B点的电势能,D正确。]
4.C [粒子所受的静电力方向指向轨迹的内侧,与电场线的切线方向一致,可知粒子带正电,A错误;由电场线的疏密程度可知粒子在A点所受的静电力小于在B点所受的静电力,故粒子的加速度增加,B错误;根据题意分析可知,粒子在运动过程中静电力对其做正功,则其动能增加,电势能减小,C正确,D错误。]
5.A [带电粒子在电场中做匀速圆周运动,静电力提供向心力,则有qE1=m,qE2=m,联立可得=,故选A。]
6.A [电容器的两个电极是可以导电的,分别是金属芯柱和导电液,故A正确;芯柱外套的绝缘层越厚,金属芯柱和导电液之间距离越大,由C=可知电容减小,故B错误;如果指示器显示出电容增大了,由C=可知金属芯柱和导电液正对面积增大了,说明容器中液面升高了。如果指示器显示出电容减小了,则金属芯柱和导电液正对面积减小了,说明容器中液面降低了,故C、D错误。]
7.D [静电力对质子做正功,质子的电势能减少,A错误;质子受到的静电力大小F=qE≈2×10-14 N,B错误;质子的加速度a=≈1.2×1013 m/s2,加速时间t≈=8×10-7 s,C错误;加速器加速的直线长度x=≈4 m,D正确。]
8.CD [若qE=mg,则小球做匀速圆周运动,球在各处对细线的拉力一样大,故细线的张力一样大。若qEmg,球在a处速度最大,故A、B错误;a点电势最高,负电荷在电势最高处电势能最小,故C正确;小球在运动过程中除受到重力外,还受到静电力,静电力对小球做功,小球的机械能不守恒,故D正确。]
9.AB [由φ-x图线的斜率表示电场强度的大小可知x=a处电场强度为零,由动能定理qU=ΔEk结合点电荷从x=2a到x=a处电势差最大,所以静电力做正功最多,在x=a处速度最大,故A正确;因在x=a处电场强度为零,即=,所以QA∶QB=4∶1,故B正确;由题图知x=-a处与x=2a处电势相等且点电荷由静止释放,由动能定理可知点电荷刚好能到达x=-a处,故C错误;点电荷在x=-a与x=2a之间做往复运动,但x=a处不是运动中点,故D错误。故选AB。]
10.BC [粒子在两平行金属板间做类平抛运动,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,在前后两个的时间内沿竖直方向的位移之比为1∶3,则在前时间内,静电力对粒子做的功为qU,在后时间内,静电力对粒子做的功为qU,A错误,B正确;由W=qEx知,在粒子下落的前和后过程中,静电力做功之比为1∶1,C正确,D错误。]
11.解析:(1)将开关S接通1,电容器的左极板与电源的正极相连,所以电容器的左极板带正电;再将S接通2,电容器通过电阻R放电,所以通过R的电流方向向右。
(2)电容器所带的电荷量在数值上等于I-t图像与坐标轴所包围的面积。
每个小方格所代表的电荷量数值为
q=0.2×10-3×0.2 C=4×10-5 C
曲线下包含的小方格的个数为40(38~42都正确)。
故电容器所带的电荷量
Q=40×4×10-5 C=1.6×10-3 C
根据电容的定义式可得
C== F≈1.8×10-4 F。
(3)电容器所带的电荷量Q=CU,与电阻R无关,如果不改变电路其他参数,只减小电阻R,充电时I-t曲线与横轴所围成的面积将不变,由于电阻对电流的阻碍作用减小,充电电流增大,所以充电时间将变短。
答案:(1)左 右 (2)1.6×10-3 1.8×10-4 (3)不变 变短
12.解析:(2)由欧姆定律有U0=I0(Rg+R)
得Rg=-R=Ω-8.5×103Ω=3.5×103Ω=3.5 kΩ。
(4)用平滑曲线连接各点,数出所画的曲线与坐标轴所围的格数以求得面积。 因ΔQ=I·Δt即为曲线与坐标轴所围的格数的面积,则利用数格子方法,估算出电容器两端电压为U0时的电荷量为Q=34×2.5×10-4=8.5×10-3C。
(5)利用C=可求出电容C。
答案:(2)3.5 (4)如图所示 8.5×10-3 (5)C=
13.解析:(1)小球从开始下落到上极板间做自由落体运动,由v2=2gh,得v=。
(2)在极板间带电小球受重力和静电力作用,由牛顿第二定律得:mg-qE=ma
由运动学公式知:0-v2=2ad
整理得电场强度E=
由U=Ed,Q=CU
得电容器所带电荷量Q=。
(3)由h=,0=gt1+at2,t=t1+t2
整理得t=。
答案:(1) (2) (3)
14.解析:根据牛顿第二定律,带电粒子由O点到C点,
有q=ma,
所以a=
带电粒子在水平方向做匀速直线运动,l=v0t
在竖直方向做匀加速直线运动,
d=at2=t2
带电粒子由O点到C′点,根据牛顿第二定律得
q=ma′
所以a′=
设BC′的长度为l′,则l′=v0t′
d+d=a′t′2=·t′2
解得BC′的长度l′=l。
答案:l
15.解析:(1)小球从A到B过程,由动能定理得mgL+qEL=mv2-0
小球到达B点时的速度大小为
解得v=。
(2)在B点,对小球由牛顿第二定律得
FT-mg-qE=m
解得FT=3(mg+qE)。
(3)对小球在细线断开后的类平抛运动,由牛顿第二定律有qE+mg=ma
竖直方向:H-L=at2
水平方向:x=vt
联立解得x=2。
答案:(1) (2)3(mg+qE) (3)2
7 / 7
一、选择题(共10小题,1~7题为单选题,8~10题为多选题。)
1.下列说法正确的是( )
A.电场线密集处电场强度大,电势高
B.沿电场线方向电场强度减小,电势降低
C.在电势高处电荷具有的电势能也大
D.电场强度为零处,电势不一定为零
2.据报道,我国每年有近55万人发生心源性猝死,而心脏骤停最有效的抢救方式是尽早通过AED自动除颤机给予及时治疗。某型号AED模拟治疗仪器的电容器电容是15 μF,充电至9 kV电压,如果电容器在2 ms时间内完成放电,则下列说法正确的是( )
A.电容器中间是绝缘介质,所以电路是断路,放电过程中不可能有电荷定向移动
B.电容器的击穿电压为9 kV
C.电容器充电后的电量为0.135 C
D.电容器充满电的电容是15 μF,当放电完成后,电容为0
3.把头发屑悬浮在蓖麻油里,加上电场,可以模拟出电场线的分布情况,如图甲所示是模拟孤立点电荷和金属板之间的电场照片,图乙为简化后的电场线分布情况,则( )
A.由图甲可知,电场线是真实存在的
B.图甲中,没有头发屑的地方没有电场
C.图乙中A点的电场强度小于B点的电场强度
D.图乙中电子在A点的电势能小于在B点的电势能
4.某带电粒子仅在静电力作用下由A点运动到B点,电场线、粒子在A点的初速度及运动轨迹如图所示,可以判定( )
A.粒子带负电
B.粒子的加速度减小
C.粒子的动能增加
D.粒子的电势能增加
5.(2023·浙江6月卷)某带电粒子转向器的横截面如图所示,转向器中有辐向电场。粒子从M点射入,沿着由半径分别为R1和R2的圆弧平滑连接成的虚线(等势线)运动,并从虚线上的N点射出,虚线处电场强度大小分别为E1和E2,则R1、R2和E1、E2应满足( )
A. = B. =
C. = D. =
6.利用电容传感器可检测矿井渗水,从而发出安全警报,避免事故的发生。如图所示是一种通过测量电容器电容的变化来检测液面高低的仪器原理图,电容器的两个电极分别用导线接到指示器上,指示器可显示出电容的大小。下列关于该仪器的说法正确的有 ( )
A.该仪器中电容器的电极分别是芯柱和导电液
B.芯柱外套的绝缘层越厚,该电容器的电容越大
C.如果指示器显示电容增大,则容器中液面降低
D.如果指示器显示电容减小,则容器中液面升高
7.当今医学上对某些肿瘤采用质子疗法进行治疗,该疗法用一定能量的质子束照射肿瘤杀死癌细胞。现用一直线加速器来加速质子,使其从静止开始被加速到1.0×107 m/s。已知加速电场的电场强度为1.3×105 N/C,质子的质量为1.67×10-27 kg,电荷量为1.6×10-19 C,则下列说法正确的是( )
A.加速过程中质子电势能增加
B.质子所受到的静电力约为2×10-15 N
C.质子加速需要的时间约为8×10-6 s
D.加速器加速的直线长度约为4 m
8.如图所示,用绝缘细线拴一带负电小球,在竖直平面内做圆周运动,匀强电场方向竖直向下,则( )
A.当小球运动到最高点a时,细线的张力一定最小
B.当小球运动到最低点b时,小球的速度一定最大
C.当小球运动到最高点a时,小球的电势能最小
D.小球在运动过程中机械能不守恒
9.如图所示,在x轴的-3a和3a两处分别固定两个电荷QA、QB,图中曲线是两电荷之间的电势φ与位置x之间的关系图像,图中x=a处为图线的最低点。现在x =2a处由静止释放一个质量为m、带电荷量为q的正点电荷,该电荷只在静电力作用下运动。下列有关说法正确的是( )
A.电荷运动至x=a处时速度最大
B.两点电荷QA∶QB=4∶1
C.该电荷一定通过x=a处,但不能到达x=-a处
D.该电荷以a为中点做往复运动
10.如图所示,两平行金属板水平放置,板长为L,板间距离为d,板间电压为U,一不计重力、电荷量为+q的带电粒子以初速度v0沿两板的中线射入,经过t时间后恰好沿下板的边缘飞出,则( )
A.在前时间内,静电力对粒子做的功为qU
B.在后时间内,静电力对粒子做的功为qU
C.在粒子下落的前和后过程中,静电力做功之比为1∶1
D.在粒子下落的前和后过程中,静电力做功之比为1∶2
二、实验题
11.电流传感器可以捕捉到瞬间的电流变化,它与计算机相连,可以显示出电流随时间变化的I-t图像。按图甲所示连接电路,直流电源电压为9 V,电容器选用电容较大的电解电容器。先使开关S与1端相连,电源向电容器充电,然后把开关S掷向2端,电容器通过电阻R放电,传感器将电流信息传入计算机。屏幕上显示出电流随时间变化的I-t图像,如图乙所示。
(1)将开关S接通1,电容器的________(选填“左”或“右”)极板带正电;再将S接通2,通过R的电流方向向________(选填“左”或“右”)。
(2)根据I-t图像估算,当电容器开始放电时所带的电荷量Q=________ C,电容C=________ F。(均保留两位有效数字)
(3)如果不改变电路其他参数,只减小电阻R,充电时I-t曲线与横轴所围成的面积将________(选填“增大”“不变”或“变小”),充电时间将________(选填“变长”“不变”或“变短”)。
12.高电阻放电法测电容的实验,是通过对高阻值电阻放电的方法测出电容器充电电压为U时所带的电荷量Q,从而再求出待测电容器的电容C,某同学的实验情况如下:
(1)按图甲所示电路图连接好实验电路。
(2)接通开关S,调节电阻箱R的阻值,使小量程电流表的指针偏转接近满刻度,记下这时电流表的示数I0=500 μA、电压表的示数U0=6.0 V,I0和U0分别是电容器放电的初始电流和初始电压,此时电阻箱R的阻值为8.5 kΩ,则电流表的内阻为________kΩ。
(3)断开开关S,同时开始计时,每隔5 s或10 s读一次电流I的值,将测得数据填入预先设计的表格中,根据表格中的数据标出以时间t为横坐标、电流I为纵坐标的坐标系上的点,如图乙所示用“×”表示的点。
(4)请在图乙中描绘出电流随时间变化的图线,并根据图线估算出该电容器两端电压为U0时所带的电荷量Q0约为________C。(结果保留两位有效数字)
图甲
图乙
(5)根据公式________来计算电容器的电容。(只要求写出表达式,不要求计算结果)
三、计算题
13.如图所示,充电后的平行板电容器水平放置,电容为C,极板间距离为d,上极板正中有一小孔。质量为m,电荷量为+q的小球从小孔正上方高h处由静止开始下落,穿过小孔到达下极板处速度恰好为零(空气阻力忽略不计,极板间电场可视为匀强电场,重力加速度为g)。求:
(1)小球到达小孔处的速度;
(2)极板间电场强度大小和电容器所带电荷量;
(3)小球从开始下落到运动到下极板处所用的时间。
14.如图所示,平行板电容器A、B间的电压为U,两板间的距离为d,一质量为m、电荷量为q的粒子,由两板中央O点以水平速度v0射入,落在C处,BC=l。若将B板向下拉开,此粒子仍从O点水平射入,初速度v0不变,则粒子将落在B板上的C′点,求BC′的长度。(粒子的重力忽略不计)
15.在真空中存在着竖直向下的匀强电场,电场强度为E,如图所示。一根绝缘细线长为L,一端固定在图中的O点,另一端固定有一个质量为m、电荷量为+q、可视为点电荷的小球,O点距离地面的高度为H,将小球拉至与O点等高的位置A处从静止释放。重力加速度为g,求:
(1)小球运动到O点正下方B点时的速度大小;
(2)细线对B点处的小球的拉力大小;
(3)若小球通过B点时,细线恰好断开,小球落地点与O点的水平位移x。
章末综合测评(二)
1 2 3 4 5 6 7 8 9 10
D C D C A A D CD AB BC
1.D [电场线密集处电场强度大,电势不一定高,A错误;沿电场线方向电势降低,但电场强度不一定减小,B错误;正电荷在电势高处具有较大电势能,但对于负电荷,此现象正好相反,C错误;电场强度大小与电势高低无必然关系,D正确。]
2.C [电容器中间是绝缘介质,但两极板带等量异种电荷,放电过程电路中有电荷定向移动,故A错误;电容器可以充电至9 kV电压,电容器的击穿电压高于9 kV,故B错误;电容器充电后的电量为Q=CU=15×10-6×9×103 C=0.135 C,故C正确;电容器充满电的电容是15 μF,当放电完成后,电容不变,依然是15 μF,故D错误。]
3.D [电场是真实存在的,而电场线是为了形象描述电场而假想出来的,没画电场线的地方不代表没有电场,题图甲中头发屑是因为受到静电力的作用而按电场线的方向排列出来,A、B错误;用电场线的疏密程度表示电场强度的大小,题图乙中A点的电场强度大于B点的电场强度,C错误;若把电子从A点移动到B点,需克服静电力做功,故电势能增大,则题图乙中电子在A点的电势能小于在B点的电势能,D正确。]
4.C [粒子所受的静电力方向指向轨迹的内侧,与电场线的切线方向一致,可知粒子带正电,A错误;由电场线的疏密程度可知粒子在A点所受的静电力小于在B点所受的静电力,故粒子的加速度增加,B错误;根据题意分析可知,粒子在运动过程中静电力对其做正功,则其动能增加,电势能减小,C正确,D错误。]
5.A [带电粒子在电场中做匀速圆周运动,静电力提供向心力,则有qE1=m,qE2=m,联立可得=,故选A。]
6.A [电容器的两个电极是可以导电的,分别是金属芯柱和导电液,故A正确;芯柱外套的绝缘层越厚,金属芯柱和导电液之间距离越大,由C=可知电容减小,故B错误;如果指示器显示出电容增大了,由C=可知金属芯柱和导电液正对面积增大了,说明容器中液面升高了。如果指示器显示出电容减小了,则金属芯柱和导电液正对面积减小了,说明容器中液面降低了,故C、D错误。]
7.D [静电力对质子做正功,质子的电势能减少,A错误;质子受到的静电力大小F=qE≈2×10-14 N,B错误;质子的加速度a=≈1.2×1013 m/s2,加速时间t≈=8×10-7 s,C错误;加速器加速的直线长度x=≈4 m,D正确。]
8.CD [若qE=mg,则小球做匀速圆周运动,球在各处对细线的拉力一样大,故细线的张力一样大。若qE
9.AB [由φ-x图线的斜率表示电场强度的大小可知x=a处电场强度为零,由动能定理qU=ΔEk结合点电荷从x=2a到x=a处电势差最大,所以静电力做正功最多,在x=a处速度最大,故A正确;因在x=a处电场强度为零,即=,所以QA∶QB=4∶1,故B正确;由题图知x=-a处与x=2a处电势相等且点电荷由静止释放,由动能定理可知点电荷刚好能到达x=-a处,故C错误;点电荷在x=-a与x=2a之间做往复运动,但x=a处不是运动中点,故D错误。故选AB。]
10.BC [粒子在两平行金属板间做类平抛运动,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,在前后两个的时间内沿竖直方向的位移之比为1∶3,则在前时间内,静电力对粒子做的功为qU,在后时间内,静电力对粒子做的功为qU,A错误,B正确;由W=qEx知,在粒子下落的前和后过程中,静电力做功之比为1∶1,C正确,D错误。]
11.解析:(1)将开关S接通1,电容器的左极板与电源的正极相连,所以电容器的左极板带正电;再将S接通2,电容器通过电阻R放电,所以通过R的电流方向向右。
(2)电容器所带的电荷量在数值上等于I-t图像与坐标轴所包围的面积。
每个小方格所代表的电荷量数值为
q=0.2×10-3×0.2 C=4×10-5 C
曲线下包含的小方格的个数为40(38~42都正确)。
故电容器所带的电荷量
Q=40×4×10-5 C=1.6×10-3 C
根据电容的定义式可得
C== F≈1.8×10-4 F。
(3)电容器所带的电荷量Q=CU,与电阻R无关,如果不改变电路其他参数,只减小电阻R,充电时I-t曲线与横轴所围成的面积将不变,由于电阻对电流的阻碍作用减小,充电电流增大,所以充电时间将变短。
答案:(1)左 右 (2)1.6×10-3 1.8×10-4 (3)不变 变短
12.解析:(2)由欧姆定律有U0=I0(Rg+R)
得Rg=-R=Ω-8.5×103Ω=3.5×103Ω=3.5 kΩ。
(4)用平滑曲线连接各点,数出所画的曲线与坐标轴所围的格数以求得面积。 因ΔQ=I·Δt即为曲线与坐标轴所围的格数的面积,则利用数格子方法,估算出电容器两端电压为U0时的电荷量为Q=34×2.5×10-4=8.5×10-3C。
(5)利用C=可求出电容C。
答案:(2)3.5 (4)如图所示 8.5×10-3 (5)C=
13.解析:(1)小球从开始下落到上极板间做自由落体运动,由v2=2gh,得v=。
(2)在极板间带电小球受重力和静电力作用,由牛顿第二定律得:mg-qE=ma
由运动学公式知:0-v2=2ad
整理得电场强度E=
由U=Ed,Q=CU
得电容器所带电荷量Q=。
(3)由h=,0=gt1+at2,t=t1+t2
整理得t=。
答案:(1) (2) (3)
14.解析:根据牛顿第二定律,带电粒子由O点到C点,
有q=ma,
所以a=
带电粒子在水平方向做匀速直线运动,l=v0t
在竖直方向做匀加速直线运动,
d=at2=t2
带电粒子由O点到C′点,根据牛顿第二定律得
q=ma′
所以a′=
设BC′的长度为l′,则l′=v0t′
d+d=a′t′2=·t′2
解得BC′的长度l′=l。
答案:l
15.解析:(1)小球从A到B过程,由动能定理得mgL+qEL=mv2-0
小球到达B点时的速度大小为
解得v=。
(2)在B点,对小球由牛顿第二定律得
FT-mg-qE=m
解得FT=3(mg+qE)。
(3)对小球在细线断开后的类平抛运动,由牛顿第二定律有qE+mg=ma
竖直方向:H-L=at2
水平方向:x=vt
联立解得x=2。
答案:(1) (2)3(mg+qE) (3)2
7 / 7
同课章节目录
- 第九章 静电场及其应用
- 1 电荷
- 2 库仑定律
- 3 电场 电场强度
- 4 静电的防止与利用
- 第十章 静电场中的能量
- 1 电势能和电势
- 2 电势差
- 3 电势差与电场强度的关系
- 4 电容器的电容
- 5 带电粒子在电场中的运动
- 第十一章 电路及其应用
- 1 电源和电流
- 2 导体的电阻
- 3 实验:导体电阻率的测量
- 4 串联电路和并联电路
- 5 实验:练习使用多用电表
- 第十二章 电能 能量守恒定律
- 1 电路中的能量转化
- 2 闭合电路的欧姆定律
- 3 实验:电池电动势和内阻的测量
- 4 能源与可持续发展
- 第十三章 电磁感应与电磁波初步
- 1 磁场 磁感线
- 2 磁感应强度 磁通量
- 3 电磁感应现象及应用
- 4 电磁波的发现及应用
- 5 能量量子化
