3.4 函数的应用(一) 同步课件 (18张PPT) 高一数学人教A版2019必修一
文档属性
| 名称 | 3.4 函数的应用(一) 同步课件 (18张PPT) 高一数学人教A版2019必修一 |

|
|
| 格式 | pptx | ||
| 文件大小 | 29.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
第三章
函数的概念与性质
3.4 函数的应用(一)
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
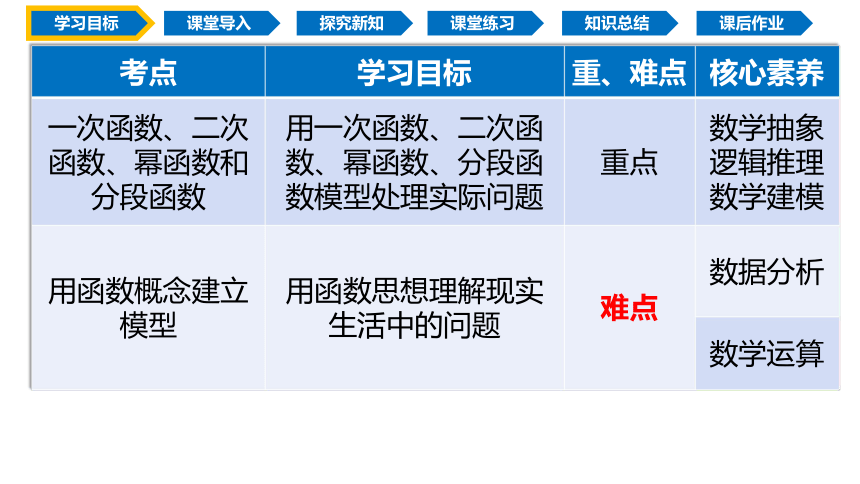
考点 学习目标 重、难点 核心素养
一次函数、二次函数、幂函数和分段函数 用一次函数、二次函数、幂函数、分段函数模型处理实际问题 重点 数学抽象
逻辑推理
数学建模
用函数概念建立模型 用函数思想理解现实生活中的问题 难点 数据分析
数学运算
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
1
问题1:面对实际问题,我们需要选择合适的函数类型刻画其中的变化规律.
我们学过哪些类型的函数
常 见 的 函 数 模 型 一次函数
二次函数
幂函数型
分段函数
例1. 设小王的专项扣除比例、专项附加扣除金额、依法确定的其他扣除金额与3.1.2例8相同,全年综合所得收入额为x(单位:元),应缴纳综合所得个税税额为y(单位:元).
(1)求y关于x的函数解析式;
(2)如果小王全年的综合所得由189600元增加到249600元,那么他全年应缴纳多少综合所得个税?
课前思考
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
2
分析:由3.1.2例8公式②,可得应纳税所得额t关于综合所得收入额x的解析式t=g(x),再结合y=f(x)的解析式③,即可得出y关于x的函数解析式。
解:(1)由个人应纳税所得额计算公式,可得
令
课前思考
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
3
根据个人应纳税所得额的规定可知,当时,所以,个人应纳税所得额关于综合所得收入的函数解析式为
结合3.1.2例8的解析式③,可得:
课前思考
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
4
④
课前思考
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
5
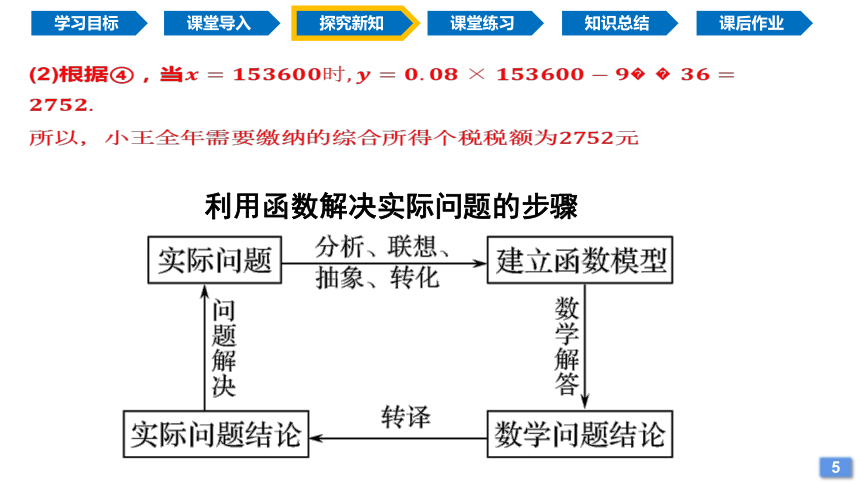
(2)根据④,当
所以,小王全年需要缴纳的综合所得个税税额为2752元
利用函数解决实际问题的步骤
例2. 一辆汽车在某段路程中行驶的平均速率v(单位:km/h)与时间t(单位:h)的关系如图3.4-1所示,
(1)求图3.4-1中阴影部分的面积,并说明所求面积的实际含义;
课前思考
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
6
分析:当时间t在[0, 5]内变化时,对于任意的时刻t都有唯一确定的行驶路程与之相对应.根据图3.4-1,在时间段[0, 1),[1, 2),[2, 3),[3, 4),[4, 5]内行驶的平均速率分别为50 km/h,80 km/h,90 km/h,75 km/h,65 km/h,因此在每个时间段内,行驶路程与时间的关系也不一样,需要分段表述
阴影部分的面积表示汽车在这5 h内行驶的路程为360 km.
能根据图3.4-1画出汽车行驶路程关于时间变化的图象吗?
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2 004 km,试建立行驶这段路程时汽车里程表读数s(单位:km)与时间t 的函数解析式,并画出相应的图象.
课前思考
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
7
本题的解答过程表明,函数图象对分析和理解题意很有帮助.因此,我们要提高读图能力.另外,本题用到了分段函数,解决现实问题时经常会用到这类函数.
题型一 幂函数的概念
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
8
解:(1)设y与x之间的函数解析式为y=kx+b.
由图象可知,当x=60时,y=6;当x=80时,y=10.
所以,解得k=,b=-6.
所以y与x之间的函数解析式为y=x-6(x≥30).
(2)根据题意,当y=0时,x=30.
所以旅客最多可免费携带行李的质量为30 kg.
1.某长途汽车客运公司规定旅客可随身携带一定质量的行李,若超过规定的质量,则需购买行李票.行李费用y(单位:元)是行李质量x(单位:kg)的一次函数,其图象如图所示.
(1)根据图象数据,求y与x之间的函数解析式;
(2)旅客最多可免费携带行李的质量是多少
题型二 二次函数模型
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
9
某租车公司拥有汽车100辆,当每辆车的月租金为3 000元时,可全部租出,当每辆车的月租金每增加60元时,未租出的车将会增加一辆.租出的车每月需要维护费160元,未租出的车每月需要维护费40元.
①当每辆车的月租金定为3 900元时,能租出多少辆车
②当每辆车的月租金为多少元时,租车公司的月收益最大 最大月收益是多少
解:①租金增加了900元,900÷60=15,所以未租出的车有15辆,一共能租出85辆.
②设租金提高后有x辆未租出,则已租出(100-x)辆.租赁公司的月收益为y元,y=(3 000+60x)(100-x)-160(100-x)-40x,其中x∈[0,100],x∈N,整理得y=-60x2+3 120x+284 000=-60(x-26)2+324 560,当x=26时,y=324 560,即最大月收益为324 560元.此时,月租金为3 000+60×26=4 560(元).
题型三 幂函数模型
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
10
(1)某药厂研制出一种新型药剂,投放市场后其广告投入x(单位:万元)与药品利润y(单位:万元)存在的关系为y=xα(α为常数),其中x不超过5万元.已知去年投入广告费用为3万元时,药品利润为27万元.若今年广告费用投入5万元,预计今年药品利润为 万元.
解析:由已知投入广告费用为3万元时,药品利润为27万元,代入y=xα中,即3α=27,解得α=3,故函数解析式为y=x3.所以当x=5时,y=125.
125
题型三 幂函数模型
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
11
(2)在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量速率R(单位:cm3/s)与管道半径r(单位:cm)的四次方成正比.比例系数为k(k>0).
①试写出气体流量速率R关于管道半径r的函数解析式;
②若气体在半径为3 cm的管道中,流量速率为400 cm3/s,求气体通过半径为r的管道时,其流量速率R的解析式.
题型四 分段函数模型
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
12
国庆期间,某旅行社组团去某风景区旅游,若旅行团人数在30人或30人以下,则飞机票价格为900元;若旅行团人数多于30人,则给予优惠:每多1人,飞机票价格就减少10元,直到达到规定人数75人为止.旅行团乘飞机,旅行社需付给航空公司包机费15 000元.
(1)写出飞机票的价格关于人数的函数.
题型四 分段函数模型
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
13
(2)旅行团人数为多少时,旅行社可获得最大利润
课堂小结
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
14
课后作业
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
15
1.完成本节练习第1、2、3题
2.完成习题3.4 第1、2、3题
感谢观看
第三章
函数的概念与性质
3.4 函数的应用(一)
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
考点 学习目标 重、难点 核心素养
一次函数、二次函数、幂函数和分段函数 用一次函数、二次函数、幂函数、分段函数模型处理实际问题 重点 数学抽象
逻辑推理
数学建模
用函数概念建立模型 用函数思想理解现实生活中的问题 难点 数据分析
数学运算
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
1
问题1:面对实际问题,我们需要选择合适的函数类型刻画其中的变化规律.
我们学过哪些类型的函数
常 见 的 函 数 模 型 一次函数
二次函数
幂函数型
分段函数
例1. 设小王的专项扣除比例、专项附加扣除金额、依法确定的其他扣除金额与3.1.2例8相同,全年综合所得收入额为x(单位:元),应缴纳综合所得个税税额为y(单位:元).
(1)求y关于x的函数解析式;
(2)如果小王全年的综合所得由189600元增加到249600元,那么他全年应缴纳多少综合所得个税?
课前思考
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
2
分析:由3.1.2例8公式②,可得应纳税所得额t关于综合所得收入额x的解析式t=g(x),再结合y=f(x)的解析式③,即可得出y关于x的函数解析式。
解:(1)由个人应纳税所得额计算公式,可得
令
课前思考
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
3
根据个人应纳税所得额的规定可知,当时,所以,个人应纳税所得额关于综合所得收入的函数解析式为
结合3.1.2例8的解析式③,可得:
课前思考
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
4
④
课前思考
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
5
(2)根据④,当
所以,小王全年需要缴纳的综合所得个税税额为2752元
利用函数解决实际问题的步骤
例2. 一辆汽车在某段路程中行驶的平均速率v(单位:km/h)与时间t(单位:h)的关系如图3.4-1所示,
(1)求图3.4-1中阴影部分的面积,并说明所求面积的实际含义;
课前思考
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
6
分析:当时间t在[0, 5]内变化时,对于任意的时刻t都有唯一确定的行驶路程与之相对应.根据图3.4-1,在时间段[0, 1),[1, 2),[2, 3),[3, 4),[4, 5]内行驶的平均速率分别为50 km/h,80 km/h,90 km/h,75 km/h,65 km/h,因此在每个时间段内,行驶路程与时间的关系也不一样,需要分段表述
阴影部分的面积表示汽车在这5 h内行驶的路程为360 km.
能根据图3.4-1画出汽车行驶路程关于时间变化的图象吗?
(2)假设这辆汽车的里程表在汽车行驶这段路程前的读数为2 004 km,试建立行驶这段路程时汽车里程表读数s(单位:km)与时间t 的函数解析式,并画出相应的图象.
课前思考
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
7
本题的解答过程表明,函数图象对分析和理解题意很有帮助.因此,我们要提高读图能力.另外,本题用到了分段函数,解决现实问题时经常会用到这类函数.
题型一 幂函数的概念
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
8
解:(1)设y与x之间的函数解析式为y=kx+b.
由图象可知,当x=60时,y=6;当x=80时,y=10.
所以,解得k=,b=-6.
所以y与x之间的函数解析式为y=x-6(x≥30).
(2)根据题意,当y=0时,x=30.
所以旅客最多可免费携带行李的质量为30 kg.
1.某长途汽车客运公司规定旅客可随身携带一定质量的行李,若超过规定的质量,则需购买行李票.行李费用y(单位:元)是行李质量x(单位:kg)的一次函数,其图象如图所示.
(1)根据图象数据,求y与x之间的函数解析式;
(2)旅客最多可免费携带行李的质量是多少
题型二 二次函数模型
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
9
某租车公司拥有汽车100辆,当每辆车的月租金为3 000元时,可全部租出,当每辆车的月租金每增加60元时,未租出的车将会增加一辆.租出的车每月需要维护费160元,未租出的车每月需要维护费40元.
①当每辆车的月租金定为3 900元时,能租出多少辆车
②当每辆车的月租金为多少元时,租车公司的月收益最大 最大月收益是多少
解:①租金增加了900元,900÷60=15,所以未租出的车有15辆,一共能租出85辆.
②设租金提高后有x辆未租出,则已租出(100-x)辆.租赁公司的月收益为y元,y=(3 000+60x)(100-x)-160(100-x)-40x,其中x∈[0,100],x∈N,整理得y=-60x2+3 120x+284 000=-60(x-26)2+324 560,当x=26时,y=324 560,即最大月收益为324 560元.此时,月租金为3 000+60×26=4 560(元).
题型三 幂函数模型
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
10
(1)某药厂研制出一种新型药剂,投放市场后其广告投入x(单位:万元)与药品利润y(单位:万元)存在的关系为y=xα(α为常数),其中x不超过5万元.已知去年投入广告费用为3万元时,药品利润为27万元.若今年广告费用投入5万元,预计今年药品利润为 万元.
解析:由已知投入广告费用为3万元时,药品利润为27万元,代入y=xα中,即3α=27,解得α=3,故函数解析式为y=x3.所以当x=5时,y=125.
125
题型三 幂函数模型
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
11
(2)在固定压力差(压力差为常数)下,当气体通过圆形管道时,其流量速率R(单位:cm3/s)与管道半径r(单位:cm)的四次方成正比.比例系数为k(k>0).
①试写出气体流量速率R关于管道半径r的函数解析式;
②若气体在半径为3 cm的管道中,流量速率为400 cm3/s,求气体通过半径为r的管道时,其流量速率R的解析式.
题型四 分段函数模型
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
12
国庆期间,某旅行社组团去某风景区旅游,若旅行团人数在30人或30人以下,则飞机票价格为900元;若旅行团人数多于30人,则给予优惠:每多1人,飞机票价格就减少10元,直到达到规定人数75人为止.旅行团乘飞机,旅行社需付给航空公司包机费15 000元.
(1)写出飞机票的价格关于人数的函数.
题型四 分段函数模型
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
13
(2)旅行团人数为多少时,旅行社可获得最大利润
课堂小结
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
14
课后作业
学习目标
课堂导入
探究新知
课堂练习
知识总结
课后作业
15
1.完成本节练习第1、2、3题
2.完成习题3.4 第1、2、3题
感谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
