第一单元第01课时根据从同一个方向观察形状图 摆立方体 例1(分层作业)(含答案)五年级数学下册人教版
文档属性
| 名称 | 第一单元第01课时根据从同一个方向观察形状图 摆立方体 例1(分层作业)(含答案)五年级数学下册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 639.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 11:07:21 | ||
图片预览

文档简介
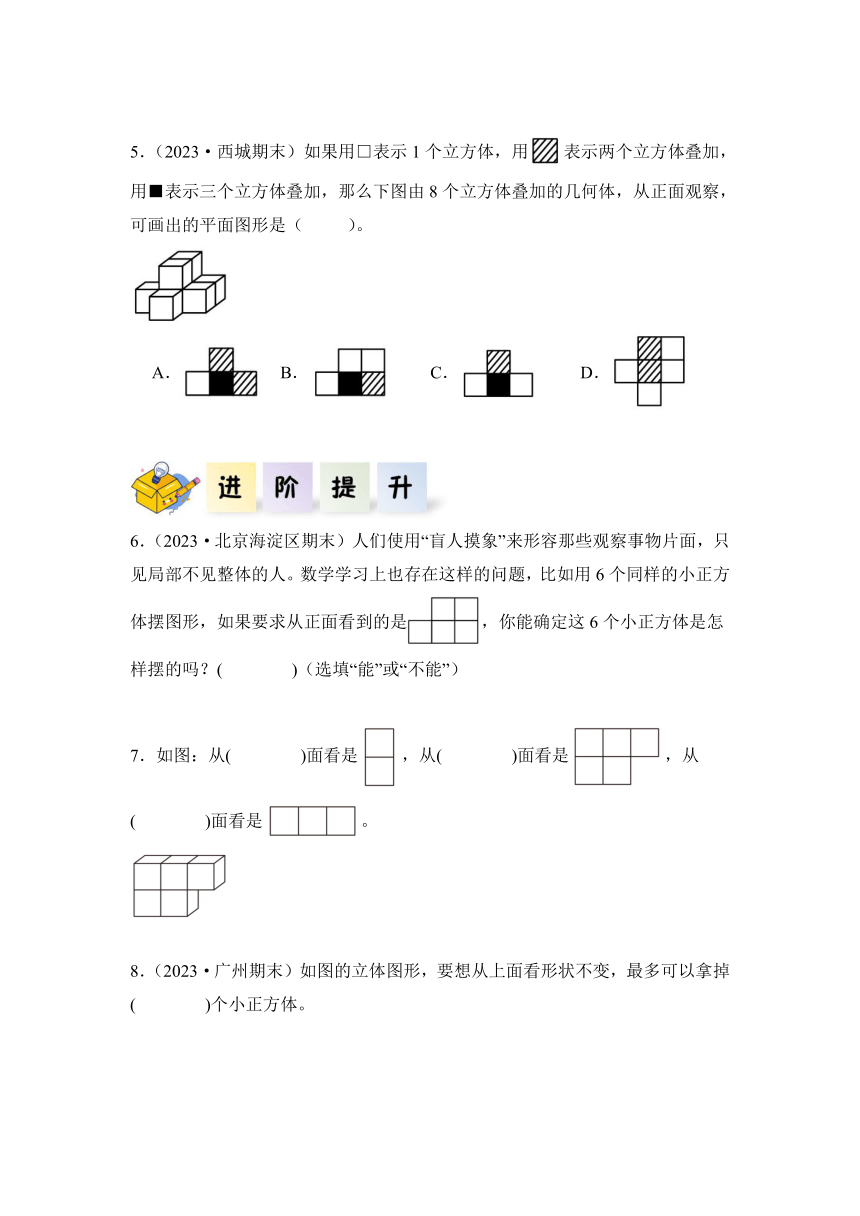
第1课时 从同一个方向观察形状图摆小正方体 分层作业
1.是从的( )面看到的形状。
A.上 B.正 C.左
2.(2023·南京期末)用同样的小正方体搭一个几何体,从上面看到的图形如下图(每个正方形上面的数字表示在这个位置上所用的小正方体的个数)。这个几何体从前面看是( )。
A. B. C. D.
3.从左面看到的图形是的是( )。
A. B. C. D.
4.(2023·常州期末)从前面、上面、左面和右面观察下面的几何体,关于看到的形状描述正确的是( )。
A.四个面看到的形状相同 B.左面和右面看到的形状相同
C.前面和左面看到的形状相同 D.前面和右面看到的形状相同
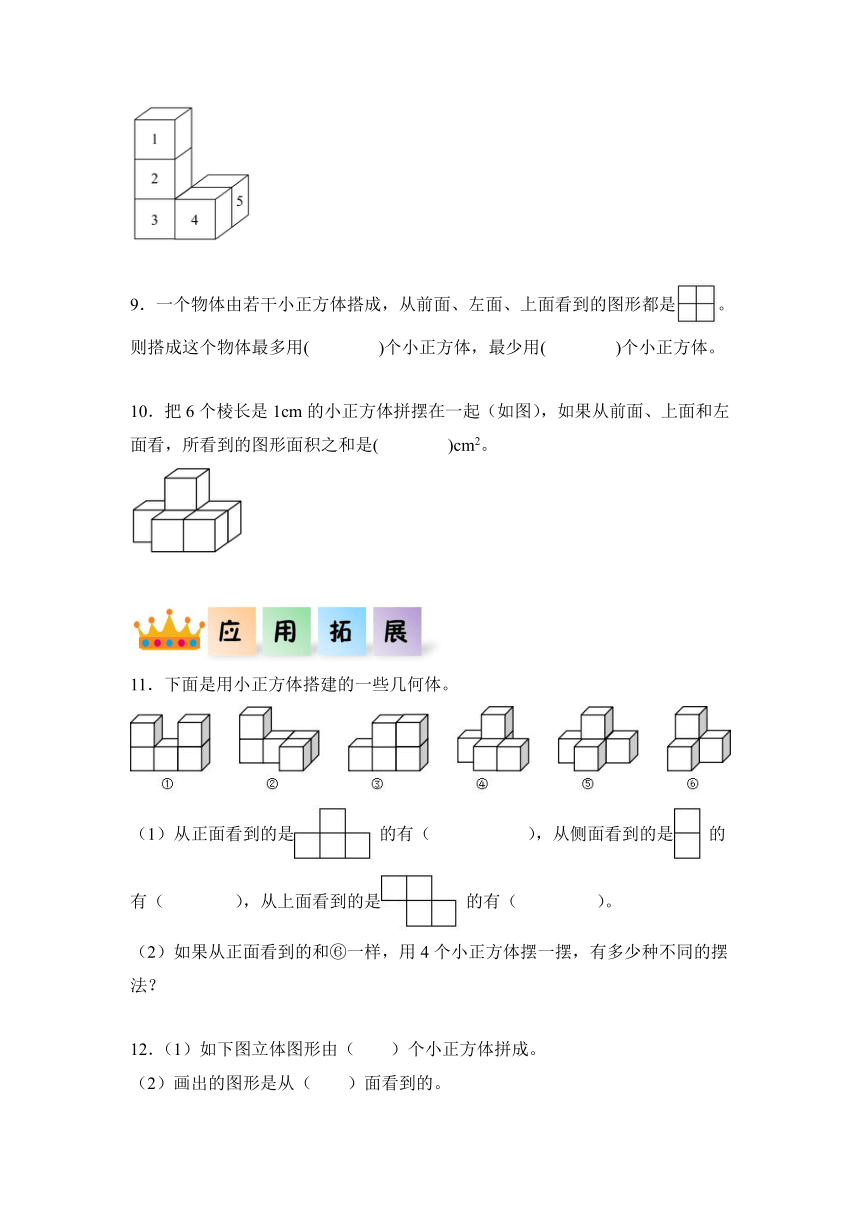
5.(2023·西城期末)如果用□表示1个立方体,用表示两个立方体叠加,用■表示三个立方体叠加,那么下图由8个立方体叠加的几何体,从正面观察,可画出的平面图形是( )。
A. B. C. D.
6.(2023·北京海淀区期末)人们使用“盲人摸象”来形容那些观察事物片面,只见局部不见整体的人。数学学习上也存在这样的问题,比如用6个同样的小正方体摆图形,如果要求从正面看到的是,你能确定这6个小正方体是怎样摆的吗?( )(选填“能”或“不能”)
7.如图:从( )面看是,从( )面看是,从( )面看是。
8.(2023·广州期末)如图的立体图形,要想从上面看形状不变,最多可以拿掉( )个小正方体。
9.一个物体由若干小正方体搭成,从前面、左面、上面看到的图形都是。则搭成这个物体最多用( )个小正方体,最少用( )个小正方体。
10.把6个棱长是1cm的小正方体拼摆在一起(如图),如果从前面、上面和左面看,所看到的图形面积之和是( )cm2。
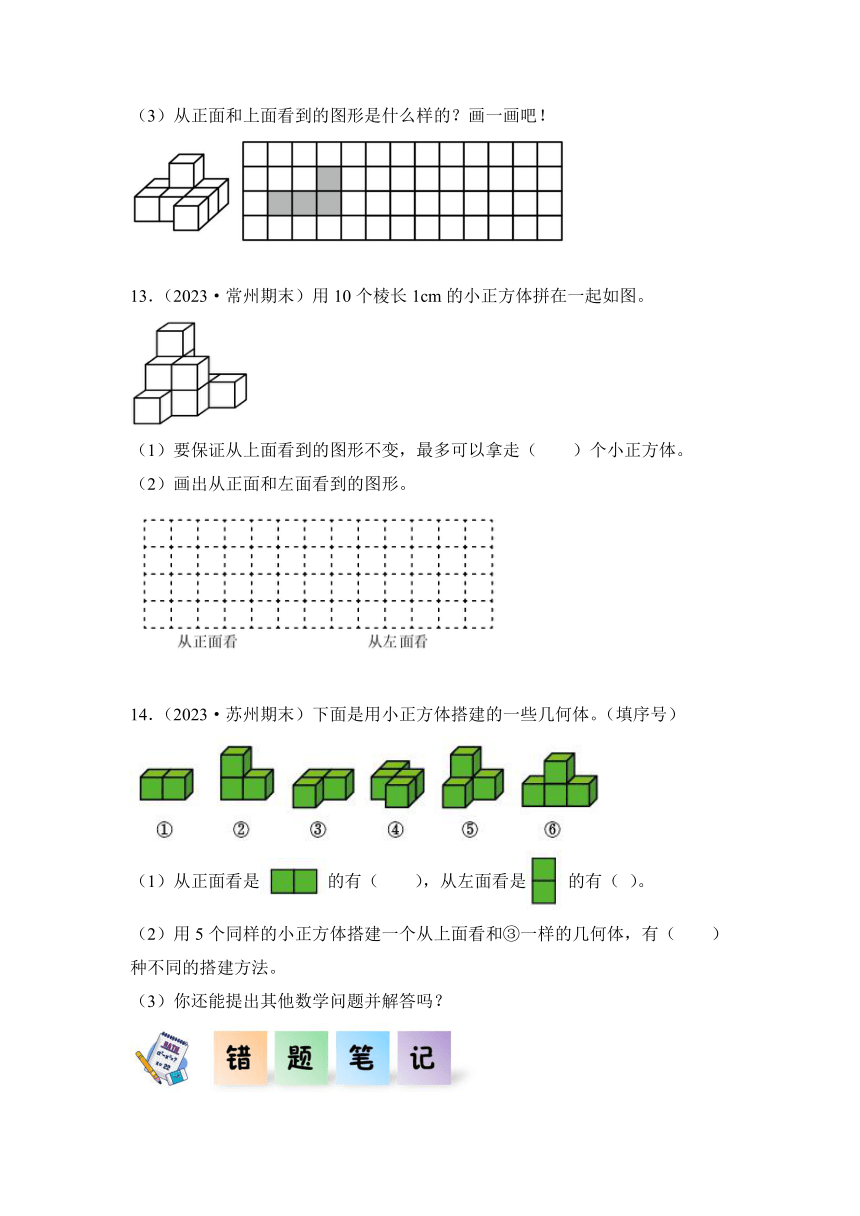
11.下面是用小正方体搭建的一些几何体。
(1)从正面看到的是的有( ),从侧面看到的是的有( ),从上面看到的是的有( )。
(2)如果从正面看到的和⑥一样,用4个小正方体摆一摆,有多少种不同的摆法?
12.(1)如下图立体图形由( )个小正方体拼成。
(2)画出的图形是从( )面看到的。
(3)从正面和上面看到的图形是什么样的?画一画吧!
13.(2023·常州期末)用10个棱长1cm的小正方体拼在一起如图。
(1)要保证从上面看到的图形不变,最多可以拿走( )个小正方体。
(2)画出从正面和左面看到的图形。
14.(2023·苏州期末)下面是用小正方体搭建的一些几何体。(填序号)
(1)从正面看是的有( ),从左面看是的有( )。
(2)用5个同样的小正方体搭建一个从上面看和③一样的几何体,有( )种不同的搭建方法。
(3)你还能提出其他数学问题并解答吗?
1.【详解】通过观察图像可知,从正面看到的形状是,从左面看到的形状是,从上面看到的形状是;
故答案为:A
2.【详解】由分析可知:
这个几何体从前面看是。
故答案为:C
3.【详解】A.从左面看到的图形是;
B.,从左面看到的图形是;
C.,从左面看到的图形是;
D.,从左面看到的图形是。
故答案为:C
4.【分析】观察图形可知,从前面看到的形状是;从上面看到的形状是;从左面看到的形状是;从右面看到的形状是;据此逐一分析各项即可。
A.从四个面看到的形状不同,原题干说法错误;
B.左面和右面看到的形状不相同,原题干说法错误;
C.前面和左面看到的形状不相同,原题干说法错误;
D.前面和右面看到的形状相同,原题干说法正确。
故答案为:D
5.【分析】根据题意可知,□表示1个立方体,用表示2个立方体叠加,用■表示3个立方体叠加,然后通过观察几何体正面即可分析解答。
【详解】通过观察图形可知,先从正面观察,一层是三个正方形一行,中间正方形上面有一个正方形,然后确定立方体叠加数量,一层左边有一个正方体是□,右边有两个正方体叠加是,中间一个是3个立方体的叠加是■,第二层是2个立方体的叠加是 。所以,从正面观察,可画出的平面图形是。
故答案为:A
6.不能
【分析】根据不同方向观察物体可知,6个同样的小正方体摆图形,如果要求从正面看到的是,会有多种摆放方法,不能确定这6个小正方体是怎样摆放的。如:前面5个小正方体如图示摆放,剩下1个小正方体可以放在底层从左往右数,第一个小正方体后面,也可以放在第二个小正方体后面,也可以放在第三个小正方体后面。据此解答即可。
【详解】如果要求从正面看到的是,不能确定这6个小正方体是怎样摆的。
7. 侧 正 上
【分析】观察立体图形,从侧面看到的图形有两层,第一层和第二层都有1个小正方形;从正面看到的图形有两行,三列,第一列和第二列都有2个小正方形,第三列有1个小正方形位于第2行;从上面看到的图形有1行,这行有3个小正方形。据此填空即可。
【详解】由分析可知:
从侧面看是,从正面看是,从上面看是。
8.2
【分析】题中图形从上面看到的正方形有两行,共3个小正方形,上面1个,下面2个,右对齐,并且每个小正方形叠加的数量如图:
据此分析解答即可。
【详解】由分析可得:
要使从上面的形状不变,最多可以将做左边叠加3个的正方体,拿走2个。
综上所述:如图的立体图形,要想从上面看形状不变,最多可以拿掉2个小正方体。
9. 8 6
【详解】根据题意,画图如下:
4+4=8(个)
4+2=6(个)
由此可知,搭成这个物体最多用8个小正方体,最少用6个小正方体。
10.12
【分析】观察图形可知,从前面能看到4个小正方形,从上面能看到5个小正方形,从左面能看到3个小正方形,则一共看到(4+5+3)个小正方形;
根据正方形的面积=边长×边长,求出一个面的面积,再乘从前面、上面和左面看到小正方形的个数即可。
【详解】1×1=1(cm2)
1×(4+5+3)
=1×12
=12(cm2)
如果从前面、上面和左面看,所看到的图形面积之和是12cm2。
11.(1)④⑤;①③;④
(2)5
【分析】(1)从正面看到的是二行,最下面一行三个小正方形并排,上面一行一个放在中间;从侧面看是一列两个,上下排列;从上面看是二行三列,上下行各两个正方形,呈“Z”型排列。由此分析判断。
(2)几何体⑥从正面看到的形状如右: ,根据此图,展开想象,确定物体的形状。
【详解】(1)从正面看到的是的有(④⑤),从侧面看到的是的有(①③),从上面看到的是的有(④)。
(2)如果从正面看到的和⑥一样,用4个小正方体摆一摆,可以有如下摆法。
共有5种。
12.(1)8
(2)右
(3)见详解
【分析】(1)观察立体图形,分两层,上层有1个小正方体,下层有7个小正方体,据此得解。
(2)观察平面图形,分两层共4个小正方形,下层3个,上层1个且居右,据此确定是从右面观察立体图形得到的这个平面图形。
(3)从正面能看到4个小正方形,分两层,上层1个且居中,下层3个;从上面能看到7个小正方形,分三层,上层、中层各3个,下层1个且居右;据此画出从正面和上面看到的图形。
【详解】(1)1+7=8(个)
立体图形由8个小正方体拼成。
(2)画出的图形是从右面看到的。
(3)如图:
13.(1)4
(2)见详解
【分析】(1)把第二层和第三层的正方体都去掉,从上面看到的图形不变;
(2)观察图形可知,从正面和左面看到的图形有三层,第一层有3个正方形,第二层有2个正方形,第三层有1个正方形,靠左齐;据此作图即可。
【详解】第二层有3个正方体,第三层有1个正方体
3+1=4(个)
则要保证从上面看到的图形不变,最多可以拿走4个小正方体。
(2)如图所示:
14.(1)①③④;②⑥;
(2)6;
(3)从( )面看④与从( )面看⑥的图形是一样的;
左或右;上(答案不唯一)
【分析】(1)假设自己是观察者,先按照题意站在不同方向看各几何体是什么形状,再把从不同方向观察到的平面图形进行分类填写。如果有困难,那么也可用积木摆一摆,看一看,再做判断。
(2)从上面看几何体③是,且几何体③用了3个小正方体。如果用5个小正方体摆,另外2个小正方体可以放在这3个小正方体的任意1个或2个上面,这样从上面看到的形状不变,由此解答即可。
(3)可提出从( )面看④与从( )面看⑥的图形是一样的。
【详解】(1)从正面看,只有一层且这层只有2个小正方形的几何体有①③④;从左面看,有两层且每层只有1个小正方形的几何体有②⑥;
(2)如图:
(3)从左(或右)面看④与从上面看⑥的图形是一样的。
1.是从的( )面看到的形状。
A.上 B.正 C.左
2.(2023·南京期末)用同样的小正方体搭一个几何体,从上面看到的图形如下图(每个正方形上面的数字表示在这个位置上所用的小正方体的个数)。这个几何体从前面看是( )。
A. B. C. D.
3.从左面看到的图形是的是( )。
A. B. C. D.
4.(2023·常州期末)从前面、上面、左面和右面观察下面的几何体,关于看到的形状描述正确的是( )。
A.四个面看到的形状相同 B.左面和右面看到的形状相同
C.前面和左面看到的形状相同 D.前面和右面看到的形状相同
5.(2023·西城期末)如果用□表示1个立方体,用表示两个立方体叠加,用■表示三个立方体叠加,那么下图由8个立方体叠加的几何体,从正面观察,可画出的平面图形是( )。
A. B. C. D.
6.(2023·北京海淀区期末)人们使用“盲人摸象”来形容那些观察事物片面,只见局部不见整体的人。数学学习上也存在这样的问题,比如用6个同样的小正方体摆图形,如果要求从正面看到的是,你能确定这6个小正方体是怎样摆的吗?( )(选填“能”或“不能”)
7.如图:从( )面看是,从( )面看是,从( )面看是。
8.(2023·广州期末)如图的立体图形,要想从上面看形状不变,最多可以拿掉( )个小正方体。
9.一个物体由若干小正方体搭成,从前面、左面、上面看到的图形都是。则搭成这个物体最多用( )个小正方体,最少用( )个小正方体。
10.把6个棱长是1cm的小正方体拼摆在一起(如图),如果从前面、上面和左面看,所看到的图形面积之和是( )cm2。
11.下面是用小正方体搭建的一些几何体。
(1)从正面看到的是的有( ),从侧面看到的是的有( ),从上面看到的是的有( )。
(2)如果从正面看到的和⑥一样,用4个小正方体摆一摆,有多少种不同的摆法?
12.(1)如下图立体图形由( )个小正方体拼成。
(2)画出的图形是从( )面看到的。
(3)从正面和上面看到的图形是什么样的?画一画吧!
13.(2023·常州期末)用10个棱长1cm的小正方体拼在一起如图。
(1)要保证从上面看到的图形不变,最多可以拿走( )个小正方体。
(2)画出从正面和左面看到的图形。
14.(2023·苏州期末)下面是用小正方体搭建的一些几何体。(填序号)
(1)从正面看是的有( ),从左面看是的有( )。
(2)用5个同样的小正方体搭建一个从上面看和③一样的几何体,有( )种不同的搭建方法。
(3)你还能提出其他数学问题并解答吗?
1.【详解】通过观察图像可知,从正面看到的形状是,从左面看到的形状是,从上面看到的形状是;
故答案为:A
2.【详解】由分析可知:
这个几何体从前面看是。
故答案为:C
3.【详解】A.从左面看到的图形是;
B.,从左面看到的图形是;
C.,从左面看到的图形是;
D.,从左面看到的图形是。
故答案为:C
4.【分析】观察图形可知,从前面看到的形状是;从上面看到的形状是;从左面看到的形状是;从右面看到的形状是;据此逐一分析各项即可。
A.从四个面看到的形状不同,原题干说法错误;
B.左面和右面看到的形状不相同,原题干说法错误;
C.前面和左面看到的形状不相同,原题干说法错误;
D.前面和右面看到的形状相同,原题干说法正确。
故答案为:D
5.【分析】根据题意可知,□表示1个立方体,用表示2个立方体叠加,用■表示3个立方体叠加,然后通过观察几何体正面即可分析解答。
【详解】通过观察图形可知,先从正面观察,一层是三个正方形一行,中间正方形上面有一个正方形,然后确定立方体叠加数量,一层左边有一个正方体是□,右边有两个正方体叠加是,中间一个是3个立方体的叠加是■,第二层是2个立方体的叠加是 。所以,从正面观察,可画出的平面图形是。
故答案为:A
6.不能
【分析】根据不同方向观察物体可知,6个同样的小正方体摆图形,如果要求从正面看到的是,会有多种摆放方法,不能确定这6个小正方体是怎样摆放的。如:前面5个小正方体如图示摆放,剩下1个小正方体可以放在底层从左往右数,第一个小正方体后面,也可以放在第二个小正方体后面,也可以放在第三个小正方体后面。据此解答即可。
【详解】如果要求从正面看到的是,不能确定这6个小正方体是怎样摆的。
7. 侧 正 上
【分析】观察立体图形,从侧面看到的图形有两层,第一层和第二层都有1个小正方形;从正面看到的图形有两行,三列,第一列和第二列都有2个小正方形,第三列有1个小正方形位于第2行;从上面看到的图形有1行,这行有3个小正方形。据此填空即可。
【详解】由分析可知:
从侧面看是,从正面看是,从上面看是。
8.2
【分析】题中图形从上面看到的正方形有两行,共3个小正方形,上面1个,下面2个,右对齐,并且每个小正方形叠加的数量如图:
据此分析解答即可。
【详解】由分析可得:
要使从上面的形状不变,最多可以将做左边叠加3个的正方体,拿走2个。
综上所述:如图的立体图形,要想从上面看形状不变,最多可以拿掉2个小正方体。
9. 8 6
【详解】根据题意,画图如下:
4+4=8(个)
4+2=6(个)
由此可知,搭成这个物体最多用8个小正方体,最少用6个小正方体。
10.12
【分析】观察图形可知,从前面能看到4个小正方形,从上面能看到5个小正方形,从左面能看到3个小正方形,则一共看到(4+5+3)个小正方形;
根据正方形的面积=边长×边长,求出一个面的面积,再乘从前面、上面和左面看到小正方形的个数即可。
【详解】1×1=1(cm2)
1×(4+5+3)
=1×12
=12(cm2)
如果从前面、上面和左面看,所看到的图形面积之和是12cm2。
11.(1)④⑤;①③;④
(2)5
【分析】(1)从正面看到的是二行,最下面一行三个小正方形并排,上面一行一个放在中间;从侧面看是一列两个,上下排列;从上面看是二行三列,上下行各两个正方形,呈“Z”型排列。由此分析判断。
(2)几何体⑥从正面看到的形状如右: ,根据此图,展开想象,确定物体的形状。
【详解】(1)从正面看到的是的有(④⑤),从侧面看到的是的有(①③),从上面看到的是的有(④)。
(2)如果从正面看到的和⑥一样,用4个小正方体摆一摆,可以有如下摆法。
共有5种。
12.(1)8
(2)右
(3)见详解
【分析】(1)观察立体图形,分两层,上层有1个小正方体,下层有7个小正方体,据此得解。
(2)观察平面图形,分两层共4个小正方形,下层3个,上层1个且居右,据此确定是从右面观察立体图形得到的这个平面图形。
(3)从正面能看到4个小正方形,分两层,上层1个且居中,下层3个;从上面能看到7个小正方形,分三层,上层、中层各3个,下层1个且居右;据此画出从正面和上面看到的图形。
【详解】(1)1+7=8(个)
立体图形由8个小正方体拼成。
(2)画出的图形是从右面看到的。
(3)如图:
13.(1)4
(2)见详解
【分析】(1)把第二层和第三层的正方体都去掉,从上面看到的图形不变;
(2)观察图形可知,从正面和左面看到的图形有三层,第一层有3个正方形,第二层有2个正方形,第三层有1个正方形,靠左齐;据此作图即可。
【详解】第二层有3个正方体,第三层有1个正方体
3+1=4(个)
则要保证从上面看到的图形不变,最多可以拿走4个小正方体。
(2)如图所示:
14.(1)①③④;②⑥;
(2)6;
(3)从( )面看④与从( )面看⑥的图形是一样的;
左或右;上(答案不唯一)
【分析】(1)假设自己是观察者,先按照题意站在不同方向看各几何体是什么形状,再把从不同方向观察到的平面图形进行分类填写。如果有困难,那么也可用积木摆一摆,看一看,再做判断。
(2)从上面看几何体③是,且几何体③用了3个小正方体。如果用5个小正方体摆,另外2个小正方体可以放在这3个小正方体的任意1个或2个上面,这样从上面看到的形状不变,由此解答即可。
(3)可提出从( )面看④与从( )面看⑥的图形是一样的。
【详解】(1)从正面看,只有一层且这层只有2个小正方形的几何体有①③④;从左面看,有两层且每层只有1个小正方形的几何体有②⑥;
(2)如图:
(3)从左(或右)面看④与从上面看⑥的图形是一样的。
