河北省邯郸市第二十五中学2024-2025学年八年级下学期期中考试数学试卷(含答案)
文档属性
| 名称 | 河北省邯郸市第二十五中学2024-2025学年八年级下学期期中考试数学试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 00:00:00 | ||
图片预览


文档简介
河北省邯郸市第二十五中学2024-2025学年八年级下学期期中考试数学试卷
一、单选题
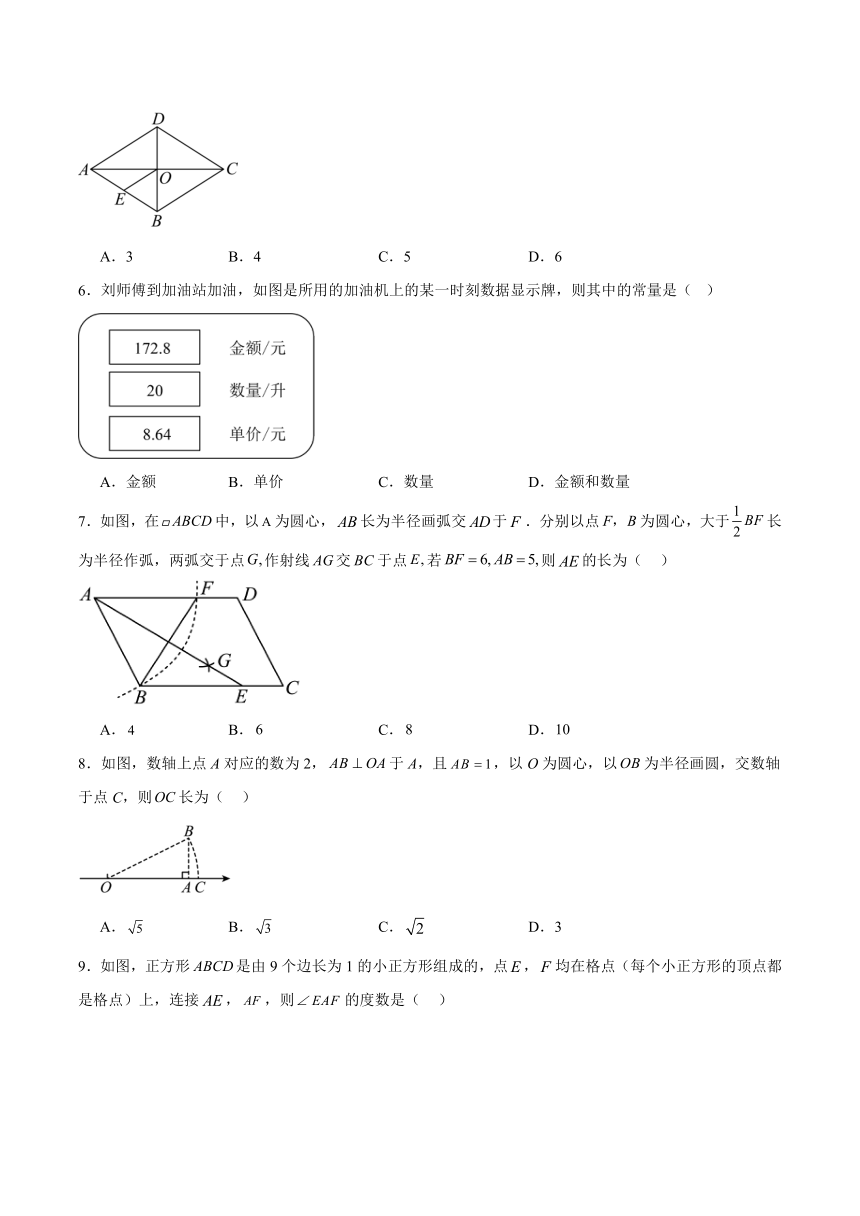
1.函数中,自变量x的取值范围是( )
A. B.
C. D.或
2.在平面直角坐标系中,点,则点P到原点的距离为( )
A.3 B. C.5 D.4
3.如图,M,N分别是的边AB,AC的中点,若,则=( )
A. B. C. D.
4.以下是长沙某日气温变化情况的折线图,下列描述正确的是( )
A.最低温度是 B.最高温度是
C.从0时到14时温度在持续上升 D.这一天的最大温差是
5.如图,菱形的对角线,相交于点,是边的中点,连接,若,则菱形的边长为( )
A.3 B.4 C.5 D.6
6.刘师傅到加油站加油,如图是所用的加油机上的某一时刻数据显示牌,则其中的常量是( )
A.金额 B.单价 C.数量 D.金额和数量
7.如图,在中,以为圆心,长为半径画弧交于.分别以点为圆心,大于长为半径作弧,两弧交于点作射线交于点若则的长为( )
A. B. C. D.
8.如图,数轴上点A对应的数为2,于A,且,以O为圆心,以为半径画圆,交数轴于点C,则长为( )
A. B. C. D.3
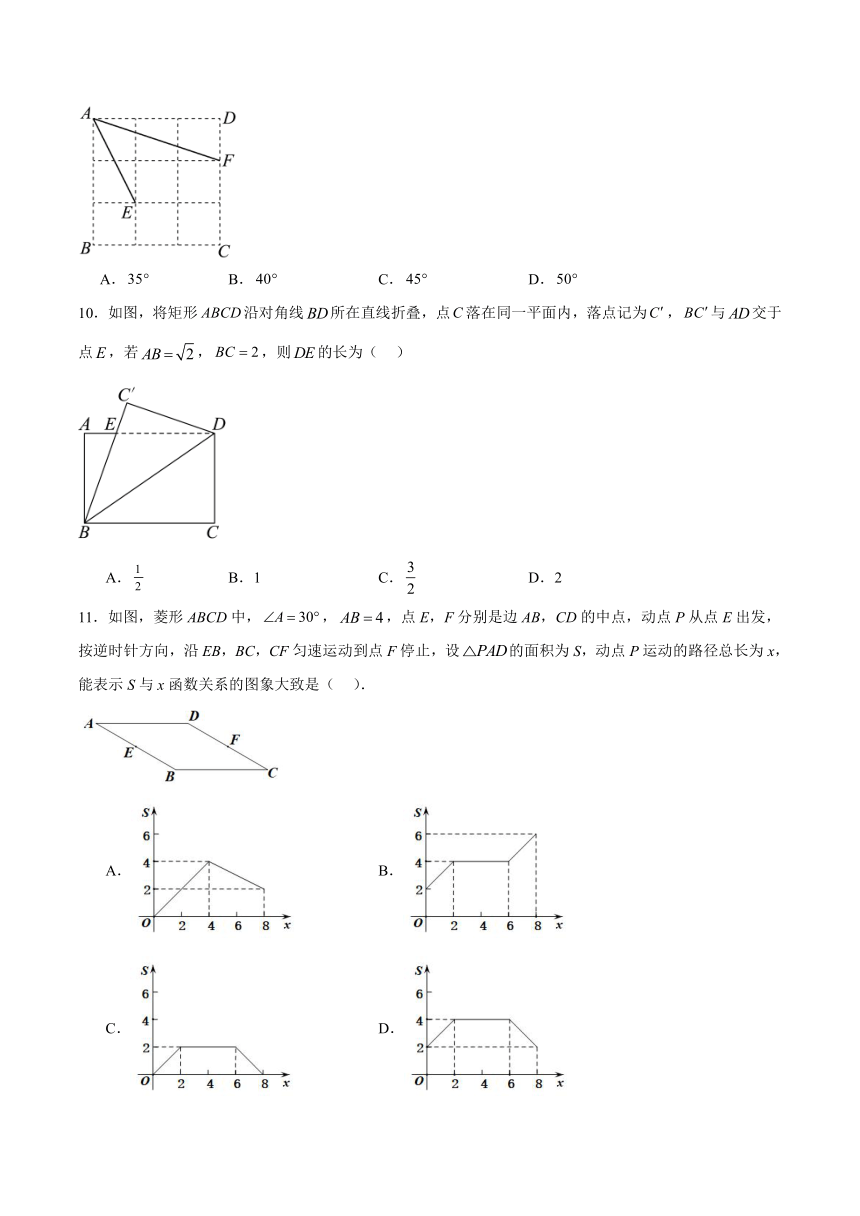
9.如图,正方形是由9个边长为1的小正方形组成的,点,均在格点(每个小正方形的顶点都是格点)上,连接,,则的度数是( )
A. B. C. D.
10.如图,将矩形沿对角线所在直线折叠,点落在同一平面内,落点记为,与交于点,若,,则的长为( )
A. B.1 C. D.2
11.如图,菱形ABCD中,,,点E,F分别是边AB,CD的中点,动点P从点E出发,按逆时针方向,沿EB,BC,CF匀速运动到点F停止,设的面积为S,动点P运动的路径总长为x,能表示S与x函数关系的图象大致是( ).
A. B.
C. D.
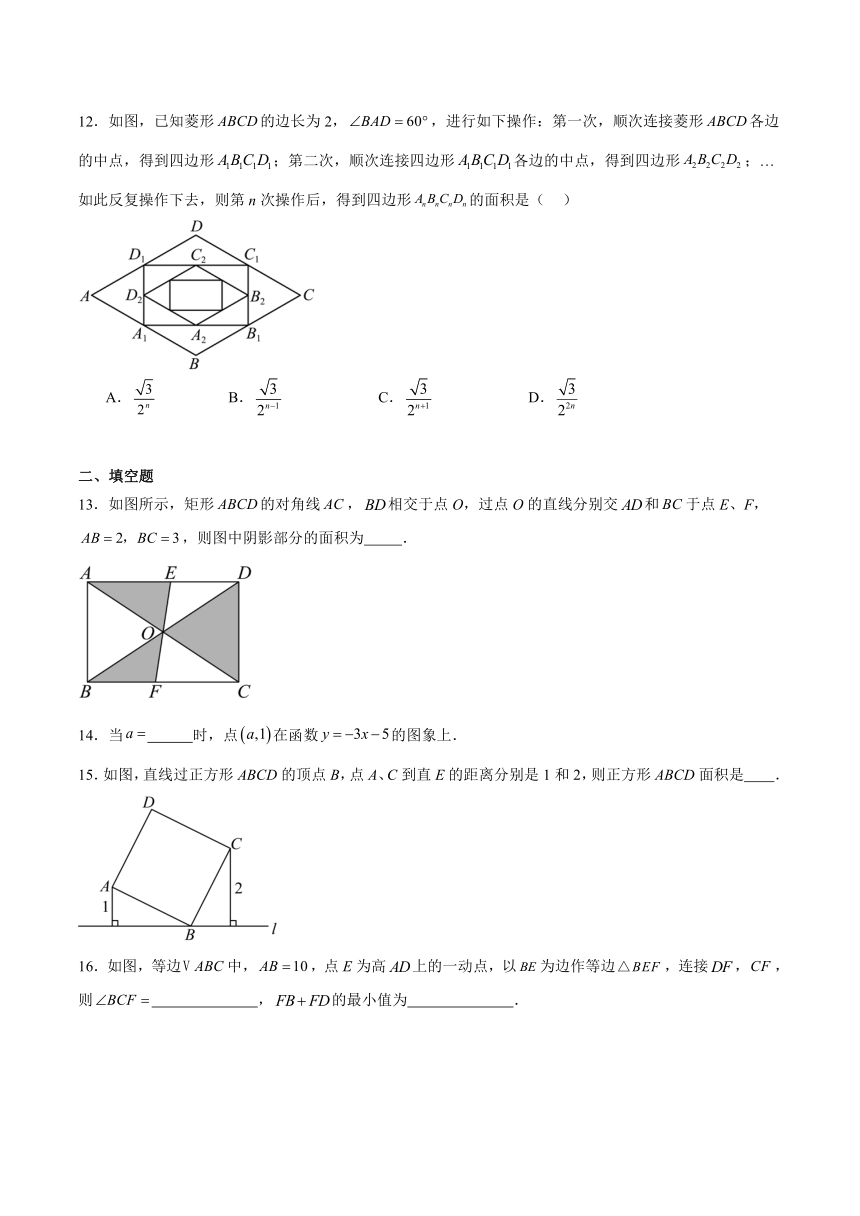
12.如图,已知菱形的边长为2,,进行如下操作:第一次,顺次连接菱形各边的中点,得到四边形;第二次,顺次连接四边形各边的中点,得到四边形;…如此反复操作下去,则第n次操作后,得到四边形的面积是( )
A. B. C. D.
二、填空题
13.如图所示,矩形的对角线,相交于点O,过点O的直线分别交和于点E、F,,则图中阴影部分的面积为 .
14.当 时,点在函数的图象上.
15.如图,直线过正方形ABCD的顶点B,点A、C到直E的距离分别是1和2,则正方形ABCD面积是 .
16.如图,等边中,,点E为高上的一动点,以为边作等边,连接,,则 ,的最小值为 .
三、解答题
17.已知.
(1)若把y看成是x的函数关系式,求出其函数关系式;
(2)当或时,求函数值;
(3)当时,求自变量x的值.
18.周老师在一次“探究性学习”课中,设计了如下数表:
n 2 3 4 5 …
a …
b 4 6 8 10 …
c …
(1)请你分别观察a、b、c与n之间的关系,并用含自然数的代数式表示;
(2)猜想:以a、b、c为边的三角形是否为直角三角形?请证明你的猜想.
19.已知琳琳家、药店、邮局在同一直线上,琳琳从家出发,跑步去药店买了酒精和口罩,又步行到邮局把物品寄出,然后走回家.琳琳离家的距离y(km)与时间x(min)之间的关系如图所示,请根据图象解决下列问题:
(1)琳琳家离药店的距离为________km;
(2)琳琳邮寄物品用了________min;
(3)求琳琳从邮局走回家的速度是多少?
20.如图,在 ABCD中,对角线AC,BD交于点O,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)求证:EO=FO;
(2)若AE=EF=4,求AC的长.
21.小明学习小组在活动课上进行了项目式学习实践探究,并绘制了如下记录表格:
课题 利用旗杆的拉绳测量学校旗杆的高度
模型抽象
测绘数据 ①绳子紧贴着旗杆垂直向下,再把多余的绳子拉直,测得多余的绳子长度为.
②拉直绳子,使绳子末端C刚好与地面上的点D重合,测量旗杆底部点B到绳子终点D的距离,即.
说明 点A,B,D在同一平面上.
请根据表格信息,解答下列问题.(,)
(1)求旗杆的高度的长.
(2)由于实际需要,现在要把旗杆增高,如果绳子还能拉到点D处,则绳子至少要加长多少米?(结果保留一位小数).
22.如图,在菱形中,分别是边的中点,连接并延长,交的延长线于点.
(1)求证:;
(2)若,,求的长.
23.如图所示,在四边形中,,,,点P从A向点D以的速度运动,到点D即停止.点Q从点C向点B以的速度运动,到点B即停止,直线将四边形截得两个四边形,分别为四边形和四边形,
(1)则当P,Q两点同时出发,几秒后所截得两个四边形中,其中一个四边形为平行四边形?
(2)若,当时,直接写出经过______秒后,.
24.定义:有一个内角为,且对角线相等的四边形称为准矩形.
(1)①如图1,准矩形中,,若,,则_____;
②如图2,直角坐标系中,,,若整点使得四边形是准矩形,则点的坐标是_____;(整点指横坐标、纵坐标都为整数的点)
(2)如图3,正方形中,点、分别是边、上的点,且,求证:四边形是准矩形;
(3)已知,准矩形中,,,,当是以为腰的等腰三角形时,请直接写出这个准矩形的面积是_____.
参考答案
1.B
解:由题意,得:,
解得:,
故选B.
2.C
解:点,
点到原点的距离是:.
故选:C.
3.D
解:∵M,N分别是的边AB,AC的中点,
∴MN∥BC,
∴∠ANM=∠C,
∵,
∴,
又∵
∴,
故选:D.
4.B
解:最低温度是,故选项A错误;
最高温度是,故选项B正确;
从时到14时温度在持续上升,故选项C错误;
这一天的最大温差是,故选项D错误;
故选B.
5.D
解:∵四边形是菱形,
,
是边的中点,
,
,
即菱形的边长为6,
故选:D.
6.B
解:由题意,可知,石油的单价为定值,固定不变,金额随着数量的变化而变化,
故常量为单价;
故选B.
7.C
如下图,AE与BF交于点O,连接EF
由作图可知,AE与BF相互垂直平分
∵BF=6,∴BO=3
∵AB=5
∴在Rt△ABO中,AO=4
∴AE=8
故选:C.
8.A
解:在直角中,.
.
.
故选:A.
9.C
解:如图所示,连接,
根据勾股定理,得,.
∵,
∴,
∴是等腰直角三角形,
∴,
故选C.
10.C
∵四边形是矩形,
∴,,,
∴,
由折叠得,
∴,
∴,
在中,,,,
∴,
解得,.
故选:C.
11.D
解:在菱形ABCD中:,
∵点E,F分别是边AB,CD的中点,
∴.
当P在EB上时, 时,过点P作PH⊥AD于点H,则,,
∵∠A=30°,
∴,
∴,
∴此时图象是与y轴交于 的线段;
当P在BC上时, 时,过点B作BM⊥AD于点M,则,
∵∠A=30°,
∴,
∴,
∵,
∴,
∴此时图象是平行于x轴的线段;
当P在CF上时, 时,过点P作PN⊥AD于点N,则,,
∴,
∵∠A=30°,,
∴ ,
∴,
∴S=,
∴此时图象是一条过 的线段;
观察四个选项,只有选项D符合题意,
故选:D.
12.B
解:连接,,,,
∵四边形为菱形,
∴,,,,
∴,
∵,
∴为等边三角形,
∴,
∴,
∴,
∴,
∴,
∵第一次,顺次连接菱形各边的中点,得到四边形,
∴,,,,
∴四边形为平行四边形,
∵,,
∴,
∵,
∴,
∴四边形为矩形,
∴,
∴,
∵第二次,顺次连接四边形各边的中点,得到四边形,
∴,,,
∴,
∴四边形为菱形,
∴,
依次可得,,
故选:B.
13.3
解:∵四边形是矩形,
∴,
∴.
∵,
∴,
∴,
∴阴影部分的面积为,
∴,
∴阴影部分的面积为3,
故答案为:3.
14.
解:因为点在函数的图像上,
所以,
解得.
故答案为:.
15.5.
解:如图,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∵AE⊥EF,CF⊥EF,
∴∠AEB=∠BFC=90°,
∴∠ABE+∠CBF=180°-90°=90°,∠ABE+∠EAB=90°,
∴∠EAB=∠CBF,
在△AEB和△BFC中,
,
∴△AEB≌△BFC(AAS),
∴BE=CF=2,
在Rt△AEB中,由勾股定理得: ,
即正方形ABCD的面积是5,
故答案为:5.
16. /30度
解:①∵为等边三角形,
∴,,
∴,
∵是等边三角形,
∵,,
∴,
,
∴,
在和中
∴,
得;
故答案为:.
②(将军饮马问题)
过点D作定直线CF的对称点G,连CG,
∴为等边三角形,为的中垂线,,
∴,
连接,
∴,
又,
∴为直角三角形,
∵,,
∴,
∴的最小值为.
故答案为:.
17.(1)
(2)1或
(3)7
(1)解:移项,得,
两边都除以2,得;
(2)解:当时,;
当时,;
(3)解:当时,,
解得.
18.(1)
(2)是,理由见解析
(1)由图表可以得出:
∵时,,
时,,
时,,
…,
∴;
(2)以a,b,c为边长的三角形是直角三角形.理由如下:
∵,
,
∴,
∴以a、b、c为边的三角形是直角三角形.
19.(1)2.5;
(2)20;
(3)
(1)由图象可知,琳琳家离药店的距离为,
故答案为:2.5;
(2)由图象可知,琳琳邮寄物品用了:(分钟),
故答案为:20;
(3)从邮局步行回家的路程为,时间为,所以速度为:.
20.(1)见解析;(2).
(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥ED,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴,
∴BE=DF,
∵OB=OD,
∴OB-BE=OD-DF,
∴OE=OF.
(2)∵AE=EF=4,
∴OE=OF=,
∴在中,,
∴.
21.(1)
(2)
(1)解:由题意得,,
设,则,
又,
在中,,
∴,
解得,
答:旗杆的长为.
(2)解:由(1)得,延长至点,使,连接
则
在中,,
则绳子至少要加长:,
答:绳子至少要加长.
22.(1)证明见解析
(2)
(1)证明:连接,交交于,如图所示:
∵四边形是菱形,
∴,
∵分别是边的中点,
∴,
∴;
(2)解:∵,,
∴四边形是平行四边形,
∴,
在中,,,,则由勾股定理可得,
∴,
∴.
23.(1)8或10
(2)8或12
(1)解:设运动时间为t秒,可知,则
当时,四边形是平行四边形,即,
解得;
当时,四边形是平行四边形,即,
解得.
所以当时间为8秒或10秒时,其中一个四边形是平行四边形;
(2)解:如图所示,过点D作,交于点E,
根据题意可知四边形是矩形,
∴,
∴.
在中,,
解得.
如图所示四边形是等腰梯形或平行四边形,即,此时,
即,
解得或,
所以当或时,.
故答案为:8或12.
24.(1)①;②或;
(2)证明见解析;
(3)或
(1)解:①,
,
故答案为:,
②,,
,
设点,,
,
,都为整数,
点或;
故答案为:或;
(2)解:四边形是正方形,
,,
,
,
,
,
,
,
四边形是准矩形;
(3)解:,,,
,
准矩形中,,
①当时,如图1,作,
,
,
;
②当时,如图2,
作,
∵,
,
,
;
故答案为:或
一、单选题
1.函数中,自变量x的取值范围是( )
A. B.
C. D.或
2.在平面直角坐标系中,点,则点P到原点的距离为( )
A.3 B. C.5 D.4
3.如图,M,N分别是的边AB,AC的中点,若,则=( )
A. B. C. D.
4.以下是长沙某日气温变化情况的折线图,下列描述正确的是( )
A.最低温度是 B.最高温度是
C.从0时到14时温度在持续上升 D.这一天的最大温差是
5.如图,菱形的对角线,相交于点,是边的中点,连接,若,则菱形的边长为( )
A.3 B.4 C.5 D.6
6.刘师傅到加油站加油,如图是所用的加油机上的某一时刻数据显示牌,则其中的常量是( )
A.金额 B.单价 C.数量 D.金额和数量
7.如图,在中,以为圆心,长为半径画弧交于.分别以点为圆心,大于长为半径作弧,两弧交于点作射线交于点若则的长为( )
A. B. C. D.
8.如图,数轴上点A对应的数为2,于A,且,以O为圆心,以为半径画圆,交数轴于点C,则长为( )
A. B. C. D.3
9.如图,正方形是由9个边长为1的小正方形组成的,点,均在格点(每个小正方形的顶点都是格点)上,连接,,则的度数是( )
A. B. C. D.
10.如图,将矩形沿对角线所在直线折叠,点落在同一平面内,落点记为,与交于点,若,,则的长为( )
A. B.1 C. D.2
11.如图,菱形ABCD中,,,点E,F分别是边AB,CD的中点,动点P从点E出发,按逆时针方向,沿EB,BC,CF匀速运动到点F停止,设的面积为S,动点P运动的路径总长为x,能表示S与x函数关系的图象大致是( ).
A. B.
C. D.
12.如图,已知菱形的边长为2,,进行如下操作:第一次,顺次连接菱形各边的中点,得到四边形;第二次,顺次连接四边形各边的中点,得到四边形;…如此反复操作下去,则第n次操作后,得到四边形的面积是( )
A. B. C. D.
二、填空题
13.如图所示,矩形的对角线,相交于点O,过点O的直线分别交和于点E、F,,则图中阴影部分的面积为 .
14.当 时,点在函数的图象上.
15.如图,直线过正方形ABCD的顶点B,点A、C到直E的距离分别是1和2,则正方形ABCD面积是 .
16.如图,等边中,,点E为高上的一动点,以为边作等边,连接,,则 ,的最小值为 .
三、解答题
17.已知.
(1)若把y看成是x的函数关系式,求出其函数关系式;
(2)当或时,求函数值;
(3)当时,求自变量x的值.
18.周老师在一次“探究性学习”课中,设计了如下数表:
n 2 3 4 5 …
a …
b 4 6 8 10 …
c …
(1)请你分别观察a、b、c与n之间的关系,并用含自然数的代数式表示;
(2)猜想:以a、b、c为边的三角形是否为直角三角形?请证明你的猜想.
19.已知琳琳家、药店、邮局在同一直线上,琳琳从家出发,跑步去药店买了酒精和口罩,又步行到邮局把物品寄出,然后走回家.琳琳离家的距离y(km)与时间x(min)之间的关系如图所示,请根据图象解决下列问题:
(1)琳琳家离药店的距离为________km;
(2)琳琳邮寄物品用了________min;
(3)求琳琳从邮局走回家的速度是多少?
20.如图,在 ABCD中,对角线AC,BD交于点O,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)求证:EO=FO;
(2)若AE=EF=4,求AC的长.
21.小明学习小组在活动课上进行了项目式学习实践探究,并绘制了如下记录表格:
课题 利用旗杆的拉绳测量学校旗杆的高度
模型抽象
测绘数据 ①绳子紧贴着旗杆垂直向下,再把多余的绳子拉直,测得多余的绳子长度为.
②拉直绳子,使绳子末端C刚好与地面上的点D重合,测量旗杆底部点B到绳子终点D的距离,即.
说明 点A,B,D在同一平面上.
请根据表格信息,解答下列问题.(,)
(1)求旗杆的高度的长.
(2)由于实际需要,现在要把旗杆增高,如果绳子还能拉到点D处,则绳子至少要加长多少米?(结果保留一位小数).
22.如图,在菱形中,分别是边的中点,连接并延长,交的延长线于点.
(1)求证:;
(2)若,,求的长.
23.如图所示,在四边形中,,,,点P从A向点D以的速度运动,到点D即停止.点Q从点C向点B以的速度运动,到点B即停止,直线将四边形截得两个四边形,分别为四边形和四边形,
(1)则当P,Q两点同时出发,几秒后所截得两个四边形中,其中一个四边形为平行四边形?
(2)若,当时,直接写出经过______秒后,.
24.定义:有一个内角为,且对角线相等的四边形称为准矩形.
(1)①如图1,准矩形中,,若,,则_____;
②如图2,直角坐标系中,,,若整点使得四边形是准矩形,则点的坐标是_____;(整点指横坐标、纵坐标都为整数的点)
(2)如图3,正方形中,点、分别是边、上的点,且,求证:四边形是准矩形;
(3)已知,准矩形中,,,,当是以为腰的等腰三角形时,请直接写出这个准矩形的面积是_____.
参考答案
1.B
解:由题意,得:,
解得:,
故选B.
2.C
解:点,
点到原点的距离是:.
故选:C.
3.D
解:∵M,N分别是的边AB,AC的中点,
∴MN∥BC,
∴∠ANM=∠C,
∵,
∴,
又∵
∴,
故选:D.
4.B
解:最低温度是,故选项A错误;
最高温度是,故选项B正确;
从时到14时温度在持续上升,故选项C错误;
这一天的最大温差是,故选项D错误;
故选B.
5.D
解:∵四边形是菱形,
,
是边的中点,
,
,
即菱形的边长为6,
故选:D.
6.B
解:由题意,可知,石油的单价为定值,固定不变,金额随着数量的变化而变化,
故常量为单价;
故选B.
7.C
如下图,AE与BF交于点O,连接EF
由作图可知,AE与BF相互垂直平分
∵BF=6,∴BO=3
∵AB=5
∴在Rt△ABO中,AO=4
∴AE=8
故选:C.
8.A
解:在直角中,.
.
.
故选:A.
9.C
解:如图所示,连接,
根据勾股定理,得,.
∵,
∴,
∴是等腰直角三角形,
∴,
故选C.
10.C
∵四边形是矩形,
∴,,,
∴,
由折叠得,
∴,
∴,
在中,,,,
∴,
解得,.
故选:C.
11.D
解:在菱形ABCD中:,
∵点E,F分别是边AB,CD的中点,
∴.
当P在EB上时, 时,过点P作PH⊥AD于点H,则,,
∵∠A=30°,
∴,
∴,
∴此时图象是与y轴交于 的线段;
当P在BC上时, 时,过点B作BM⊥AD于点M,则,
∵∠A=30°,
∴,
∴,
∵,
∴,
∴此时图象是平行于x轴的线段;
当P在CF上时, 时,过点P作PN⊥AD于点N,则,,
∴,
∵∠A=30°,,
∴ ,
∴,
∴S=,
∴此时图象是一条过 的线段;
观察四个选项,只有选项D符合题意,
故选:D.
12.B
解:连接,,,,
∵四边形为菱形,
∴,,,,
∴,
∵,
∴为等边三角形,
∴,
∴,
∴,
∴,
∴,
∵第一次,顺次连接菱形各边的中点,得到四边形,
∴,,,,
∴四边形为平行四边形,
∵,,
∴,
∵,
∴,
∴四边形为矩形,
∴,
∴,
∵第二次,顺次连接四边形各边的中点,得到四边形,
∴,,,
∴,
∴四边形为菱形,
∴,
依次可得,,
故选:B.
13.3
解:∵四边形是矩形,
∴,
∴.
∵,
∴,
∴,
∴阴影部分的面积为,
∴,
∴阴影部分的面积为3,
故答案为:3.
14.
解:因为点在函数的图像上,
所以,
解得.
故答案为:.
15.5.
解:如图,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∵AE⊥EF,CF⊥EF,
∴∠AEB=∠BFC=90°,
∴∠ABE+∠CBF=180°-90°=90°,∠ABE+∠EAB=90°,
∴∠EAB=∠CBF,
在△AEB和△BFC中,
,
∴△AEB≌△BFC(AAS),
∴BE=CF=2,
在Rt△AEB中,由勾股定理得: ,
即正方形ABCD的面积是5,
故答案为:5.
16. /30度
解:①∵为等边三角形,
∴,,
∴,
∵是等边三角形,
∵,,
∴,
,
∴,
在和中
∴,
得;
故答案为:.
②(将军饮马问题)
过点D作定直线CF的对称点G,连CG,
∴为等边三角形,为的中垂线,,
∴,
连接,
∴,
又,
∴为直角三角形,
∵,,
∴,
∴的最小值为.
故答案为:.
17.(1)
(2)1或
(3)7
(1)解:移项,得,
两边都除以2,得;
(2)解:当时,;
当时,;
(3)解:当时,,
解得.
18.(1)
(2)是,理由见解析
(1)由图表可以得出:
∵时,,
时,,
时,,
…,
∴;
(2)以a,b,c为边长的三角形是直角三角形.理由如下:
∵,
,
∴,
∴以a、b、c为边的三角形是直角三角形.
19.(1)2.5;
(2)20;
(3)
(1)由图象可知,琳琳家离药店的距离为,
故答案为:2.5;
(2)由图象可知,琳琳邮寄物品用了:(分钟),
故答案为:20;
(3)从邮局步行回家的路程为,时间为,所以速度为:.
20.(1)见解析;(2).
(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABE=∠CDF,
∵AE⊥ED,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴,
∴BE=DF,
∵OB=OD,
∴OB-BE=OD-DF,
∴OE=OF.
(2)∵AE=EF=4,
∴OE=OF=,
∴在中,,
∴.
21.(1)
(2)
(1)解:由题意得,,
设,则,
又,
在中,,
∴,
解得,
答:旗杆的长为.
(2)解:由(1)得,延长至点,使,连接
则
在中,,
则绳子至少要加长:,
答:绳子至少要加长.
22.(1)证明见解析
(2)
(1)证明:连接,交交于,如图所示:
∵四边形是菱形,
∴,
∵分别是边的中点,
∴,
∴;
(2)解:∵,,
∴四边形是平行四边形,
∴,
在中,,,,则由勾股定理可得,
∴,
∴.
23.(1)8或10
(2)8或12
(1)解:设运动时间为t秒,可知,则
当时,四边形是平行四边形,即,
解得;
当时,四边形是平行四边形,即,
解得.
所以当时间为8秒或10秒时,其中一个四边形是平行四边形;
(2)解:如图所示,过点D作,交于点E,
根据题意可知四边形是矩形,
∴,
∴.
在中,,
解得.
如图所示四边形是等腰梯形或平行四边形,即,此时,
即,
解得或,
所以当或时,.
故答案为:8或12.
24.(1)①;②或;
(2)证明见解析;
(3)或
(1)解:①,
,
故答案为:,
②,,
,
设点,,
,
,都为整数,
点或;
故答案为:或;
(2)解:四边形是正方形,
,,
,
,
,
,
,
,
四边形是准矩形;
(3)解:,,,
,
准矩形中,,
①当时,如图1,作,
,
,
;
②当时,如图2,
作,
∵,
,
,
;
故答案为:或
同课章节目录
