2025年湖北省武汉市七一华源中学九年级下学期中考模拟数学试卷(含部分答案)
文档属性
| 名称 | 2025年湖北省武汉市七一华源中学九年级下学期中考模拟数学试卷(含部分答案) |  | |
| 格式 | docx | ||
| 文件大小 | 731.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 14:21:42 | ||
图片预览



文档简介
2024-2025学年度中考模拟九年级数学试题
一、选择题(本题共10小题,每小题3分,共30分)
1. 现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是( )
A. B. C. D.
2. 在下列事件中,必然事件是( )
A. 掷一次骰子,向上一面的点数是3
B. 篮球队员在罚球线上投篮一次,未投中
C. 经过有交通信号灯的路口,遇到红灯
D. 任意画一个三角形,其内角和180°
3. 如图是由4个相同的小正方体组成的几何体,它的主视图是( )
A. B.
C. D.
4. 国家统计局2024年4月16日发布数据,今年第一季度国内生产总值接近亿元,同比增长,国家高质量发展取得新成效.将数据用科学记数法表示是( )
A. B. C. D.
5. 下列运算正确的是( )
A. B.
C. D.
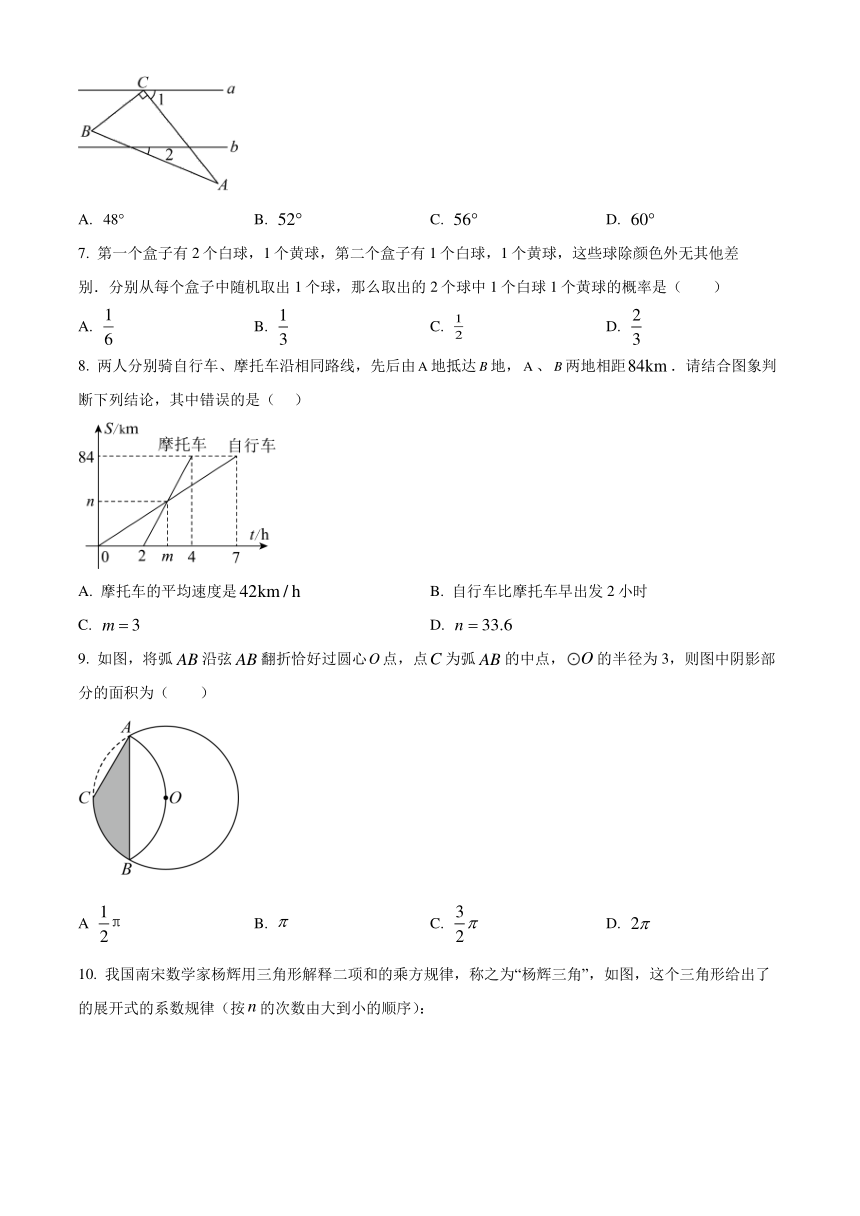
6. 如图,直线,的直角顶点在直线上,若,,则的度数为( )
A. B. C. D.
7. 第一个盒子有2个白球,1个黄球,第二个盒子有1个白球,1个黄球,这些球除颜色外无其他差别.分别从每个盒子中随机取出1个球,那么取出的2个球中1个白球1个黄球的概率是( )
A. B. C. D.
8. 两人分别骑自行车、摩托车沿相同路线,先后由地抵达地,、两地相距.请结合图象判断下列结论,其中错误的是( )
A. 摩托车的平均速度是 B. 自行车比摩托车早出发2小时
C. D.
9. 如图,将弧沿弦翻折恰好过圆心点,点为弧的中点,的半径为3,则图中阴影部分的面积为( )
A B. C. D.
10. 我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”,如图,这个三角形给出了的展开式的系数规律(按的次数由大到小的顺序):
请依据上述规律判断:若今天是星期三,则经过天后是( )
A. 星期四 B. 星期五 C. 星期六 D. 星期天
二、填空题(本题共6小题,每小题3分,共18分)
11. 若某商品每件涨价10元记作+10元,那么该商品每件降价8元记作 _____元.
12. 反比例函数的图像与点的位置如图,写出一个与图相符的反比例函数解析式为_____.
13. 计算的结果是__________.
14. 某商场从安全和便利的角度出发,为提升顾客的购物体验,准备将自动扶梯由原来的阶梯式改造成斜坡式,如图,已知商场的层高为,坡角为,改造后的斜坡式自动扶梯的坡角,请你计算改造后的自动扶梯增加的占地长度_____(结果精确到,参考数据:,,)
15. 如图,点为矩形边的中点,点在边上,且,将沿翻折得到,延长交边于点,且,则___________.
16. 对于函数,有以下结论:
①函数图像为轴对称图形,对称轴是轴;
②当时,函数有最小值;
③若函数图像与轴有3个交点,;
④若关于方程有4个实数根,则;
⑤若图像上有两点,当时,,则.
其中正确的结论是___________.(填写序号)
三、解答题(共8题,共72分)
17. 求不等式组的整数解.
18. 如图,点,分别在的边,上,,连接,.请从以下三个条件:①;②;③中,选择一个合适的作为已知条件,使为菱形.
(1)你添加的条件是______(填序号);
(2)添加了条件后,请证明菱形.
19. 某中学全校学生参加了“交通法规”知识竞赛,为了解全校学生竞赛成绩的情况,随机抽取了一部分学生的成绩,分成四组:组()、组()、C组()、组(),并绘制出如图不完整的统计图.
(1)被抽取的学生一共有___________人;并把条形统计图补完整;所抽取学生成绩的中位数落在___________组内;
(2)若该学校有1200名学生,估计这次竞赛成绩在D组的学生有多少人?
(3)根据以上调查数据,简要谈谈你关于该校学生“交通法规”掌握情况的看法,并结合自己的实际,对同学们提一条遵守“交通法规”的建议(字数不超过30个字).
20. 如图, 中,,是角平分线,以为圆心,为半径的交.
(1)求证:是的切线;
(2)若,求的值.
21. 如图是由小正方形构成的网格,每个小正方形的顶点叫做格点.的顶点在格点上,仅用无刻度直尺在给定网格中画图,按步骤完成下列问题,每个作图任务不超过三条线:
(1)在图1中,先将线段绕点逆时针旋转得到线段;再在边上找一点,使.
(2)在图2中,先作的角平分线;再在边上找点使得.
22. 如图,用一段长为的篱笆围成一个一边靠墙(无需篱笆)的矩形菜园,并且中间用篱笆隔开,,墙长,设,矩形面积为.
(1)关于的函数解析式为___________(写化简后结果),的取值范围是_________;
(2)求菜园面积最大值,并求此时的长;
(3)在(2)的前提下,若将矩形和矩形分别种植甲、乙两种农作物.甲农作物的年收入(单位:元)与种植面积(单位:)的函数关系式为,乙农作物的年收入(单位:元)与种植面积(单位:)的函数关系式为,两种农作物年收入之和不小于8918元,并且乙农作物的种植面积不小于甲农作物的种植面积的两倍.设,求的取值范围.
23. (1)如图1,在正方形中,点是边上一点,且点不与点、重合,点是的延长线上一点,且.
①求证:;
②如图2,连接,交于点,交于点,连接.若,求的长.
(2)如图3,在正方形中,点在边上,且,点为边上的动点,连接,过点作,交射线于点,则___________.(用含有的式子表示)
24. 如图1,在平面直角坐标系中,抛物线与轴交于A、两点,与轴交于点,顶点坐标为,点是第一象限抛物线上的一动点.
(1)求抛物线的函数表达式;
(2)如图2,连接,,,线段与相交于点,设,求出的最大值;
(3)如图3,点为第四象限抛物线上的另一动点,连接交轴于点,线段与轴的交点记为G,,试探究直线是否过某一定点.若是,请求出该定点的坐标;若不是,请说明理由.
答案
一、选择题(本题共10小题,每小题3分,共30分)
【1 】D
【2 】D
【3 】A
【4 】C
【5 】C
【6 】B
【7 】C
【8 】C
【9 】C
【10 】A
二、填空题(本题共6小题,每小题3分,共18分)
【11 】-8
【12 】(答案不唯一)
【13 】
【14 】m##10.3米
【15 】
【16 】①③④⑤
三、解答题(共8题,共72分)
【17 】,,,.
【18 】(1)① (2)见解析
【19 】(1)90,C,补全图形见解答
(2)320名 (3)答案不唯一,合理即可
【20 】(1)略 (2)
【21 】(1)略 (2)略
【22 】(1),
(2)菜园面积的最大值为,此时的长为
(3)
【23 】(1)①略;②;(2)
【24 】(1)
(2)
(3)直线过定点.
一、选择题(本题共10小题,每小题3分,共30分)
1. 现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字是轴对称图形的是( )
A. B. C. D.
2. 在下列事件中,必然事件是( )
A. 掷一次骰子,向上一面的点数是3
B. 篮球队员在罚球线上投篮一次,未投中
C. 经过有交通信号灯的路口,遇到红灯
D. 任意画一个三角形,其内角和180°
3. 如图是由4个相同的小正方体组成的几何体,它的主视图是( )
A. B.
C. D.
4. 国家统计局2024年4月16日发布数据,今年第一季度国内生产总值接近亿元,同比增长,国家高质量发展取得新成效.将数据用科学记数法表示是( )
A. B. C. D.
5. 下列运算正确的是( )
A. B.
C. D.
6. 如图,直线,的直角顶点在直线上,若,,则的度数为( )
A. B. C. D.
7. 第一个盒子有2个白球,1个黄球,第二个盒子有1个白球,1个黄球,这些球除颜色外无其他差别.分别从每个盒子中随机取出1个球,那么取出的2个球中1个白球1个黄球的概率是( )
A. B. C. D.
8. 两人分别骑自行车、摩托车沿相同路线,先后由地抵达地,、两地相距.请结合图象判断下列结论,其中错误的是( )
A. 摩托车的平均速度是 B. 自行车比摩托车早出发2小时
C. D.
9. 如图,将弧沿弦翻折恰好过圆心点,点为弧的中点,的半径为3,则图中阴影部分的面积为( )
A B. C. D.
10. 我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”,如图,这个三角形给出了的展开式的系数规律(按的次数由大到小的顺序):
请依据上述规律判断:若今天是星期三,则经过天后是( )
A. 星期四 B. 星期五 C. 星期六 D. 星期天
二、填空题(本题共6小题,每小题3分,共18分)
11. 若某商品每件涨价10元记作+10元,那么该商品每件降价8元记作 _____元.
12. 反比例函数的图像与点的位置如图,写出一个与图相符的反比例函数解析式为_____.
13. 计算的结果是__________.
14. 某商场从安全和便利的角度出发,为提升顾客的购物体验,准备将自动扶梯由原来的阶梯式改造成斜坡式,如图,已知商场的层高为,坡角为,改造后的斜坡式自动扶梯的坡角,请你计算改造后的自动扶梯增加的占地长度_____(结果精确到,参考数据:,,)
15. 如图,点为矩形边的中点,点在边上,且,将沿翻折得到,延长交边于点,且,则___________.
16. 对于函数,有以下结论:
①函数图像为轴对称图形,对称轴是轴;
②当时,函数有最小值;
③若函数图像与轴有3个交点,;
④若关于方程有4个实数根,则;
⑤若图像上有两点,当时,,则.
其中正确的结论是___________.(填写序号)
三、解答题(共8题,共72分)
17. 求不等式组的整数解.
18. 如图,点,分别在的边,上,,连接,.请从以下三个条件:①;②;③中,选择一个合适的作为已知条件,使为菱形.
(1)你添加的条件是______(填序号);
(2)添加了条件后,请证明菱形.
19. 某中学全校学生参加了“交通法规”知识竞赛,为了解全校学生竞赛成绩的情况,随机抽取了一部分学生的成绩,分成四组:组()、组()、C组()、组(),并绘制出如图不完整的统计图.
(1)被抽取的学生一共有___________人;并把条形统计图补完整;所抽取学生成绩的中位数落在___________组内;
(2)若该学校有1200名学生,估计这次竞赛成绩在D组的学生有多少人?
(3)根据以上调查数据,简要谈谈你关于该校学生“交通法规”掌握情况的看法,并结合自己的实际,对同学们提一条遵守“交通法规”的建议(字数不超过30个字).
20. 如图, 中,,是角平分线,以为圆心,为半径的交.
(1)求证:是的切线;
(2)若,求的值.
21. 如图是由小正方形构成的网格,每个小正方形的顶点叫做格点.的顶点在格点上,仅用无刻度直尺在给定网格中画图,按步骤完成下列问题,每个作图任务不超过三条线:
(1)在图1中,先将线段绕点逆时针旋转得到线段;再在边上找一点,使.
(2)在图2中,先作的角平分线;再在边上找点使得.
22. 如图,用一段长为的篱笆围成一个一边靠墙(无需篱笆)的矩形菜园,并且中间用篱笆隔开,,墙长,设,矩形面积为.
(1)关于的函数解析式为___________(写化简后结果),的取值范围是_________;
(2)求菜园面积最大值,并求此时的长;
(3)在(2)的前提下,若将矩形和矩形分别种植甲、乙两种农作物.甲农作物的年收入(单位:元)与种植面积(单位:)的函数关系式为,乙农作物的年收入(单位:元)与种植面积(单位:)的函数关系式为,两种农作物年收入之和不小于8918元,并且乙农作物的种植面积不小于甲农作物的种植面积的两倍.设,求的取值范围.
23. (1)如图1,在正方形中,点是边上一点,且点不与点、重合,点是的延长线上一点,且.
①求证:;
②如图2,连接,交于点,交于点,连接.若,求的长.
(2)如图3,在正方形中,点在边上,且,点为边上的动点,连接,过点作,交射线于点,则___________.(用含有的式子表示)
24. 如图1,在平面直角坐标系中,抛物线与轴交于A、两点,与轴交于点,顶点坐标为,点是第一象限抛物线上的一动点.
(1)求抛物线的函数表达式;
(2)如图2,连接,,,线段与相交于点,设,求出的最大值;
(3)如图3,点为第四象限抛物线上的另一动点,连接交轴于点,线段与轴的交点记为G,,试探究直线是否过某一定点.若是,请求出该定点的坐标;若不是,请说明理由.
答案
一、选择题(本题共10小题,每小题3分,共30分)
【1 】D
【2 】D
【3 】A
【4 】C
【5 】C
【6 】B
【7 】C
【8 】C
【9 】C
【10 】A
二、填空题(本题共6小题,每小题3分,共18分)
【11 】-8
【12 】(答案不唯一)
【13 】
【14 】m##10.3米
【15 】
【16 】①③④⑤
三、解答题(共8题,共72分)
【17 】,,,.
【18 】(1)① (2)见解析
【19 】(1)90,C,补全图形见解答
(2)320名 (3)答案不唯一,合理即可
【20 】(1)略 (2)
【21 】(1)略 (2)略
【22 】(1),
(2)菜园面积的最大值为,此时的长为
(3)
【23 】(1)①略;②;(2)
【24 】(1)
(2)
(3)直线过定点.
同课章节目录
