21.2.2 公式法 课件(共31张PPT) 人教版数学九年级上册
文档属性
| 名称 | 21.2.2 公式法 课件(共31张PPT) 人教版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 05:47:27 | ||
图片预览










文档简介
(共31张PPT)
21.2 解一元二次方程
第二十一章 一元二次方程
21.2.2 公式法
复习引入
解:方程整理得
配方得
开平方得
解得
1. 如何用配方法解方程 2x2 + 4x - 1 = 0
想一想 任何一个一元二次方程都可以写成一般形式
ax2 + bx + c = 0 (a ≠ 0).
能否也用配方法得出它的解呢?
合作探究
用配方法解一般形式一元二次方程 ax2 + bx + c = 0 (a ≠ 0).
方程两边都除以 a,得
解:移项,得
配方,得
即
问题:对于方程①接下来能用直接开平方解吗?
求根公式的推导
∵ a≠0,∴ 4a2 > 0.
而 b2-4ac 的符号有以下三种情况:
(1)b2-4ac >0,
这时 >0,由①得
则方程有两个不相等的实数根
(2)b2 - 4ac = 0,
这时 = 0,由①可知,方程有两个相等的实数根 x1 = x2 = - .
(3)b2 - 4ac <0,
这时 <0,由①可知 <0,而 x 取任何实数都不能使 <0,因此方程无实数根.
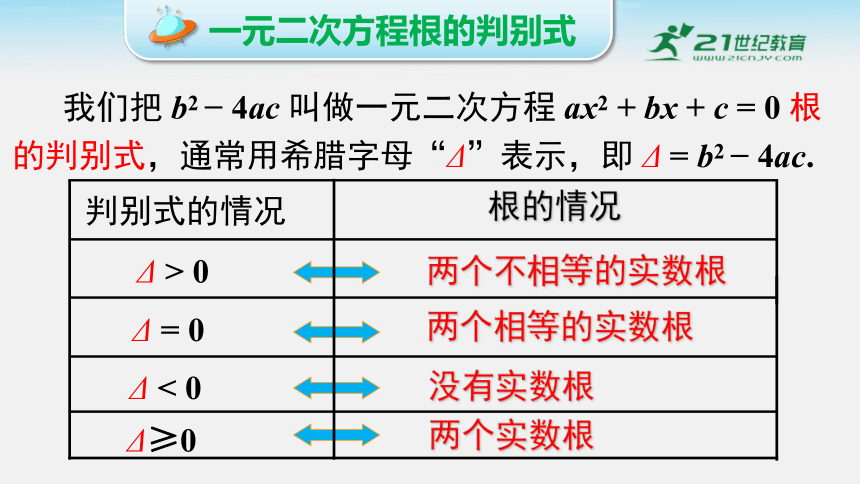
两个不相等的实数根
两个相等的实数根
没有实数根
两个实数根
判别式的情况
根的情况
我们把 b2 4ac 叫做一元二次方程 ax2 + bx + c = 0 根的判别式,通常用希腊字母“Δ”表示,即 Δ = b2 4ac.
Δ > 0
Δ = 0
Δ < 0
Δ≥0
一元二次方程根的判别式
按要求完成下列表格:
练一练
的值
0
4
根的 情况
有两个相等的实数根
没有实数根
有两个不相等的实数根
Δ
例1 已知一元二次方程 x2 + x = 1,下列判断正确的是( )
A. 该方程有两个相等的实数根
B. 该方程有两个不相等的实数根
C. 该方程无实数根
D. 该方程根的情况不确定
解析:原方程即 x2 + x 1 = 0,a = 1,b = 1,c = 1,
∵ Δ = b2 4ac = 12 4×1×( 1) = 5>0,
∴ 该方程有两个不等的实数根,故选 B.
B
典例精析
例2 不解方程,判断下列方程的根的情况:
(1)3x2 + 4x 3 = 0; (2)4x2 = 12x 9;
解:(1)a = 3,b = 4,c = 3,
∴ Δ = b2 4ac = 42 4×3×( 3) = 52>0.
∴ 方程有两个不相等的实数根.
(2)方程化为 4x2 12x + 9 = 0,a = 4,b = 12,c = 9,
∴ Δ = b2 4ac = ( 12)2 4×4×9 = 0.
∴ 方程有两个相等的实数根.
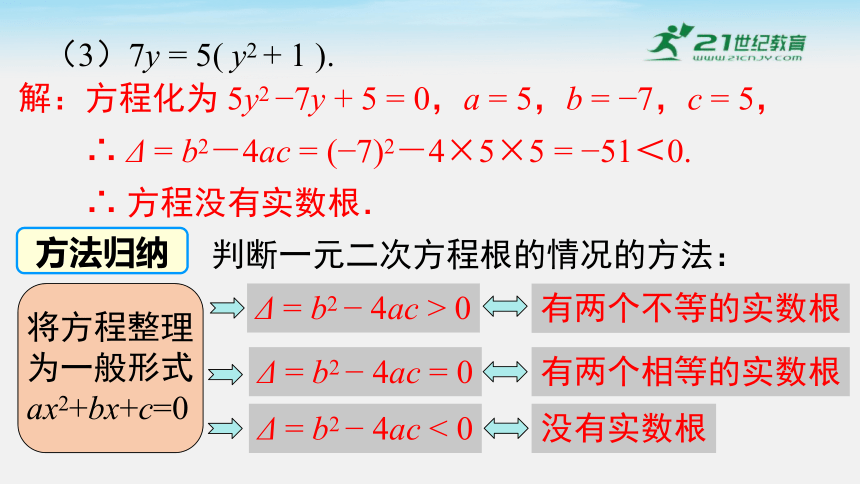
(3)7y = 5( y2 + 1 ).
解:方程化为 5y2 7y + 5 = 0,a = 5,b = 7,c = 5,
∴ Δ = b2-4ac = ( 7)2-4×5×5 = 51<0.
∴ 方程没有实数根.
方法归纳
判断一元二次方程根的情况的方法:
将方程整理为一般形式
ax2+bx+c=0
Δ = b2 4ac > 0
Δ = b2 4ac = 0
Δ = b2 4ac < 0
有两个不等的实数根
有两个相等的实数根
没有实数根
例3 若关于 x 的一元二次方程 x2 + 8x + q = 0 有两个不等的实数根,则 q 的取值范围是 ( )
A. q≤4 B. q≥4
C. q<16 D. q>16
C
解析:方程有两个不等的实数根,根据根的判别式,则 Δ = b2 4ac>0,即 82 4q>0. 解得 q<16,故选 C.
典例精析
【变式题】二次项系数含字母
若关于 x 的一元二次方程 kx2 2x 1 = 0 有两个不等的实数根,则 k 的取值范围是 ( )
A. k > 1 B. k > 1 且 k≠0
C. k < 1 D. k < 1 且 k≠0
B
(-2)2 + 4k > 0
当一元二次方程二次项系数是字母时,一定要注意二次项系数不为 0,再根据“Δ”求字母的取值范围.
归纳
方程有两个不等的实数根
分析:
二次项系数不为 0
k≠0
k > 1 且 k≠0
【变式题】删除限制条件“二次”
若关于 x 的方程 kx2 2x 1 = 0 有实数根,则 k 的取值范围是( )
A. k≥ 1 B. k≥ 1且 k≠0
C. k < 1 D. k < 1 且 k≠0
分析:
分类讨论
k = 0
k≠0
原方程变形为 2x 1 = 0,有实数根
Δ = 4 + 4k≥0
k≥ 1
A
由上可知,当 Δ≥0 时,方程 ax2 + bx + c = 0 (a≠0)的实数根可写为 的形式,这个式子叫做一元二次方程 ax2 + bx + c = 0 的求根公式.
注意:用公式法解一元二次方程时,首先要将方程化为一般式,然后当 Δ = b2 - 4ac≥0 时,才可以用求根公式.
用求根公式解一元二次方程的方法叫做公式法.
用公式法解方程
视频:求根公式的趣味记忆
点击视频开始播放←
例4 用公式法解下列方程:
典例精析
(1) x2 4x 7 = 0;
方程有两个不等的实数根
解:a = 1,b = 4,c = 7.
Δ = b2-4ac = ( 4)2-4×1×( 7) = 44>0.
即
方程有两个相等的实数根
x1 = x2
(2) 2x2 x + 1 = 0;
解:a = 2,b = ,c = 1.
Δ = b2-4ac = ( )2-4×2×1 = 0.
(3) 5x2-3x = x + 1;
方程有两个不等的实数根
即
a = 5,b = -4,c = -1.
Δ = b2-4ac = (-4)2-4×5×(-1) = 36>0.
解:方程化为 5x2-4x-1 = 0.
(4) x2 + 17 = 8x.
方程没有实数根.
a = 1,b = 8,c = 17.
Δ = b2 4ac = ( 8)2 4×1×17 = 4<0.
解:方程化为 x2-8x + 17 = 0.
要点归纳
公式法解方程的步骤
1. 变形:化已知方程为一般形式;
2. 确定系数:用 a,b,c 写出各项系数;
3. 计算:b2 4ac 的值;
4. 判断:若 Δ = b2 4ac≥0,则利用求根公式求出;
若 b2 4ac<0,则方程没有实数根.
1. 不解方程,判断下列方程的根的情况:
(1)2x2 + 3x 4 = 0; (2)x2 x + = 0;
解:(1)a = 2,b = 3,c = 4,
∴ Δ = b2 4ac = 32 4×2×( 4) = 41>0.
∴ 方程有两个不等的实数根.
(2)a = 1,b = 1,c = ,
∴ Δ = b2 4ac = ( 1)2 4×1× = 0.
∴ 方程有两个相等的实数根.
解:x2 x + 1 = 0,a = 1,b = 1,c = 1,
∴ Δ = b2 4ac = ( 1)2 4×1×1 = 3 < 0.
∴ 方程无实数根.
(3) x2 x + 1 = 0.
2. 解方程:x2 + 7x – 18 = 0.
解:a = 1,b = 7,c = 18,
∴ Δ = b2 - 4ac = 72 – 4×1×( 18 ) = 121 > 0,
即 x1 = 9, x2 = 2 .
3. 解方程:(x - 2) (1 - 3x) = 6.
解:去括号,得 x - 2 - 3x2 + 6x = 6,
化为一般式,得 3x2 - 7x + 8 = 0,
a = 3,b = -7,c = 8,
∴ Δ = b2 - 4ac = (-7 )2 – 4×3×8 = 49–96
= - 47 < 0,
∴ 原方程没有实数根.
4. 解方程:2x2 - x + 3 = 0.
解: a = 2,b = ,c = 3 .
∴ Δ = b2 - 4ac = 27 - 4×2×3 = 3 > 0 ,
5. (1) 关于 x 的一元二次方程 有两个实根,则 m 的取值范围是 .
(2) 若关于 x 的一元二次方程 (m 1)x2 2mx + m = 2 有实数根.求 m 的取值范围.
解:化为一般式,得 (m 1)x2 2mx + m 2 = 0.
Δ = 4m2 4(m 1)(m 2)≥0,且 m 1≠0.
解得
且 m≠1.
6. 不解方程,判断关于 x 的方程
的根的情况.
解:
∴ 原方程有两个实数根.
Δ =( k )2 4×1×k2 = 4k2.
∵ k2≥0,
∴ 4k2≥0,
即 Δ≥0.
能力提升:在等腰△ABC 中,三边长分别为 a,b,c,其中 a = 5,若关于 x 的方程 x2 + (b + 2)x + 6 - b = 0 有两个相等的实数根,求△ABC 的周长.
解:∵关于 x 的方程 x2 + (b + 2)x + 6 b = 0 有两个相等的实数根,
∴ Δ = (b + 2)2 4(6 b) = b2 + 8b 20 = 0.
解得 b1= 10(舍去),b2 = 2.
由三角形的三边关系,得 c = 5,
∴△ABC 的三边长为 5,2,5,其周长为 5 + 2 + 5 = 12.
公式法
求根公式
步骤
一化(一般形式);
二定(系数值);
三求(求 b2 - 4ac 的值);
四判(方程根的情况);
五代(代求根公式计算)
务必将方程
化为一般形式
判断一元二次方程 ax2 + bx + c = 0 (a ≠ 0)根情况的方法:
Δ =b2 4ac > 0
Δ =b2 4ac = 0
Δ =b2 4ac< 0
有两个不等的实数根
有两个相等的实数根
没有实数根
21.2 解一元二次方程
第二十一章 一元二次方程
21.2.2 公式法
复习引入
解:方程整理得
配方得
开平方得
解得
1. 如何用配方法解方程 2x2 + 4x - 1 = 0
想一想 任何一个一元二次方程都可以写成一般形式
ax2 + bx + c = 0 (a ≠ 0).
能否也用配方法得出它的解呢?
合作探究
用配方法解一般形式一元二次方程 ax2 + bx + c = 0 (a ≠ 0).
方程两边都除以 a,得
解:移项,得
配方,得
即
问题:对于方程①接下来能用直接开平方解吗?
求根公式的推导
∵ a≠0,∴ 4a2 > 0.
而 b2-4ac 的符号有以下三种情况:
(1)b2-4ac >0,
这时 >0,由①得
则方程有两个不相等的实数根
(2)b2 - 4ac = 0,
这时 = 0,由①可知,方程有两个相等的实数根 x1 = x2 = - .
(3)b2 - 4ac <0,
这时 <0,由①可知 <0,而 x 取任何实数都不能使 <0,因此方程无实数根.
两个不相等的实数根
两个相等的实数根
没有实数根
两个实数根
判别式的情况
根的情况
我们把 b2 4ac 叫做一元二次方程 ax2 + bx + c = 0 根的判别式,通常用希腊字母“Δ”表示,即 Δ = b2 4ac.
Δ > 0
Δ = 0
Δ < 0
Δ≥0
一元二次方程根的判别式
按要求完成下列表格:
练一练
的值
0
4
根的 情况
有两个相等的实数根
没有实数根
有两个不相等的实数根
Δ
例1 已知一元二次方程 x2 + x = 1,下列判断正确的是( )
A. 该方程有两个相等的实数根
B. 该方程有两个不相等的实数根
C. 该方程无实数根
D. 该方程根的情况不确定
解析:原方程即 x2 + x 1 = 0,a = 1,b = 1,c = 1,
∵ Δ = b2 4ac = 12 4×1×( 1) = 5>0,
∴ 该方程有两个不等的实数根,故选 B.
B
典例精析
例2 不解方程,判断下列方程的根的情况:
(1)3x2 + 4x 3 = 0; (2)4x2 = 12x 9;
解:(1)a = 3,b = 4,c = 3,
∴ Δ = b2 4ac = 42 4×3×( 3) = 52>0.
∴ 方程有两个不相等的实数根.
(2)方程化为 4x2 12x + 9 = 0,a = 4,b = 12,c = 9,
∴ Δ = b2 4ac = ( 12)2 4×4×9 = 0.
∴ 方程有两个相等的实数根.
(3)7y = 5( y2 + 1 ).
解:方程化为 5y2 7y + 5 = 0,a = 5,b = 7,c = 5,
∴ Δ = b2-4ac = ( 7)2-4×5×5 = 51<0.
∴ 方程没有实数根.
方法归纳
判断一元二次方程根的情况的方法:
将方程整理为一般形式
ax2+bx+c=0
Δ = b2 4ac > 0
Δ = b2 4ac = 0
Δ = b2 4ac < 0
有两个不等的实数根
有两个相等的实数根
没有实数根
例3 若关于 x 的一元二次方程 x2 + 8x + q = 0 有两个不等的实数根,则 q 的取值范围是 ( )
A. q≤4 B. q≥4
C. q<16 D. q>16
C
解析:方程有两个不等的实数根,根据根的判别式,则 Δ = b2 4ac>0,即 82 4q>0. 解得 q<16,故选 C.
典例精析
【变式题】二次项系数含字母
若关于 x 的一元二次方程 kx2 2x 1 = 0 有两个不等的实数根,则 k 的取值范围是 ( )
A. k > 1 B. k > 1 且 k≠0
C. k < 1 D. k < 1 且 k≠0
B
(-2)2 + 4k > 0
当一元二次方程二次项系数是字母时,一定要注意二次项系数不为 0,再根据“Δ”求字母的取值范围.
归纳
方程有两个不等的实数根
分析:
二次项系数不为 0
k≠0
k > 1 且 k≠0
【变式题】删除限制条件“二次”
若关于 x 的方程 kx2 2x 1 = 0 有实数根,则 k 的取值范围是( )
A. k≥ 1 B. k≥ 1且 k≠0
C. k < 1 D. k < 1 且 k≠0
分析:
分类讨论
k = 0
k≠0
原方程变形为 2x 1 = 0,有实数根
Δ = 4 + 4k≥0
k≥ 1
A
由上可知,当 Δ≥0 时,方程 ax2 + bx + c = 0 (a≠0)的实数根可写为 的形式,这个式子叫做一元二次方程 ax2 + bx + c = 0 的求根公式.
注意:用公式法解一元二次方程时,首先要将方程化为一般式,然后当 Δ = b2 - 4ac≥0 时,才可以用求根公式.
用求根公式解一元二次方程的方法叫做公式法.
用公式法解方程
视频:求根公式的趣味记忆
点击视频开始播放←
例4 用公式法解下列方程:
典例精析
(1) x2 4x 7 = 0;
方程有两个不等的实数根
解:a = 1,b = 4,c = 7.
Δ = b2-4ac = ( 4)2-4×1×( 7) = 44>0.
即
方程有两个相等的实数根
x1 = x2
(2) 2x2 x + 1 = 0;
解:a = 2,b = ,c = 1.
Δ = b2-4ac = ( )2-4×2×1 = 0.
(3) 5x2-3x = x + 1;
方程有两个不等的实数根
即
a = 5,b = -4,c = -1.
Δ = b2-4ac = (-4)2-4×5×(-1) = 36>0.
解:方程化为 5x2-4x-1 = 0.
(4) x2 + 17 = 8x.
方程没有实数根.
a = 1,b = 8,c = 17.
Δ = b2 4ac = ( 8)2 4×1×17 = 4<0.
解:方程化为 x2-8x + 17 = 0.
要点归纳
公式法解方程的步骤
1. 变形:化已知方程为一般形式;
2. 确定系数:用 a,b,c 写出各项系数;
3. 计算:b2 4ac 的值;
4. 判断:若 Δ = b2 4ac≥0,则利用求根公式求出;
若 b2 4ac<0,则方程没有实数根.
1. 不解方程,判断下列方程的根的情况:
(1)2x2 + 3x 4 = 0; (2)x2 x + = 0;
解:(1)a = 2,b = 3,c = 4,
∴ Δ = b2 4ac = 32 4×2×( 4) = 41>0.
∴ 方程有两个不等的实数根.
(2)a = 1,b = 1,c = ,
∴ Δ = b2 4ac = ( 1)2 4×1× = 0.
∴ 方程有两个相等的实数根.
解:x2 x + 1 = 0,a = 1,b = 1,c = 1,
∴ Δ = b2 4ac = ( 1)2 4×1×1 = 3 < 0.
∴ 方程无实数根.
(3) x2 x + 1 = 0.
2. 解方程:x2 + 7x – 18 = 0.
解:a = 1,b = 7,c = 18,
∴ Δ = b2 - 4ac = 72 – 4×1×( 18 ) = 121 > 0,
即 x1 = 9, x2 = 2 .
3. 解方程:(x - 2) (1 - 3x) = 6.
解:去括号,得 x - 2 - 3x2 + 6x = 6,
化为一般式,得 3x2 - 7x + 8 = 0,
a = 3,b = -7,c = 8,
∴ Δ = b2 - 4ac = (-7 )2 – 4×3×8 = 49–96
= - 47 < 0,
∴ 原方程没有实数根.
4. 解方程:2x2 - x + 3 = 0.
解: a = 2,b = ,c = 3 .
∴ Δ = b2 - 4ac = 27 - 4×2×3 = 3 > 0 ,
5. (1) 关于 x 的一元二次方程 有两个实根,则 m 的取值范围是 .
(2) 若关于 x 的一元二次方程 (m 1)x2 2mx + m = 2 有实数根.求 m 的取值范围.
解:化为一般式,得 (m 1)x2 2mx + m 2 = 0.
Δ = 4m2 4(m 1)(m 2)≥0,且 m 1≠0.
解得
且 m≠1.
6. 不解方程,判断关于 x 的方程
的根的情况.
解:
∴ 原方程有两个实数根.
Δ =( k )2 4×1×k2 = 4k2.
∵ k2≥0,
∴ 4k2≥0,
即 Δ≥0.
能力提升:在等腰△ABC 中,三边长分别为 a,b,c,其中 a = 5,若关于 x 的方程 x2 + (b + 2)x + 6 - b = 0 有两个相等的实数根,求△ABC 的周长.
解:∵关于 x 的方程 x2 + (b + 2)x + 6 b = 0 有两个相等的实数根,
∴ Δ = (b + 2)2 4(6 b) = b2 + 8b 20 = 0.
解得 b1= 10(舍去),b2 = 2.
由三角形的三边关系,得 c = 5,
∴△ABC 的三边长为 5,2,5,其周长为 5 + 2 + 5 = 12.
公式法
求根公式
步骤
一化(一般形式);
二定(系数值);
三求(求 b2 - 4ac 的值);
四判(方程根的情况);
五代(代求根公式计算)
务必将方程
化为一般形式
判断一元二次方程 ax2 + bx + c = 0 (a ≠ 0)根情况的方法:
Δ =b2 4ac > 0
Δ =b2 4ac = 0
Δ =b2 4ac< 0
有两个不等的实数根
有两个相等的实数根
没有实数根
同课章节目录
