安徽省合肥市百花中学等四校联考2024-2025学年高一下学期7月期末考试数学试卷(含解析)
文档属性
| 名称 | 安徽省合肥市百花中学等四校联考2024-2025学年高一下学期7月期末考试数学试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 813.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 22:46:38 | ||
图片预览




文档简介
安徽省合肥市百花中学等四校联考2024-2025学年高一下学期期末考试数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列各式的运算结果为纯虚数的是( )
A. B. C. D.
2.已知篮球运动员甲、乙的罚球命中率分别为0.9,0.8,且两人罚球是否命中相互独立.若甲、乙各罚球一次,则恰有一人命中的概率为( )
A.0.26 B.0.28 C.0.72 D.0.98
3.在中,角的对边分别为,若,则的形状为( )
A.直角三角形 B.等腰三角形 C.等腰直角三角形 D.等边三角形
4.在正方体中,为棱的中点,则异面直线与所成角的正切值为
A. B. C. D.
5.从长度分别为3,4,5,6的4条线段中任取3条,能构成钝角三角形的概率为( )
A. B. C. D.
6.已知分别为内角的对边,的面积,则( )
A. B. C. D.
7.甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为,侧面积分别为和,体积分别为和.若,则( )
A. B. C. D.
二、多选题
8.已知表示两条不同直线,a表示平面,则下列选项正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
9.有一组样本数据,其中是最小值,是最大值,则( )
A.的平均数等于的平均数
B.的中位数等于的中位数
C.的标准差不小于的标准差
D.的极差不大于的极差
10.已知向量,,则( )
A. B.
C. D.在方向上的投影向量的坐标为
11.如图,正方体的棱长为2,是棱的中点,是侧面上的动点,且满足,则下列结论中正确的是( )
A.平面截正方体所得截面面积为
B.点的轨迹长度为
C.存在点,使得
D.直线与平面所成角的正弦值的最大值为
三、填空题
12.已知平面内有、、、四点,其中,,三点共线,且,则 .
13.已知三棱锥的所有顶点都在球O的球面上,SC是球O的直径若平面平面SCB,,,三棱锥的体积为9,则球O的表面积为 .
14.的内角,,的对边分别为,,,已知,,,则的最大值为 .
四、解答题
15.已知复数满足
(1)求复数
(2)若复数是关于的方程的一个根,求,的值
16.在中,内角A,B,C的对边a,b,c,且,已知,,,求:
(1)a和c的值;
(2)的值.
17.某研究机构为了了解各年龄层对高考改革方案的关注程度,随机选取了200名年龄在内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为,,,,,).
(1)求选取的市民年龄在内的人数;
(2)利用频率分布直方图,估计200名市民的年龄的平均数和第80百分位数;
(3)若从第3,4组用分层抽样的方法选取5名市民进行座谈,再从中选取2人在座谈会中作重点发言,求作重点发言的市民中至少有一人的年龄在内的概率.
18.如图,在梯形中,,,,为线段的中点,记,.
(1)用,表示向量;
(2)求的值;
(3)求与夹角的余弦值.
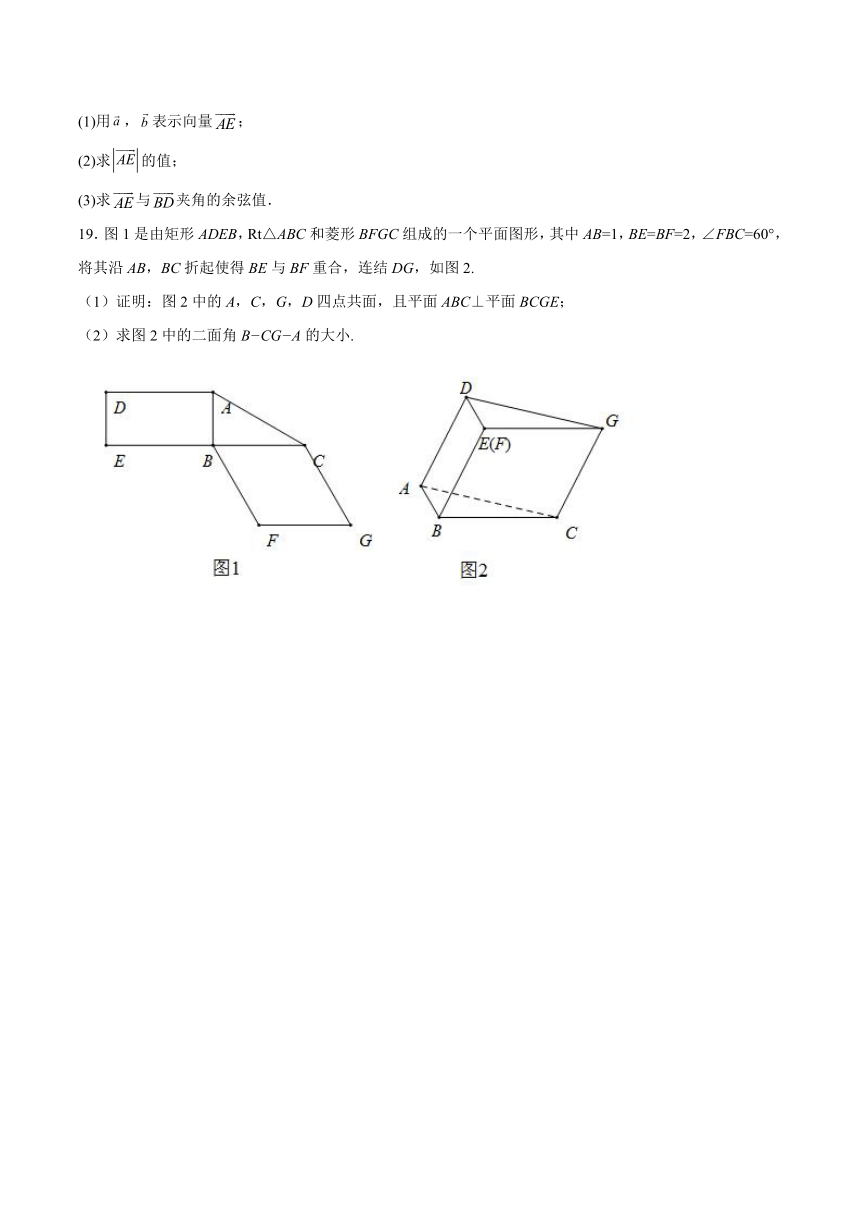
19.图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.
(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的二面角B CG A的大小.
安徽省合肥市百花中学等四校联考2024-2025学年高一下学期期末考试数学试题参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B C C C C BD BD ACD
题号 11
答案 AC
1.B
详解:,,,,
通过比较可以知道,只有为纯虚数,故选B.
2.A
【详解】设“篮球运动员甲、乙的罚球命中”分别为事件A,B,“恰有一人命中”为事件C,
则
.
故选:A.
3.B
【详解】因,由正弦定理,,即,
因,则,故, ,即,故是等腰三角形.
故选:B.
4.C
【详解】在正方体中,,所以异面直线与所成角为,
设正方体边长为,则由为棱的中点,可得,所以,
则.故选C.
5.C
【详解】从4条线段中取3条的组合数为:,具体为:①3,4,5;②3,4,6;③3,5,6;④4,5,6.
设三角形边长为a,b,c,c为最大边,则:
钝角三角形的满足条件为:.
组合①:
组合②:
组合③:
组合④:
综上,满足钝角三角形的组合数为2,概率.
故选:C.
6.C
【详解】由余弦定理得,
又三角形面积公式得,
故,
又,故,即,
又,故.
故选:C
7.C
【详解】设甲、乙两个圆锥的母线长均为,底面半径分别为,
则,所以①,
因为侧面展开图的圆心角之和为,
所以,即②,
由①②解得,
所以甲圆锥的高,乙圆锥的高,
所以.
故选:C.
8.BD
【详解】对于A,若,,则或者异面,或者相交,故A错误,
对于B,若,,则,故B正确,
对于C,若,,则或者,故C错误,
对于D,若,,则,D正确,
故选:BD
9.BD
【详解】对于A,不妨取为,其平均数为,
为,其平均数为1,
此时的平均数不等于的平均数,A错误;
对于B,不妨设,则中位数为,
的中位数也为,故B正确;
对于C,取为,平均数为,
其标准差为,
即为,平均数为,
则其标准差为,
因为,所以,
此时的标准差小于的标准差,故C错误;
对于D,不妨设,
则,当且仅当时等号成立,
即的极差不大于的极差,故D正确.
故选:BD.
10.ACD
【详解】选项A:已知向量,,
所以,,故A对;
选项B:因为,而,故B错;
选项C:因为,,故C对;
选项D:根据投影向量公式:,故D对.
故选:ACD.
11.AC
【详解】
已知正方体的棱长为2,是棱的中点,是侧面上的动点,
且满足,取的中点G,连接、,
则等腰梯形(,且)为其截面,
面积为,故A对;
取中点M,中点N,连接,,,
由题可得,,且平面,
所以平面,平面,
又与是平面内的两条相交直线,
所以平面平面,所以点F的运动轨迹为线段,长度为,故B错;
取中点F,因为为等腰三角形,所以,
又因为,所以,故C对.
因为平面,所以为与平面所成的线面角,
所以,
因为,且时最小,满足题设正弦值最大,
所以,,故D错.
故选:AC.
12.1
【详解】因为,,三点共线,所以存在使得
由
所以
即
故答案为:1
13.36π
【详解】三棱锥S ABC的所有顶点都在球O的球面上,SC是球O的直径,
若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S ABC的体积为9,
可知三角形SBC与三角形SAC都是等腰直角三角形,设球的半径为r,
可得 ,解得r=3.
球O的表面积为: .
14.
【详解】由题得,
因为,
所以,
所以,
因为,所以.
由正弦定理得.
所以
,
所以的最大值为,此时.
故答案为:
15.(1)
(2)
【详解】(1)因为,
所以.
(2)因为复数是关于的方程的一个根,
所以,
所以,解得.
16.(1);(2)
【详解】
(1)由得,,又,所以ac=6.
由余弦定理,得.
又b=3,所以.
解,得a=2,c=3或a=3,c=2.
因为a>c,∴ a=3,c=2.
(2)在中,
由正弦定理,得,又因为,所以C为锐角,因此.
于是=.
考点:1.解三角形;2.三角恒等变换.
17.(1)20
(2)平均数32.25; 第80百分位数37.5
(3)
【详解】(1)(1)由题意可知,年龄在内的频率为,
故年龄在内的市民人数为.
(2)(2) 平均数为
32.25;
前三组的频率和为,
第四组的频率为,所以第80百分位数在第四组,
第80百分位数为.
(3)(3)易知,第3组的人数,第4组人数都多于20,且频率之比为,
所以用分层抽样的方法在第3、4两组市民抽取5名参加座谈,
所以应从第3,4组中分别抽取3人,2人.
记第3组的3名分别为,,,第4组的2名分别为,,则从5名中选取2名作重点发言的所有情况为,,,,,,,,,,共有10种.
其中第4组的2名,至少有一名被选中的有:,,,,,,,共有7种,
所以至少有一人的年龄在内的概率为.
18.(1)
(2)
(3)
【详解】(1)如图,连接,
因为为线段的中点,,
所以,因为,所以,
由向量的加法法则得,
故,即成立.
(2)由于,可得,又有,
所以;
,故.
(3)由向量的减法法则得,
由于,可得,又有,
得到,故,
则,
由上问得,故.
19.(1)见详解;(2) .
【详解】(1)证:,,又因为和粘在一起.
,A,C,G,D四点共面.
又.
平面BCGE,平面ABC,平面ABC平面BCGE,得证.
(2)过B作延长线于H,连结AH,因为AB平面BCGE,所以
而又,故平面,所以.又因为所以是二面角的平面角,而在中,又因为故,所以.
而在中,,即二面角的度数为.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列各式的运算结果为纯虚数的是( )
A. B. C. D.
2.已知篮球运动员甲、乙的罚球命中率分别为0.9,0.8,且两人罚球是否命中相互独立.若甲、乙各罚球一次,则恰有一人命中的概率为( )
A.0.26 B.0.28 C.0.72 D.0.98
3.在中,角的对边分别为,若,则的形状为( )
A.直角三角形 B.等腰三角形 C.等腰直角三角形 D.等边三角形
4.在正方体中,为棱的中点,则异面直线与所成角的正切值为
A. B. C. D.
5.从长度分别为3,4,5,6的4条线段中任取3条,能构成钝角三角形的概率为( )
A. B. C. D.
6.已知分别为内角的对边,的面积,则( )
A. B. C. D.
7.甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为,侧面积分别为和,体积分别为和.若,则( )
A. B. C. D.
二、多选题
8.已知表示两条不同直线,a表示平面,则下列选项正确的是( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
9.有一组样本数据,其中是最小值,是最大值,则( )
A.的平均数等于的平均数
B.的中位数等于的中位数
C.的标准差不小于的标准差
D.的极差不大于的极差
10.已知向量,,则( )
A. B.
C. D.在方向上的投影向量的坐标为
11.如图,正方体的棱长为2,是棱的中点,是侧面上的动点,且满足,则下列结论中正确的是( )
A.平面截正方体所得截面面积为
B.点的轨迹长度为
C.存在点,使得
D.直线与平面所成角的正弦值的最大值为
三、填空题
12.已知平面内有、、、四点,其中,,三点共线,且,则 .
13.已知三棱锥的所有顶点都在球O的球面上,SC是球O的直径若平面平面SCB,,,三棱锥的体积为9,则球O的表面积为 .
14.的内角,,的对边分别为,,,已知,,,则的最大值为 .
四、解答题
15.已知复数满足
(1)求复数
(2)若复数是关于的方程的一个根,求,的值
16.在中,内角A,B,C的对边a,b,c,且,已知,,,求:
(1)a和c的值;
(2)的值.
17.某研究机构为了了解各年龄层对高考改革方案的关注程度,随机选取了200名年龄在内的市民进行了调查,并将结果绘制成如图所示的频率分布直方图(分第一~五组区间分别为,,,,,).
(1)求选取的市民年龄在内的人数;
(2)利用频率分布直方图,估计200名市民的年龄的平均数和第80百分位数;
(3)若从第3,4组用分层抽样的方法选取5名市民进行座谈,再从中选取2人在座谈会中作重点发言,求作重点发言的市民中至少有一人的年龄在内的概率.
18.如图,在梯形中,,,,为线段的中点,记,.
(1)用,表示向量;
(2)求的值;
(3)求与夹角的余弦值.
19.图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.
(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的二面角B CG A的大小.
安徽省合肥市百花中学等四校联考2024-2025学年高一下学期期末考试数学试题参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B C C C C BD BD ACD
题号 11
答案 AC
1.B
详解:,,,,
通过比较可以知道,只有为纯虚数,故选B.
2.A
【详解】设“篮球运动员甲、乙的罚球命中”分别为事件A,B,“恰有一人命中”为事件C,
则
.
故选:A.
3.B
【详解】因,由正弦定理,,即,
因,则,故, ,即,故是等腰三角形.
故选:B.
4.C
【详解】在正方体中,,所以异面直线与所成角为,
设正方体边长为,则由为棱的中点,可得,所以,
则.故选C.
5.C
【详解】从4条线段中取3条的组合数为:,具体为:①3,4,5;②3,4,6;③3,5,6;④4,5,6.
设三角形边长为a,b,c,c为最大边,则:
钝角三角形的满足条件为:.
组合①:
组合②:
组合③:
组合④:
综上,满足钝角三角形的组合数为2,概率.
故选:C.
6.C
【详解】由余弦定理得,
又三角形面积公式得,
故,
又,故,即,
又,故.
故选:C
7.C
【详解】设甲、乙两个圆锥的母线长均为,底面半径分别为,
则,所以①,
因为侧面展开图的圆心角之和为,
所以,即②,
由①②解得,
所以甲圆锥的高,乙圆锥的高,
所以.
故选:C.
8.BD
【详解】对于A,若,,则或者异面,或者相交,故A错误,
对于B,若,,则,故B正确,
对于C,若,,则或者,故C错误,
对于D,若,,则,D正确,
故选:BD
9.BD
【详解】对于A,不妨取为,其平均数为,
为,其平均数为1,
此时的平均数不等于的平均数,A错误;
对于B,不妨设,则中位数为,
的中位数也为,故B正确;
对于C,取为,平均数为,
其标准差为,
即为,平均数为,
则其标准差为,
因为,所以,
此时的标准差小于的标准差,故C错误;
对于D,不妨设,
则,当且仅当时等号成立,
即的极差不大于的极差,故D正确.
故选:BD.
10.ACD
【详解】选项A:已知向量,,
所以,,故A对;
选项B:因为,而,故B错;
选项C:因为,,故C对;
选项D:根据投影向量公式:,故D对.
故选:ACD.
11.AC
【详解】
已知正方体的棱长为2,是棱的中点,是侧面上的动点,
且满足,取的中点G,连接、,
则等腰梯形(,且)为其截面,
面积为,故A对;
取中点M,中点N,连接,,,
由题可得,,且平面,
所以平面,平面,
又与是平面内的两条相交直线,
所以平面平面,所以点F的运动轨迹为线段,长度为,故B错;
取中点F,因为为等腰三角形,所以,
又因为,所以,故C对.
因为平面,所以为与平面所成的线面角,
所以,
因为,且时最小,满足题设正弦值最大,
所以,,故D错.
故选:AC.
12.1
【详解】因为,,三点共线,所以存在使得
由
所以
即
故答案为:1
13.36π
【详解】三棱锥S ABC的所有顶点都在球O的球面上,SC是球O的直径,
若平面SCA⊥平面SCB,SA=AC,SB=BC,三棱锥S ABC的体积为9,
可知三角形SBC与三角形SAC都是等腰直角三角形,设球的半径为r,
可得 ,解得r=3.
球O的表面积为: .
14.
【详解】由题得,
因为,
所以,
所以,
因为,所以.
由正弦定理得.
所以
,
所以的最大值为,此时.
故答案为:
15.(1)
(2)
【详解】(1)因为,
所以.
(2)因为复数是关于的方程的一个根,
所以,
所以,解得.
16.(1);(2)
【详解】
(1)由得,,又,所以ac=6.
由余弦定理,得.
又b=3,所以.
解,得a=2,c=3或a=3,c=2.
因为a>c,∴ a=3,c=2.
(2)在中,
由正弦定理,得,又因为,所以C为锐角,因此.
于是=.
考点:1.解三角形;2.三角恒等变换.
17.(1)20
(2)平均数32.25; 第80百分位数37.5
(3)
【详解】(1)(1)由题意可知,年龄在内的频率为,
故年龄在内的市民人数为.
(2)(2) 平均数为
32.25;
前三组的频率和为,
第四组的频率为,所以第80百分位数在第四组,
第80百分位数为.
(3)(3)易知,第3组的人数,第4组人数都多于20,且频率之比为,
所以用分层抽样的方法在第3、4两组市民抽取5名参加座谈,
所以应从第3,4组中分别抽取3人,2人.
记第3组的3名分别为,,,第4组的2名分别为,,则从5名中选取2名作重点发言的所有情况为,,,,,,,,,,共有10种.
其中第4组的2名,至少有一名被选中的有:,,,,,,,共有7种,
所以至少有一人的年龄在内的概率为.
18.(1)
(2)
(3)
【详解】(1)如图,连接,
因为为线段的中点,,
所以,因为,所以,
由向量的加法法则得,
故,即成立.
(2)由于,可得,又有,
所以;
,故.
(3)由向量的减法法则得,
由于,可得,又有,
得到,故,
则,
由上问得,故.
19.(1)见详解;(2) .
【详解】(1)证:,,又因为和粘在一起.
,A,C,G,D四点共面.
又.
平面BCGE,平面ABC,平面ABC平面BCGE,得证.
(2)过B作延长线于H,连结AH,因为AB平面BCGE,所以
而又,故平面,所以.又因为所以是二面角的平面角,而在中,又因为故,所以.
而在中,,即二面角的度数为.
同课章节目录
