江苏省常州市2024-2025学年七年级下学期期末考试数学试卷(含答案)
文档属性
| 名称 | 江苏省常州市2024-2025学年七年级下学期期末考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 15:32:01 | ||
图片预览




文档简介
江苏省常州市2024--2025学年下学期七年级数学期末试卷
一、单选题
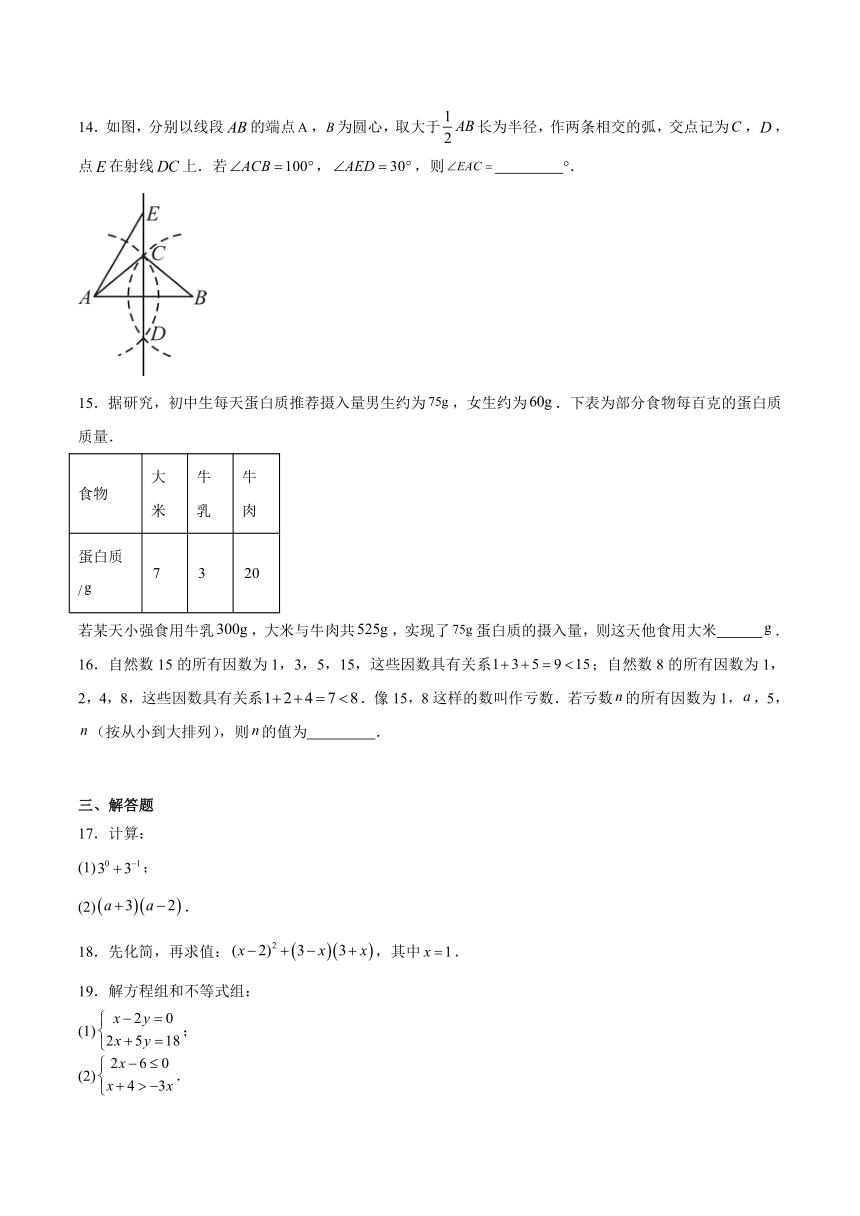
1.下列与消防相关的图标中,是轴对称图形的是( )
A. B.
C. D.
2.如图,左、右托盘中黑球的质量分别为a,b,白球的质量为c,图中体现的数学原理可表示为( )
A.若,则 B.若,则
C.若,则 D.若,则
3.下列运算中正确的是( )
A. B.
C. D.
4.如图,记钟面上数字12,3,5,6,9对应的点分别为点A,B,C,D,E,则点A关于钟面中心O的对称点为( )
A.点B B.点C C.点D D.点E
5.在《九章算术》中记载了这样一道题,大意是:“五头牛和两只羊,价值十两金;两头牛和五只羊,价值八两金.一头牛、一只羊分别价值几两金?”若设一头牛价值两金,一只羊价值两金,则根据题意可列方程组为( )
A. B.
C. D.
6.若要说明命题“如果,那么”是假命题,则可以举反例为( )
A., B.,
C., D.,
7.将三角形纸片与量角器按如图所示方式放置,,,是的外角,则计算的结果为( )
A. B. C. D.
8.已知,其中,,,是正整数,则下列说法中正确的是( )
A.是偶数 B.是偶数
C.是偶数 D.是奇数,是偶数
二、填空题
9.根据图示,写出关于的不等式的解集为 .
10.若,则□中的代数式为 .
11.命题“如果或,那么”的逆命题是 .
12.水痘是冬春季常见的传染病,传播途径主要是呼吸道飞沫或直接接触传染,接触污染的用物也会间接传染.水痘-带状疱疹病毒,直径为.数据用科学记数法表示为 .
13.在中,,,则 .
14.如图,分别以线段的端点,为圆心,取大于长为半径,作两条相交的弧,交点记为,,点在射线上.若,,则 °.
15.据研究,初中生每天蛋白质推荐摄入量男生约为,女生约为.下表为部分食物每百克的蛋白质质量.
食物 大米 牛乳 牛肉
蛋白质/
若某天小强食用牛乳,大米与牛肉共,实现了蛋白质的摄入量,则这天他食用大米 .
16.自然数15的所有因数为1,3,5,15,这些因数具有关系;自然数8的所有因数为1,2,4,8,这些因数具有关系.像15,8这样的数叫作亏数.若亏数的所有因数为1,,5,(按从小到大排列),则的值为 .
三、解答题
17.计算:
(1);
(2).
18.先化简,再求值:,其中.
19.解方程组和不等式组:
(1);
(2).
20.已知:如图,在五边形中,.求证:.
21.证明:连续五个自然数的平方和是5的倍数.
22.如图为由等边三角形组成的网格纸.
(1)先画出关于直线m对称的,再画出关于直线n对称的;
(2)在(1)的条件下,可以看做由绕 顺时针旋转()得到,则的值为 .
23.如图为常州奥林匹克体育中心停车场收费标准(收费期间,不满15分钟部分按15分钟计算),本题中涉及的车辆均为非新能源车辆和非公(任)务车辆,且不享受图中的“收费优惠”.例如,一辆小型车和一辆大型车均连续停车3小时23分钟,则停车费分别为4元和8元.
(1)一辆小型车连续停车5小时,则停车费为 元;一辆大型车连续停车5小时,则停车费为 元;
(2)现一团队有小型车与大型车共6辆,同时连续停车5小时后共收费70元,求小型车与大型车各有多少辆?
(3)若一天中一辆小型车连续停车时间为小时,且停车费为12元,则的取值范围是 .
24.定义:若关于,的二元一次方程的一个解为,当时,则称为二元一次方程的“系相关解”.例如:是二元一次方程的“2系相关解”.
(1)二元一次方程的“1系相关解”为 ;
(2)下列二元一次方程存在“2系相关解”的是 (填序号);
①;②;③.
(3)为二元一次方程的“系相关解”,且,求的取值范围.
25.综合与实践
【问题情境】
如图1,在长方形中,,点E在边上,且.
【初步探究】
(1)如图2,连接,将长方形沿方向平移,得到长方形,连接,则四边形的面积是 ,与的数量关系是 ;
【拓展延伸】
(2)如图3,将长方形绕点E顺时针旋转,得到长方形.
①若旋转过程中,长方形与长方形重叠部分的图形为轴对称图形,请利用直尺与圆规在图4和图5中分别作出点C'(不写作法,保留作图痕迹,作出其中的2种情况),并写出对应的旋转角;
②若旋转过程中,边与边相交于点P,且,求的值.
参考答案
1.C
解:A,B,D选项中的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
C选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形.
故选:C.
2.A
解:由作图可知:,由右图可知:,即A选项符合题意.
故选:A.
3.B
解:A:,故错误.
B:,正确.
C:,故错误.
D:,故错误.
故选B.
4.C
解:记钟面上数字12,3,5,6,9对应的点分别为点A,B,C,D,E,则点A关于钟面中心O的对称点为D,
故选:C
5.A
解:设一头牛价值两金,一只羊价值两金,
由题意得,,
故选:A.
6.B
解:A:,.此时,且,符合原命题,不能作为反例.
B:,.计算得,,满足,但,符合反例要求.
C:,.此时,且,符合原命题,不能作为反例.
D:,.计算得,,不满足,不符合条件.
故选:B.
7.D
解:∵,
∴,
∴,
∴,
故选:D.
8.B
∵,且左边为完全平方数,
∴必为偶数.
∵,且为偶数,
∴也需为偶数.
若为偶数,为偶数,则需为偶数;
若为奇数,为奇数,则需为奇数.
∴与奇偶性相同,
∴必为偶数.
A:如为奇数时,可能为奇数,错误;
B:是偶数,正确;
C:的奇偶性由决定,不一定为偶数;
D:的奇偶性不确定,错误.
故选:B.
9.
解:图示的不等式的解集为.
故答案为:
10.
解:由可得,,
故答案为:.
11.如果,那么或
解:命题“如果或,那么”的逆命题是:如果,那么或.
故答案为:如果,那么或.
12.
解∶ .
故答案为∶
13.55
解:在中,,则,
,
,即,
解得,
故答案为:.
14.20
解:根据题意可知,垂直平分线段,
,
,
,
,
故答案为:20.
15.
解:设这天他食用大米,则食用牛肉,
由题意得,,
解得,
∴这天他食用大米,
故答案为:.
16.10或15
解:亏数的所有因数为1,,5,(按从小到大排列),
,即可取,
当时,;
当时,;
当时,,此时所有因数为,不符合题意,舍去;
综上所述,的值为10或15,
故答案为:10或15.
17.(1);
(2).
(1)解:
;
(2)解:
.
18.
解:,
;
时,
原式
.
19.(1)
(2)
(1)解:
由①得③,
将③代入②得,
解得;
将代入③得;
原方程组的解是;
(2)解:,
解不等式①得;
解不等式②得;
不等式组的解集为.
20.见解析
证明:∵五边形的内角和等于,
∴.
∵,
∴.
∴.
21.见解析
证明:设五个自然数为,,,,(),
则
=
=.
∵是整数,
∴是5的倍数.
∴连续五个自然数的平方和是5的倍数.
22.(1)见解析
(2)点,120
(1)解:画图如下.
;
(2)解:由等边三角形的性质可得:,
在(1)的条件下,可以看做由绕点顺时针旋转()得到,则的值为.
23.(1)7,14
(2)小型车2辆,大型车4辆
(3)
(1)解:由表可知,小型车首1小时是3元,超过则每15分钟元(大型车双倍),
∵一辆小型车连续停车5小时,由于前120分钟免费,因此实际收费是后面2个小时,
∴费用为(元),
∵大型车是小型车的双倍,
∴大型车费用为14元;
故答案为:7;14.
(2)设小型车辆,大型车辆,则
解这个方程组,得,
答:小型车2辆,大型车4辆.
(3),,且每个小时有4个15分钟,
∴1小时收费以外的时间为小时(收费期间,不满15分钟部分按15分钟计算),
∵,
∴,24小时连续停放只收12元,
∴.
24.(1)
(2)①,③
(3)
(1)解:设是二元一次方程的“1系相关解”,则得,
解得:,故;
故答案为:;
(2)解:设是二元一次方程的“2系相关解”,即 ;
当时,,解得;
当时,方程组无解;
当时,,解得;
综上,二元一次方程存在“2系相关解”的是①,③;
故答案为:①,③;
(3)解:由题意得,则.
∵,
∴.
解得.
∴.
∴,即.
25.(1)28,(2)①见解析②或310
解:(1)根据平移的性质可得,且,四边形的高为4,
∴四边形的面积是;
连接,
根据平移的性质得,
∴,
∴.
∵,
∴;
故答案为:28,;
(2)①①点C'位置正确,答案不唯一;
②(Ⅰ)∵在长方形中,,
∴.
∴.
∵在长方形中,,
∴,即.
(Ⅱ)∵,
∴.
∵在长方形中,,
∴.
∵在长方形中,,
∴.
∴.
∴或310.
一、单选题
1.下列与消防相关的图标中,是轴对称图形的是( )
A. B.
C. D.
2.如图,左、右托盘中黑球的质量分别为a,b,白球的质量为c,图中体现的数学原理可表示为( )
A.若,则 B.若,则
C.若,则 D.若,则
3.下列运算中正确的是( )
A. B.
C. D.
4.如图,记钟面上数字12,3,5,6,9对应的点分别为点A,B,C,D,E,则点A关于钟面中心O的对称点为( )
A.点B B.点C C.点D D.点E
5.在《九章算术》中记载了这样一道题,大意是:“五头牛和两只羊,价值十两金;两头牛和五只羊,价值八两金.一头牛、一只羊分别价值几两金?”若设一头牛价值两金,一只羊价值两金,则根据题意可列方程组为( )
A. B.
C. D.
6.若要说明命题“如果,那么”是假命题,则可以举反例为( )
A., B.,
C., D.,
7.将三角形纸片与量角器按如图所示方式放置,,,是的外角,则计算的结果为( )
A. B. C. D.
8.已知,其中,,,是正整数,则下列说法中正确的是( )
A.是偶数 B.是偶数
C.是偶数 D.是奇数,是偶数
二、填空题
9.根据图示,写出关于的不等式的解集为 .
10.若,则□中的代数式为 .
11.命题“如果或,那么”的逆命题是 .
12.水痘是冬春季常见的传染病,传播途径主要是呼吸道飞沫或直接接触传染,接触污染的用物也会间接传染.水痘-带状疱疹病毒,直径为.数据用科学记数法表示为 .
13.在中,,,则 .
14.如图,分别以线段的端点,为圆心,取大于长为半径,作两条相交的弧,交点记为,,点在射线上.若,,则 °.
15.据研究,初中生每天蛋白质推荐摄入量男生约为,女生约为.下表为部分食物每百克的蛋白质质量.
食物 大米 牛乳 牛肉
蛋白质/
若某天小强食用牛乳,大米与牛肉共,实现了蛋白质的摄入量,则这天他食用大米 .
16.自然数15的所有因数为1,3,5,15,这些因数具有关系;自然数8的所有因数为1,2,4,8,这些因数具有关系.像15,8这样的数叫作亏数.若亏数的所有因数为1,,5,(按从小到大排列),则的值为 .
三、解答题
17.计算:
(1);
(2).
18.先化简,再求值:,其中.
19.解方程组和不等式组:
(1);
(2).
20.已知:如图,在五边形中,.求证:.
21.证明:连续五个自然数的平方和是5的倍数.
22.如图为由等边三角形组成的网格纸.
(1)先画出关于直线m对称的,再画出关于直线n对称的;
(2)在(1)的条件下,可以看做由绕 顺时针旋转()得到,则的值为 .
23.如图为常州奥林匹克体育中心停车场收费标准(收费期间,不满15分钟部分按15分钟计算),本题中涉及的车辆均为非新能源车辆和非公(任)务车辆,且不享受图中的“收费优惠”.例如,一辆小型车和一辆大型车均连续停车3小时23分钟,则停车费分别为4元和8元.
(1)一辆小型车连续停车5小时,则停车费为 元;一辆大型车连续停车5小时,则停车费为 元;
(2)现一团队有小型车与大型车共6辆,同时连续停车5小时后共收费70元,求小型车与大型车各有多少辆?
(3)若一天中一辆小型车连续停车时间为小时,且停车费为12元,则的取值范围是 .
24.定义:若关于,的二元一次方程的一个解为,当时,则称为二元一次方程的“系相关解”.例如:是二元一次方程的“2系相关解”.
(1)二元一次方程的“1系相关解”为 ;
(2)下列二元一次方程存在“2系相关解”的是 (填序号);
①;②;③.
(3)为二元一次方程的“系相关解”,且,求的取值范围.
25.综合与实践
【问题情境】
如图1,在长方形中,,点E在边上,且.
【初步探究】
(1)如图2,连接,将长方形沿方向平移,得到长方形,连接,则四边形的面积是 ,与的数量关系是 ;
【拓展延伸】
(2)如图3,将长方形绕点E顺时针旋转,得到长方形.
①若旋转过程中,长方形与长方形重叠部分的图形为轴对称图形,请利用直尺与圆规在图4和图5中分别作出点C'(不写作法,保留作图痕迹,作出其中的2种情况),并写出对应的旋转角;
②若旋转过程中,边与边相交于点P,且,求的值.
参考答案
1.C
解:A,B,D选项中的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
C选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形.
故选:C.
2.A
解:由作图可知:,由右图可知:,即A选项符合题意.
故选:A.
3.B
解:A:,故错误.
B:,正确.
C:,故错误.
D:,故错误.
故选B.
4.C
解:记钟面上数字12,3,5,6,9对应的点分别为点A,B,C,D,E,则点A关于钟面中心O的对称点为D,
故选:C
5.A
解:设一头牛价值两金,一只羊价值两金,
由题意得,,
故选:A.
6.B
解:A:,.此时,且,符合原命题,不能作为反例.
B:,.计算得,,满足,但,符合反例要求.
C:,.此时,且,符合原命题,不能作为反例.
D:,.计算得,,不满足,不符合条件.
故选:B.
7.D
解:∵,
∴,
∴,
∴,
故选:D.
8.B
∵,且左边为完全平方数,
∴必为偶数.
∵,且为偶数,
∴也需为偶数.
若为偶数,为偶数,则需为偶数;
若为奇数,为奇数,则需为奇数.
∴与奇偶性相同,
∴必为偶数.
A:如为奇数时,可能为奇数,错误;
B:是偶数,正确;
C:的奇偶性由决定,不一定为偶数;
D:的奇偶性不确定,错误.
故选:B.
9.
解:图示的不等式的解集为.
故答案为:
10.
解:由可得,,
故答案为:.
11.如果,那么或
解:命题“如果或,那么”的逆命题是:如果,那么或.
故答案为:如果,那么或.
12.
解∶ .
故答案为∶
13.55
解:在中,,则,
,
,即,
解得,
故答案为:.
14.20
解:根据题意可知,垂直平分线段,
,
,
,
,
故答案为:20.
15.
解:设这天他食用大米,则食用牛肉,
由题意得,,
解得,
∴这天他食用大米,
故答案为:.
16.10或15
解:亏数的所有因数为1,,5,(按从小到大排列),
,即可取,
当时,;
当时,;
当时,,此时所有因数为,不符合题意,舍去;
综上所述,的值为10或15,
故答案为:10或15.
17.(1);
(2).
(1)解:
;
(2)解:
.
18.
解:,
;
时,
原式
.
19.(1)
(2)
(1)解:
由①得③,
将③代入②得,
解得;
将代入③得;
原方程组的解是;
(2)解:,
解不等式①得;
解不等式②得;
不等式组的解集为.
20.见解析
证明:∵五边形的内角和等于,
∴.
∵,
∴.
∴.
21.见解析
证明:设五个自然数为,,,,(),
则
=
=.
∵是整数,
∴是5的倍数.
∴连续五个自然数的平方和是5的倍数.
22.(1)见解析
(2)点,120
(1)解:画图如下.
;
(2)解:由等边三角形的性质可得:,
在(1)的条件下,可以看做由绕点顺时针旋转()得到,则的值为.
23.(1)7,14
(2)小型车2辆,大型车4辆
(3)
(1)解:由表可知,小型车首1小时是3元,超过则每15分钟元(大型车双倍),
∵一辆小型车连续停车5小时,由于前120分钟免费,因此实际收费是后面2个小时,
∴费用为(元),
∵大型车是小型车的双倍,
∴大型车费用为14元;
故答案为:7;14.
(2)设小型车辆,大型车辆,则
解这个方程组,得,
答:小型车2辆,大型车4辆.
(3),,且每个小时有4个15分钟,
∴1小时收费以外的时间为小时(收费期间,不满15分钟部分按15分钟计算),
∵,
∴,24小时连续停放只收12元,
∴.
24.(1)
(2)①,③
(3)
(1)解:设是二元一次方程的“1系相关解”,则得,
解得:,故;
故答案为:;
(2)解:设是二元一次方程的“2系相关解”,即 ;
当时,,解得;
当时,方程组无解;
当时,,解得;
综上,二元一次方程存在“2系相关解”的是①,③;
故答案为:①,③;
(3)解:由题意得,则.
∵,
∴.
解得.
∴.
∴,即.
25.(1)28,(2)①见解析②或310
解:(1)根据平移的性质可得,且,四边形的高为4,
∴四边形的面积是;
连接,
根据平移的性质得,
∴,
∴.
∵,
∴;
故答案为:28,;
(2)①①点C'位置正确,答案不唯一;
②(Ⅰ)∵在长方形中,,
∴.
∴.
∵在长方形中,,
∴,即.
(Ⅱ)∵,
∴.
∵在长方形中,,
∴.
∵在长方形中,,
∴.
∴.
∴或310.
同课章节目录
