第一章 特殊平行四边形 自主检测同步练习(含答案)2025-2026学年北师大版数学九年级上册
文档属性
| 名称 | 第一章 特殊平行四边形 自主检测同步练习(含答案)2025-2026学年北师大版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 214.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 18:09:36 | ||
图片预览



文档简介
第一章特殊平行四边形自主检测
一、选择题(每小题6分,共42分)
1.「2025安徽宿州萧县期中」菱形、矩形、正方形都具有的性质是 ( )
A.邻边相等 B.四个角都是直角
C.对角线互相垂直 D.对角线互相平分
2.「2025安徽宿州泗县月考」数学课上,老师在投影屏上出示下面的抢答题,需要同学们回答特殊图形可以代表的内容.
如图,四边形ABCD 是平行四边形,①当※时,平行四边形 ABCD 是矩形.②当◎时,平行四边形ABCD是矩形.③当▲时,平行四边形ABCD 是菱形.④当◆时,平行四边形ABCD 是正方形.则下列回答不正确的是 ( )
A.※可以代表∠ABC=90°
B.◎可以代表AC=BD
C.▲可以代表AB=BC
D.●可以代表AC⊥BD
3.「2025四川成都七中月考」如图,四边形ABCD 是菱形,对角线AC=4 cm,BD=2cm,DH⊥AB 于点 H,则DH的长为 ( )
C.cm
4.「2024山东东营中考」如图,四边形ABCD 是矩形,直线EF分别交AD,BC,BD于点E,F,O,选项的条件中,不能证明△BOF≌△DOE 的是 ( )
A. O 为矩形ABCD 两条对角线的交点
B. EO=FO
C. AE=CF
D. EF⊥BD
5.「2024河南郑州一中月考」如图,在 Rt△ABC 中,∠A=90°,P 为边 BC 上一动点,PE⊥AB 于 E,PF⊥AC于 F,则在动点 P 从点 B 出发,沿着 BC 匀速向终点 C 运动的过程中,线段 EF的长度的大小变化情况是 ( )
A.一直增大 B.一直减小
C.先减小后增大 D.先增大后减少
6.「2024重庆中考B卷」如图,在边长为4的正方形ABCD 中,点E是BC 上一点,点 F是CD 延长线上一点,连接AE,AF,AM 平分∠EAF 交 CD 于点M.若BE=DF=1,则 DM 的长度为 ( )
A.2 B. C. D.
7.「2024浙江温州二中月考」如图,在正方形ABCD 中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q在对角线 BD 上,且四边形 MNPQ 和四边形AEFG均为正方形,则 等于 ( )
C. D.
二、填空题(每小题6分,共18分)
8.如图,三位同学分别站在一个直角三角形的三个顶点处做投圈游戏,目标物放在斜边AC 的中点O处,已知AC=6m,则点B到目标物的距离是 m.
9.新实践操作题「2025河南平顶山期中」小明用四根长度相等的木条制作了能够活动的菱形学具,他先将学具活动成如图(1)所示的菱形,并测得∠ABC=60°,接着将学具活动成如图(2)所示的正方形,并测得对角线. ,则图(1)中菱形的对角线 BD 的长为 .
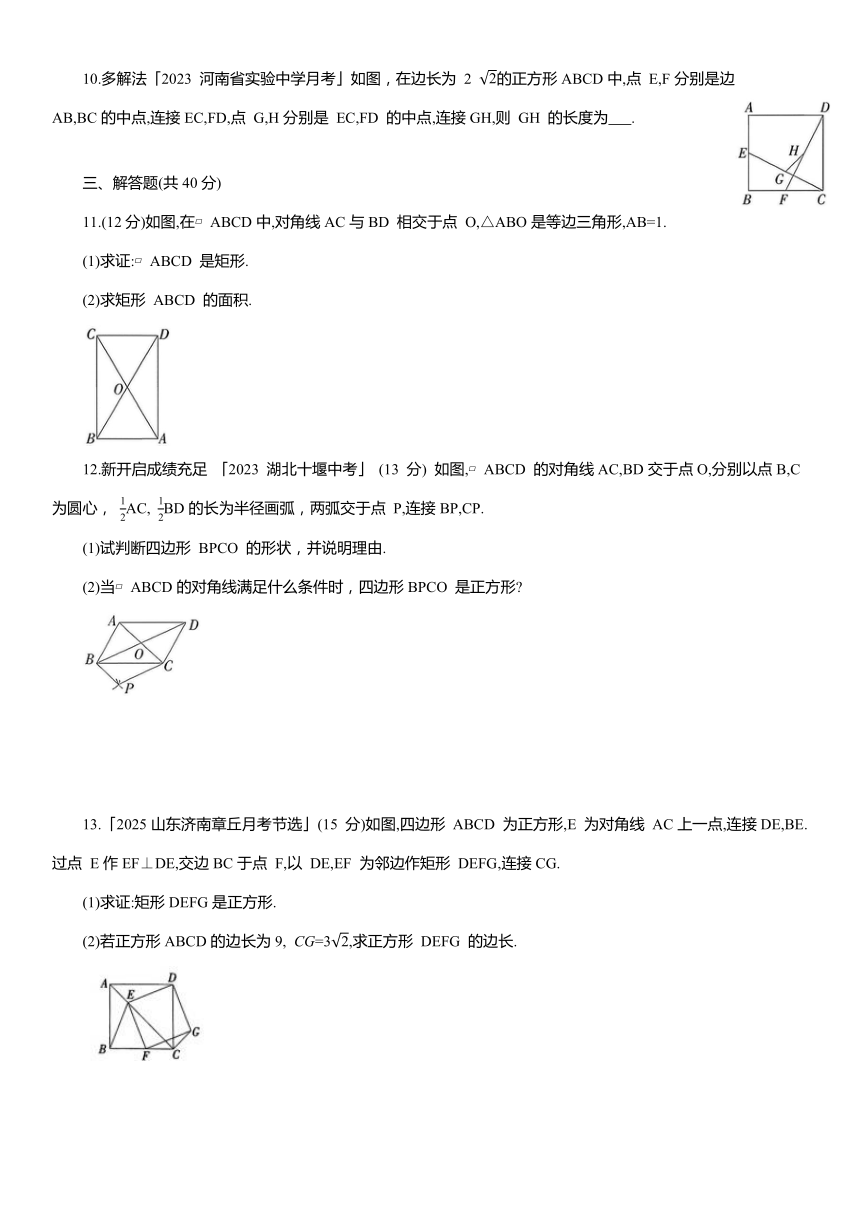
10.多解法「2023 河南省实验中学月考」如图,在边长为 2 的正方形ABCD中,点 E,F分别是边AB,BC的中点,连接EC,FD,点 G,H分别是 EC,FD 的中点,连接GH,则 GH 的长度为 .
三、解答题(共40分)
11.(12分)如图,在 ABCD中,对角线AC与BD 相交于点 O,△ABO是等边三角形,AB=1.
(1)求证: ABCD 是矩形.
(2)求矩形 ABCD 的面积.
12.新开启成绩充足 「2023 湖北十堰中考」 (13 分) 如图, ABCD 的对角线AC,BD交于点O,分别以点B,C 为圆心, AC, BD的长为半径画弧,两弧交于点 P,连接BP,CP.
(1)试判断四边形 BPCO 的形状,并说明理由.
(2)当 ABCD的对角线满足什么条件时,四边形BPCO 是正方形
13.「2025山东济南章丘月考节选」(15 分)如图,四边形 ABCD 为正方形,E 为对角线 AC上一点,连接DE,BE.过点 E作EF⊥DE,交边BC于点 F,以 DE,EF 为邻边作矩形 DEFG,连接CG.
(1)求证:矩形DEFG是正方形.
(2)若正方形ABCD的边长为9, 求正方形 DEFG 的边长.
答案
1. D矩形、菱形、正方形都属于平行四边形,所以矩形、菱形、正方形一定都具有的性质是所有平行四边形都具有的性质,所有平行四边形的对角线互相平分,∴ A,B,C选项不符合题意,D选项符合题意,故选 D.
2. D 选项A,∵四边形ABCD 是平行四边形,∠ABC=90°,∴平行四边形ABCD 是矩形,∴A不符合题意;选项B,∵ 四边形ABCD 是平行四边形,AC=BD,∴平行四边形ABCD 是矩形,.. B 不符合题意;选项 C,.四边形ABCD 是平行四边形,AB=BC,∴平行四边形ABCD是菱形,.. C 不符合题意;选项 D,∵ 四边形ABCD 是平行四边形,AC⊥BD,∴平行四边形ABCD是菱形,但不一定是正方形,∴D符合题意.故选 D.
3B ∵ 四边形 ABCD 是菱形,∴AC⊥BD,OA=OC= BD=AB·DH,∴ 故选 B.
4. D ∵ 四边形 ABCD 是矩形,∴AD=BC,AD∥BC,
..∠OBF=∠ODE,∠OFB=∠OED.选项 A,∵O 为矩
形ABCD两条对角线的交点,∴OB=OD.在△BOF 和△DOE 中,
(AAS),故A不符合题意;选项B,在△BOF 和△DOE中,
不符合题意;选项 C,∴AE=CF,∴BC-CF=AD-AE,即
BF =DE,
在 △BOF和△DOE中,
. △BOF≌△DOE(ASA),故 C 不
符合题意;选项 D,∵ EF ⊥BD,∴∠BOF =∠DOE
不能证明△BOF≌△DOE,故D符合题意.故选 D.
5. C 如图,连接AP.∵ ∠BAC=90°,PE⊥AB,PF⊥AC,∴四边形AFPE 是矩形,∴ EF=AP,由垂线段最短可得AP⊥BC时,AP 最短,此时线段 EF的长度最小,∴在动点 P 从点 B 出发,沿着 BC 匀速向终点 C 运动的过程中,线段 EF的长度的大小变化情况是先减小后增大.故选C.
方法解读 本题考查了矩形的判定与性质以及垂线段最短的性质.判断出“当AP⊥BC时,线段EF的长度最小”是解题的关键.
6D ∵ 四边形ABCD 是正方形,∴ AB=AD,∠ABE=90°,∠ADF=180°-∠ADM =90°.在△ABE 和△ADF
中
·AE=AF.∵ AM 平分∠EAF,∴ ∠EAM = ∠FAM.在△AEM 和△AFM 中, △AFM(SAS),∴EM=FM.
四边形 ABCD 是正方形,∴ BC = CD = 4,∠BCD=90°,
设DM=x,则MC=CD-DM=4-x,CE=BC-BE=4-1=3,EM=FM=FD+DM=1+x.
在 Rt△MCE中,根据勾股定理,得 即 解得
故选 D.
7. D ∵ 四边形 ABCD 是正方形,∴ ∠ABD=∠CBD=45°,∵ 四边形 MNPQ 和四边形 AEFG均为正方形,∴∠BEF = ∠AEF = 90°, ∠BMN = ∠QMN = 90°,∴△BEF和△BMN都是等腰直角三角形,∴ BE=FE= 同理可得DQ=MQ,
故选 D.
8.答案
解析 ∵ ∠ABC=90°,O 是斜边AC的中点,
9.答案
解析 在正方形 ABCD 中,∠ABC=90°,∴AB +CB =AC AB=CB,AC=20 ,∴AB=BC=20.在题图(1)中,连接AC交 BD 于点O(图略),
在菱形 ABCD 中,AC⊥BD,AB=BC=20,∵ ∠ABC=60°,∴△ABC 为等边三角形,∴∠ABO=30°,∴ OA= 20 ,故答案为20
10 .答案
解析 【解法一】连接 CH 并延长交 AD 于 P,连接PE,如图1,∵ 四边形 ABCD 是正方形,且边长为
..∠A=90°,AD∥BC,AB=AD=BC=2 ,∵E,F分别是边AB,BC 的中点,. ∵ 点 H 是 FD 的中点,∴ DH = FH,∵ AD∥BC,.∠DPH=∠FCH,又∵∠DHP =∠FHC,∴△PDH≌△CFH(AAS),∴PD=CF= ,PH=CH,即H是CD的中点,..
·点G,H分别是EC,CP的中点,∴
【解法二】如图2,连接 GF,可得 GF∥BE.作 GM⊥DC 于 M,可得四边形 GFCM 为矩形,所以 延长GH交CD 于N,可得△GHF≌△NHD,所以 所以. 由勾股定理可求出GN=2,从而得到GH=1.
【解法三】如图3,连接 EH 并延长,交 CD 于点 M,连接 FG 并延长,交 EH 于点 O,交 AD 于点 N.易知△OGH为等腰直角三角形, 所以GH=1.
【解法四】如图4,连接FG并延长至点O,使OG=GF,连接BD,易知点 O 为正方形对角线的交点,GH 是△OFD 的中位线,所以
【解法五】如图5,建立如图所示的平面直角坐标系.易知E(0, ),C(2 ,0),F( ,0),D(2 ,2 所以
所以
【解法六】如图6,根据图形特性,将图形放在格点图中,小正方形的边长为 ,观察可得GH=1.
11.解析 (1)证明:∵ △ABO 是等边三角形,∴OA =OB=AB,∵四边形ABCD 是平行四边形,∴OA=OC,OB=OD,.. OA=OC=OB=OD,∴AC=BD,∴四边形ABCD 是矩形.
(2)∵ 四边形 ABCD 是矩形,.. ∠ABC=90°,AC=2AO,∵AB=1,∴AO=1,∴AC=2,由勾股定理得 ∴矩形 ABCD 的面积
12.解析 (1)四边形 BPCO 为平行四边形.
理由:∵四边形 ABCD 为平行四边形,∴OC=OA= ∵分别以点 B,C为圆心, AC, BD的长为半径画弧,两弧交于点 P,∴OB=CP,BP=OC,∴四边形 BPCO为平行四边形.
(2)当AC⊥BD,AC=BD时,四边形 BPCO 为正方形.·AC⊥BD,∴∠BOC=90°,.. BPCO为矩形. .矩形 BPCO 为正方形.
13.解析 (1)证明:如图 1,作 EM⊥BC 于 M,EN⊥CD于 N,易知四边形 EMCN 是矩形,
,、∠MEN=90°,
∵点 E 是正方形ABCD 对角线上的点,∴EM=EN,
∵∠DEF=90°,∴∠DEN=∠MEF=90°-∠FEN,在△DEN和△FEM中, ∴△DEN≌△FEM(ASA),∴ EF=DE,∴矩形 DEFG是正方形.
(2)∵ 四边形 DEFG和四边形ABCD 是正方形,.. DE = DG,AD= DC, . ∠CDG+∠CDE = ∠ADE+∠CDE=90°,..∠CDG=∠ADE,在△ADE和△CDG中,
.. △ADE≌△CDG(SAS),
.. AE=CG,∠DAE=∠DCG=45°,
··∠ACD=45°,∴∠ACG=∠ACD+∠DCG=90°,
.. CE⊥CG,.. CE+CG=CE+AE=AC= AB=9
如图2,连接EG,
,正方形 DEFG的边长为3
一、选择题(每小题6分,共42分)
1.「2025安徽宿州萧县期中」菱形、矩形、正方形都具有的性质是 ( )
A.邻边相等 B.四个角都是直角
C.对角线互相垂直 D.对角线互相平分
2.「2025安徽宿州泗县月考」数学课上,老师在投影屏上出示下面的抢答题,需要同学们回答特殊图形可以代表的内容.
如图,四边形ABCD 是平行四边形,①当※时,平行四边形 ABCD 是矩形.②当◎时,平行四边形ABCD是矩形.③当▲时,平行四边形ABCD 是菱形.④当◆时,平行四边形ABCD 是正方形.则下列回答不正确的是 ( )
A.※可以代表∠ABC=90°
B.◎可以代表AC=BD
C.▲可以代表AB=BC
D.●可以代表AC⊥BD
3.「2025四川成都七中月考」如图,四边形ABCD 是菱形,对角线AC=4 cm,BD=2cm,DH⊥AB 于点 H,则DH的长为 ( )
C.cm
4.「2024山东东营中考」如图,四边形ABCD 是矩形,直线EF分别交AD,BC,BD于点E,F,O,选项的条件中,不能证明△BOF≌△DOE 的是 ( )
A. O 为矩形ABCD 两条对角线的交点
B. EO=FO
C. AE=CF
D. EF⊥BD
5.「2024河南郑州一中月考」如图,在 Rt△ABC 中,∠A=90°,P 为边 BC 上一动点,PE⊥AB 于 E,PF⊥AC于 F,则在动点 P 从点 B 出发,沿着 BC 匀速向终点 C 运动的过程中,线段 EF的长度的大小变化情况是 ( )
A.一直增大 B.一直减小
C.先减小后增大 D.先增大后减少
6.「2024重庆中考B卷」如图,在边长为4的正方形ABCD 中,点E是BC 上一点,点 F是CD 延长线上一点,连接AE,AF,AM 平分∠EAF 交 CD 于点M.若BE=DF=1,则 DM 的长度为 ( )
A.2 B. C. D.
7.「2024浙江温州二中月考」如图,在正方形ABCD 中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q在对角线 BD 上,且四边形 MNPQ 和四边形AEFG均为正方形,则 等于 ( )
C. D.
二、填空题(每小题6分,共18分)
8.如图,三位同学分别站在一个直角三角形的三个顶点处做投圈游戏,目标物放在斜边AC 的中点O处,已知AC=6m,则点B到目标物的距离是 m.
9.新实践操作题「2025河南平顶山期中」小明用四根长度相等的木条制作了能够活动的菱形学具,他先将学具活动成如图(1)所示的菱形,并测得∠ABC=60°,接着将学具活动成如图(2)所示的正方形,并测得对角线. ,则图(1)中菱形的对角线 BD 的长为 .
10.多解法「2023 河南省实验中学月考」如图,在边长为 2 的正方形ABCD中,点 E,F分别是边AB,BC的中点,连接EC,FD,点 G,H分别是 EC,FD 的中点,连接GH,则 GH 的长度为 .
三、解答题(共40分)
11.(12分)如图,在 ABCD中,对角线AC与BD 相交于点 O,△ABO是等边三角形,AB=1.
(1)求证: ABCD 是矩形.
(2)求矩形 ABCD 的面积.
12.新开启成绩充足 「2023 湖北十堰中考」 (13 分) 如图, ABCD 的对角线AC,BD交于点O,分别以点B,C 为圆心, AC, BD的长为半径画弧,两弧交于点 P,连接BP,CP.
(1)试判断四边形 BPCO 的形状,并说明理由.
(2)当 ABCD的对角线满足什么条件时,四边形BPCO 是正方形
13.「2025山东济南章丘月考节选」(15 分)如图,四边形 ABCD 为正方形,E 为对角线 AC上一点,连接DE,BE.过点 E作EF⊥DE,交边BC于点 F,以 DE,EF 为邻边作矩形 DEFG,连接CG.
(1)求证:矩形DEFG是正方形.
(2)若正方形ABCD的边长为9, 求正方形 DEFG 的边长.
答案
1. D矩形、菱形、正方形都属于平行四边形,所以矩形、菱形、正方形一定都具有的性质是所有平行四边形都具有的性质,所有平行四边形的对角线互相平分,∴ A,B,C选项不符合题意,D选项符合题意,故选 D.
2. D 选项A,∵四边形ABCD 是平行四边形,∠ABC=90°,∴平行四边形ABCD 是矩形,∴A不符合题意;选项B,∵ 四边形ABCD 是平行四边形,AC=BD,∴平行四边形ABCD 是矩形,.. B 不符合题意;选项 C,.四边形ABCD 是平行四边形,AB=BC,∴平行四边形ABCD是菱形,.. C 不符合题意;选项 D,∵ 四边形ABCD 是平行四边形,AC⊥BD,∴平行四边形ABCD是菱形,但不一定是正方形,∴D符合题意.故选 D.
3B ∵ 四边形 ABCD 是菱形,∴AC⊥BD,OA=OC= BD=AB·DH,∴ 故选 B.
4. D ∵ 四边形 ABCD 是矩形,∴AD=BC,AD∥BC,
..∠OBF=∠ODE,∠OFB=∠OED.选项 A,∵O 为矩
形ABCD两条对角线的交点,∴OB=OD.在△BOF 和△DOE 中,
(AAS),故A不符合题意;选项B,在△BOF 和△DOE中,
不符合题意;选项 C,∴AE=CF,∴BC-CF=AD-AE,即
BF =DE,
在 △BOF和△DOE中,
. △BOF≌△DOE(ASA),故 C 不
符合题意;选项 D,∵ EF ⊥BD,∴∠BOF =∠DOE
不能证明△BOF≌△DOE,故D符合题意.故选 D.
5. C 如图,连接AP.∵ ∠BAC=90°,PE⊥AB,PF⊥AC,∴四边形AFPE 是矩形,∴ EF=AP,由垂线段最短可得AP⊥BC时,AP 最短,此时线段 EF的长度最小,∴在动点 P 从点 B 出发,沿着 BC 匀速向终点 C 运动的过程中,线段 EF的长度的大小变化情况是先减小后增大.故选C.
方法解读 本题考查了矩形的判定与性质以及垂线段最短的性质.判断出“当AP⊥BC时,线段EF的长度最小”是解题的关键.
6D ∵ 四边形ABCD 是正方形,∴ AB=AD,∠ABE=90°,∠ADF=180°-∠ADM =90°.在△ABE 和△ADF
中
·AE=AF.∵ AM 平分∠EAF,∴ ∠EAM = ∠FAM.在△AEM 和△AFM 中, △AFM(SAS),∴EM=FM.
四边形 ABCD 是正方形,∴ BC = CD = 4,∠BCD=90°,
设DM=x,则MC=CD-DM=4-x,CE=BC-BE=4-1=3,EM=FM=FD+DM=1+x.
在 Rt△MCE中,根据勾股定理,得 即 解得
故选 D.
7. D ∵ 四边形 ABCD 是正方形,∴ ∠ABD=∠CBD=45°,∵ 四边形 MNPQ 和四边形 AEFG均为正方形,∴∠BEF = ∠AEF = 90°, ∠BMN = ∠QMN = 90°,∴△BEF和△BMN都是等腰直角三角形,∴ BE=FE= 同理可得DQ=MQ,
故选 D.
8.答案
解析 ∵ ∠ABC=90°,O 是斜边AC的中点,
9.答案
解析 在正方形 ABCD 中,∠ABC=90°,∴AB +CB =AC AB=CB,AC=20 ,∴AB=BC=20.在题图(1)中,连接AC交 BD 于点O(图略),
在菱形 ABCD 中,AC⊥BD,AB=BC=20,∵ ∠ABC=60°,∴△ABC 为等边三角形,∴∠ABO=30°,∴ OA= 20 ,故答案为20
10 .答案
解析 【解法一】连接 CH 并延长交 AD 于 P,连接PE,如图1,∵ 四边形 ABCD 是正方形,且边长为
..∠A=90°,AD∥BC,AB=AD=BC=2 ,∵E,F分别是边AB,BC 的中点,. ∵ 点 H 是 FD 的中点,∴ DH = FH,∵ AD∥BC,.∠DPH=∠FCH,又∵∠DHP =∠FHC,∴△PDH≌△CFH(AAS),∴PD=CF= ,PH=CH,即H是CD的中点,..
·点G,H分别是EC,CP的中点,∴
【解法二】如图2,连接 GF,可得 GF∥BE.作 GM⊥DC 于 M,可得四边形 GFCM 为矩形,所以 延长GH交CD 于N,可得△GHF≌△NHD,所以 所以. 由勾股定理可求出GN=2,从而得到GH=1.
【解法三】如图3,连接 EH 并延长,交 CD 于点 M,连接 FG 并延长,交 EH 于点 O,交 AD 于点 N.易知△OGH为等腰直角三角形, 所以GH=1.
【解法四】如图4,连接FG并延长至点O,使OG=GF,连接BD,易知点 O 为正方形对角线的交点,GH 是△OFD 的中位线,所以
【解法五】如图5,建立如图所示的平面直角坐标系.易知E(0, ),C(2 ,0),F( ,0),D(2 ,2 所以
所以
【解法六】如图6,根据图形特性,将图形放在格点图中,小正方形的边长为 ,观察可得GH=1.
11.解析 (1)证明:∵ △ABO 是等边三角形,∴OA =OB=AB,∵四边形ABCD 是平行四边形,∴OA=OC,OB=OD,.. OA=OC=OB=OD,∴AC=BD,∴四边形ABCD 是矩形.
(2)∵ 四边形 ABCD 是矩形,.. ∠ABC=90°,AC=2AO,∵AB=1,∴AO=1,∴AC=2,由勾股定理得 ∴矩形 ABCD 的面积
12.解析 (1)四边形 BPCO 为平行四边形.
理由:∵四边形 ABCD 为平行四边形,∴OC=OA= ∵分别以点 B,C为圆心, AC, BD的长为半径画弧,两弧交于点 P,∴OB=CP,BP=OC,∴四边形 BPCO为平行四边形.
(2)当AC⊥BD,AC=BD时,四边形 BPCO 为正方形.·AC⊥BD,∴∠BOC=90°,.. BPCO为矩形. .矩形 BPCO 为正方形.
13.解析 (1)证明:如图 1,作 EM⊥BC 于 M,EN⊥CD于 N,易知四边形 EMCN 是矩形,
,、∠MEN=90°,
∵点 E 是正方形ABCD 对角线上的点,∴EM=EN,
∵∠DEF=90°,∴∠DEN=∠MEF=90°-∠FEN,在△DEN和△FEM中, ∴△DEN≌△FEM(ASA),∴ EF=DE,∴矩形 DEFG是正方形.
(2)∵ 四边形 DEFG和四边形ABCD 是正方形,.. DE = DG,AD= DC, . ∠CDG+∠CDE = ∠ADE+∠CDE=90°,..∠CDG=∠ADE,在△ADE和△CDG中,
.. △ADE≌△CDG(SAS),
.. AE=CG,∠DAE=∠DCG=45°,
··∠ACD=45°,∴∠ACG=∠ACD+∠DCG=90°,
.. CE⊥CG,.. CE+CG=CE+AE=AC= AB=9
如图2,连接EG,
,正方形 DEFG的边长为3
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
