2024-2025学年河北省保定市新秀学校七年级(下)月考数学试卷(3月份)(含答案)
文档属性
| 名称 | 2024-2025学年河北省保定市新秀学校七年级(下)月考数学试卷(3月份)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 82.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 16:16:42 | ||
图片预览


文档简介
2024-2025学年河北省保定市新秀学校七年级(下)月考数学试卷(3月份)
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.墨迹覆盖了等式“x3x=x2(x≠0)”中的运算符号,则覆盖的是( )
A. + B. - C. × D. ÷
2.下列能用平方差公式计算的是( )
A. (a-b)(-a+b) B. (2b-1)(-2a-1)
C. (a+b)(b-a) D. (2a+1)(-2a-1)
3.下列计算正确的是( )
A. (-5)0=0 B. x2+x3=x5 C. (ab2)3=a3b5 D. 2a2 a-1=2a
4.若k为正整数,则=( )
A. k2k B. k2 C. 2kk D. k
5.若x和y互为倒数,则(x+)(2y-)的值是( )
A. 1 B. 2 C. 3 D. 4
6.将9.52变形正确的是( )
A. 9.52=92+0.52 B. 9.52=(10+0.5)(10-0.5)
C. 9.52=102-2×10×0.5+0.52 D. 9.52=92+9×0.5+0.52
7.小明总结了以下结论:
①a(b+c)=ab+ac;
②a(b-c)=ab-ac;
③(b-c)÷a=b÷a-c÷a(a≠0);
④a÷(b+c)=a÷b+a÷c(a≠0)
其中一定成立的个数是( )
A. 1 B. 2 C. 3 D. 4
8.若将(2x+a)(2x-b)展开的结果中不含有x项,则a,b满足的关系式是( )
A. ab=1 B. ab=0 C. a-b=0 D. a+b=0
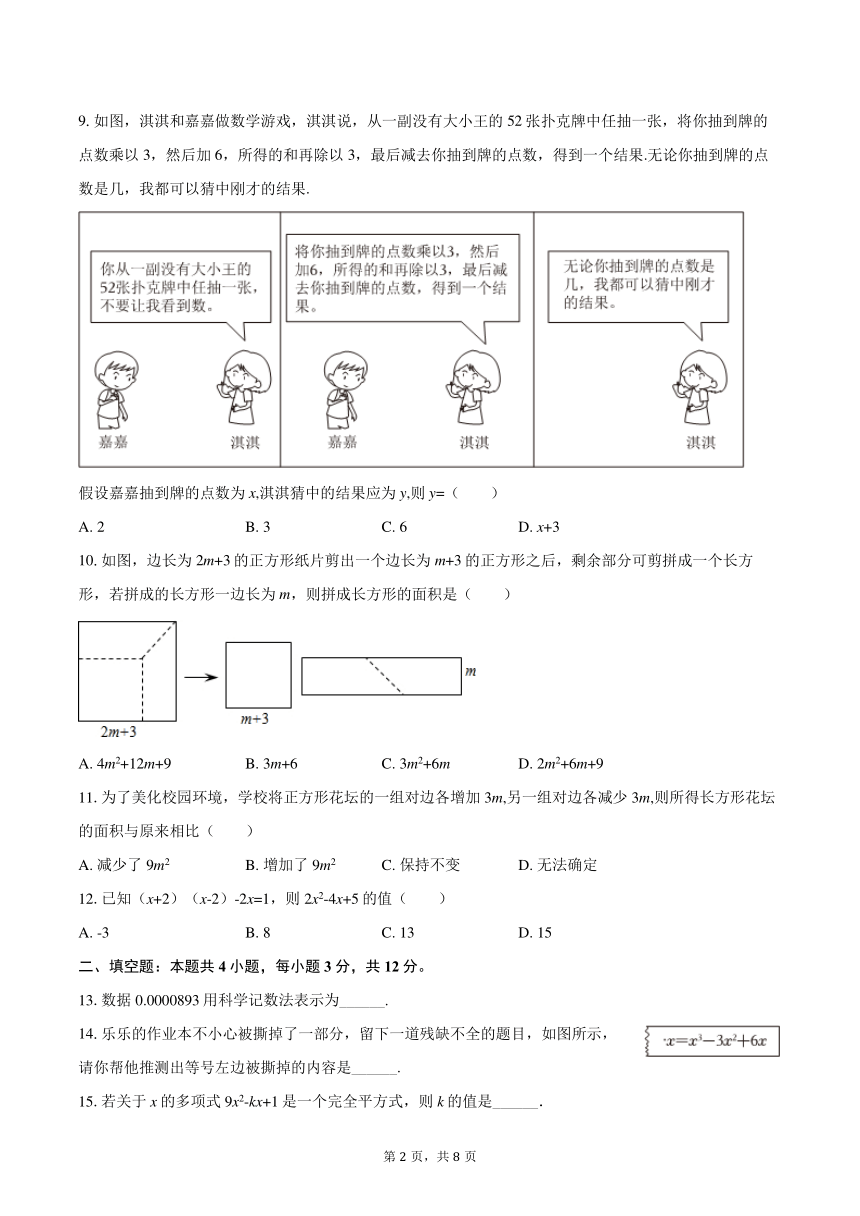
9.如图,淇淇和嘉嘉做数学游戏,淇淇说,从一副没有大小王的52张扑克牌中任抽一张,将你抽到牌的点数乘以3,然后加6,所得的和再除以3,最后减去你抽到牌的点数,得到一个结果.无论你抽到牌的点数是几,我都可以猜中刚才的结果.
假设嘉嘉抽到牌的点数为x,淇淇猜中的结果应为y,则y=( )
A. 2 B. 3 C. 6 D. x+3
10.如图,边长为2m+3的正方形纸片剪出一个边长为m+3的正方形之后,剩余部分可剪拼成一个长方形,若拼成的长方形一边长为m,则拼成长方形的面积是( )
A. 4m2+12m+9 B. 3m+6 C. 3m2+6m D. 2m2+6m+9
11.为了美化校园环境,学校将正方形花坛的一组对边各增加3m,另一组对边各减少3m,则所得长方形花坛的面积与原来相比( )
A. 减少了9m2 B. 增加了9m2 C. 保持不变 D. 无法确定
12.已知(x+2)(x-2)-2x=1,则2x2-4x+5的值( )
A. -3 B. 8 C. 13 D. 15
二、填空题:本题共4小题,每小题3分,共12分。
13.数据0.0000893用科学记数法表示为______.
14.乐乐的作业本不小心被撕掉了一部分,留下一道残缺不全的题目,如图所示,请你帮他推测出等号左边被撕掉的内容是______.
15.若关于x的多项式9x2-kx+1是一个完全平方式,则k的值是______.
16.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“幸运数”.如:4=22-02,12=42-22,20=62-42,28=82-62,因此4,12,20,28都可以称为“幸运数”.
(1)请判断:44______“幸运数”(填“是”或“不是”);
(2)设这两个连续偶数为2k+2和2k(其中k取非负整数),用k表示“幸运数是______.
三、解答题:本题共7小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题16分)
计算:
(1)(-2ab)3 (3b)2;
(2);
(3)(x+y+1)(x+y-1);
(4).
18.(本小题10分)
先化简,再求值:
(1)(2x+3y)2-(2x+y)(2x-y),其中,y=-1.
(2)[(2+ab)(2-ab)+3a2b2-4]÷ab,其中.
19.(本小题8分)
如图,一块长方形土地,长为(4a+b)米,宽为(a+2b)米,现准备在这块土地上修建一个长为(3a+b)米,宽为(a+b)米的花坛,剩余部分修建成休息区域.
(1)请用含a和b的代数式表示休息区域的面积(结果要化简);
(2)若x2+2x+23=(x-2)2+a(x+5)-b恒成立,求休息区域的面积.
20.(本小题7分)
现有甲,乙,丙三种不同的矩形纸片(边长如图).
(1)取甲,乙纸片各1块,其面积和为______.
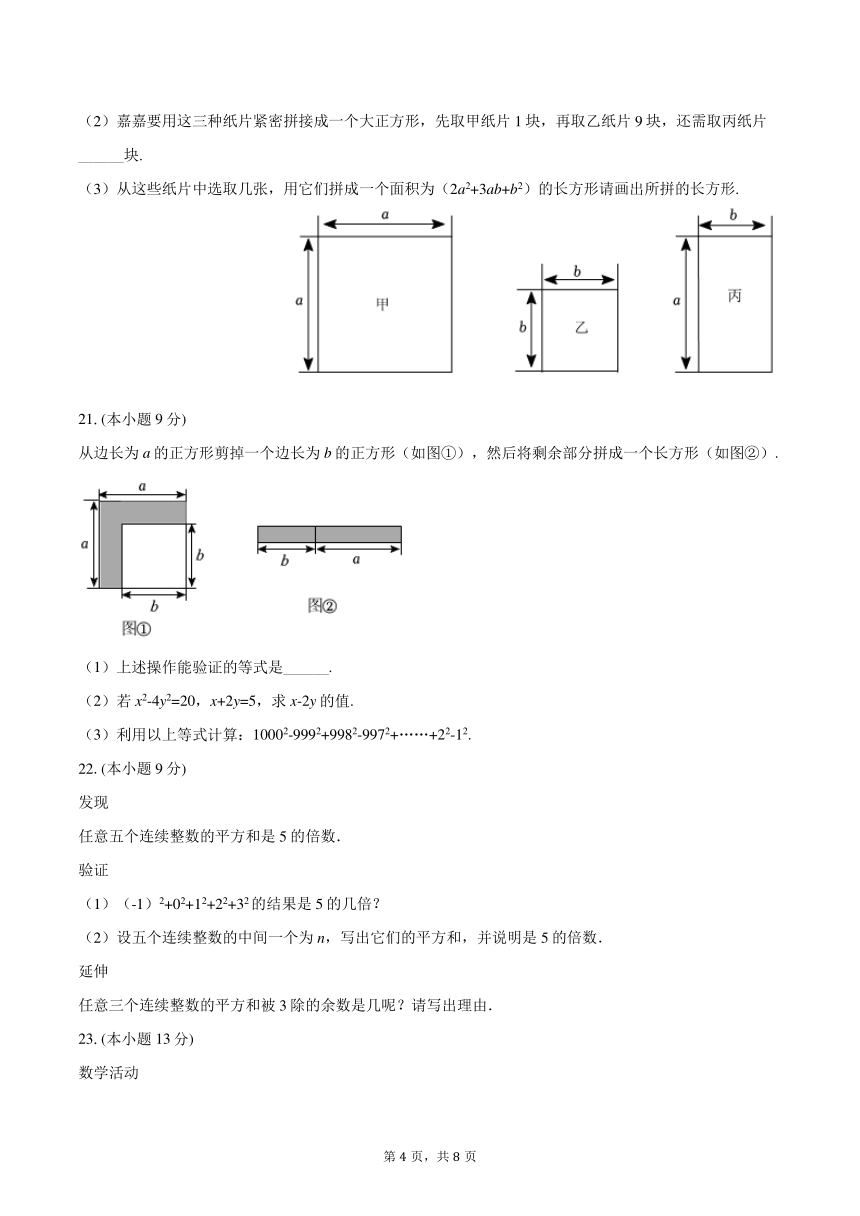
(2)嘉嘉要用这三种纸片紧密拼接成一个大正方形,先取甲纸片1块,再取乙纸片9块,还需取丙纸片______块.
(3)从这些纸片中选取几张,用它们拼成一个面积为(2a2+3ab+b2)的长方形请画出所拼的长方形.
21.(本小题9分)
从边长为a的正方形剪掉一个边长为b的正方形(如图①),然后将剩余部分拼成一个长方形(如图②).
(1)上述操作能验证的等式是______.
(2)若x2-4y2=20,x+2y=5,求x-2y的值.
(3)利用以上等式计算:10002-9992+9982-9972+……+22-12.
22.(本小题9分)
发现
任意五个连续整数的平方和是5的倍数.
验证
(1)(-1)2+02+12+22+32的结果是5的几倍?
(2)设五个连续整数的中间一个为n,写出它们的平方和,并说明是5的倍数.
延伸
任意三个连续整数的平方和被3除的余数是几呢?请写出理由.
23.(本小题13分)
数学活动
【知识生成】
数形结合是数学学习的一种重要的思想方法,借助图的直观性,可以帮助理解数学问题.
(1)如图1是一个边长为a+b的正方形,用两条分割线将其分为两个正方形和两个长方形,正方形的边长分别为a和b;图2是一个边长为a的正方形,用两条分割线将其分为两个正方形和两个长方形,正方形的边长分别为a-b和b,请分别写出阴影部分的面积所揭示的乘法公式:图1:______;图2:______.
【拓展探究】
(2)用4个全等的长和宽分别为a,b的长方形拼摆成一个如图3的正方形,请你直接写出阴影部分的面积所揭示的这三个代数式(a+b)2,(a-b)2,ab之间的等量关系,并通过运算验证它的正确性.
【解决问题】
(3)如图4,长方形ABCD周长为14cm,,求长方形ABCD的面积.
【知识迁移】
(4)若(2025-m)(2023-m)=12,则(2023-m)2+(2025-m)2=______.(直接写出结果)
1.【答案】D
2.【答案】C
3.【答案】D
4.【答案】A
5.【答案】B
6.【答案】C
7.【答案】C
8.【答案】C
9.【答案】A
10.【答案】C
11.【答案】A
12.【答案】D
13.【答案】8.93×10-5
14.【答案】x2-3x+6
15.【答案】±6
16.【答案】是; 4(2k+1).
17.【答案】-72a3b5;
-6 x+2y-1;
x2+2xy+y2-1;
-7.
18.【答案】12xy+10y2,4;
2 ab,-1.
19.【答案】解:(1)休息区域的面积为:(4a+b)(a+2b)-(3a+b)(a+b)
=4a2+8ab+ab+2b2-(3a2+3ab+ab+b2)
=4a2+9ab+2b2-3a2-4ab-b2
=a2+5ab+b2(平方米);
(2)x2+2x+23=(x-2)2+a(x+5)-b,
x2+2x+23=x2-4x+4+ax+5a-b,
x2+2x+23=x2+(a-4)x+4+5a-b,
∴a-4=2,4+5a-b=23,
解得a=6,b=11,
∴a2+5ab+b2
=62+5×6×11+112
=36+330+121
=487(平方米).
20.【答案】a2+b2;
6;
21.【答案】a2-b2=(a+b)(a-b); 4; 500500.
22.【答案】解:发现任意五个连续整数的平方和是5的倍数.
验证
(1)(-1)2+02+12+22+32=1+0+1+4+9=15,
15=5×3,
即(-1)2+02+12+22+32的结果是5的3倍;
(2)设五个连续整数的中间一个为n,则其余的4个整数分别是n-2,n-1,n+1,n+2,
它们的平方和为:(n-2)2+(n-1)2+n2+(n+1)2+(n+2)2
=n2-4n+4+n2-2n+1+n2+n2+2n+1+n2+4n+4
=5n2+10,
∵5n2+10=5(n2+2),n是整数,
∴n2+2是整数,
∴五个连续整数的平方和是5的倍数;
延伸
设三个连续整数的中间一个为n,则其余的2个整数是n-1,n+1,
它们的平方和为:(n-1)2+n2+(n+1)2
=n2-2n+1+n2+n2+2n+1
=3n2+2,
∵n是整数,
∴n2是整数,
∴任意三个连续整数的平方和被3除的余数是2.
23.【答案】(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2;
(a-b)2=(a+b)2-4ab,
验证:(a-b)2=a2-2ab+b2,
(a+b)2-4ab=a2+2ab+b2-4ab=a2-2ab+b2,
∴(a-b)2=(a+b)2-4ab;
10 cm2;
28.
第1页,共1页
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.墨迹覆盖了等式“x3x=x2(x≠0)”中的运算符号,则覆盖的是( )
A. + B. - C. × D. ÷
2.下列能用平方差公式计算的是( )
A. (a-b)(-a+b) B. (2b-1)(-2a-1)
C. (a+b)(b-a) D. (2a+1)(-2a-1)
3.下列计算正确的是( )
A. (-5)0=0 B. x2+x3=x5 C. (ab2)3=a3b5 D. 2a2 a-1=2a
4.若k为正整数,则=( )
A. k2k B. k2 C. 2kk D. k
5.若x和y互为倒数,则(x+)(2y-)的值是( )
A. 1 B. 2 C. 3 D. 4
6.将9.52变形正确的是( )
A. 9.52=92+0.52 B. 9.52=(10+0.5)(10-0.5)
C. 9.52=102-2×10×0.5+0.52 D. 9.52=92+9×0.5+0.52
7.小明总结了以下结论:
①a(b+c)=ab+ac;
②a(b-c)=ab-ac;
③(b-c)÷a=b÷a-c÷a(a≠0);
④a÷(b+c)=a÷b+a÷c(a≠0)
其中一定成立的个数是( )
A. 1 B. 2 C. 3 D. 4
8.若将(2x+a)(2x-b)展开的结果中不含有x项,则a,b满足的关系式是( )
A. ab=1 B. ab=0 C. a-b=0 D. a+b=0
9.如图,淇淇和嘉嘉做数学游戏,淇淇说,从一副没有大小王的52张扑克牌中任抽一张,将你抽到牌的点数乘以3,然后加6,所得的和再除以3,最后减去你抽到牌的点数,得到一个结果.无论你抽到牌的点数是几,我都可以猜中刚才的结果.
假设嘉嘉抽到牌的点数为x,淇淇猜中的结果应为y,则y=( )
A. 2 B. 3 C. 6 D. x+3
10.如图,边长为2m+3的正方形纸片剪出一个边长为m+3的正方形之后,剩余部分可剪拼成一个长方形,若拼成的长方形一边长为m,则拼成长方形的面积是( )
A. 4m2+12m+9 B. 3m+6 C. 3m2+6m D. 2m2+6m+9
11.为了美化校园环境,学校将正方形花坛的一组对边各增加3m,另一组对边各减少3m,则所得长方形花坛的面积与原来相比( )
A. 减少了9m2 B. 增加了9m2 C. 保持不变 D. 无法确定
12.已知(x+2)(x-2)-2x=1,则2x2-4x+5的值( )
A. -3 B. 8 C. 13 D. 15
二、填空题:本题共4小题,每小题3分,共12分。
13.数据0.0000893用科学记数法表示为______.
14.乐乐的作业本不小心被撕掉了一部分,留下一道残缺不全的题目,如图所示,请你帮他推测出等号左边被撕掉的内容是______.
15.若关于x的多项式9x2-kx+1是一个完全平方式,则k的值是______.
16.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“幸运数”.如:4=22-02,12=42-22,20=62-42,28=82-62,因此4,12,20,28都可以称为“幸运数”.
(1)请判断:44______“幸运数”(填“是”或“不是”);
(2)设这两个连续偶数为2k+2和2k(其中k取非负整数),用k表示“幸运数是______.
三、解答题:本题共7小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题16分)
计算:
(1)(-2ab)3 (3b)2;
(2);
(3)(x+y+1)(x+y-1);
(4).
18.(本小题10分)
先化简,再求值:
(1)(2x+3y)2-(2x+y)(2x-y),其中,y=-1.
(2)[(2+ab)(2-ab)+3a2b2-4]÷ab,其中.
19.(本小题8分)
如图,一块长方形土地,长为(4a+b)米,宽为(a+2b)米,现准备在这块土地上修建一个长为(3a+b)米,宽为(a+b)米的花坛,剩余部分修建成休息区域.
(1)请用含a和b的代数式表示休息区域的面积(结果要化简);
(2)若x2+2x+23=(x-2)2+a(x+5)-b恒成立,求休息区域的面积.
20.(本小题7分)
现有甲,乙,丙三种不同的矩形纸片(边长如图).
(1)取甲,乙纸片各1块,其面积和为______.
(2)嘉嘉要用这三种纸片紧密拼接成一个大正方形,先取甲纸片1块,再取乙纸片9块,还需取丙纸片______块.
(3)从这些纸片中选取几张,用它们拼成一个面积为(2a2+3ab+b2)的长方形请画出所拼的长方形.
21.(本小题9分)
从边长为a的正方形剪掉一个边长为b的正方形(如图①),然后将剩余部分拼成一个长方形(如图②).
(1)上述操作能验证的等式是______.
(2)若x2-4y2=20,x+2y=5,求x-2y的值.
(3)利用以上等式计算:10002-9992+9982-9972+……+22-12.
22.(本小题9分)
发现
任意五个连续整数的平方和是5的倍数.
验证
(1)(-1)2+02+12+22+32的结果是5的几倍?
(2)设五个连续整数的中间一个为n,写出它们的平方和,并说明是5的倍数.
延伸
任意三个连续整数的平方和被3除的余数是几呢?请写出理由.
23.(本小题13分)
数学活动
【知识生成】
数形结合是数学学习的一种重要的思想方法,借助图的直观性,可以帮助理解数学问题.
(1)如图1是一个边长为a+b的正方形,用两条分割线将其分为两个正方形和两个长方形,正方形的边长分别为a和b;图2是一个边长为a的正方形,用两条分割线将其分为两个正方形和两个长方形,正方形的边长分别为a-b和b,请分别写出阴影部分的面积所揭示的乘法公式:图1:______;图2:______.
【拓展探究】
(2)用4个全等的长和宽分别为a,b的长方形拼摆成一个如图3的正方形,请你直接写出阴影部分的面积所揭示的这三个代数式(a+b)2,(a-b)2,ab之间的等量关系,并通过运算验证它的正确性.
【解决问题】
(3)如图4,长方形ABCD周长为14cm,,求长方形ABCD的面积.
【知识迁移】
(4)若(2025-m)(2023-m)=12,则(2023-m)2+(2025-m)2=______.(直接写出结果)
1.【答案】D
2.【答案】C
3.【答案】D
4.【答案】A
5.【答案】B
6.【答案】C
7.【答案】C
8.【答案】C
9.【答案】A
10.【答案】C
11.【答案】A
12.【答案】D
13.【答案】8.93×10-5
14.【答案】x2-3x+6
15.【答案】±6
16.【答案】是; 4(2k+1).
17.【答案】-72a3b5;
-6 x+2y-1;
x2+2xy+y2-1;
-7.
18.【答案】12xy+10y2,4;
2 ab,-1.
19.【答案】解:(1)休息区域的面积为:(4a+b)(a+2b)-(3a+b)(a+b)
=4a2+8ab+ab+2b2-(3a2+3ab+ab+b2)
=4a2+9ab+2b2-3a2-4ab-b2
=a2+5ab+b2(平方米);
(2)x2+2x+23=(x-2)2+a(x+5)-b,
x2+2x+23=x2-4x+4+ax+5a-b,
x2+2x+23=x2+(a-4)x+4+5a-b,
∴a-4=2,4+5a-b=23,
解得a=6,b=11,
∴a2+5ab+b2
=62+5×6×11+112
=36+330+121
=487(平方米).
20.【答案】a2+b2;
6;
21.【答案】a2-b2=(a+b)(a-b); 4; 500500.
22.【答案】解:发现任意五个连续整数的平方和是5的倍数.
验证
(1)(-1)2+02+12+22+32=1+0+1+4+9=15,
15=5×3,
即(-1)2+02+12+22+32的结果是5的3倍;
(2)设五个连续整数的中间一个为n,则其余的4个整数分别是n-2,n-1,n+1,n+2,
它们的平方和为:(n-2)2+(n-1)2+n2+(n+1)2+(n+2)2
=n2-4n+4+n2-2n+1+n2+n2+2n+1+n2+4n+4
=5n2+10,
∵5n2+10=5(n2+2),n是整数,
∴n2+2是整数,
∴五个连续整数的平方和是5的倍数;
延伸
设三个连续整数的中间一个为n,则其余的2个整数是n-1,n+1,
它们的平方和为:(n-1)2+n2+(n+1)2
=n2-2n+1+n2+n2+2n+1
=3n2+2,
∵n是整数,
∴n2是整数,
∴任意三个连续整数的平方和被3除的余数是2.
23.【答案】(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2;
(a-b)2=(a+b)2-4ab,
验证:(a-b)2=a2-2ab+b2,
(a+b)2-4ab=a2+2ab+b2-4ab=a2-2ab+b2,
∴(a-b)2=(a+b)2-4ab;
10 cm2;
28.
第1页,共1页
同课章节目录
