23.1 图形的旋转第2课时 旋转作图 课件(共22张PPT) 2025-2026学年度人教版数学九年级上册
文档属性
| 名称 | 23.1 图形的旋转第2课时 旋转作图 课件(共22张PPT) 2025-2026学年度人教版数学九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 06:51:50 | ||
图片预览

文档简介
(共22张PPT)
23.1 图形的旋转
第二十三章 旋转
第2课时 旋转作图
A
B
C
D
E
F
G
H
K
L
M
N
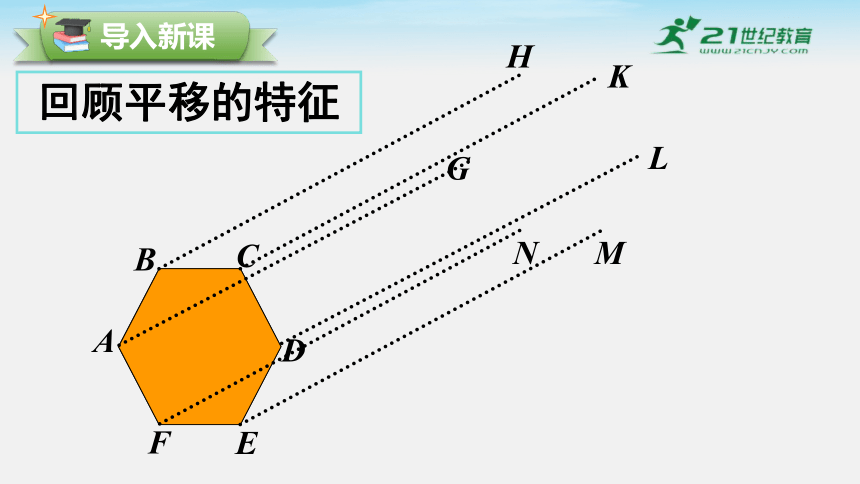
回顾平移的特征
O
E
︵
A
C
B
D
F
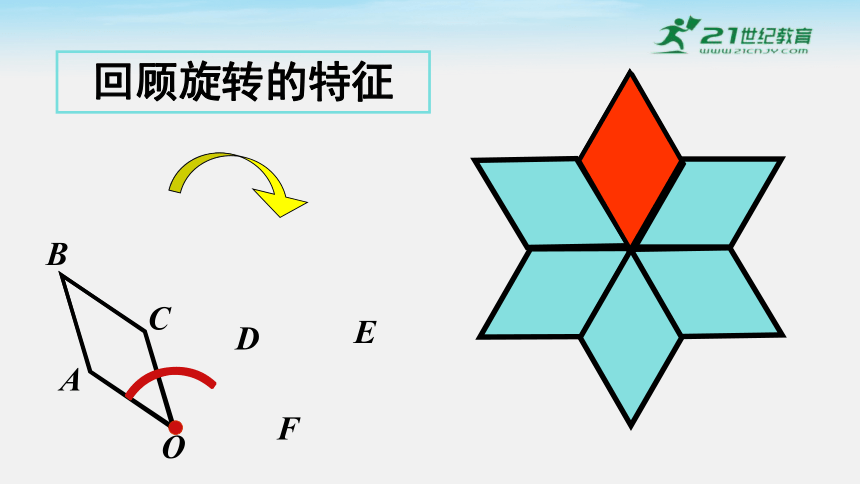
回顾旋转的特征
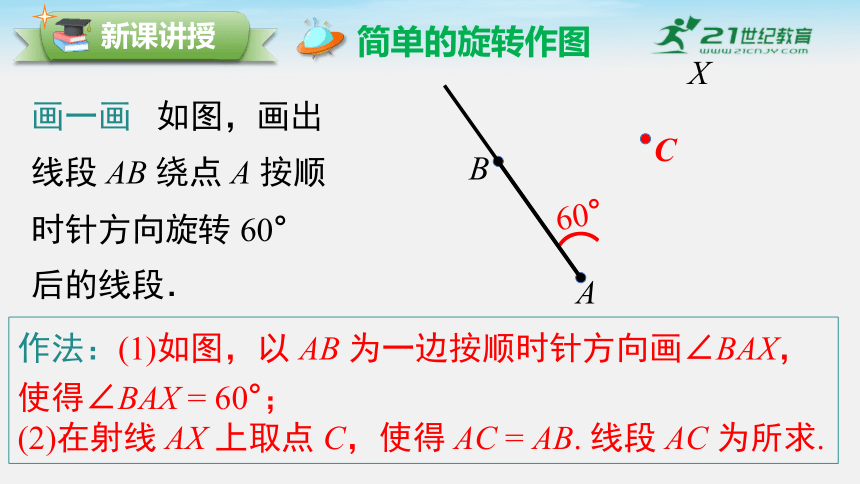
画一画 如图,画出
线段 AB 绕点 A 按顺
时针方向旋转 60°
后的线段.
简单的旋转作图
作法:(1)如图,以 AB 为一边按顺时针方向画∠BAX,使得∠BAX = 60°;
(2)在射线 AX 上取点 C,使得 AC = AB. 线段 AC 为所求.
X
︵
60°
A
B
C
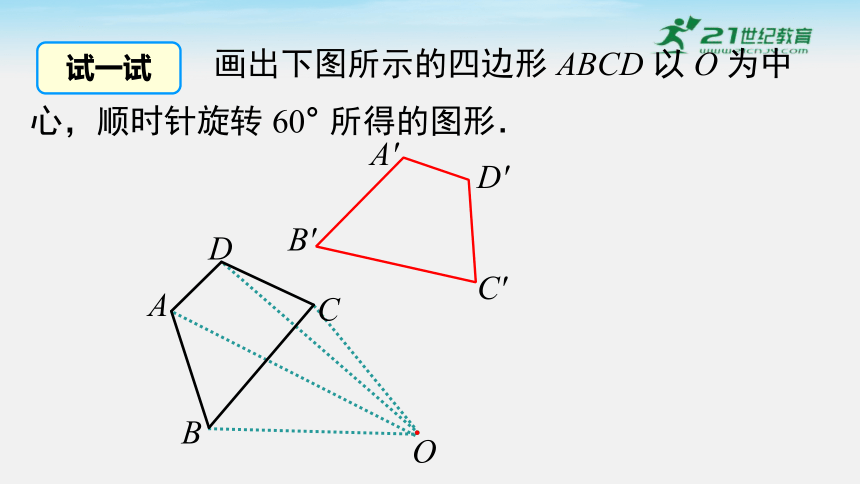
画出下图所示的四边形 ABCD 以 O 为中心,顺时针旋转 60° 所得的图形.
试一试
B'
A'
C'
D'
A
B
C
D
O
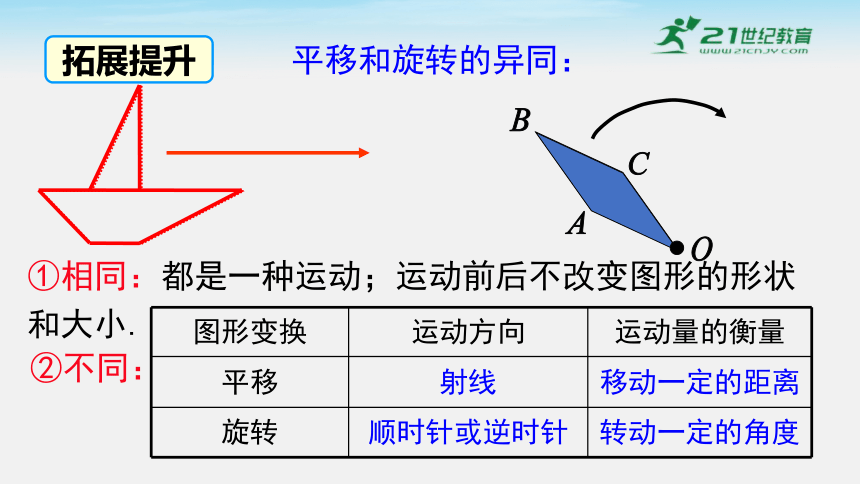
拓展提升
①相同:都是一种运动;运动前后不改变图形的形状和大小.
A
②不同:
图形变换 运动方向 运动量的衡量
平移 射线 移动一定的距离
旋转 顺时针或逆时针 转动一定的角度
平移和旋转的异同:
O
C
B
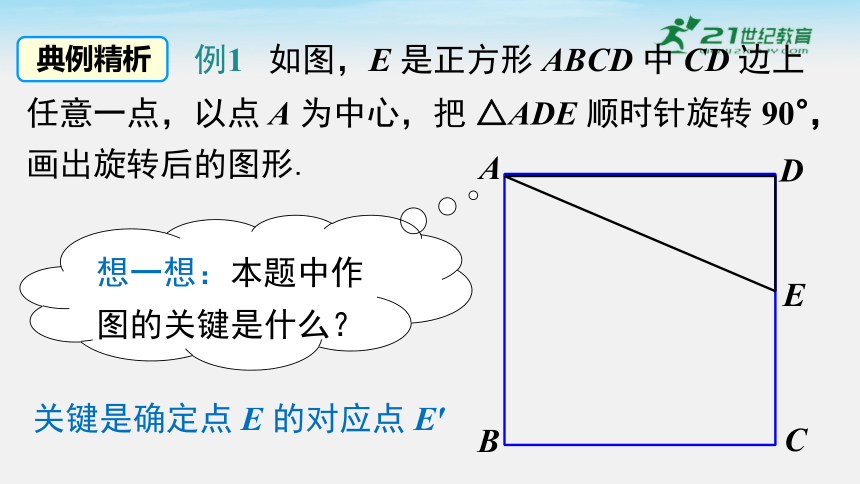
例1 如图,E 是正方形 ABCD 中 CD 边上任意一点,以点 A 为中心,把 △ADE 顺时针旋转 90°,画出旋转后的图形.
关键是确定点 E 的对应点 E′
想一想:本题中作图的关键是什么?
典例精析
A
B
C
D
E
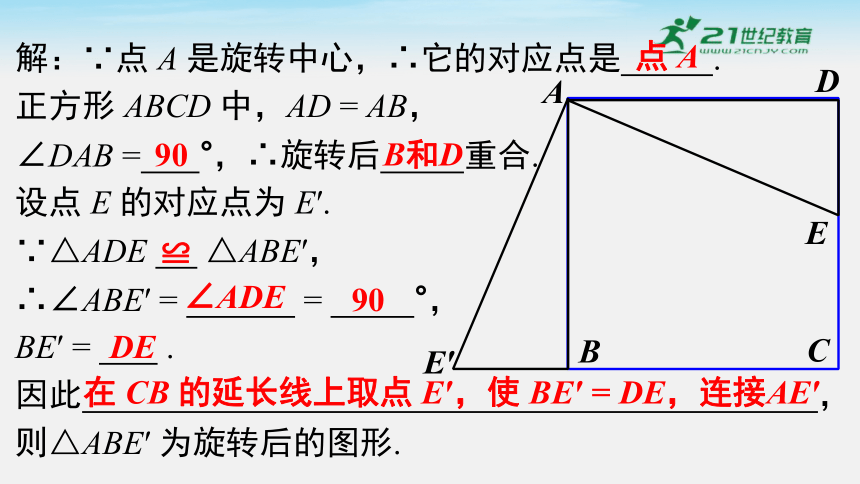
解:∵点 A 是旋转中心,∴它的对应点是 .
正方形 ABCD 中,AD = AB,
∠DAB = °,∴旋转后 重合.
设点 E 的对应点为 E′.
∵△ADE △ABE′,
∴∠ABE′ = = °,
BE′ = .
因此 ,
A
B
C
D
E
E′
点 A
90
≌
∠ADE
90
DE
在 CB 的延长线上取点 E′,使 BE′ = DE,连接AE′
则△ABE′ 为旋转后的图形.
B和D
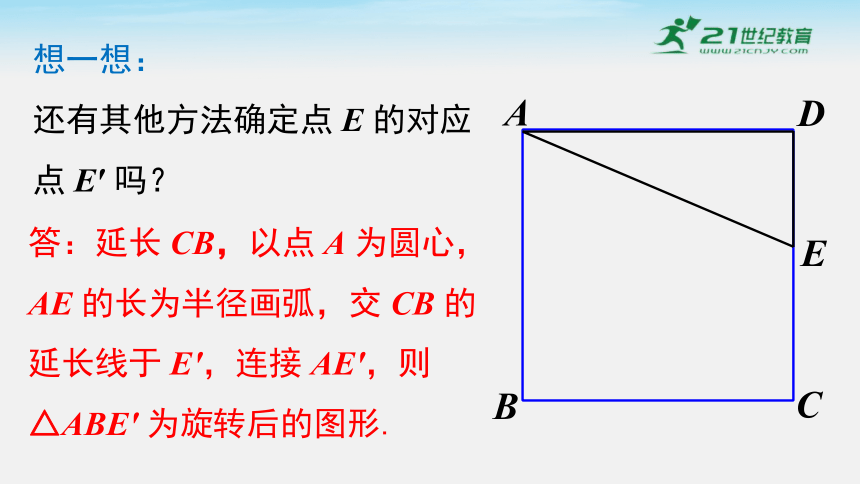
答:延长 CB,以点 A 为圆心,AE 的长为半径画弧,交 CB 的延长线于 E',连接 AE',则△ABE' 为旋转后的图形.
A
B
C
D
E
想一想:
还有其他方法确定点 E 的对应点 E′ 吗?
(1) 明确旋转三要素:
旋转中心、旋转方向和旋转角度.
旋转作图的基本步骤:
方法归纳
(2) 找出关键点;
(3) 作出关键点的对应点;
(4) 作出新图形;
(5) 写出结论.
A
B
O
练一练 下图为 4×4 的正方形网格,每个小正方形的边长均为 1,将 △OAB 绕点 O 逆时针旋转 90°,你能画出
△OAB 旋转后的图形△OA′B′ 吗?
A′
B′
例2 如图,点 A,C 的坐标分别为 (1,1),(2,4),将△ABC 绕点 A 按逆时针方向旋转 90°,得到△AB'C',则点 C 的对应点 C' 的坐标为( )
A.(-2,4) B.(4,0)
C.(-2,2) D.(-1,3)
C
分析:根据题意画出图形,然后结合直角坐标系即可得出 C' 的坐标.
练一练 如图,正方形 OABC 的两边 OA、OC 分别在 x 轴、y 轴上,点 D(5,3) 在边 AB 上,以 C 为中心,把△CDB 旋转 90°,则旋转后点 D 的对应点 D′ 的坐标是( )
A. (2,10) B. (-2,0)
C. (2,10) 或(-2,0)
D. (10,2) 或(-2,0)
分析:要注意分顺时针旋转和逆时针旋转两种情况讨论.
C
方法点拨:关于平面直角坐标系中的图形旋转后对应点的坐标的计算,通常要结合已知点及其对应点构造直角三角形,利用旋转的性质,证明所构造的两个直角三角形全等即可解决.
旋转设计作图
1.选择不同的_________、不同的_______旋转同一个图案,会出现不同的效果.
(1)两个旋转中,旋转中心不变,_______改变了,产生了_______的旋转效果.
(2)两个旋转中,旋转角不变,__________改变了,产生了_______的旋转效果.
旋转中心
旋转角
旋转角
不同
旋转中心
不同
合作探究
α
o
o
2. 我们可以借助旋转可以设计出许多美丽的图案.
例3 如图,该图形在绕中心点 O 按下列角度旋转后,不能与其自身重合的是( )
A.72°
B.108°
C.144°
D.216°
B
1. 如图,是由一个矩形沿顺时针方向旋转 90° 后所形成的图形是( )
A. (1)(3) B. (2)(3)
C. (1)(2) D. (3)
2. 等边三角形绕着它的中心 O 旋转,若旋转后的三角形能与自身重合,则旋转角最小是( )
A.360° B.240° C.120° D.60°
B
C
3. 如图,在平面直角坐标系中,已知△ABC 的顶点 A 的坐标为(-1,2).
(1)将△ABC 向右平移 3 个单位得到△DEF,
请在图中画出平移后的图形;
(2)将△ABC 绕点 C 按逆时针方
向旋转 90° 后得到△MNC,请在
图中画出旋转后的图形,并写出
点 M,N 的坐标.
解:(1)如图,△DEF 为所作.
(2)如图,△MNC 为所作,M(-3,-2),N(-2,-4).
4. 如图,四边形 ABCD 绕 O 点旋转后,顶点 A 的对应点为 E,试确定 B、C、D 对应的点的位置,以及旋转后的四边形.
解:(1)连接 OA、OB、OC、OD、OE;
(2)分别以 OB、OC、OD 为一边作∠BOF,∠COG, ∠DOH,使∠BOF = ∠COG = ∠DOH = ∠AOE;
(3)分别在射线 OF,OG,OH 上,截取 OF = OB,OG = OC,OH = OD;
(4)连接 EF,FG,GH,HE.
四边形 EFGH 就是四边形 ABCD 绕 O 点旋转后的图形.
旋转作图
作旋转图形
①分析图形,找出图形的关键点;
②确定三要素;
③将关键点分别与旋转中心连接后旋转,找到关键点的对应点;
④顺次连接各对应点
设计图案
利用旋转和平移可以设计设计出美丽的图案
23.1 图形的旋转
第二十三章 旋转
第2课时 旋转作图
A
B
C
D
E
F
G
H
K
L
M
N
回顾平移的特征
O
E
︵
A
C
B
D
F
回顾旋转的特征
画一画 如图,画出
线段 AB 绕点 A 按顺
时针方向旋转 60°
后的线段.
简单的旋转作图
作法:(1)如图,以 AB 为一边按顺时针方向画∠BAX,使得∠BAX = 60°;
(2)在射线 AX 上取点 C,使得 AC = AB. 线段 AC 为所求.
X
︵
60°
A
B
C
画出下图所示的四边形 ABCD 以 O 为中心,顺时针旋转 60° 所得的图形.
试一试
B'
A'
C'
D'
A
B
C
D
O
拓展提升
①相同:都是一种运动;运动前后不改变图形的形状和大小.
A
②不同:
图形变换 运动方向 运动量的衡量
平移 射线 移动一定的距离
旋转 顺时针或逆时针 转动一定的角度
平移和旋转的异同:
O
C
B
例1 如图,E 是正方形 ABCD 中 CD 边上任意一点,以点 A 为中心,把 △ADE 顺时针旋转 90°,画出旋转后的图形.
关键是确定点 E 的对应点 E′
想一想:本题中作图的关键是什么?
典例精析
A
B
C
D
E
解:∵点 A 是旋转中心,∴它的对应点是 .
正方形 ABCD 中,AD = AB,
∠DAB = °,∴旋转后 重合.
设点 E 的对应点为 E′.
∵△ADE △ABE′,
∴∠ABE′ = = °,
BE′ = .
因此 ,
A
B
C
D
E
E′
点 A
90
≌
∠ADE
90
DE
在 CB 的延长线上取点 E′,使 BE′ = DE,连接AE′
则△ABE′ 为旋转后的图形.
B和D
答:延长 CB,以点 A 为圆心,AE 的长为半径画弧,交 CB 的延长线于 E',连接 AE',则△ABE' 为旋转后的图形.
A
B
C
D
E
想一想:
还有其他方法确定点 E 的对应点 E′ 吗?
(1) 明确旋转三要素:
旋转中心、旋转方向和旋转角度.
旋转作图的基本步骤:
方法归纳
(2) 找出关键点;
(3) 作出关键点的对应点;
(4) 作出新图形;
(5) 写出结论.
A
B
O
练一练 下图为 4×4 的正方形网格,每个小正方形的边长均为 1,将 △OAB 绕点 O 逆时针旋转 90°,你能画出
△OAB 旋转后的图形△OA′B′ 吗?
A′
B′
例2 如图,点 A,C 的坐标分别为 (1,1),(2,4),将△ABC 绕点 A 按逆时针方向旋转 90°,得到△AB'C',则点 C 的对应点 C' 的坐标为( )
A.(-2,4) B.(4,0)
C.(-2,2) D.(-1,3)
C
分析:根据题意画出图形,然后结合直角坐标系即可得出 C' 的坐标.
练一练 如图,正方形 OABC 的两边 OA、OC 分别在 x 轴、y 轴上,点 D(5,3) 在边 AB 上,以 C 为中心,把△CDB 旋转 90°,则旋转后点 D 的对应点 D′ 的坐标是( )
A. (2,10) B. (-2,0)
C. (2,10) 或(-2,0)
D. (10,2) 或(-2,0)
分析:要注意分顺时针旋转和逆时针旋转两种情况讨论.
C
方法点拨:关于平面直角坐标系中的图形旋转后对应点的坐标的计算,通常要结合已知点及其对应点构造直角三角形,利用旋转的性质,证明所构造的两个直角三角形全等即可解决.
旋转设计作图
1.选择不同的_________、不同的_______旋转同一个图案,会出现不同的效果.
(1)两个旋转中,旋转中心不变,_______改变了,产生了_______的旋转效果.
(2)两个旋转中,旋转角不变,__________改变了,产生了_______的旋转效果.
旋转中心
旋转角
旋转角
不同
旋转中心
不同
合作探究
α
o
o
2. 我们可以借助旋转可以设计出许多美丽的图案.
例3 如图,该图形在绕中心点 O 按下列角度旋转后,不能与其自身重合的是( )
A.72°
B.108°
C.144°
D.216°
B
1. 如图,是由一个矩形沿顺时针方向旋转 90° 后所形成的图形是( )
A. (1)(3) B. (2)(3)
C. (1)(2) D. (3)
2. 等边三角形绕着它的中心 O 旋转,若旋转后的三角形能与自身重合,则旋转角最小是( )
A.360° B.240° C.120° D.60°
B
C
3. 如图,在平面直角坐标系中,已知△ABC 的顶点 A 的坐标为(-1,2).
(1)将△ABC 向右平移 3 个单位得到△DEF,
请在图中画出平移后的图形;
(2)将△ABC 绕点 C 按逆时针方
向旋转 90° 后得到△MNC,请在
图中画出旋转后的图形,并写出
点 M,N 的坐标.
解:(1)如图,△DEF 为所作.
(2)如图,△MNC 为所作,M(-3,-2),N(-2,-4).
4. 如图,四边形 ABCD 绕 O 点旋转后,顶点 A 的对应点为 E,试确定 B、C、D 对应的点的位置,以及旋转后的四边形.
解:(1)连接 OA、OB、OC、OD、OE;
(2)分别以 OB、OC、OD 为一边作∠BOF,∠COG, ∠DOH,使∠BOF = ∠COG = ∠DOH = ∠AOE;
(3)分别在射线 OF,OG,OH 上,截取 OF = OB,OG = OC,OH = OD;
(4)连接 EF,FG,GH,HE.
四边形 EFGH 就是四边形 ABCD 绕 O 点旋转后的图形.
旋转作图
作旋转图形
①分析图形,找出图形的关键点;
②确定三要素;
③将关键点分别与旋转中心连接后旋转,找到关键点的对应点;
④顺次连接各对应点
设计图案
利用旋转和平移可以设计设计出美丽的图案
同课章节目录
