七年级上册数学期末考试押题卷(含解析)华东师大版2025—2026学年
文档属性
| 名称 | 七年级上册数学期末考试押题卷(含解析)华东师大版2025—2026学年 |  | |
| 格式 | docx | ||
| 文件大小 | 715.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 09:05:56 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
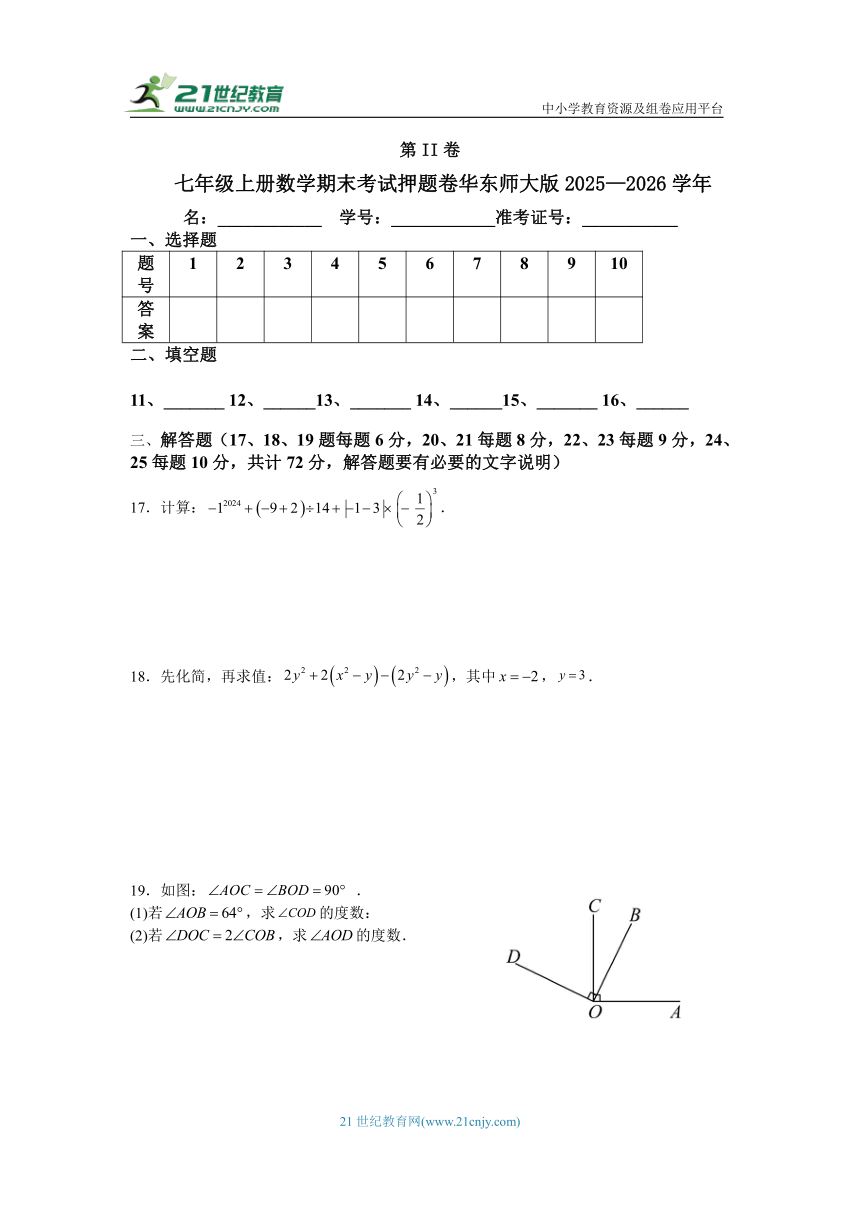
七年级上册数学期末考试押题卷华东师大版2025—2026学年
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.如果将作为标准身高,低于标准身高记作,那么身高应记作( )
A. B. C. D.
2.在同一平面内,若,,则的度数是( )
A.15° B.105° C.25°或105° D.15°或105°
3.的相反数是( )
A.2025 B. C. D.
4.已知单项式与的和仍是单项式,则( )
A.6 B.5 C.4 D.3
5.如图,已知直线,平分,若,则的度数为( )
A. B. C. D.
6.如果代数式的值是,则代数式的值是( )
A. B.4 C. D.2
7.如果,那么是( )
A.正数 B.负数 C.非正数 D.非负数
8.如图是某种细胞分裂示意图,这种细胞经过 1 次分裂便由 1 个分裂成 2 个.根据此规律,一个细胞经过 5 次分裂后可分裂成( )个细胞
A.10 B.16 C.32 D.64
9.如图,线段,动点P从A出发,以的速度沿运动,M为的中点,N为的中点.以下说法正确的是( )
①运动后,;
②的值随着运动时间的改变而改变;
③的值不变;
④当时,运动时间为.
A.①② B.②③ C.①②③ D.②③④
10.如图,直线,相交于点,,,平分,给出下列结论:①当时,;②为的平分线;③与相等的角有3个;④.其中正确的结论为()
A.①②④ B.②③④ C.①③④ D.①②③④
二、填空题(6小题,每题3分,共18分)
11.把数精确到百分位后的近似数是 .
12.的系数是 .
13.如图所示,AD∥BC,BD平分∠ABC,若∠A=110°,则∠D= .
14.若∠A=50°,则∠A的补角为 .
15.在数轴上,点A表示的数是5,若点B与点A之间距离是8,则点B表示的数是 .
16.如果整式A与整式的和为实数,我们称A,为的“友好整式”,例如:与为1的“友好整式”;与为7的“友好整式”.若关于的整式与为的“友好整式”,则的值为 .
第II卷
七年级上册数学期末考试押题卷华东师大版2025—2026学年
名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:.
18.先化简,再求值:,其中,.
19.如图: .
(1)若,求的度数:
(2)若,求的度数.
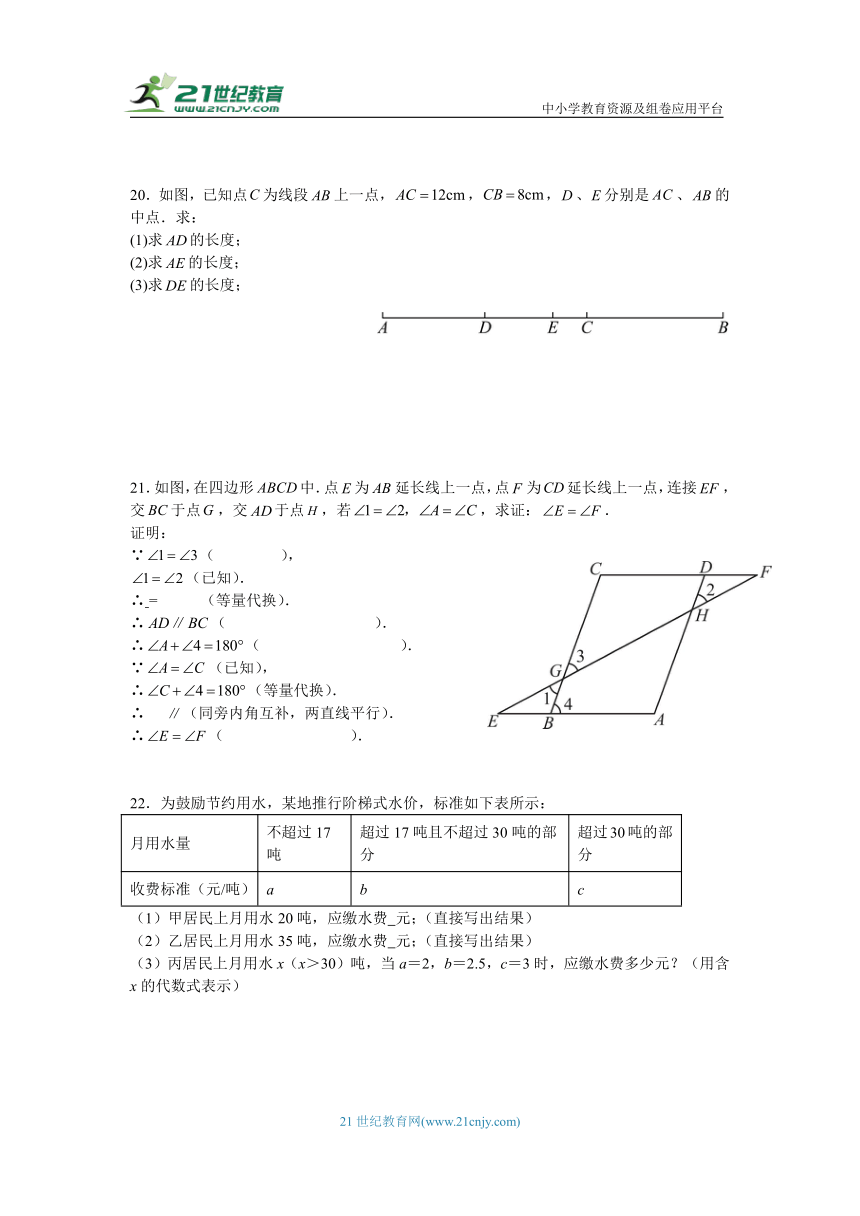
20.如图,已知点为线段上一点,,,、分别是、的中点.求:
(1)求的长度;
(2)求的长度;
(3)求的长度;
21.如图,在四边形中.点为延长线上一点,点为延长线上一点,连接,交于点,交于点,若,求证:.
证明:
∵( ),
(已知).
∴ = (等量代换).
∴( ).
∴( ).
∵(已知),
∴(等量代换).
∴ (同旁内角互补,两直线平行).
∴( ).
22.为鼓励节约用水,某地推行阶梯式水价,标准如下表所示:
月用水量 不超过17吨 超过17吨且不超过30吨的部分 超过30吨的部分
收费标准(元/吨) a b c
(1)甲居民上月用水20吨,应缴水费 元;(直接写出结果)
(2)乙居民上月用水35吨,应缴水费 元;(直接写出结果)
(3)丙居民上月用水x(x>30)吨,当a=2,b=2.5,c=3时,应缴水费多少元?(用含x的代数式表示)
23.由几个相同的、棱长为2的小立方块搭成的几何体如图所示,将它摆放在桌面上.
(1)画出这个几何体的三视图;
(2)求出这个几何体的表面积.
24.已知射线平分,点C为上任意一点,过点C作直线交射线于点D.
(1)如图1,若,则_________°;
(2)点E是射线上一动点(不与点C,D重合),平分交于点F,过点F作交于点G.
①如图2,若,当时,求的度数;
②当点E在运动过程中,设,,直接写出和之间的数量关系.
25.如图1,、两点在数轴上对应的数分别为和6.
(1)直接写出、两点之间的距离___;
(2)若在数轴上存在一点,使得,求点表示的数;
(3)如图2,现有动点、,若点从点出发,以每秒4个单位长度的速度沿数轴向右运动,同时点从点出发,以每秒2个单位长度的速度沿数轴向左运动,当点到达原点后立即以每秒3个单位长度的速度沿数轴向右运动,求:当时的运动时间的值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A C A B C C D C
二、填空题
11.
【分析】根据四舍五入法将题目中的数据精确到百分位即可.
【详解】解:把数精确到百分位后的近似数是,
故答案为:.
12.
【分析】本题主要考查了单项式的系数的定义,单项式中数字因数叫做这个单项式的系数,据此可得答案.
【详解】解:的系数是,
故答案为:.
13.35°/35度
【分析】根据平行线的性质先求得∠ABC的度数,再根据角平分线的性质及平行线的性质求得∠D的度数.
【详解】∵AD∥BC,∠A=110°,
∴∠ABC=180-∠A=70°;
又∵BD平分∠ABC,
∴∠DBC=35°;
∵AD∥BC,
∴∠D=∠DBC=35°.
故答案为35°.
14.130°
【分析】根据互为补角的两个角的和等于180°列式计算即可得解.
【详解】∠A的补角=180°﹣∠A=180°﹣50°=130°.
故答案为:130°.
15.-3或13
【分析】根据数轴上到一点距离相等的点有两个,分别位于该点的左右,可得答案.
【详解】在数轴上,点A表示数5,点B到点A的距离为8,则点B表示的数是 3或13.
故答案为 3或13.
16.7
【分析】本题主要考查整式的加减运算,掌握整式的加减运算法则成为解题的关键.
根据“友好整式”的定义可知的值与x无关,从而可求出k和n的值即可.
【详解】解:由题意可知:
,
令,得,
∴.
故答案为:7.
三、解答题
17.
【分析】本题考查了有理数的混合运算,绝对值的化简,熟悉掌握运算法则是解题的关键.
先运算乘方运算和化简绝对值,再运算乘除,最后运算加减即可.
【详解】解:
.
18.,
【分析】本题主要考查整式的化简,先去括号,然后合并同类项,最后把,的值代入即可.
【详解】解:
,
当,时,原式.
19.(1)
(2)
【分析】本题考查互余的定义,几何图形中角度的计算,熟练掌握各个角之间的互余和数量关系是解决问题的关键.
(1)根据,结合图形即可求出结论;
(2)根据,结合题意得出各个角度,再根据即可得出结论.
【详解】(1)解:,
由可得,
,
;
(2)解:由(1)知,
,,
,解得,
∴,,
.
20.(1)
(2)
(3)
【分析】本题考查了关于线段的中点的计算,线段的和与差的计算,读懂题意熟练运用线段的和差倍分是解本题的关键.
(1)直接根据是的中点可得答案;
(2)先求出的长,然后根据E是的中点求出,
(3)根据即可求出.
【详解】(1)解:∵,点D是的中点,
∴;
(2)∵,,
∴,
∵E是的中点,
∴,
(3)∵,
∴.
21.对顶角相等;;同位角相等,两直线平行;两直线平行,同旁内角互补;;两直线平行,内错角相等
【分析】运用平行线的判定与性质进行求解即可得出答案.
【详解】证明:∵(对顶角相等),
(已知),
∴(等量代换),
∴(同位角相等,两直线平行),
∴(两直线平行,同旁内角互补),
∵(已知),
∴(等量代换),
∴(同旁内角互补,两直线平行),
∴(两直线平行,内错角相等),
故答案为:对顶角相等;;同位角相等,两直线平行;两直线平行,同旁内角互补;;两直线平行,内错角相等.
22.(1)17a+3b(2)17a+13b+5c(3)3x-23.5
【分析】(1)上月用水20吨,则按照分为两部分,17吨部分和超过17吨的3吨部分,分别计算费用再求和.
(2)上月用水35吨,则按照三部分,17吨部分与30-17=13吨部分与35-30=5吨部分,分别计算费用在求和.
(3)根据(2)得出的代数式,把a,b,c的值代入即可得到.
【详解】(1)20<30,则分两部分,17吨部分价格为17a,超过17吨且不超过30吨的部分价格为(20-17)×b=3b.即应缴税费为17a+3b(元)
(2)35>30,则分为三部分,17吨部分价格为17a,超过17吨且不超过30吨的部分价格为(30-17)×b=13b,超过30吨的部分价格为(35-30)×c=5c.即应缴水费为17a+13b+5c(元)
(3)由(2)知,水量大于30吨时,水费为17a+13b+(x-30)c,把a=2,b=2.5,c=3代入得到,17a+13b+5c=17×2+13×2.5+(x-30)×3=3x-23.5(元)
23.(1)见解析
(2)88
【分析】本题考查了三视图的画法以及表面积的求法.主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,物体的表面积是指露在外部的所有表面积之和.
(1)分别画出从正面,上面,左面看到的图形即可;
(2)根据三视图求解六个面的面积和即可.
【详解】(1)解:画图如下:
;
(2)解:;
24.(1)60
(2)①;②或
【分析】本题考查平行线的性质,三角形内角和定理,也考查了角平分线的定义.
(1)根据角平分线的定义和平行线的性质即可求解;
(2)①由三角形内角和定理可得,由平行线的性质和角平分线的定义可得,,根据即可求解;②分为点在线段上和点在下方两种情况讨论,结合平行线的性质和角平分线的定义即可求解.
【详解】(1)解:∵,,
∴,
∵平分,
∴,
∴;
(2)解:①∵,,
∴,
∵,
∴,
∵平分,
∴,
∴,
∵平分,
∴,
∵,
∴;
②如图,点在线段上,
∵,
∴,
∵平分,平分,
∴,,
∵,
∴
,
∴,
如图,点在下方,
∵,
∴,
∵平分,平分,
∴,,
∵,
∴
,
即.
25.(1)22
(2)或
(3)当时的运动时间的值为2或秒
【分析】(1)根据两点间的距离公式即可求出、两点之间的距离;
(2)设点表示的数为.分两种情况:①点在线段上;②点在线段的延长线上.根据列出关于的方程,求解即可;
(3)根据点的运动方向分两种情况:①当时,点从点出发,以每秒2个单位长度的速度沿数轴向左运动;②当时,点从原点开始以每秒3个单位长度的速度沿数轴向右运动,根据列出关于的方程,解方程即可.
【详解】(1)解:、两点之间的距离是:;
(2)解:设点表示的数为.分两种情况:
①当点在线段上时,
,
,
解得;
②当点在线段的延长线上时,
,
,
解得.
综上所述,点表示的数为或;
(3)解:分两种情况:
①当时,点从点出发,以每秒2个单位长度的速度沿数轴向左运动,
此时点表示的数为,点表示的数为,
,
,
解得,符合题意;
②当时,点从原点开始以每秒3个单位长度的速度沿数轴向右运动,
此时点表示的数为,点表示的数为,
,
,
当时,,
解得;
当时,,
解得,不符合题意,舍去;
综上所述,当时的运动时间的值为2或秒.
21世纪教育网(www.21cnjy.com)
七年级上册数学期末考试押题卷华东师大版2025—2026学年
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.如果将作为标准身高,低于标准身高记作,那么身高应记作( )
A. B. C. D.
2.在同一平面内,若,,则的度数是( )
A.15° B.105° C.25°或105° D.15°或105°
3.的相反数是( )
A.2025 B. C. D.
4.已知单项式与的和仍是单项式,则( )
A.6 B.5 C.4 D.3
5.如图,已知直线,平分,若,则的度数为( )
A. B. C. D.
6.如果代数式的值是,则代数式的值是( )
A. B.4 C. D.2
7.如果,那么是( )
A.正数 B.负数 C.非正数 D.非负数
8.如图是某种细胞分裂示意图,这种细胞经过 1 次分裂便由 1 个分裂成 2 个.根据此规律,一个细胞经过 5 次分裂后可分裂成( )个细胞
A.10 B.16 C.32 D.64
9.如图,线段,动点P从A出发,以的速度沿运动,M为的中点,N为的中点.以下说法正确的是( )
①运动后,;
②的值随着运动时间的改变而改变;
③的值不变;
④当时,运动时间为.
A.①② B.②③ C.①②③ D.②③④
10.如图,直线,相交于点,,,平分,给出下列结论:①当时,;②为的平分线;③与相等的角有3个;④.其中正确的结论为()
A.①②④ B.②③④ C.①③④ D.①②③④
二、填空题(6小题,每题3分,共18分)
11.把数精确到百分位后的近似数是 .
12.的系数是 .
13.如图所示,AD∥BC,BD平分∠ABC,若∠A=110°,则∠D= .
14.若∠A=50°,则∠A的补角为 .
15.在数轴上,点A表示的数是5,若点B与点A之间距离是8,则点B表示的数是 .
16.如果整式A与整式的和为实数,我们称A,为的“友好整式”,例如:与为1的“友好整式”;与为7的“友好整式”.若关于的整式与为的“友好整式”,则的值为 .
第II卷
七年级上册数学期末考试押题卷华东师大版2025—2026学年
名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:.
18.先化简,再求值:,其中,.
19.如图: .
(1)若,求的度数:
(2)若,求的度数.
20.如图,已知点为线段上一点,,,、分别是、的中点.求:
(1)求的长度;
(2)求的长度;
(3)求的长度;
21.如图,在四边形中.点为延长线上一点,点为延长线上一点,连接,交于点,交于点,若,求证:.
证明:
∵( ),
(已知).
∴ = (等量代换).
∴( ).
∴( ).
∵(已知),
∴(等量代换).
∴ (同旁内角互补,两直线平行).
∴( ).
22.为鼓励节约用水,某地推行阶梯式水价,标准如下表所示:
月用水量 不超过17吨 超过17吨且不超过30吨的部分 超过30吨的部分
收费标准(元/吨) a b c
(1)甲居民上月用水20吨,应缴水费 元;(直接写出结果)
(2)乙居民上月用水35吨,应缴水费 元;(直接写出结果)
(3)丙居民上月用水x(x>30)吨,当a=2,b=2.5,c=3时,应缴水费多少元?(用含x的代数式表示)
23.由几个相同的、棱长为2的小立方块搭成的几何体如图所示,将它摆放在桌面上.
(1)画出这个几何体的三视图;
(2)求出这个几何体的表面积.
24.已知射线平分,点C为上任意一点,过点C作直线交射线于点D.
(1)如图1,若,则_________°;
(2)点E是射线上一动点(不与点C,D重合),平分交于点F,过点F作交于点G.
①如图2,若,当时,求的度数;
②当点E在运动过程中,设,,直接写出和之间的数量关系.
25.如图1,、两点在数轴上对应的数分别为和6.
(1)直接写出、两点之间的距离___;
(2)若在数轴上存在一点,使得,求点表示的数;
(3)如图2,现有动点、,若点从点出发,以每秒4个单位长度的速度沿数轴向右运动,同时点从点出发,以每秒2个单位长度的速度沿数轴向左运动,当点到达原点后立即以每秒3个单位长度的速度沿数轴向右运动,求:当时的运动时间的值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A C A B C C D C
二、填空题
11.
【分析】根据四舍五入法将题目中的数据精确到百分位即可.
【详解】解:把数精确到百分位后的近似数是,
故答案为:.
12.
【分析】本题主要考查了单项式的系数的定义,单项式中数字因数叫做这个单项式的系数,据此可得答案.
【详解】解:的系数是,
故答案为:.
13.35°/35度
【分析】根据平行线的性质先求得∠ABC的度数,再根据角平分线的性质及平行线的性质求得∠D的度数.
【详解】∵AD∥BC,∠A=110°,
∴∠ABC=180-∠A=70°;
又∵BD平分∠ABC,
∴∠DBC=35°;
∵AD∥BC,
∴∠D=∠DBC=35°.
故答案为35°.
14.130°
【分析】根据互为补角的两个角的和等于180°列式计算即可得解.
【详解】∠A的补角=180°﹣∠A=180°﹣50°=130°.
故答案为:130°.
15.-3或13
【分析】根据数轴上到一点距离相等的点有两个,分别位于该点的左右,可得答案.
【详解】在数轴上,点A表示数5,点B到点A的距离为8,则点B表示的数是 3或13.
故答案为 3或13.
16.7
【分析】本题主要考查整式的加减运算,掌握整式的加减运算法则成为解题的关键.
根据“友好整式”的定义可知的值与x无关,从而可求出k和n的值即可.
【详解】解:由题意可知:
,
令,得,
∴.
故答案为:7.
三、解答题
17.
【分析】本题考查了有理数的混合运算,绝对值的化简,熟悉掌握运算法则是解题的关键.
先运算乘方运算和化简绝对值,再运算乘除,最后运算加减即可.
【详解】解:
.
18.,
【分析】本题主要考查整式的化简,先去括号,然后合并同类项,最后把,的值代入即可.
【详解】解:
,
当,时,原式.
19.(1)
(2)
【分析】本题考查互余的定义,几何图形中角度的计算,熟练掌握各个角之间的互余和数量关系是解决问题的关键.
(1)根据,结合图形即可求出结论;
(2)根据,结合题意得出各个角度,再根据即可得出结论.
【详解】(1)解:,
由可得,
,
;
(2)解:由(1)知,
,,
,解得,
∴,,
.
20.(1)
(2)
(3)
【分析】本题考查了关于线段的中点的计算,线段的和与差的计算,读懂题意熟练运用线段的和差倍分是解本题的关键.
(1)直接根据是的中点可得答案;
(2)先求出的长,然后根据E是的中点求出,
(3)根据即可求出.
【详解】(1)解:∵,点D是的中点,
∴;
(2)∵,,
∴,
∵E是的中点,
∴,
(3)∵,
∴.
21.对顶角相等;;同位角相等,两直线平行;两直线平行,同旁内角互补;;两直线平行,内错角相等
【分析】运用平行线的判定与性质进行求解即可得出答案.
【详解】证明:∵(对顶角相等),
(已知),
∴(等量代换),
∴(同位角相等,两直线平行),
∴(两直线平行,同旁内角互补),
∵(已知),
∴(等量代换),
∴(同旁内角互补,两直线平行),
∴(两直线平行,内错角相等),
故答案为:对顶角相等;;同位角相等,两直线平行;两直线平行,同旁内角互补;;两直线平行,内错角相等.
22.(1)17a+3b(2)17a+13b+5c(3)3x-23.5
【分析】(1)上月用水20吨,则按照分为两部分,17吨部分和超过17吨的3吨部分,分别计算费用再求和.
(2)上月用水35吨,则按照三部分,17吨部分与30-17=13吨部分与35-30=5吨部分,分别计算费用在求和.
(3)根据(2)得出的代数式,把a,b,c的值代入即可得到.
【详解】(1)20<30,则分两部分,17吨部分价格为17a,超过17吨且不超过30吨的部分价格为(20-17)×b=3b.即应缴税费为17a+3b(元)
(2)35>30,则分为三部分,17吨部分价格为17a,超过17吨且不超过30吨的部分价格为(30-17)×b=13b,超过30吨的部分价格为(35-30)×c=5c.即应缴水费为17a+13b+5c(元)
(3)由(2)知,水量大于30吨时,水费为17a+13b+(x-30)c,把a=2,b=2.5,c=3代入得到,17a+13b+5c=17×2+13×2.5+(x-30)×3=3x-23.5(元)
23.(1)见解析
(2)88
【分析】本题考查了三视图的画法以及表面积的求法.主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,物体的表面积是指露在外部的所有表面积之和.
(1)分别画出从正面,上面,左面看到的图形即可;
(2)根据三视图求解六个面的面积和即可.
【详解】(1)解:画图如下:
;
(2)解:;
24.(1)60
(2)①;②或
【分析】本题考查平行线的性质,三角形内角和定理,也考查了角平分线的定义.
(1)根据角平分线的定义和平行线的性质即可求解;
(2)①由三角形内角和定理可得,由平行线的性质和角平分线的定义可得,,根据即可求解;②分为点在线段上和点在下方两种情况讨论,结合平行线的性质和角平分线的定义即可求解.
【详解】(1)解:∵,,
∴,
∵平分,
∴,
∴;
(2)解:①∵,,
∴,
∵,
∴,
∵平分,
∴,
∴,
∵平分,
∴,
∵,
∴;
②如图,点在线段上,
∵,
∴,
∵平分,平分,
∴,,
∵,
∴
,
∴,
如图,点在下方,
∵,
∴,
∵平分,平分,
∴,,
∵,
∴
,
即.
25.(1)22
(2)或
(3)当时的运动时间的值为2或秒
【分析】(1)根据两点间的距离公式即可求出、两点之间的距离;
(2)设点表示的数为.分两种情况:①点在线段上;②点在线段的延长线上.根据列出关于的方程,求解即可;
(3)根据点的运动方向分两种情况:①当时,点从点出发,以每秒2个单位长度的速度沿数轴向左运动;②当时,点从原点开始以每秒3个单位长度的速度沿数轴向右运动,根据列出关于的方程,解方程即可.
【详解】(1)解:、两点之间的距离是:;
(2)解:设点表示的数为.分两种情况:
①当点在线段上时,
,
,
解得;
②当点在线段的延长线上时,
,
,
解得.
综上所述,点表示的数为或;
(3)解:分两种情况:
①当时,点从点出发,以每秒2个单位长度的速度沿数轴向左运动,
此时点表示的数为,点表示的数为,
,
,
解得,符合题意;
②当时,点从原点开始以每秒3个单位长度的速度沿数轴向右运动,
此时点表示的数为,点表示的数为,
,
,
当时,,
解得;
当时,,
解得,不符合题意,舍去;
综上所述,当时的运动时间的值为2或秒.
21世纪教育网(www.21cnjy.com)
同课章节目录
