七年级上册数学期中考试调研检测卷(含解析)华东师大版2025—2026学年
文档属性
| 名称 | 七年级上册数学期中考试调研检测卷(含解析)华东师大版2025—2026学年 |  | |
| 格式 | docx | ||
| 文件大小 | 610.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 09:08:27 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
七年级上册数学期中考试调研检测卷华东师大版2025—2026学年考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.中国是最早采用正负数表示相反意义的量的国家,如果将“收入60元”记作“元”,那么“支出40元”记作( )
A.元 B.元 C.元 D.20元
2.在,,0,,,中,负数有( )个
A.1 B.2 C.3 D.4
3.某种苹果的售价是元/kg(),现用100元买5kg这种苹果,应找回( )
A.元 B.元 C.元 D.元
4.某市冬季的一天,中午12时的气温是,经过6小时气温下降了,那么当天18时的气温是( )
A. B. C. D.
5.已知,,且,则( )
A. B. C.或- D.
6.单项式的系数和次数是( )
A.系数是,次数是 B.系数是,次数是
C.系数是,次数是 D.系数是,次数是
7.若单项式与是同类项,则m,n的值分别是( )
A.1, B.1,2 C.1, D.1,1
8.若整式的值为8,那么整式的值是( )
A. B. C.14 D.
9.在数轴上有四个互不相等的有理数,,,,若,且在,之间,则化简的结果是( )
A. B. C. D.
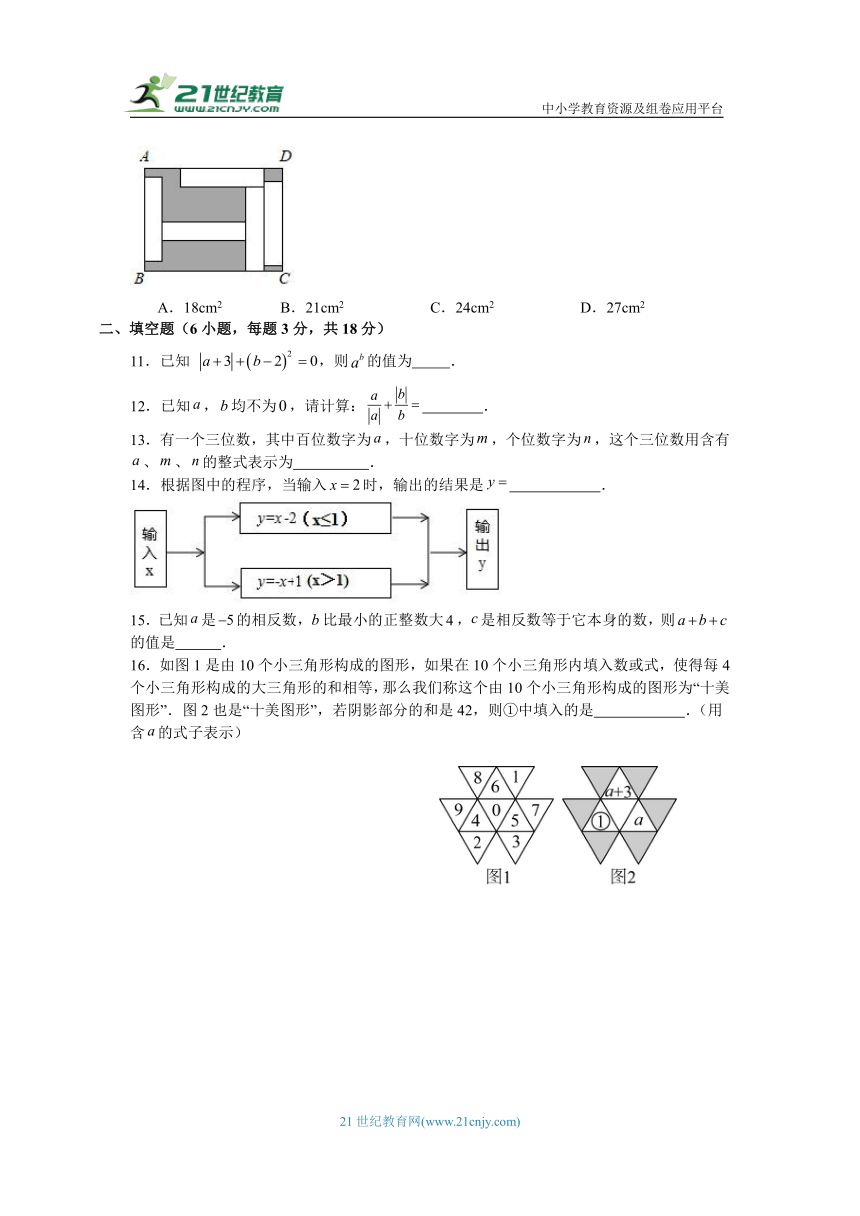
10.在长方形ABCD中,放入5个形状大小相同的小长方形(空白部分),其中AB=7cm,求阴影部分图形的总面积( )
A.18cm2 B.21cm2 C.24cm2 D.27cm2
二、填空题(6小题,每题3分,共18分)
11.已知 ,则的值为 .
12.已知,均不为,请计算: .
13.有一个三位数,其中百位数字为,十位数字为,个位数字为,这个三位数用含有、、的整式表示为 .
14.根据图中的程序,当输入时,输出的结果是 .
15.已知是的相反数,比最小的正整数大,是相反数等于它本身的数,则的值是 .
16.如图1是由10个小三角形构成的图形,如果在10个小三角形内填入数或式,使得每4个小三角形构成的大三角形的和相等,那么我们称这个由10个小三角形构成的图形为“十美图形”.图2也是“十美图形”,若阴影部分的和是42,则①中填入的是 .(用含的式子表示)
第II卷
七年级上册数学期中考试调研检测卷华东师大版2025—2026学年
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23
17.先去括号、再合并同类项
① ②
18.计算:
(1);
(2).
19.先化简,再求值:,其中.
20.某供电局路线检修班乘汽车沿南北方向检修路线,检修班的记录员把当天行车情况记录如下:
到达地点 起点
前进方向 北 南 北 北 南 北 南 北 南 北
所走路程(km) 0 10 4 6 2 5 12 3 9 10 7
(1)求地与起点之间的路程有多少千米;
(2)若汽车每千米耗油0.12升,这天检修班从起点开始,最后到达地,一共耗油多少升?(精确到0.1升)
21.如图,学校要利用专款建一长方形的自行车停车场,该停车场其中一面靠墙,其他三面由护栏围成,其中段护栏长为米,段护栏比段护栏短米.
(1)用、表示长方形停车场段护栏的长度;
(2)求护栏的总长度;
(3)若,,每米护栏造价元,求购买护栏所需的总费用.
22.请阅读材料:
代数式的值为8,求代数式的值为 .
【阅读理解】小明在做作业时采用的方法如下:
由题意得,则有,
.
所以代数式的值为2.
【方法运用】
(1)若,则代数式的值为 .
(2)若代数式的值为5,求代数式的值.
(3)当时,代数式的值为7,当时,求代数式的值.
23.已知代数式:.
(1)化简;
(2)当时,求的值;
(3)若的值与x的取值无关,求y的值.
24.结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示2和5两点之间的距离是_______;表示和2两点之间的距离是_______;一般地,数轴上表示数m和数n的两点之间的距离等于;
(2)如果,请计算x的值;
(3)若,,且数a、b在数轴上表示的数分别是点A、点B,求A、B两点之间的最大距离和最小距离.
(4)若数轴上表示数a的点位于与5之间,则的值是多少?
25.如图,在数轴上A点表示数a,B点表示数b,C点表示数c,b是最小的正整数,且a、c满足.
(1) ______,______,______;
(2)若将数轴折叠,使得A点与C点重合,则点B与数______对应的点重合;
(3)若点A、B、C是数轴上的动点,点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,点A与点B之间的距离表示为,点B与点C之间的距离表示为,那么的值是否随着运动时间t(秒)的变化而改变?若变化,请说明理由:若不变,求出其值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B D C B A C D D
二、填空题
11.
【分析】根据绝对值的非负数,平方的非负性求得的值,进而根据有理数的乘方进行计算即可求解.
【详解】解:∵,
∴,
解得,
∴,
故答案为:.
12.0或2或
【分析】分别讨论,;,;,;,即可求解.
【详解】解:当,时,;
当,时,;
当,时,;
当,时,;
综上所述,或或,
故答案为:0或2或.
13.
【分析】根据是三位数百位上的数字十位上的数字个位上的数字进行解答即可.
【详解】解:根据题意,这个三位数可以表示为,
故答案为:.
14.-1
【分析】由图中的程序知:当x=2时,对应的代数式应该是-x+1,因此可将x的值直接代入所求的代数式中,即可得出结果.
【详解】解:∵x=2,∴x>1;
∴应代入的代数式为-x+1;
得:-x+1=-2+1=-1.
故填-1.
15.
【分析】本题考查相反数的定义,掌握最小的正整数是,相反数等于它本身的数是,熟练掌握以上知识点是解题的关键;
根据,最小的正整数是,相反数等于它本身的数是,进行求解即可.
【详解】解:是的相反数,
,
是相反数等于它本身的数,
故,
,
故答案为:
16.
【分析】本题考查了列代数式表达式以及整式的加减运算,先分别表示,, ,再代入
,化简计算,即可作答.
【详解】解:如图,分别用①,②,…,⑦表示相应位置应填入的式子,
则由题意知: ,
, .
,
解得.
①中填入的是.
故答案为:
三、解答题
17.①-a-5b+5c;②7a2b-10ab2.
【分析】根据括号前是正号,去掉括号及正号,括号里的各项都不变,括号前是负号,去掉括号及负号,括号里的各项都变号,可得答案.
【详解】解:①原式=2a-2b+2c-3a-3b+3c
=(2a-3a)+(-2b-3b)+(2c+3c)
=-a-5b+5c;
②原式=3a2b-2(ab2-2a2b+4ab2)
=3a2b-10ab2+4a2b
=7a2b-10ab2.
18.(1)28
(2)
【分析】本题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序.
(1)根据有理数的乘除法可以解答本题;
(3)先算乘方,再算乘法,最后算加减;如果有括号,要先做括号内的运算.
【详解】(1)解:
;
(2)解:
.
19.,5
【分析】本题主要考查了整式加减的化简求值,
先去括号,再合并同类项,然后代入求值即可.
【详解】解:原式
.
当时,原式.
20.(1)地与起点之间的路程有24千米
(2)一共耗油约8.2升
【分析】本题考查了正数和负数的应用.
(1)规定向北为正,向南为负,把所有的数据相加,然后根据有理数的加法运算法则进行计算即可得解;
(2)求出行驶的路程的和,然后乘以每千米耗油0.12升,进行计算即可得解.
【详解】(1)解:规定向北为正,向南为负,由题意得
(千米),
答:地与起点之间的路程有24千米;
(2)解:
(升).
答:一共耗油约8.2升.
21.(1)米;
(2)米;
(3)元.
【分析】本题考查了整式的加减、列代数式和代数式求值,解题的关键是数形结合.
(1)根据“段护栏比段护栏短米”即可求解;
(2)护栏的长度宽与围墙平行的一边长;
(3)把,的值代入()中的代数式进行求值即可.
【详解】(1)解:宽为:(米),
停车场段护栏的长度为米;
(2)解:护栏的总长度:
(米),
护栏的总长度为米;
(3)解:将,,代入中得:
(米),
所需费用:(元),
购买护栏所需的总费用为元.
22.(1)4
(2)0
(3)
【分析】本题主要考查了代数式求值,理解题中给出的方法,整体代入求值是解题的关键.
(1)然后把变形为,最后整体代入求值即可;
(2)由题意得,然后把变形为,再整体代入求值即可;
(3)把代入代数式,根据其值为7得出,再把代入代数式中,得到,最后整体代入求值即可.
【详解】(1)解:∵,
∴,
故答案为:4;
(2)解:∵,
∴,
∴;
(3)解:当时,代数式的值为7,
∴,即,
当时,代数式.
23.(1)
(2)
(3)的值是
【分析】本题考查了整式的加减、化简求值;
(1)利用去括号法则、整式的加减运算法则计算出答案;
(2)根据题意求出、的值,然后整体代入计算即可;
(3)根据的值与的取值无关,得出的系数和为零,即可得出答案.
【详解】(1)解:,
;
(2)解:∵
∴,,
∴,,
∴原式;
(3)解:,
当的值与的取值无关时,
∴,
解得,
即的值是.
24.(1)3,4;
(2)或;
(3)12或2;
(4)8.
【分析】本题考查了数轴与绝对值的综合题,化简绝对值:
(1)运用右边的数减去左边的数,即可作答;
(2)根据绝对值的性质化简,分类讨论:x在的右边时,或x在的左边;即可作答;
(3)根据绝对值的性质化简,分类讨论,即可作答;
(4)依题意,先得,结合数轴,即可作答
【详解】(1)解:依题意,;
数轴上表示2和5两点之间的距离是3;表示和2两点之间的距离是4;
(2)解:由得,,
所以表示x与距离为2,
当x在的右边时,;
当x在的左边时,;
因为与距离为2的是1或,
所以或;
(3)解:由,得,,,
所以表示a与3的距离为4,b与的距离为3,
同理当a在3的右边时,;
当a在3的左边时,;
当b在的右边时,;
当b在的左边时,;
所以或,或,
当,时,则A、B两点间的最大距离是12,
当,时,则A、B两点间的最小距离是2;
(4)解:
所以表示a与的距离加上a与5的距离的和,
因为表示数a的点位于与5之间,
所以.
25.(1),,;
(2)4;
(3)不变,值为12.
【分析】(1)根据绝对值的非负性进行解答即可得;
(2)根据折叠的性质进行解答即可得;
(3)根据题意可得,t秒钟后,A点表示,B点表示,C点表示,
,,即可得.
【详解】(1)解:∵
∴,,即,,
由b是最小的正整数可得,
故答案为:,,;
(2)解:,
,
故答案为:4
(3)解:不变,值为12,
t秒钟后,A点表示,B点表示,C点表示,
则,,
,
21世纪教育网(www.21cnjy.com)
七年级上册数学期中考试调研检测卷华东师大版2025—2026学年考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.中国是最早采用正负数表示相反意义的量的国家,如果将“收入60元”记作“元”,那么“支出40元”记作( )
A.元 B.元 C.元 D.20元
2.在,,0,,,中,负数有( )个
A.1 B.2 C.3 D.4
3.某种苹果的售价是元/kg(),现用100元买5kg这种苹果,应找回( )
A.元 B.元 C.元 D.元
4.某市冬季的一天,中午12时的气温是,经过6小时气温下降了,那么当天18时的气温是( )
A. B. C. D.
5.已知,,且,则( )
A. B. C.或- D.
6.单项式的系数和次数是( )
A.系数是,次数是 B.系数是,次数是
C.系数是,次数是 D.系数是,次数是
7.若单项式与是同类项,则m,n的值分别是( )
A.1, B.1,2 C.1, D.1,1
8.若整式的值为8,那么整式的值是( )
A. B. C.14 D.
9.在数轴上有四个互不相等的有理数,,,,若,且在,之间,则化简的结果是( )
A. B. C. D.
10.在长方形ABCD中,放入5个形状大小相同的小长方形(空白部分),其中AB=7cm,求阴影部分图形的总面积( )
A.18cm2 B.21cm2 C.24cm2 D.27cm2
二、填空题(6小题,每题3分,共18分)
11.已知 ,则的值为 .
12.已知,均不为,请计算: .
13.有一个三位数,其中百位数字为,十位数字为,个位数字为,这个三位数用含有、、的整式表示为 .
14.根据图中的程序,当输入时,输出的结果是 .
15.已知是的相反数,比最小的正整数大,是相反数等于它本身的数,则的值是 .
16.如图1是由10个小三角形构成的图形,如果在10个小三角形内填入数或式,使得每4个小三角形构成的大三角形的和相等,那么我们称这个由10个小三角形构成的图形为“十美图形”.图2也是“十美图形”,若阴影部分的和是42,则①中填入的是 .(用含的式子表示)
第II卷
七年级上册数学期中考试调研检测卷华东师大版2025—2026学年
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23
17.先去括号、再合并同类项
① ②
18.计算:
(1);
(2).
19.先化简,再求值:,其中.
20.某供电局路线检修班乘汽车沿南北方向检修路线,检修班的记录员把当天行车情况记录如下:
到达地点 起点
前进方向 北 南 北 北 南 北 南 北 南 北
所走路程(km) 0 10 4 6 2 5 12 3 9 10 7
(1)求地与起点之间的路程有多少千米;
(2)若汽车每千米耗油0.12升,这天检修班从起点开始,最后到达地,一共耗油多少升?(精确到0.1升)
21.如图,学校要利用专款建一长方形的自行车停车场,该停车场其中一面靠墙,其他三面由护栏围成,其中段护栏长为米,段护栏比段护栏短米.
(1)用、表示长方形停车场段护栏的长度;
(2)求护栏的总长度;
(3)若,,每米护栏造价元,求购买护栏所需的总费用.
22.请阅读材料:
代数式的值为8,求代数式的值为 .
【阅读理解】小明在做作业时采用的方法如下:
由题意得,则有,
.
所以代数式的值为2.
【方法运用】
(1)若,则代数式的值为 .
(2)若代数式的值为5,求代数式的值.
(3)当时,代数式的值为7,当时,求代数式的值.
23.已知代数式:.
(1)化简;
(2)当时,求的值;
(3)若的值与x的取值无关,求y的值.
24.结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示2和5两点之间的距离是_______;表示和2两点之间的距离是_______;一般地,数轴上表示数m和数n的两点之间的距离等于;
(2)如果,请计算x的值;
(3)若,,且数a、b在数轴上表示的数分别是点A、点B,求A、B两点之间的最大距离和最小距离.
(4)若数轴上表示数a的点位于与5之间,则的值是多少?
25.如图,在数轴上A点表示数a,B点表示数b,C点表示数c,b是最小的正整数,且a、c满足.
(1) ______,______,______;
(2)若将数轴折叠,使得A点与C点重合,则点B与数______对应的点重合;
(3)若点A、B、C是数轴上的动点,点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,点A与点B之间的距离表示为,点B与点C之间的距离表示为,那么的值是否随着运动时间t(秒)的变化而改变?若变化,请说明理由:若不变,求出其值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B C B D C B A C D D
二、填空题
11.
【分析】根据绝对值的非负数,平方的非负性求得的值,进而根据有理数的乘方进行计算即可求解.
【详解】解:∵,
∴,
解得,
∴,
故答案为:.
12.0或2或
【分析】分别讨论,;,;,;,即可求解.
【详解】解:当,时,;
当,时,;
当,时,;
当,时,;
综上所述,或或,
故答案为:0或2或.
13.
【分析】根据是三位数百位上的数字十位上的数字个位上的数字进行解答即可.
【详解】解:根据题意,这个三位数可以表示为,
故答案为:.
14.-1
【分析】由图中的程序知:当x=2时,对应的代数式应该是-x+1,因此可将x的值直接代入所求的代数式中,即可得出结果.
【详解】解:∵x=2,∴x>1;
∴应代入的代数式为-x+1;
得:-x+1=-2+1=-1.
故填-1.
15.
【分析】本题考查相反数的定义,掌握最小的正整数是,相反数等于它本身的数是,熟练掌握以上知识点是解题的关键;
根据,最小的正整数是,相反数等于它本身的数是,进行求解即可.
【详解】解:是的相反数,
,
是相反数等于它本身的数,
故,
,
故答案为:
16.
【分析】本题考查了列代数式表达式以及整式的加减运算,先分别表示,, ,再代入
,化简计算,即可作答.
【详解】解:如图,分别用①,②,…,⑦表示相应位置应填入的式子,
则由题意知: ,
, .
,
解得.
①中填入的是.
故答案为:
三、解答题
17.①-a-5b+5c;②7a2b-10ab2.
【分析】根据括号前是正号,去掉括号及正号,括号里的各项都不变,括号前是负号,去掉括号及负号,括号里的各项都变号,可得答案.
【详解】解:①原式=2a-2b+2c-3a-3b+3c
=(2a-3a)+(-2b-3b)+(2c+3c)
=-a-5b+5c;
②原式=3a2b-2(ab2-2a2b+4ab2)
=3a2b-10ab2+4a2b
=7a2b-10ab2.
18.(1)28
(2)
【分析】本题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序.
(1)根据有理数的乘除法可以解答本题;
(3)先算乘方,再算乘法,最后算加减;如果有括号,要先做括号内的运算.
【详解】(1)解:
;
(2)解:
.
19.,5
【分析】本题主要考查了整式加减的化简求值,
先去括号,再合并同类项,然后代入求值即可.
【详解】解:原式
.
当时,原式.
20.(1)地与起点之间的路程有24千米
(2)一共耗油约8.2升
【分析】本题考查了正数和负数的应用.
(1)规定向北为正,向南为负,把所有的数据相加,然后根据有理数的加法运算法则进行计算即可得解;
(2)求出行驶的路程的和,然后乘以每千米耗油0.12升,进行计算即可得解.
【详解】(1)解:规定向北为正,向南为负,由题意得
(千米),
答:地与起点之间的路程有24千米;
(2)解:
(升).
答:一共耗油约8.2升.
21.(1)米;
(2)米;
(3)元.
【分析】本题考查了整式的加减、列代数式和代数式求值,解题的关键是数形结合.
(1)根据“段护栏比段护栏短米”即可求解;
(2)护栏的长度宽与围墙平行的一边长;
(3)把,的值代入()中的代数式进行求值即可.
【详解】(1)解:宽为:(米),
停车场段护栏的长度为米;
(2)解:护栏的总长度:
(米),
护栏的总长度为米;
(3)解:将,,代入中得:
(米),
所需费用:(元),
购买护栏所需的总费用为元.
22.(1)4
(2)0
(3)
【分析】本题主要考查了代数式求值,理解题中给出的方法,整体代入求值是解题的关键.
(1)然后把变形为,最后整体代入求值即可;
(2)由题意得,然后把变形为,再整体代入求值即可;
(3)把代入代数式,根据其值为7得出,再把代入代数式中,得到,最后整体代入求值即可.
【详解】(1)解:∵,
∴,
故答案为:4;
(2)解:∵,
∴,
∴;
(3)解:当时,代数式的值为7,
∴,即,
当时,代数式.
23.(1)
(2)
(3)的值是
【分析】本题考查了整式的加减、化简求值;
(1)利用去括号法则、整式的加减运算法则计算出答案;
(2)根据题意求出、的值,然后整体代入计算即可;
(3)根据的值与的取值无关,得出的系数和为零,即可得出答案.
【详解】(1)解:,
;
(2)解:∵
∴,,
∴,,
∴原式;
(3)解:,
当的值与的取值无关时,
∴,
解得,
即的值是.
24.(1)3,4;
(2)或;
(3)12或2;
(4)8.
【分析】本题考查了数轴与绝对值的综合题,化简绝对值:
(1)运用右边的数减去左边的数,即可作答;
(2)根据绝对值的性质化简,分类讨论:x在的右边时,或x在的左边;即可作答;
(3)根据绝对值的性质化简,分类讨论,即可作答;
(4)依题意,先得,结合数轴,即可作答
【详解】(1)解:依题意,;
数轴上表示2和5两点之间的距离是3;表示和2两点之间的距离是4;
(2)解:由得,,
所以表示x与距离为2,
当x在的右边时,;
当x在的左边时,;
因为与距离为2的是1或,
所以或;
(3)解:由,得,,,
所以表示a与3的距离为4,b与的距离为3,
同理当a在3的右边时,;
当a在3的左边时,;
当b在的右边时,;
当b在的左边时,;
所以或,或,
当,时,则A、B两点间的最大距离是12,
当,时,则A、B两点间的最小距离是2;
(4)解:
所以表示a与的距离加上a与5的距离的和,
因为表示数a的点位于与5之间,
所以.
25.(1),,;
(2)4;
(3)不变,值为12.
【分析】(1)根据绝对值的非负性进行解答即可得;
(2)根据折叠的性质进行解答即可得;
(3)根据题意可得,t秒钟后,A点表示,B点表示,C点表示,
,,即可得.
【详解】(1)解:∵
∴,,即,,
由b是最小的正整数可得,
故答案为:,,;
(2)解:,
,
故答案为:4
(3)解:不变,值为12,
t秒钟后,A点表示,B点表示,C点表示,
则,,
,
21世纪教育网(www.21cnjy.com)
同课章节目录
