2024新人教版七年级上数学 4.1 整式 第2课时 多项式 课件(共33张PPT)
文档属性
| 名称 | 2024新人教版七年级上数学 4.1 整式 第2课时 多项式 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 11.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-23 05:32:51 | ||
图片预览









文档简介
(共33张PPT)
人教版(2024)
七年级上册
4.1 整式
第2课时 多项式
第四章 · 整式的加减
多项式
知识目标
1.能够准确叙述并理解多项式、多项式的项、次数等核心概念;明确整式的定义及其与单项式、多项式的关系。
2.能区分单项式、多项式和整式。
3.正确书写多项式的标准形式。
能力目标
1.让学生经历从具体问题中提取其中的多项式结构,培养数学建模意识。
2.通过对比单项式与多项式的异同,归纳整式的共性特征,提升分类讨论的思维能力
素质目标
1.养成仔细审题的习惯,避免混淆“项”与“系数”“次数”等易错点。
2.在小组活动中分享观点,倾听他人思路,形成批判性思维和团队协作精神。
教学难点
教学重点
多项式的定义、项的判定、次数的确定方法
准确判断多项式的次数
知识讲解
03
对应练习
05
情景创设
01
课堂小结
07
例题讲解
04
链接中考
06
新知探索
02
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
复习旧知
单项式的概念
由数或字母的积组成的代数式叫作单项式.单独的一个数或一个字母也是单项式.
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
复习旧知
单项式的系数
我们把单项式中的数字因数叫做这个单项式的系数.
单项式的次数
一个单项式中,所有字母的指数的和叫作这个单项式的次数.如果一个单项式的次数是n,那么称这个单项式是n次单项式.
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
情境:巧手剪纸——“剪春”
“剪春”通常指的是在春节或立春时节,人们通过剪纸艺术来创作“春”字这一传统习俗。
“春”字在剪纸艺术中,往往被赋予吉祥、喜庆、幸福和希望的寓意。它代表着新生、繁荣与活力,预示着万物复苏、生机勃勃的春天即将到来。
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
情境:巧手剪纸——“剪鱼”
在剪纸艺术中,“鱼”常常与“余”谐音,用来表达“连年有余”“年年有余”等寓意,象征着人们对生活富足、财富绵延的期盼。
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
列举实例
根据要求列代数式:
1
假设剪一个小的‘春’字需要2分钟,那么剪x个小的‘春’字需要多少分钟?
2
假设剪一个‘鱼’图案需要3分钟,那么剪y个‘鱼’需要多少分钟?
3
这幅作品里,既有‘春’字,也有‘鱼’,总共耗时多少分钟?
2x
3y
2x+3y
单项式
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
情境:了解“算盘”
算盘是一种简便的计算工具,能进行加减乘除及开平方、开立方等复杂计算。其独特的“五升十进制”计算方式,简化了计算步骤,计算速度快,曾是商业、金融、工程等领域不可或缺的核心工具。
2013年12月4日,联合国教科文组织正式将中国珠算列入人类非物质文化遗产名录。这一决定不仅是对珠算这一古老计算工具的认可,更是对其深厚文化内涵和历史价值的肯定。
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
列举实例
根据要求列代数式:
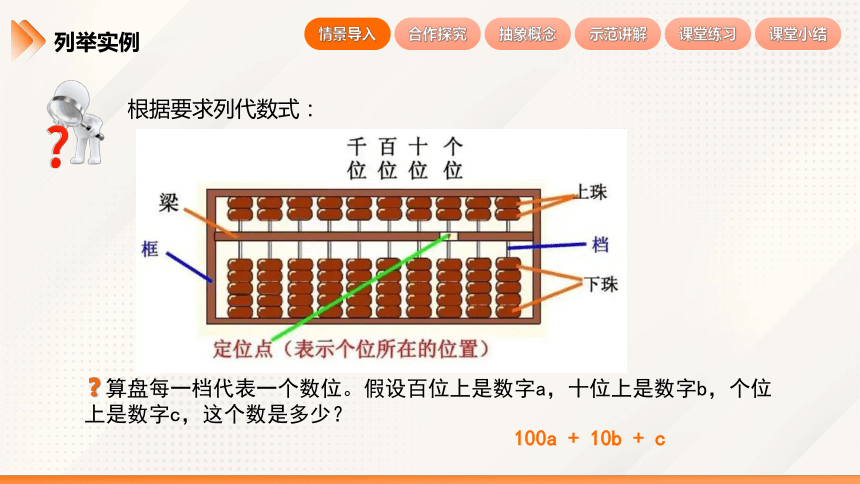
算盘每一档代表一个数位。假设百位上是数字a,十位上是数字b,个位上是数字c,这个数是多少?
100a + 10b + c
分析问题,寻找对应
100a + 10b + c这个式子和我们刚才的2x + 3y有什么共同点?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
它们都是由几个单项式通过加法运算组合起来的式子
它们都是用字母来表示数的式子
多项式
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
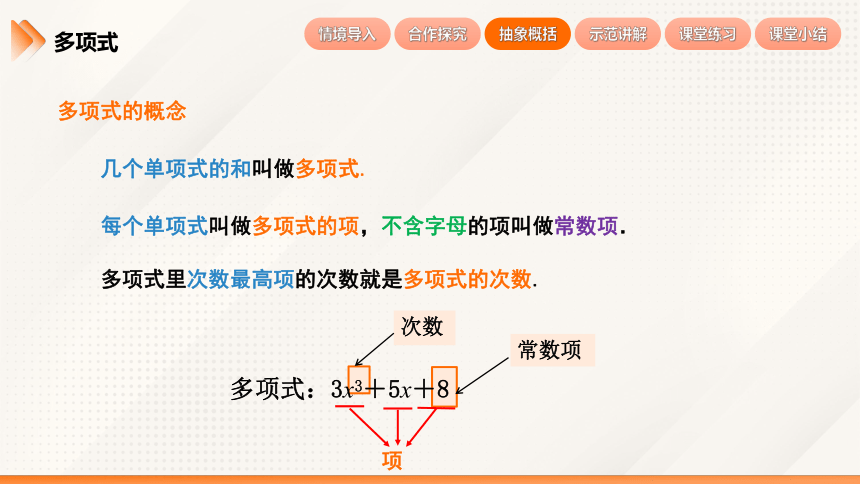
多项式的概念
几个单项式的和叫做多项式.
每个单项式叫做多项式的项,不含字母的项叫做常数项.
多项式:3x3+5x+8
常数项
次数
多项式里次数最高项的次数就是多项式的次数.
项
多项式
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
整式的概念
单项式和多项式统称整式.
单项式
多项式
整式
如果一个式子既不是单项式也不是多项式,那么它一定不是整式.
多项式
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1. 多项式的各项应包括它前面的符号.
3. 要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的.
4. 一个多项式的最高次项可以不唯一.
2. 多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号.
注意
如18a2+4ab
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
请列出下列问题中的代数式,并指出其中:①哪些是单项式?单项式的系数和次数分别是多少 ②哪些是多项式 多项式的次数是多少
(1)如图,一个十字形花坛铺满了草皮,这个花坛草地面积是多少?
例1
解
这个花坛草地面积是ab-4c2。
ab-4c2是多项式,次数是2。
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
(2)当水结冰时,其体积大约会比原来增加,x m 的水结成冰后体积是多少
(3)如图,一个长方体的箱子紧靠墙角,它的长、宽、
高分别是a,b,c。这个箱子露在外面的表面积是多
少?
例1
解:(3)表面积是ac+bc+ab; 是多项式,次数是2。
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例2
用多项式填空,并指出它们的项和次数.
(1)一个长方形相邻两条边的长分别为a,b,则这个长方形的周长为 .
2a+2b
(2)m为一个有理数,m的立方与2的差为 .
解:(1)2a+2b,它的项分别为2a,2b,次数是1.
解:(2)m3-2,它的项分别为m3,-2,次数是3.
m3-2
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例2
用多项式填空,并指出它们的项和次数.
(3)某公司向某地投放共享单车,前两年每年投放a辆,为环保和安全起见,从第三年年初起不再投放,且每个月回收6辆. 第三年年底,该地区共有这家公司的共享单车的辆数为 .
解:(3)2a-12b,它的项分别为2a,-12b,次数是1.
2a-12b
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例2
用多项式填空,并指出它们的项和次数.
(4)现存于陕西历史博物馆的我国南北朝时期的官员独孤信的印章如下图所示,它由18个相同的正方形和8个相同的等边三角形围成. 如果其中正方形和等边三角形的边长都为a,等边三角形的高为b,那么这个印章的表面积为 .
解:(4)18a2+4ab,它的项分别为18a2,4ab,次数是2.
18a2+4ab
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
下列式子中,哪些是整式?哪些是单项式?哪些是多项式?
例3
解
单项式:
多项式:
整式:
a,-5,π
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例4
解
已知-5xm+104xm-4xmy2是关于x、y的六次多项式,求m的值,并写出该多项式.
由题意得最高次数m+2=6,
解得 m=4,
∴此多项式是-5x4+104x4-4x4y2.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
多项式的项:a5,﹣a2b,ab,﹣b3.
1. 指出下列多项式的项和次数.
a5﹣a2b+ab﹣b3
解:
各单项式的次数依次为:5, 3, 2, 3.
多项式的次数: 5
2.如果一个多项式是五次多项式,那么( )
A.这个多项式最多有六项
B.这个多项式只能有一项的次数是五
C.这个多项式一定是五次六项式
D.这个多项式最少有二项,并且最高次项的次数是五
D
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
解:(1) x3-x+1是三次三项式。
(2) x3-2x2y2+3y2是四次三项式。
补充:多项式x3-2x2y2+3y2 的项有____项,分别是___________________,其中四次项的系数是_____,二次项是______,次数最高的项是_________.
三
x3、-2x2y2、3y2
-2
3y2
-2x2y2
3.指出下列多项式是几次几项式:
(1) x3-x+1; (2) x3-2x2y2+3y2。
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
4.下列代数式中哪些是单项式?哪些是多项式?分别填入所属的圈中.
单项式
多项式
4r2,3
2a+1,2x2-5y+1,
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
5. 下列整式中哪些是单项式?哪些是多项式?
是单项式的指出系数和次数,是多项式的指出项和次数:
单项式
系数
次数
x
32t3
1
32
1
3
0
6
3
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
6.鲁班锁是我国古代传统建筑的固定结合器,也是一种广泛流传的益智玩具(如图(1)),其中六根鲁班锁中一个构件的一个面的尺寸如图(2),这个面的面积为_________.
ab-cd
(1)
(2)
链接中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
(2023·河北)现有甲、乙、丙三种矩形卡片各若干张,卡片的边长如图1所示(a>1).某同学分别用6张卡片拼出了两个矩形(不重叠无缝隙),如图2和图3,其面积分别为S1,S2.
请用含a的式子分别表示S1,S2;当a=2时,求S1+S2的值
链接中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
请用含a的式子分别表示S1,S2;当a=2时,求S1+S2的值
解:依题意得,三种矩形卡片的面积分别为:S甲=a ,
S乙=a,
S丙=1,
S1= S甲+3S乙+2S丙=a2+3a+2,S2=5S乙+S丙=5a+1,
S1+S2=(a2+3a+2)+(5a+1) =a2+8a+3,
当a=2时,S1+S2=22+8x2+3=23;
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
我亲历了什么
我知道了什么
我会什么
理解多项式、整式的概念
确定一个多项式的次数
从具体问题中提取其中的多项式结构
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
多项式的概念
几个单项式的和叫做多项式.
每个单项式叫做多项式的项,不含字母的项叫做常数项.
多项式里次数最高项的次数就是多项式的次数.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
整式的概念
单项式和多项式统称整式.
单项式
多项式
整式
如果一个式子既不是单项式也不是多项式,那么它一定不是整式.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
课后作业
A层:P94:习题4.1:第3、4题;
B层:P94:习题4.1:第7、9题.
下 课
人教版(2024)
七年级上册
4.1 整式
第2课时 多项式
第四章 · 整式的加减
多项式
知识目标
1.能够准确叙述并理解多项式、多项式的项、次数等核心概念;明确整式的定义及其与单项式、多项式的关系。
2.能区分单项式、多项式和整式。
3.正确书写多项式的标准形式。
能力目标
1.让学生经历从具体问题中提取其中的多项式结构,培养数学建模意识。
2.通过对比单项式与多项式的异同,归纳整式的共性特征,提升分类讨论的思维能力
素质目标
1.养成仔细审题的习惯,避免混淆“项”与“系数”“次数”等易错点。
2.在小组活动中分享观点,倾听他人思路,形成批判性思维和团队协作精神。
教学难点
教学重点
多项式的定义、项的判定、次数的确定方法
准确判断多项式的次数
知识讲解
03
对应练习
05
情景创设
01
课堂小结
07
例题讲解
04
链接中考
06
新知探索
02
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
复习旧知
单项式的概念
由数或字母的积组成的代数式叫作单项式.单独的一个数或一个字母也是单项式.
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
复习旧知
单项式的系数
我们把单项式中的数字因数叫做这个单项式的系数.
单项式的次数
一个单项式中,所有字母的指数的和叫作这个单项式的次数.如果一个单项式的次数是n,那么称这个单项式是n次单项式.
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
情境:巧手剪纸——“剪春”
“剪春”通常指的是在春节或立春时节,人们通过剪纸艺术来创作“春”字这一传统习俗。
“春”字在剪纸艺术中,往往被赋予吉祥、喜庆、幸福和希望的寓意。它代表着新生、繁荣与活力,预示着万物复苏、生机勃勃的春天即将到来。
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
情境:巧手剪纸——“剪鱼”
在剪纸艺术中,“鱼”常常与“余”谐音,用来表达“连年有余”“年年有余”等寓意,象征着人们对生活富足、财富绵延的期盼。
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
列举实例
根据要求列代数式:
1
假设剪一个小的‘春’字需要2分钟,那么剪x个小的‘春’字需要多少分钟?
2
假设剪一个‘鱼’图案需要3分钟,那么剪y个‘鱼’需要多少分钟?
3
这幅作品里,既有‘春’字,也有‘鱼’,总共耗时多少分钟?
2x
3y
2x+3y
单项式
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
情境:了解“算盘”
算盘是一种简便的计算工具,能进行加减乘除及开平方、开立方等复杂计算。其独特的“五升十进制”计算方式,简化了计算步骤,计算速度快,曾是商业、金融、工程等领域不可或缺的核心工具。
2013年12月4日,联合国教科文组织正式将中国珠算列入人类非物质文化遗产名录。这一决定不仅是对珠算这一古老计算工具的认可,更是对其深厚文化内涵和历史价值的肯定。
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
列举实例
根据要求列代数式:
算盘每一档代表一个数位。假设百位上是数字a,十位上是数字b,个位上是数字c,这个数是多少?
100a + 10b + c
分析问题,寻找对应
100a + 10b + c这个式子和我们刚才的2x + 3y有什么共同点?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
它们都是由几个单项式通过加法运算组合起来的式子
它们都是用字母来表示数的式子
多项式
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
多项式的概念
几个单项式的和叫做多项式.
每个单项式叫做多项式的项,不含字母的项叫做常数项.
多项式:3x3+5x+8
常数项
次数
多项式里次数最高项的次数就是多项式的次数.
项
多项式
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
整式的概念
单项式和多项式统称整式.
单项式
多项式
整式
如果一个式子既不是单项式也不是多项式,那么它一定不是整式.
多项式
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1. 多项式的各项应包括它前面的符号.
3. 要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的.
4. 一个多项式的最高次项可以不唯一.
2. 多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号.
注意
如18a2+4ab
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
请列出下列问题中的代数式,并指出其中:①哪些是单项式?单项式的系数和次数分别是多少 ②哪些是多项式 多项式的次数是多少
(1)如图,一个十字形花坛铺满了草皮,这个花坛草地面积是多少?
例1
解
这个花坛草地面积是ab-4c2。
ab-4c2是多项式,次数是2。
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
(2)当水结冰时,其体积大约会比原来增加,x m 的水结成冰后体积是多少
(3)如图,一个长方体的箱子紧靠墙角,它的长、宽、
高分别是a,b,c。这个箱子露在外面的表面积是多
少?
例1
解:(3)表面积是ac+bc+ab; 是多项式,次数是2。
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例2
用多项式填空,并指出它们的项和次数.
(1)一个长方形相邻两条边的长分别为a,b,则这个长方形的周长为 .
2a+2b
(2)m为一个有理数,m的立方与2的差为 .
解:(1)2a+2b,它的项分别为2a,2b,次数是1.
解:(2)m3-2,它的项分别为m3,-2,次数是3.
m3-2
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例2
用多项式填空,并指出它们的项和次数.
(3)某公司向某地投放共享单车,前两年每年投放a辆,为环保和安全起见,从第三年年初起不再投放,且每个月回收6辆. 第三年年底,该地区共有这家公司的共享单车的辆数为 .
解:(3)2a-12b,它的项分别为2a,-12b,次数是1.
2a-12b
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例2
用多项式填空,并指出它们的项和次数.
(4)现存于陕西历史博物馆的我国南北朝时期的官员独孤信的印章如下图所示,它由18个相同的正方形和8个相同的等边三角形围成. 如果其中正方形和等边三角形的边长都为a,等边三角形的高为b,那么这个印章的表面积为 .
解:(4)18a2+4ab,它的项分别为18a2,4ab,次数是2.
18a2+4ab
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
下列式子中,哪些是整式?哪些是单项式?哪些是多项式?
例3
解
单项式:
多项式:
整式:
a,-5,π
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例4
解
已知-5xm+104xm-4xmy2是关于x、y的六次多项式,求m的值,并写出该多项式.
由题意得最高次数m+2=6,
解得 m=4,
∴此多项式是-5x4+104x4-4x4y2.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
多项式的项:a5,﹣a2b,ab,﹣b3.
1. 指出下列多项式的项和次数.
a5﹣a2b+ab﹣b3
解:
各单项式的次数依次为:5, 3, 2, 3.
多项式的次数: 5
2.如果一个多项式是五次多项式,那么( )
A.这个多项式最多有六项
B.这个多项式只能有一项的次数是五
C.这个多项式一定是五次六项式
D.这个多项式最少有二项,并且最高次项的次数是五
D
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
解:(1) x3-x+1是三次三项式。
(2) x3-2x2y2+3y2是四次三项式。
补充:多项式x3-2x2y2+3y2 的项有____项,分别是___________________,其中四次项的系数是_____,二次项是______,次数最高的项是_________.
三
x3、-2x2y2、3y2
-2
3y2
-2x2y2
3.指出下列多项式是几次几项式:
(1) x3-x+1; (2) x3-2x2y2+3y2。
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
4.下列代数式中哪些是单项式?哪些是多项式?分别填入所属的圈中.
单项式
多项式
4r2,3
2a+1,2x2-5y+1,
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
5. 下列整式中哪些是单项式?哪些是多项式?
是单项式的指出系数和次数,是多项式的指出项和次数:
单项式
系数
次数
x
32t3
1
32
1
3
0
6
3
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
6.鲁班锁是我国古代传统建筑的固定结合器,也是一种广泛流传的益智玩具(如图(1)),其中六根鲁班锁中一个构件的一个面的尺寸如图(2),这个面的面积为_________.
ab-cd
(1)
(2)
链接中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
(2023·河北)现有甲、乙、丙三种矩形卡片各若干张,卡片的边长如图1所示(a>1).某同学分别用6张卡片拼出了两个矩形(不重叠无缝隙),如图2和图3,其面积分别为S1,S2.
请用含a的式子分别表示S1,S2;当a=2时,求S1+S2的值
链接中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
请用含a的式子分别表示S1,S2;当a=2时,求S1+S2的值
解:依题意得,三种矩形卡片的面积分别为:S甲=a ,
S乙=a,
S丙=1,
S1= S甲+3S乙+2S丙=a2+3a+2,S2=5S乙+S丙=5a+1,
S1+S2=(a2+3a+2)+(5a+1) =a2+8a+3,
当a=2时,S1+S2=22+8x2+3=23;
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
我亲历了什么
我知道了什么
我会什么
理解多项式、整式的概念
确定一个多项式的次数
从具体问题中提取其中的多项式结构
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
多项式的概念
几个单项式的和叫做多项式.
每个单项式叫做多项式的项,不含字母的项叫做常数项.
多项式里次数最高项的次数就是多项式的次数.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
整式的概念
单项式和多项式统称整式.
单项式
多项式
整式
如果一个式子既不是单项式也不是多项式,那么它一定不是整式.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
课后作业
A层:P94:习题4.1:第3、4题;
B层:P94:习题4.1:第7、9题.
下 课
同课章节目录
