4.5 相似三角形判定定理的证明 同步练习 2025-2026学年北师大版数学九年级上册(含答案)
文档属性
| 名称 | 4.5 相似三角形判定定理的证明 同步练习 2025-2026学年北师大版数学九年级上册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 224.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 09:43:41 | ||
图片预览


文档简介
4.5 相似三角形判定定理的证明
基础夯实
知识点 相似三角形判定定理的证明
1.「2025山东枣庄市中期中」在△ABC 纸片中,∠ACB=90°,BC=5,AC=7,将该纸片沿虚线剪开,剪下的阴影三角形与原三角形不相似的是 ( )
2.如图,在四边形 ABCD 中, ∠B =∠ACD,AB=6,BC=4,AC=5,CD= ,则AD的长为 .
3.「2024上海中考节选」如图所示,在矩形ABCD中,E为边CD上一点,且AE⊥BD.
求证:
4.我们可以借助两个直角三角形全等的条件,探索两个直角三角形相似的条件.
(1)“对于两个直角三角形,满足一边、一锐角分别相等或两直角边分别相等,这两个直角三角形全 等.”类似 地,可以 得 到“满足 或 的两个直角三角形相似.”
(2)“满足斜边和一条直角边分别相等的两个直角三角形全等.”类似地,可以得到“满足 的两个直角三角形相似.”
(3)如图,在 Rt△ABC 和 Rt△A'B'C'中,∠C = 求证: Rt △ABC ∽Rt△A'B'C'.
5.如图,ARt△ABC中, ∠ABC = 90°, BD ⊥AC,垂足为D,AE平分∠BAC,分别交 BD,BC 于点 F,E.若AB: BC=3:4,则BF:FD为( )
A.5:3 B.5:4 C.4:3 D.2:1
6.如图,在菱形 ABCD 中,∠ABC=60°,对角线 AC 与 BD 相交于点 O,点 F 为BC 的中点,连接AF与BD 相交于点 E,连接CE 并延长交AB于点 G.
(1)证明:△BEF∽△BCO.
(2)证明:△BEG≌△AEG.
7.【问题背景】△ABC 中,AB=AC,∠BAC=90°,P 为BC 上的动点,现将一个含45°角的透明三角尺的45°角的顶点落在点 P 处,使三角尺绕点 P 旋转.
【用数学的眼光观察】(1)如图1,当三角尺的两边分别交 AB、AC 于点 E、F 时,以下结论正确的是
①△BPE≌△CFP;②△BPE∽△CFP;
③∠BEP=∠CPF;
【用数学的思维思考】(2)将三角尺绕点 P 旋转到如图2所示的位置时,三角尺的两边分别交 BA 的延长线、边AC于点 E、F,△BPE 与△CFP 相似吗 请说明理由.
【用数学的语言表达】(3)在(2)的条件下,动点 P运动到什么位置时,△BPE∽△PFE 说明理由.
微专题“三点定形”证明三角形相似
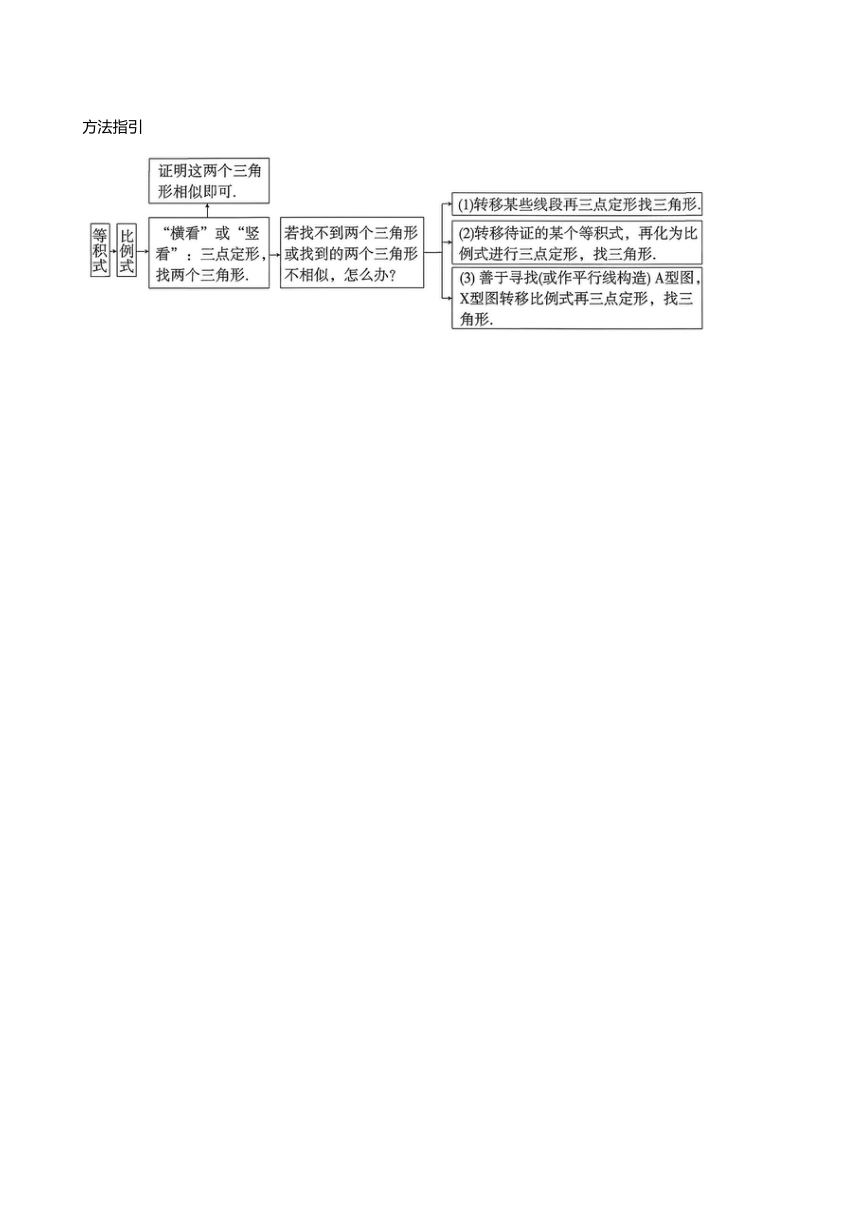
方法指引
1.如图,梯形ABCD中,AD∥BC,AC 与BD 相交于O 点,过点 B 作 BE∥CD交CA 的延长线于点 E.求证:
E
2.如图,在菱形ABCD中,点 G在边 CD上,连接AG 并延长,交 BC 的延长线于点 F,连接BD交AF 于点E,连接CE.
(1)求证:
(2)若 求 CF 的长.
*5相似三角形判定定理的证明
基础夯实
1. D 如图 1,∵ CD ⊥AB 于点 D,.. ∠ADC = 90°,∵ ∠ACB = 90°,∴ ∠ADC = ∠ACB,∵ ∠A = ∠A,∵.△ACD∽△ABC,故A不符合题意;如图2,∵ EF⊥AC,∴∠AFE=90°,∵∠ACB=90°,∴∠AFE=∠ACB,.. EF∥BC,∴ △AEF∽△ABC,故 B 不符合题意;如图3,∵BC=5,AC=7,HC=2.5,GC=3.5,∴HCE=25= ∴△GHC∽△ABC,故 C 不符合题意;如图4,∵BC= KC4C,∴△KLC与△ABC不相似,故D符合题意.故选D.
2答案
解析 ∵AB=6,BC=4,AC=5,CD= ,∴AB=BCAC= 又∵∠B=∠ACD,
∴△ABC∽△DCA,∴∠CD=4B=4/s,
故答案为254.
3.证明 · · 四边形 ABCD 是矩形,∴ ∠BAD = 90°,∠ADE=90°,AB=DC,∴∠ABD+∠ADB=90°,
∵AE⊥BD,∴∠DAE+∠ADB=90°,
∴∠ABD=∠DAE,
∵∠BAD=∠ADE=90°,∴△ADE∽△BAD,
4.解析 (1)一个锐角相等;两直角边成比例.
(2)斜边和一条直角边成比例.
(3)证明:设 则AB=kA'B',AC=kA'C'. 在 Rt △ABC 和 Rt △A' B' C' 中,
能力提升
5. A ∵AB∶BC=3∶4,∴设AB=3x,BC=4x,
∵BD⊥AC,∴∠ADB=∠ABC=90°,
. ∠BAD=∠CAB,∴ △ABD∽△ACB,
∵ AE 平 分 ∠BAC,∴ ∠BAF = ∠DAF, ∴ ∠AEB=∠AFD,
∵ ∠AFD = ∠BFE,∴ ∠BEF = ∠BFE,∴ BE = BF,
∵ ∠ABE = ∠ADF = 90°,∠BAE = ∠DAF,∴ △ABE∽△ADF,
即 BF:FD=5∶3.
6证明 (1)∵ 四边形ABCD 是菱形,∴ AB=BC,AC⊥BD,又∵∠ABC=60°,∴△ABC是等边三角形,∴AB=AC,∵ 点 F 为 BC 的中点,∴ AF⊥BC,∴∠BOC=∠BFE=90°,又∵∠EBF=∠CBO,∴△BEF∽△BCO.
(2)在等边△ABC中,∵ BO⊥AC,AF⊥BC,∴CG⊥AB,∴∠BGE=∠AGE,BG=AG.
在△BEG和△AEG中,
∴△BEG≌△AEG(SAS).
素养提优
7.解析 (1)∵AB=AC,∠BAC=90°,∴∠B=∠C=45°,
∴ ∠BEP = 180° - 45° - ∠BPE = 135° - ∠BPE,
··∠EPF=45°,∴∠CPF=180°-45°-∠BPE=135°-∠BPE,∴∠BEP=∠CPF,
但△BPE与△CFP 不一定全等.
故①错误,②③④正确,故答案为②③④.
(2)△BPE∽△CFP.
理由:∵AB=AC,∠BAC=90°,∴∠B=∠C=45°,
∴∠BEP=180°-45°-∠BPE=135°-∠BPE,
∵ ∠EPF = 45°,∴ ∠CPF = 180°-45°-∠BPE =135°-∠BPE,
∴∠BEP=∠CPF,∴ △BPE∽△CFP.
(3)当点 P为BC 的中点时,△BPE∽△PFE.
理由:如图,连接EF,
∵△BPE∽△CFP,.. BEP=PRp
∵P为BC的中点,∴CP=PB,
∵∠B=∠EPF,∴△BPE∽△PFE.
微专题 “三点定形”证明三角形相似
1 证明 ∵CD∥BE,∴∠DCO=∠E,又∠DOC=∠BOE,∴△OCD∽△OEB,∴ODDBCCE由AD∥BC同理可得 即
解析 (1)证明:∵四边形 ABCD是菱形,BD 是对角线,∴AD=DC,∠ADE=∠CDE,又∵DE=DE,∴△ADE≌△CDE,∴ ∠DAE=∠DCE.
·AD∥BC,∴∠DAE=∠F,
..∠DCE=∠F,∵ ∠FEC=∠CEG,
(2)由(1)知△FEC∽△CEG,
设CG=x,则CF=3x,DG=6-x,
∵AD∥CF,∴△ADG∽△FCG,
解得x=4或x=0(舍去),
∴CF=3x=12.
基础夯实
知识点 相似三角形判定定理的证明
1.「2025山东枣庄市中期中」在△ABC 纸片中,∠ACB=90°,BC=5,AC=7,将该纸片沿虚线剪开,剪下的阴影三角形与原三角形不相似的是 ( )
2.如图,在四边形 ABCD 中, ∠B =∠ACD,AB=6,BC=4,AC=5,CD= ,则AD的长为 .
3.「2024上海中考节选」如图所示,在矩形ABCD中,E为边CD上一点,且AE⊥BD.
求证:
4.我们可以借助两个直角三角形全等的条件,探索两个直角三角形相似的条件.
(1)“对于两个直角三角形,满足一边、一锐角分别相等或两直角边分别相等,这两个直角三角形全 等.”类似 地,可以 得 到“满足 或 的两个直角三角形相似.”
(2)“满足斜边和一条直角边分别相等的两个直角三角形全等.”类似地,可以得到“满足 的两个直角三角形相似.”
(3)如图,在 Rt△ABC 和 Rt△A'B'C'中,∠C = 求证: Rt △ABC ∽Rt△A'B'C'.
5.如图,ARt△ABC中, ∠ABC = 90°, BD ⊥AC,垂足为D,AE平分∠BAC,分别交 BD,BC 于点 F,E.若AB: BC=3:4,则BF:FD为( )
A.5:3 B.5:4 C.4:3 D.2:1
6.如图,在菱形 ABCD 中,∠ABC=60°,对角线 AC 与 BD 相交于点 O,点 F 为BC 的中点,连接AF与BD 相交于点 E,连接CE 并延长交AB于点 G.
(1)证明:△BEF∽△BCO.
(2)证明:△BEG≌△AEG.
7.【问题背景】△ABC 中,AB=AC,∠BAC=90°,P 为BC 上的动点,现将一个含45°角的透明三角尺的45°角的顶点落在点 P 处,使三角尺绕点 P 旋转.
【用数学的眼光观察】(1)如图1,当三角尺的两边分别交 AB、AC 于点 E、F 时,以下结论正确的是
①△BPE≌△CFP;②△BPE∽△CFP;
③∠BEP=∠CPF;
【用数学的思维思考】(2)将三角尺绕点 P 旋转到如图2所示的位置时,三角尺的两边分别交 BA 的延长线、边AC于点 E、F,△BPE 与△CFP 相似吗 请说明理由.
【用数学的语言表达】(3)在(2)的条件下,动点 P运动到什么位置时,△BPE∽△PFE 说明理由.
微专题“三点定形”证明三角形相似
方法指引
1.如图,梯形ABCD中,AD∥BC,AC 与BD 相交于O 点,过点 B 作 BE∥CD交CA 的延长线于点 E.求证:
E
2.如图,在菱形ABCD中,点 G在边 CD上,连接AG 并延长,交 BC 的延长线于点 F,连接BD交AF 于点E,连接CE.
(1)求证:
(2)若 求 CF 的长.
*5相似三角形判定定理的证明
基础夯实
1. D 如图 1,∵ CD ⊥AB 于点 D,.. ∠ADC = 90°,∵ ∠ACB = 90°,∴ ∠ADC = ∠ACB,∵ ∠A = ∠A,∵.△ACD∽△ABC,故A不符合题意;如图2,∵ EF⊥AC,∴∠AFE=90°,∵∠ACB=90°,∴∠AFE=∠ACB,.. EF∥BC,∴ △AEF∽△ABC,故 B 不符合题意;如图3,∵BC=5,AC=7,HC=2.5,GC=3.5,∴HCE=25= ∴△GHC∽△ABC,故 C 不符合题意;如图4,∵BC= KC4C,∴△KLC与△ABC不相似,故D符合题意.故选D.
2答案
解析 ∵AB=6,BC=4,AC=5,CD= ,∴AB=BCAC= 又∵∠B=∠ACD,
∴△ABC∽△DCA,∴∠CD=4B=4/s,
故答案为254.
3.证明 · · 四边形 ABCD 是矩形,∴ ∠BAD = 90°,∠ADE=90°,AB=DC,∴∠ABD+∠ADB=90°,
∵AE⊥BD,∴∠DAE+∠ADB=90°,
∴∠ABD=∠DAE,
∵∠BAD=∠ADE=90°,∴△ADE∽△BAD,
4.解析 (1)一个锐角相等;两直角边成比例.
(2)斜边和一条直角边成比例.
(3)证明:设 则AB=kA'B',AC=kA'C'. 在 Rt △ABC 和 Rt △A' B' C' 中,
能力提升
5. A ∵AB∶BC=3∶4,∴设AB=3x,BC=4x,
∵BD⊥AC,∴∠ADB=∠ABC=90°,
. ∠BAD=∠CAB,∴ △ABD∽△ACB,
∵ AE 平 分 ∠BAC,∴ ∠BAF = ∠DAF, ∴ ∠AEB=∠AFD,
∵ ∠AFD = ∠BFE,∴ ∠BEF = ∠BFE,∴ BE = BF,
∵ ∠ABE = ∠ADF = 90°,∠BAE = ∠DAF,∴ △ABE∽△ADF,
即 BF:FD=5∶3.
6证明 (1)∵ 四边形ABCD 是菱形,∴ AB=BC,AC⊥BD,又∵∠ABC=60°,∴△ABC是等边三角形,∴AB=AC,∵ 点 F 为 BC 的中点,∴ AF⊥BC,∴∠BOC=∠BFE=90°,又∵∠EBF=∠CBO,∴△BEF∽△BCO.
(2)在等边△ABC中,∵ BO⊥AC,AF⊥BC,∴CG⊥AB,∴∠BGE=∠AGE,BG=AG.
在△BEG和△AEG中,
∴△BEG≌△AEG(SAS).
素养提优
7.解析 (1)∵AB=AC,∠BAC=90°,∴∠B=∠C=45°,
∴ ∠BEP = 180° - 45° - ∠BPE = 135° - ∠BPE,
··∠EPF=45°,∴∠CPF=180°-45°-∠BPE=135°-∠BPE,∴∠BEP=∠CPF,
但△BPE与△CFP 不一定全等.
故①错误,②③④正确,故答案为②③④.
(2)△BPE∽△CFP.
理由:∵AB=AC,∠BAC=90°,∴∠B=∠C=45°,
∴∠BEP=180°-45°-∠BPE=135°-∠BPE,
∵ ∠EPF = 45°,∴ ∠CPF = 180°-45°-∠BPE =135°-∠BPE,
∴∠BEP=∠CPF,∴ △BPE∽△CFP.
(3)当点 P为BC 的中点时,△BPE∽△PFE.
理由:如图,连接EF,
∵△BPE∽△CFP,.. BEP=PRp
∵P为BC的中点,∴CP=PB,
∵∠B=∠EPF,∴△BPE∽△PFE.
微专题 “三点定形”证明三角形相似
1 证明 ∵CD∥BE,∴∠DCO=∠E,又∠DOC=∠BOE,∴△OCD∽△OEB,∴ODDBCCE由AD∥BC同理可得 即
解析 (1)证明:∵四边形 ABCD是菱形,BD 是对角线,∴AD=DC,∠ADE=∠CDE,又∵DE=DE,∴△ADE≌△CDE,∴ ∠DAE=∠DCE.
·AD∥BC,∴∠DAE=∠F,
..∠DCE=∠F,∵ ∠FEC=∠CEG,
(2)由(1)知△FEC∽△CEG,
设CG=x,则CF=3x,DG=6-x,
∵AD∥CF,∴△ADG∽△FCG,
解得x=4或x=0(舍去),
∴CF=3x=12.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
