第四章 图形的相似 自主检测 2025-2026学年北师大版数学九年级上册(含答案)
文档属性
| 名称 | 第四章 图形的相似 自主检测 2025-2026学年北师大版数学九年级上册(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 220.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 09:53:18 | ||
图片预览


文档简介
第四章图形的相似自主检测
一、选择题(每小题6分,共42分)
1.「2025山东青岛期末」已知a,b,c,d是成比例线段,其中a=2cm,b=1cm,c=8cm,则线段d的长为( )
A.3c m B.4 cm
C.5cm D.11 cm
2.「2024上海嘉定期末改编」如果5a=3b(a、b都不等于零),那么 的值是 ( )
A. B.
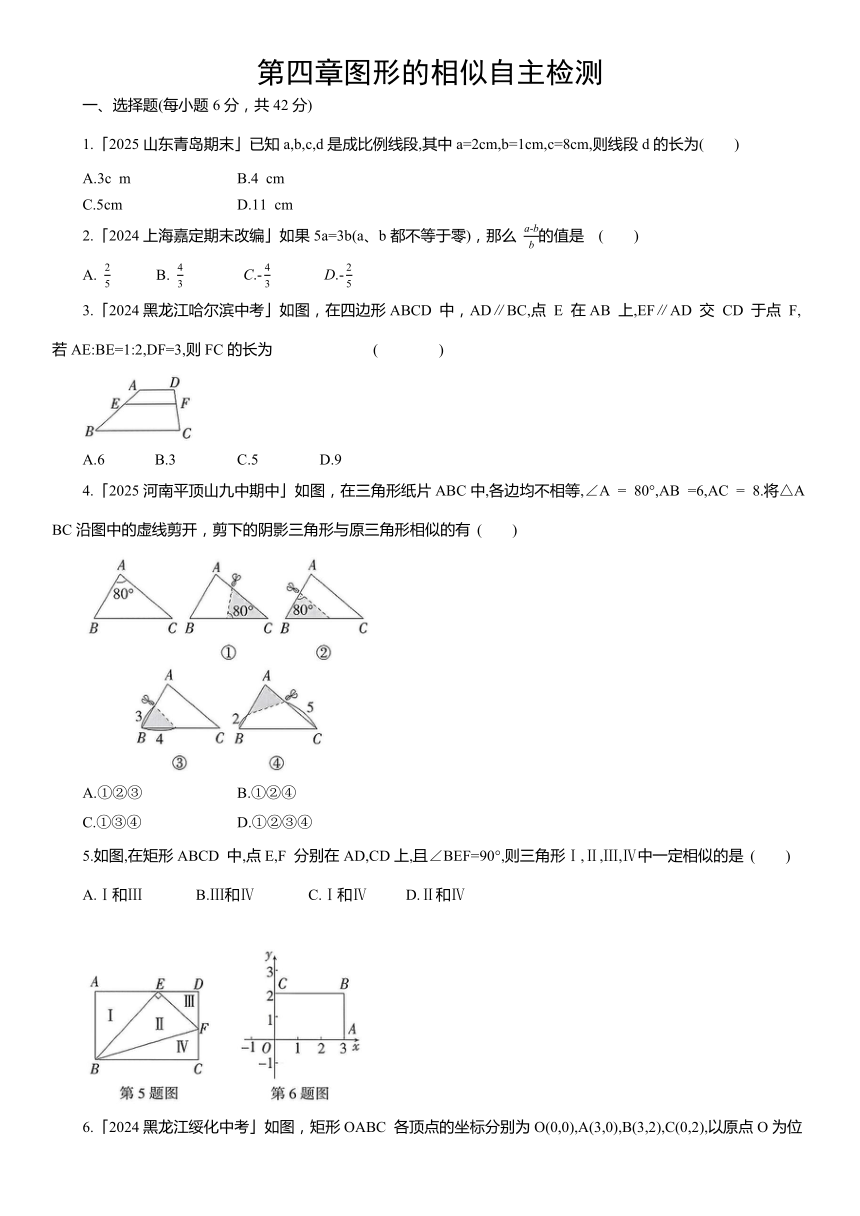
3.「2024黑龙江哈尔滨中考」如图,在四边形ABCD 中,AD∥BC,点 E 在AB 上,EF∥AD 交 CD 于点 F,若AE:BE=1:2,DF=3,则FC的长为 ( )
A.6 B.3 C.5 D.9
4.「2025河南平顶山九中期中」如图,在三角形纸片ABC中,各边均不相等,∠A = 80°,AB =6,AC = 8.将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形相似的有 ( )
A.①②③ B.①②④
C.①③④ D.①②③④
5.如图,在矩形ABCD 中,点E,F 分别在AD,CD上,且∠BEF=90°,则三角形Ⅰ,Ⅱ,Ⅲ,Ⅳ中一定相似的是 ( )
A.Ⅰ和Ⅲ B.Ⅲ和Ⅳ C.Ⅰ和Ⅳ D.Ⅱ和Ⅳ
6.「2024黑龙江绥化中考」如图,矩形OABC 各顶点的坐标分别为O(0,0),A(3,0),B(3,2),C(0,2),以原点O为位似中心,将这个矩形按相似比 缩小,则顶点B 在第一象限对应点的坐标是 ( )
A.(9,4) B.(4,9) C.(1, ) D.(1, )
7.△ABC的边上有D、E、F三点,各点位置如图所示.若∠B=∠FAC,BD=AC,∠BDE=∠C,BE=7,EF=4,FC=5,则四边形ADEF 与△ABC的面积比为( )
A.1∶3 B.1∶4 C.2:5 D.3:8
二、填空题(每小题6分,共18分)
8.「2024青海中考」如图,AC 和BD 相交于点O,请你添加一个条件: ,使得△AOB∽△COD.
9.跨鹊螺鹦鹉螺曲线 「2025安徽蚌埠期中改编」鹦鹉螺曲线的每个半径和后一个半径的比都是黄金比,如图,P是AB的黄金分割点(AP>BP),若线段AB 的长为4 cm,则AP 的长为 cm.
10.「2025上海浦东新区期中」边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为 ,
三、解答题(共40分)
11.「2025浙江杭州绿城育华学校月考」(12分)在6×6的方格纸中,请按下列要求画出格点三角形(顶点均在格点上).
(1)在图1中画出一个以点 C 为位似中心,且与△ABC位似的△CDE(相似比不为1).
(2)在图2中,仅用无刻度直尺(不使用直角)在线段AC上找一点 M,使得
12.(13分)如图,建筑物BC 上有一根旗杆AB,小芳计划测量该建筑物的高度.方法如下:在该建筑物底部所在的平地上有一棵小树FD,小芳沿CD方向后退,发现地面上的点 E、树顶F、旗杆顶端A 恰好在一条直线上,继续后退,发现地面上的点 G、树顶 F、建筑物顶端 B 恰好在一条直线上,已知旗杆AB=3米,FD=4米,DE=5米,EG=1.5米,点A、B、C在一条直线上,AC、FD均垂直于 CG,请你帮助小芳求出这座建筑物的高 BC.
13.(15 分)如图①,△ABC 和△ADE 是等边三角形,连接DC,点F,G,H分别是DE,DC和BC的中点,连接FG,FH.易证:
若△ABC 和△ADE 都是等腰直角三角形,且∠BAC=∠DAE=90°,如图②,若△ABC 和△ADE都是等腰三角形,且∠BAC=∠DAE=120°,如图③,其他条件不变,判断 FH 和 FG 之间的数量关系,写出你的猜想,并利用图②或图③进行证明.
第四章自主检测
1. B ∵a,b,c,d是成比例线段,∴a∶b=c∶d,. a= 故选 B. 故选 D.
3. A ∴在四边形ABCD中,AD∥BC,EF∥AD,∴AD∥EF∥BC,∴∠E=DFC,即 . FC=6,故选A.
4. B①阴影三角形与原三角形有两个角相等,故两三角形相似;
②阴影三角形与原三角形有两个角相等,故两三角形相似;③成比例的两条边的夹角不相等,故两三角形不相似;④两三角形两边成比例且夹角相等,故两三角形相似.故选 B.
5. A ∵ 四边形 ABCD 是矩形,∴ ∠A = ∠D = 90°=∠BEF,∴ ∠ABE +∠AEB = 90°= ∠AEB +∠DEF,∴ ∠ABE=∠DEF,∴ △ABE∽△DEF,故选 A.
6D ∵ 以原点 O 为位似中心,将矩形 OABC 按相似比 缩小,顶点B的坐标为(3,2),∴顶点B 在第一象限对应点的坐标为 即[1, ],故选 D.
7. D ∵ ∠C =∠C,∠CAF =∠B,.. △CAF∽△CBA,∵ACB=CF/ ,∴ CA = CF ·CB,∵ CB=7+4+5=16,.. CA =5×16=80,∴AC>0,∴AC=4 ,∴AC=5/ 16= 易证△BDE≌△ACF, 5):16=3:8,故选 D.
8.答案 ∠A=∠C(答案不唯一)
解析 . ∠AOB=∠COD,∠A=∠C,∴ 根据“两角分别相等的两个三角形相似”证明△AOB∽△COD.
9.答案
解析 ∵ P 是AB 的黄金分割点(AP>BP),AB=4 cm,
10.答案 15
解析 如图,∵ BF ∥DE,∴ △ABF∽ △ADE,
∵ AB=4,AD=4+6+10=20,DE=10,∴ =BF ,
∴BF=2,∴GF=6-2=4,
∵ CK∥DE,∴△ACK∽△ADE,∴∠C=CKE,
∵AC=4+6=10,AD=20,DE=10,∴ =CK,
∴CK=5,∴HK=6-5=1,∴阴影部分的面积=
11.解析 (1)如图1,△CDE 即为所求.
(2)如图2,取格点N,根据网格特点可知AN∥BC,且AN:BC=1:2,连接BN交AC于点 M,此时△ANM∽△CBM,∴ 则点 M 即为所求.
12.解析 由题意可得,∠ACE=∠EDF=90°,∠AEC=∠FED,∴△ACE∽△FDE,
即
由题意可得,∠BCG=∠FDG=90°,∠BGC=∠FGD,
..△BCG∽△FDG,∴BC=CGD,即
..6.5BC=4(CD+6.5),..6.5BC=4×5BC +26,
∴BC=14米,即这座建筑物的高BC为14米.
13.解析 题图②中,
证明:连接AH,CE,AF,如图1,
. △ABC 和△ADE都是等腰直角三角形,且∠BAC=∠DAE=90°,F,H 分别是 DE,BC 的中点,∴AH⊥
∴∠CAH=∠EAF=45°,
∵点F,G分别是DE,DC的中点,
.. CE=2FG,∴FH= FG.
题图③中,FH=FG.
证明:连接AH,CE,AF,如图2,
, △ABC 和△ADE 都是等腰三角形,且∠BAC =∠DAE=120°,
∴ ∠AED=∠ADE=∠ACB=∠B=30°,
点F,H分别是 DE,BC的中点,∴AH⊥BC,AF⊥
点F,G分别是DE,DC的中点,
∴CE=2FG,∴FH=FG.
一、选择题(每小题6分,共42分)
1.「2025山东青岛期末」已知a,b,c,d是成比例线段,其中a=2cm,b=1cm,c=8cm,则线段d的长为( )
A.3c m B.4 cm
C.5cm D.11 cm
2.「2024上海嘉定期末改编」如果5a=3b(a、b都不等于零),那么 的值是 ( )
A. B.
3.「2024黑龙江哈尔滨中考」如图,在四边形ABCD 中,AD∥BC,点 E 在AB 上,EF∥AD 交 CD 于点 F,若AE:BE=1:2,DF=3,则FC的长为 ( )
A.6 B.3 C.5 D.9
4.「2025河南平顶山九中期中」如图,在三角形纸片ABC中,各边均不相等,∠A = 80°,AB =6,AC = 8.将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形相似的有 ( )
A.①②③ B.①②④
C.①③④ D.①②③④
5.如图,在矩形ABCD 中,点E,F 分别在AD,CD上,且∠BEF=90°,则三角形Ⅰ,Ⅱ,Ⅲ,Ⅳ中一定相似的是 ( )
A.Ⅰ和Ⅲ B.Ⅲ和Ⅳ C.Ⅰ和Ⅳ D.Ⅱ和Ⅳ
6.「2024黑龙江绥化中考」如图,矩形OABC 各顶点的坐标分别为O(0,0),A(3,0),B(3,2),C(0,2),以原点O为位似中心,将这个矩形按相似比 缩小,则顶点B 在第一象限对应点的坐标是 ( )
A.(9,4) B.(4,9) C.(1, ) D.(1, )
7.△ABC的边上有D、E、F三点,各点位置如图所示.若∠B=∠FAC,BD=AC,∠BDE=∠C,BE=7,EF=4,FC=5,则四边形ADEF 与△ABC的面积比为( )
A.1∶3 B.1∶4 C.2:5 D.3:8
二、填空题(每小题6分,共18分)
8.「2024青海中考」如图,AC 和BD 相交于点O,请你添加一个条件: ,使得△AOB∽△COD.
9.跨鹊螺鹦鹉螺曲线 「2025安徽蚌埠期中改编」鹦鹉螺曲线的每个半径和后一个半径的比都是黄金比,如图,P是AB的黄金分割点(AP>BP),若线段AB 的长为4 cm,则AP 的长为 cm.
10.「2025上海浦东新区期中」边长分别为10,6,4的三个正方形拼接在一起,它们的底边在同一直线上(如图),则图中阴影部分的面积为 ,
三、解答题(共40分)
11.「2025浙江杭州绿城育华学校月考」(12分)在6×6的方格纸中,请按下列要求画出格点三角形(顶点均在格点上).
(1)在图1中画出一个以点 C 为位似中心,且与△ABC位似的△CDE(相似比不为1).
(2)在图2中,仅用无刻度直尺(不使用直角)在线段AC上找一点 M,使得
12.(13分)如图,建筑物BC 上有一根旗杆AB,小芳计划测量该建筑物的高度.方法如下:在该建筑物底部所在的平地上有一棵小树FD,小芳沿CD方向后退,发现地面上的点 E、树顶F、旗杆顶端A 恰好在一条直线上,继续后退,发现地面上的点 G、树顶 F、建筑物顶端 B 恰好在一条直线上,已知旗杆AB=3米,FD=4米,DE=5米,EG=1.5米,点A、B、C在一条直线上,AC、FD均垂直于 CG,请你帮助小芳求出这座建筑物的高 BC.
13.(15 分)如图①,△ABC 和△ADE 是等边三角形,连接DC,点F,G,H分别是DE,DC和BC的中点,连接FG,FH.易证:
若△ABC 和△ADE 都是等腰直角三角形,且∠BAC=∠DAE=90°,如图②,若△ABC 和△ADE都是等腰三角形,且∠BAC=∠DAE=120°,如图③,其他条件不变,判断 FH 和 FG 之间的数量关系,写出你的猜想,并利用图②或图③进行证明.
第四章自主检测
1. B ∵a,b,c,d是成比例线段,∴a∶b=c∶d,. a= 故选 B. 故选 D.
3. A ∴在四边形ABCD中,AD∥BC,EF∥AD,∴AD∥EF∥BC,∴∠E=DFC,即 . FC=6,故选A.
4. B①阴影三角形与原三角形有两个角相等,故两三角形相似;
②阴影三角形与原三角形有两个角相等,故两三角形相似;③成比例的两条边的夹角不相等,故两三角形不相似;④两三角形两边成比例且夹角相等,故两三角形相似.故选 B.
5. A ∵ 四边形 ABCD 是矩形,∴ ∠A = ∠D = 90°=∠BEF,∴ ∠ABE +∠AEB = 90°= ∠AEB +∠DEF,∴ ∠ABE=∠DEF,∴ △ABE∽△DEF,故选 A.
6D ∵ 以原点 O 为位似中心,将矩形 OABC 按相似比 缩小,顶点B的坐标为(3,2),∴顶点B 在第一象限对应点的坐标为 即[1, ],故选 D.
7. D ∵ ∠C =∠C,∠CAF =∠B,.. △CAF∽△CBA,∵ACB=CF/ ,∴ CA = CF ·CB,∵ CB=7+4+5=16,.. CA =5×16=80,∴AC>0,∴AC=4 ,∴AC=5/ 16= 易证△BDE≌△ACF, 5):16=3:8,故选 D.
8.答案 ∠A=∠C(答案不唯一)
解析 . ∠AOB=∠COD,∠A=∠C,∴ 根据“两角分别相等的两个三角形相似”证明△AOB∽△COD.
9.答案
解析 ∵ P 是AB 的黄金分割点(AP>BP),AB=4 cm,
10.答案 15
解析 如图,∵ BF ∥DE,∴ △ABF∽ △ADE,
∵ AB=4,AD=4+6+10=20,DE=10,∴ =BF ,
∴BF=2,∴GF=6-2=4,
∵ CK∥DE,∴△ACK∽△ADE,∴∠C=CKE,
∵AC=4+6=10,AD=20,DE=10,∴ =CK,
∴CK=5,∴HK=6-5=1,∴阴影部分的面积=
11.解析 (1)如图1,△CDE 即为所求.
(2)如图2,取格点N,根据网格特点可知AN∥BC,且AN:BC=1:2,连接BN交AC于点 M,此时△ANM∽△CBM,∴ 则点 M 即为所求.
12.解析 由题意可得,∠ACE=∠EDF=90°,∠AEC=∠FED,∴△ACE∽△FDE,
即
由题意可得,∠BCG=∠FDG=90°,∠BGC=∠FGD,
..△BCG∽△FDG,∴BC=CGD,即
..6.5BC=4(CD+6.5),..6.5BC=4×5BC +26,
∴BC=14米,即这座建筑物的高BC为14米.
13.解析 题图②中,
证明:连接AH,CE,AF,如图1,
. △ABC 和△ADE都是等腰直角三角形,且∠BAC=∠DAE=90°,F,H 分别是 DE,BC 的中点,∴AH⊥
∴∠CAH=∠EAF=45°,
∵点F,G分别是DE,DC的中点,
.. CE=2FG,∴FH= FG.
题图③中,FH=FG.
证明:连接AH,CE,AF,如图2,
, △ABC 和△ADE 都是等腰三角形,且∠BAC =∠DAE=120°,
∴ ∠AED=∠ADE=∠ACB=∠B=30°,
点F,H分别是 DE,BC的中点,∴AH⊥BC,AF⊥
点F,G分别是DE,DC的中点,
∴CE=2FG,∴FH=FG.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
