1.1 菱形的性质与判定同步练习 (3课时,含答案)2025-2026学年北师大版数学九年级上册
文档属性
| 名称 | 1.1 菱形的性质与判定同步练习 (3课时,含答案)2025-2026学年北师大版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 607.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 21:38:44 | ||
图片预览


文档简介
1.1 菱形的性质与判定
第1课时菱形的性质
基础夯实
知识点 1 菱形的定义
1.如图,在平行四边形ABCD中,AB=4,BC=6,将线段 AB 水平向右平移a(a<6)个单位长度得到线段EF,若四边形 ECDF 为菱形,则a的值为 ( )
A.1 B.2 C.3 D.4
知识点 2 菱形边的性质
2.如图,O是坐标原点,菱形ABOC的顶点B 在x轴的负半轴上,顶点 C 的坐标为(3,4),则顶点A 的坐标为 ( )
A.(-4,2)
C.(-2,4) D.(-4,
3.「2025四川成都铁路中学月考」如图,菱形ABCD 的周长为20,E 是AC 的中点,F 是AB 的中点,连接 EF,则EF=
4.「2024四川广安中考」如图,菱形ABCD 中,点E,F分别是 AB,BC 边上的点,BE =BF,求证:∠DEF=∠DFE.
知识点 3 菱形对角线的性质
5.新课标优秀传统文化 「2025山东青岛市北期中」中国结寓意团圆、美满,以独特的东方神韵体现中国人民的智慧和深厚的文化底蕴.如图,小陶家有一个中国结装饰,可以近似看作菱形ABCD,测得BD=16 cm,AC=12 cm,则此菱形的周长为 ( )
A.28 cm B.40 cm C.56 cm D.80 cm
6.「2025山西大学附中月考」如图,已知在平面直角坐标系中,四边形ABCD 是菱形,其中点B 的坐标是(6,2),点D的坐标是(0,2),点A在x轴上,则点 C的坐标是 ( )
A.(3,2) B.(3,3) C.(3,4) D.(2,4)
7.解释教材变式 如图,四边形ABCD 是菱形,∠ACD=30°,BD=6,求:
(1)∠BAD 和∠ABC 的度数.
(2)AB 和AC 的长.
8.「2024 上海崇明模拟,☆☆」图①是艺术家埃舍尔的作品,他将数学与绘画完美结合,在平面上创造出立体效果.图②是一个菱形,将图②截去一个边长为原来一半的菱形得到图③,用图③镶嵌得到图④,将图④着色后,再次镶嵌便得到图①,则图④中∠ABC的度数是 ( )
A.30° B.45° C.60° D.75°
9.「2025陕西启迪中学月考, 〔公〕如图,在菱形ABCD中,∠ABC=80°,E 是线段 BD 上一动点(点 E 不与点B、D 重合),当△ABE 是等腰三角形时,∠DAE 的度数为 ( )
A.30° B.70°
C.30°或60° D.40°或 70°
10.如图,在菱形ABCD 中,点A、B、C、D 均在坐标轴上,∠ABC=120°,点A(-3,0),点E是CD的中点,点 P 是OC上一动点,则PD+PE 的最小值是 ( )
A.3 B.5
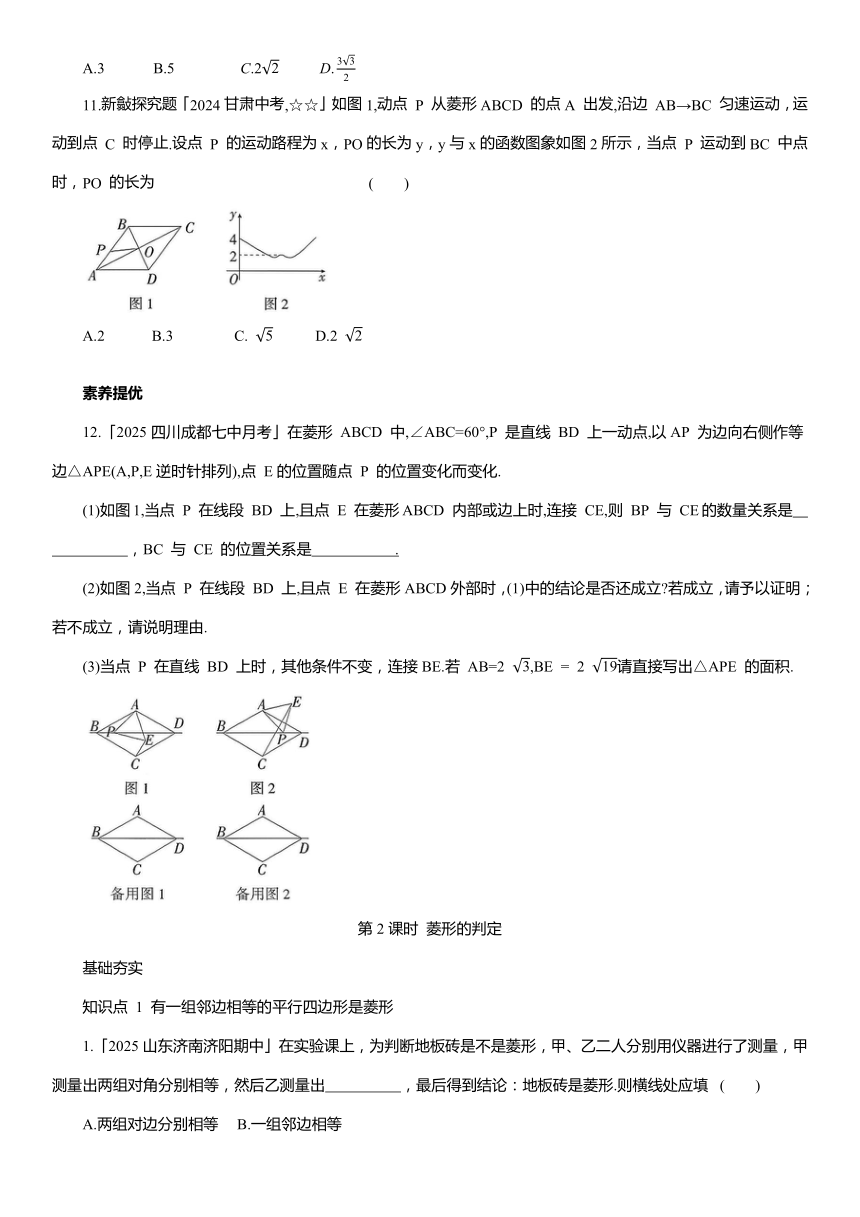
11.新 探究题「2024甘肃中考,☆☆」如图1,动点 P 从菱形ABCD 的点A 出发,沿边 AB→BC 匀速运动,运动到点 C 时停止.设点 P 的运动路程为x,PO的长为y,y与x的函数图象如图2所示,当点 P 运动到BC 中点时,PO 的长为 ( )
A.2 B.3 C. D.2
素养提优
12.「2025四川成都七中月考」在菱形 ABCD 中,∠ABC=60°,P 是直线 BD 上一动点,以AP 为边向右侧作等边△APE(A,P,E逆时针排列),点 E的位置随点 P 的位置变化而变化.
(1)如图1,当点 P 在线段 BD 上,且点 E 在菱形ABCD 内部或边上时,连接 CE,则 BP 与 CE的数量关系是 ,BC 与 CE 的位置关系是 .
(2)如图2,当点 P 在线段 BD 上,且点 E 在菱形ABCD外部时,(1)中的结论是否还成立 若成立,请予以证明;若不成立,请说明理由.
(3)当点 P 在直线 BD 上时,其他条件不变,连接BE.若 AB=2 ,BE = 2 请直接写出△APE 的面积.
菱形的判定
基础夯实
知识点 1 有一组邻边相等的平行四边形是菱形
1.「2025山东济南济阳期中」在实验课上,为判断地板砖是不是菱形,甲、乙二人分别用仪器进行了测量,甲测量出两组对角分别相等,然后乙测量出 ,最后得到结论:地板砖是菱形.则横线处应填 ( )
A.两组对边分别相等 B.一组邻边相等
C.两条对角线相等 D.一组邻角相等
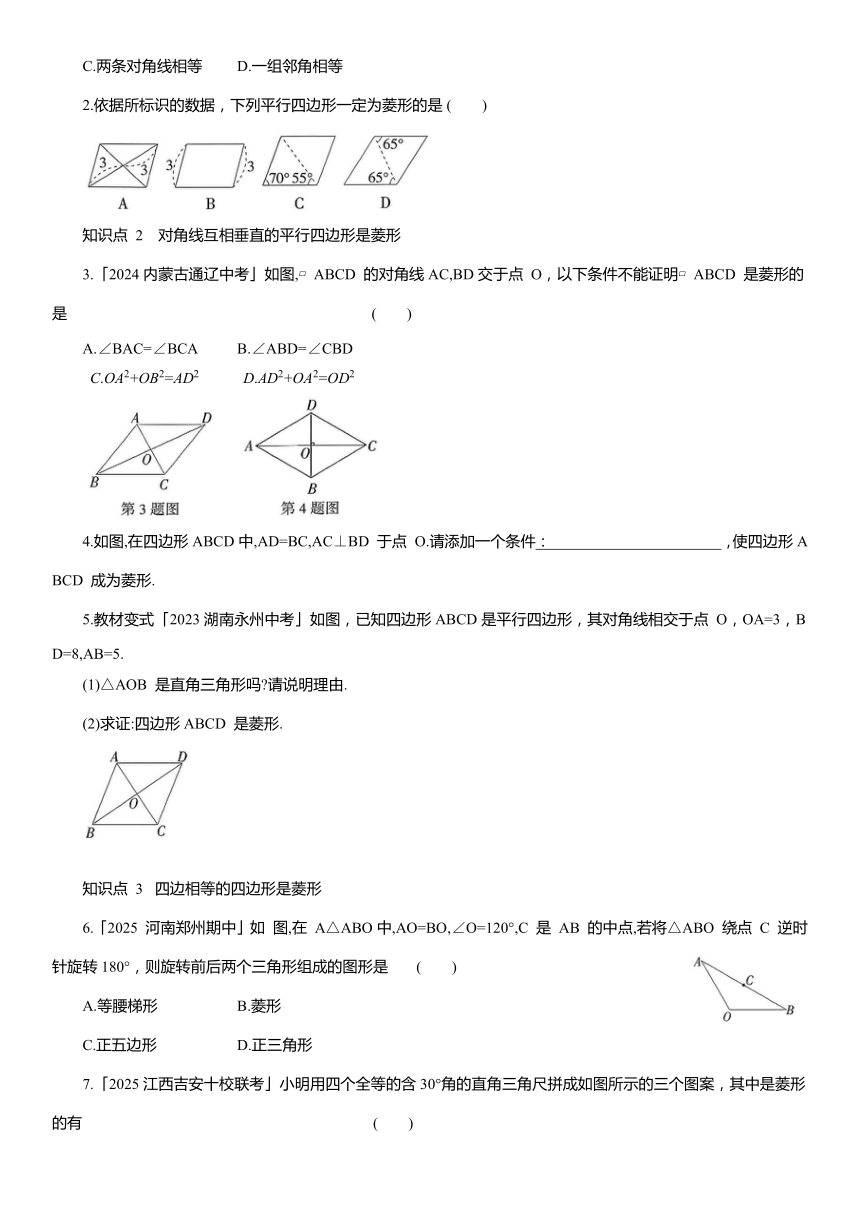
2.依据所标识的数据,下列平行四边形一定为菱形的是 ( )
知识点 2 对角线互相垂直的平行四边形是菱形
3.「2024内蒙古通辽中考」如图, ABCD 的对角线AC,BD交于点 O,以下条件不能证明 ABCD 是菱形的是 ( )
A.∠BAC=∠BCA B.∠ABD=∠CBD
4.如图,在四边形ABCD中,AD=BC,AC⊥BD 于点 O.请添加一个条件: ,使四边形ABCD 成为菱形.
5.教材变式「2023湖南永州中考」如图,已知四边形ABCD是平行四边形,其对角线相交于点 O,OA=3,BD=8,AB=5.
(1)△AOB 是直角三角形吗 请说明理由.
(2)求证:四边形ABCD 是菱形.
知识点 3 四边相等的四边形是菱形
6.「2025 河南郑州期中」如 图,在 A△ABO中,AO=BO,∠O=120°,C 是 AB 的中点,若将△ABO 绕点 C 逆时针旋转180°,则旋转前后两个三角形组成的图形是 ( )
A.等腰梯形 B.菱形
C.正五边形 D.正三角形
7.「2025江西吉安十校联考」小明用四个全等的含30°角的直角三角尺拼成如图所示的三个图案,其中是菱形的有 ( )
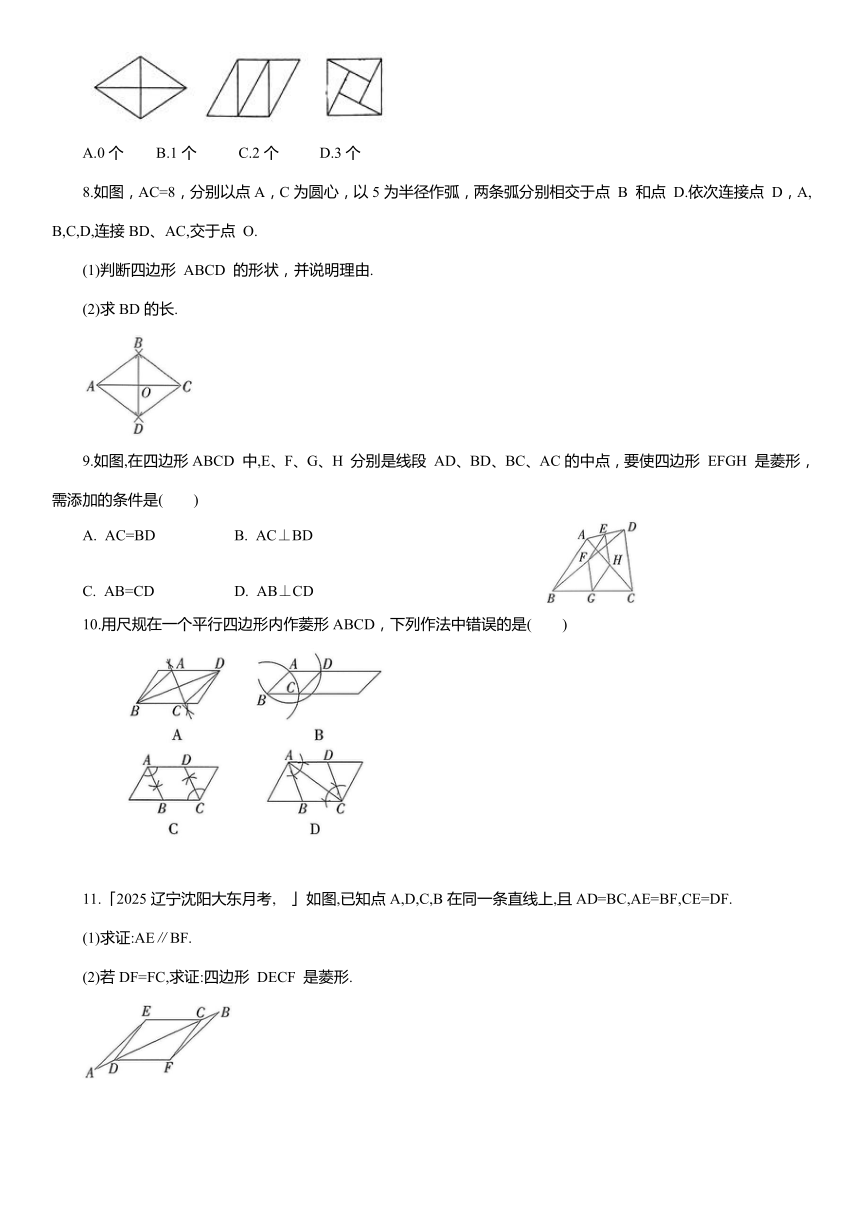
A.0个 B.1个 C.2个 D.3个
8.如图,AC=8,分别以点A,C为圆心,以5为半径作弧,两条弧分别相交于点 B 和点 D.依次连接点 D,A,B,C,D,连接BD、AC,交于点 O.
(1)判断四边形 ABCD 的形状,并说明理由.
(2)求BD的长.
9.如图,在四边形ABCD 中,E、F、G、H 分别是线段 AD、BD、BC、AC的中点,要使四边形 EFGH 是菱形,需添加的条件是( )
A. AC=BD B. AC⊥BD
C. AB=CD D. AB⊥CD
10.用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是( )
11.「2025辽宁沈阳大东月考, 」如图,已知点A,D,C,B在同一条直线上,且AD=BC,AE=BF,CE=DF.
(1)求证:AE∥BF.
(2)若DF=FC,求证:四边形 DECF 是菱形.
12.教材变式做 「2024江苏扬州中考,〔如图1,将两个宽度相等的矩形纸条叠放在一起,得到四边形ABCD.
(1)试判断四边形ABCD 的形状,并说明理由.
(2)已知矩形纸条宽度为2cm ,将矩形纸条旋转至如图2所示的位置时,四边形ABCD 的面积为8 cm ,求此时直线AD、CD 所夹锐角∠1 的度数.
素养提优
13.新根据能力 考虑分类讨论 如图,在平行四边形ABCD中,AB⊥AC,AB=6,BC=10,点 P从点B 出发,沿射线BC方向运动,同时点Q 从点D 出发,沿DA 方向运动,当点 Q 运动到点 A 时,点 Q 停止运动,设运动的时间为 t s.
(1)若点 P 每秒运动3 个单位,点Q 每秒运动1个单位,求当t为何值时,以P、C、D、Q为顶点的四边形为平行四边形.
(2)当点 P 每秒运动 m 个单位,点Q 每秒运动n个单位时,若运动中能使以点 P、C、D、Q为顶点的四边形为菱形,请直接写出 m、n的数量关系.
第3课时 菱形的性质与判定综合
基础夯实
知识点 1 菱形的面积
1.如图,菱形 ABCD 中,AB=10,BD=12,菱形ABCD的面积为 ( )
A.60 B.120 C.192 D.96
2.如图,四边形 ABCD 是菱形,CD=5,BD=8,AE⊥BC于点 E,则AE的长是( )
A. B.6 C.4 D.12
知识点 2 菱形的性质与判定的综合
3.「2025山东青岛期中」如图,在菱形ABCD中,E 是AD的中点,CE,BA的延长线交于点 F,连接AC,DF.
(1)求证:AF=CD.
(2)连接 BD,请判断 BD 与 DF 的位置关系,并说明理由.
(3)当菱形ABCD满足∠ABC= °时,四边形ACDF 是菱形.
4.「2025河南郑州外国语学校期中」如图,在 ABCD 中,点E,F分别在边 BC,AD 上,AC 与 EF 交于点 O,且EF垂直平分AC,连接AE,CF.
(1)求证:四边形AECF 是菱形.
(2)若AC⊥AB,∠B=30°,AE=12,求四边形AECF的面积.
能力提升
5.如图, ABCD的对角线AC,BD 相交于点 O,且 BD =2AB,AE∥BD,OE∥AB.
(1)求证:四边形ABOE 是菱形.
(2)若AO=4,四边形ABOE 的面积是12 ,求 BD的长.
6.如图,已知等边△ABC中,AD⊥BC,E为AB中点.以 D 为圆心,适当长为半径画弧,交DE 于点M,交DB 于点N,分别以M、N为圆心,大于 MV的长为半径画弧,两弧交于点 P,作射线 DP 交AB 于点 G.过点E作EF∥BC 交射线DP 于点 F,连接BF、AF.
(1)求证:四边形 BDEF 是菱形.
(2)若AC=4,求△AFD的面积.
素养提优
7.如图,在边长为 10 的菱形 ABCD 中,对角线 BD=16,对角线AC,BD相交于点 G,点 O 是直线 BD 上的动点,OE⊥AB 于 E,OF⊥AD 于 F.
(1)求对角线AC 的长及菱形ABCD 的面积.
(2)如图①,当点 O 在对角线 BD 上运动时,OE+OF 的值是否发生变化 请说明理由.
(3)如图②,当点 O 在对角线 BD 的延长线上时,OE+OF 的值是否发生变化 若不变,请说明理由;若变化,请探究OE,OF之间的数量关系.
微专题 对角线互相垂直的四边形的面积
例题 如图①,四边形 ABCD 的对角线 则
结论:对角线互相垂直的四边形的面积等于
应用:如图②,四边形 ABCD 是我们常见的风筝的图案,其中对角线 BD 的长为30 cm,AC 的长为40 cm,AC 垂直平分BD,垂足为 E.求四边形 ABCD 的面积.
1 菱形的性质与判定
第1课时 菱形的性质
基础夯实
1. B ∵ 四边形 ABCD 是平行四边形,∴AB∥CD,CE∥FD,CD=AB=4,
∵将线段 AB 水平向右平移得到线段 EF,.. AB∥EF∥CD,∴四边形 ECDF 为平行四边形.根据菱形的定义可知,当CD=CE=4时, ECDF为菱形,此时a=BE=BC-CE=6-4=2.故选 B.
2C 如图,过 C 作 CN⊥x轴于 N,过 A 作 AM⊥x轴于M,
∵点C 的坐标为(3,4),∴ON=3,CN=4,∴OC= 四边形 ABOC 是菱形,∴AC=OC=5,AC∥BO,∴点A的坐标为(-2,4).故选 C.
3.答案
解析 ··菱形 ABCD 的周长为20,∴ BC=20÷4=5,∵E 是AC的中点,F是AB 的中点,∴ EF 是△ABC的中位线,∴ ,故答案为
4.证明 ∵ 四边形ABCD 是菱形,
∴AB=BC=CD=AD,∠A=∠C,
∵BE=BF,∴AB-BE=BC-BF,∴AE=CF,
在△DAE 和△DCF中,
∴ △DAE≌△DCF(SAS),∴ DE=DF,
∴ ∠DEF=∠DFE.
5. B ∵ 四边形ABCD为菱形,且BD=16cm,AC=12cm, 4C=6cm,AC⊥BD,∴∠AOB=90°,在Rt△OAB 中,由勾股定理得
∴菱形ABCD的周长=4AB=4×10=40(cm),故选 B.
6. C 连接AC,BD,相交于点 E,
∵四边形ABCD 是菱形,∴AE=CE,BE=DE,AC⊥BD,
∵点A 在x轴上,点B的坐标为(6,2),点D 的坐标为(0,2),∴BD=6,AE=2,∴DE= BD=3,AC=2AE=4,∴点 C 的坐标为(3,4).故选 C.
7.解析 (1)∵ 四边形ABCD 是菱形,
∴ DC = BC,AC ⊥ BD,∠BCD = 2 ∠ACD,∠ABC =2∠CBD,
∵∠ACD=30°,∴∠BCD=60°,
∴ ∠BAD = ∠BCD = 60°,△BCD 为等边三角形,
∴ ∠CBD=60°,∴∠ABC=2∠CBD=120°.
(2)∵ 四边形 ABCD 是菱形,△BCD 为等边三角形,BD=6,AC⊥BD,∴AO=OC,BC=BD=6,∴AB=BC=CD=6.
在 Rt△COD中,∠ACD=30°,
能力提升
8. C 如图,
∵∠BAD=∠BAE=∠DAE,∠BAD+∠BAE+∠DAE=360°,∴∠BAD=∠BAE=∠DAE=120°,
∵ BC∥AD,∴∠ABC=180°-120°=60°,故选 C.
9. C 在菱形ABCD中,∠ABC=80°,∴ ∠ABD= ∠ABC =40°,∵ AD∥BC,∴∠BAD=180°-∠ABC=100°,
∵△ABE是等腰三角形,点 E不与点 B、D 重合,
∴AE=BE或AB=BE.
当AE=BE时,∠ABE=∠BAE=40°,∴∠DAE=100°- 当AB=BE 时, 40°)=70°,∴∠DAE=100°-70°=30°.
综上所述,当△ABE 是等腰三角形时,∠DAE 的度数为30°或60°,故选 C.
10 A 根据题意得 E 点关于x 轴的对称点是 BC 的中点,设为点 E',连接 DE'交 AC 于点 P,如图,此时PD+PE的值最小,为 DE'的长.
∵四边形ABCD是菱形,∠ABC=120°,点A(-3,0),
∴OA=OC=3,∠DBC=60°,BC=CD,
∴△BCD 是等边三角形,易得 DE'=OC=3,即 PD+PE 的最小值是3.
11 C 结合图象可得,当x=0时,PO=AO=4,当点 P运动到点 B 时,PO=BO=2,∵ 四边形 ABCD 是菱形,∴AC⊥BD,∴ ∠AOB =∠BOC = 90°,∴ AB = BC = .当点 P 运动到BC 中点时,PO 的长为 故选 C.
方法总结 动点与函数图象综合问题的解题策略
(1)趋势判断法:根据几何图形的构造特点,对动点运动进行分段,并判断每段对应函数图象的增减变化趋势;
(2)解析式计算法:根据题意求出每段的函数解析式,结合解析式对应的函数图象进行判断;
(3)定点求值法:结合几何图形特点,在点运动的拐点、垂直点、特殊点处求出函数值,对选项进行排除;
(4)范围排除法:根据动点的运动过程,求出两个变量的变化范围,对选项进行排除.
素养提优
12 解析 (1)如图1,连接AC,延长CE交AD 于点H,
∵四边形ABCD是菱形,∴AB=BC,
∵ ∠ABC=60°,∴ △ABC 是等边三角形,
∴AB=AC,∠BAC=60°.
∵△APE是等边三角形,∴AP=AE,∠PAE=60°,
∵∠BAP+∠PAC=∠CAE+∠PAC=60°,
∴ ∠BAP=∠CAE.
在△BAP 和△CAE中,
∴ △BAP≌△CAE(SAS),∴BP=CE.
∵ 四边形 ABCD 是菱形,.
∵ △ABC是等边三角形,∴∠BCA=60°,
. △BAP≌△CAE,∴∠ABP=∠ACE=30°,
∴∠BCE=∠BCA+∠ACE=60°+30°=90°,∴ CE⊥BC.故答案为 BP=CE;CE⊥BC.
(2)(1)中的结论:BP=CE,CE⊥BC仍然成立,理由如下:如图2,连接AC,
. 在菱形ABCD中,AB=BC,且∠ABC=60°,∴△ABC是等边三角形,∴ AB=AC,∠BAC = ∠ACB = 60°,
∴△APE 是等边三角形,∴AP=AE,∠PAE=60°,
∴∠BAC+∠PAC=∠PAE+∠PAC,∴∠BAP=∠CAE.
在△ABP 和△ACE 中,
△ACE(SAS),∴BP=CE,∠ACE=∠ABP,
, ∠ABP= ∠ABC=30°,∴ ∠ACE=∠ABP=30°,
∵.∠BCE=∠ACE+∠ACB=90°,∴CE⊥BC,
∵(1)中的结论:BP=CE,CE⊥BC 仍然成立.
(3)△APE 的面积为7 或31
详解:如图3,当点 P 在 BD 的延长线上时,连接AC交 BD 于点 O,作 EF⊥AP 于 F,
四边形ABCD 是菱形,∴AC⊥BD,BD平分∠ABC,
与(2)同理可知CE⊥BC,∵BE=2 ,BC=AB=
∵'=CE=8,∴DP=2,∴OP=5,
∵ △APE 是等边三角形,∴ 如图4,当点 P 在 DB 的延长线上时,同理可得AP=
综上所述,△APE的面积为7 或31
第2课时 菱形的判定
基础夯实
1. B由“甲测量出两组对角分别相等”推知该地板砖是平行四边形,则当乙测量出一组邻边相等时,该平行四边形地板砖是菱形,故选 B.
2. C选项 A 中,∵四边形是平行四边形,∴对角线互相平分,故A 不一定是菱形.选项 B 中,∵四边形是平行四边形,∴对边相等,故B 不一定是菱形.选项 C中,根据三角形的内角和定理可得: 55°,..平行四边形的邻边相等,..C是菱形.
选项 D中,∵四边形是平行四边形,∴对边平行,故D不一定是菱形.故选 C.
3. D 选项 A,∵ ∠BAC=∠BCA,∴AB=BC,∴ ABCD是菱形,故选项A不符合题意.选项B,∵四边形ABCD是平行四边形,∴ AD∥BC,∴ ∠ADB = ∠CBD,·∠ABD=∠CBD,.. ∠ABD = ∠ADB,∴ AB =AD,. ABCD是菱形,故选项B不符合题意.选项 C,∵四边形ABCD 是平行四边形, OB=OD,. OA +OB =AD ,∴ OA +OD =AD ,.. ∠AOD=90°,∴ AC⊥BD,∴ ABCD 是菱形,故选项 C 不符合题意.选项 D,. AD +OA =OD ,∴∠OAD=90°,∴OA⊥AD,∴AC与BD不垂直,∴ ABCD不是菱形,故选项D符合题意.故选 D.
4.答案 AD∥BC(答案不唯一)
解析 答案不唯一.当添加“AD∥BC”时,∵AD∥BC,AD=BC,∴四边形ABCD 是平行四边形,∴AC⊥BD,..四边形ABCD 是菱形.
5.解析 (1)△AOB 是直角三角形.理由:∵ 四边形ABCD 是平行四边形, ∵OA=3,AB=5,∴ OA +OB =AB ,∴ △AOB 是直角三角形,且∠AOB=90°.
(2)证明:由(1)可知∠AOB=90°,∴AC⊥BD,∴平行四边形ABCD 是菱形.
6. B 如图,
∵C是AB的中点,∴ CA=CB.△ABO 绕点 C 逆时针旋转180°得到△BAC',· BC'=AO,AC'=BO,∵AO=BO, .四边形 AOBC'为菱形.故选 B.
7 D 四个全等的含 30°角的直角三角尺拼成如题图所示的三个图案,第一个与第三个图案中的四边形的四条边都相等,∴第一个与第三个图案是菱形.第二个图案如图.
∵上图是由四个全等的含30°角的直角三角尺拼成的四边形,∴AD=BC=EF,CD=AB,
··∠ADF=∠FEB=30°,∠AFD=∠FBE=90°,∴AF= 2AD=AD,∴AB=BC=CD=AD,
∴四边形ABCD 是菱形.故选 D.
8解析 (1)四边形ABCD 为菱形.理由如下:由作法,得AB=AD=CB=CD=5,∴四边形ABCD 为菱形.
(2)∵四边形ABCD为菱形,
在 Rt△AOB中,(
能力提升
9. C ∵ 点 E、F、G、H 分别是AD、BD、BC、AC 的中点, ∵ 当 EF = FC=GH=EH时,四边形 EFGH 是菱形,∴当AB=CD时,四边形EFGH 是菱形.故选 C.
10 C 选项 A,由作图可知AC 是 BD 的垂直平分线,. AB=AD,设AC与BD的交点为O,则OB=OD.易知AD∥BC,.. ∠ADO = ∠CBO,又∠AOD = ∠COB,∴△AOD≌△COB,∴AD=BC,∴四边形ABCD 是平行四边形,又AB=AD,∴四边形ABCD 是菱形,不符合题意;选项 B,由作图可知 AB = BC,AD =AB,∴BC=AD,又BC∥AD,∴四边形ABCD 是平行四边形,又AB=BC,∴四边形ABCD是菱形,不符合题意;选项C,由作图可知AB、CD是角平分线,只能得出四边形ABCD 是平行四边形,符合题意;选项D,由作图可知∠DAC=∠CAB,∠DCA =∠ACB,. AD∥BC,..∠DAC = ∠ACB,∴ ∠DAC = ∠CAB = ∠DCA,∴AB∥CD,AD=DC,结合AD∥BC可得四边形 ABCD是菱形,不符合题意.故选 C.
11 证明 (1)∵AD=BC,: AD+CD=BC+CD,∴AC=BD,
∵AE=BF,CE=DF,
∴△AEC≌△BFD(SSS),∴∠A=∠B,∴AE∥BF.
(2)∵ △AEC≌△BFD,∴ ∠ECA=∠FDB,∴EC∥DF,∵EC=DF,∴ 四边形DECF 是平行四边形,∵ DF=FC,∴ 四边形 DECF 是菱形.
12.解析 (1)四边形 ABCD 是菱形,理由如下:如图1,作CH⊥AB,垂足为H,CG⊥AD,垂足为G,∵两个纸条为矩形,∴AB∥CD,AD∥BC,..四边形ABCD 是平行四边形,
∵S ABCD=AB·CH=AD·CG,且CH=CG,∴AB=AD,..四边形ABCD是菱形.
(2)如图2,作AM⊥CD,垂足为M,
且AM=2cm,
∴ CD=4 cm,∴AD=CD=4 cm.
在 Rt△ADM中,AM= AD,∴∠1=30°.
素养提优
13.解析 (1)①如图,当点 P 在线段 BC上时,
DQ=t,PC=10-3t,
∵四边形ABCD 是平行四边形,∴AD∥BC.
若以点 P、C、D、Q为顶点的四边形是平行四边形,则.DQ=PC,∴t=10-3t,.. t=2.5.
②当点 P 在 BC 的延长线上时,PC=3t-10.
若以点 P、C、D、Q为顶点的四边形是平行四边形,则DQ=PC,∴t=3t-10,∴t=5.
综上,当t的值为2.5 或5时,以点 P、C、D、Q 为顶点的四边形为平行四边形.
(2)①当点 P 在线段 BC 上时,若以点 P、C、D、Q 为顶点的四边形是菱形,则DQ=PC=CD=6,∴nt=10-
②如图,当点 P 在 BC 的延长线上时,连接PQ,交 CD于点 E,
·AB⊥AC,∴∠BAC=90°,
四边形ABCD 是平行四边形,
.. CD∥AB,∴∠ACD=∠BAC=90°.
若以点 P、C、D、Q 为顶点的四边形是菱形,则 PQ⊥CD,CE=DE=3,PE=QE,DQ=PC,∴PQ∥AC.
:AD∥BC,∴四边形ACPQ 是平行四边形,
∴PQ=AC=8,∴QE=PE=4,
∴nt= mt-10=5,∴mt=15,∴m=3n.
综上,当3m=2n或m=3n时,以点 P、C、D、Q 为顶点的四边形为菱形.
第3 课时 菱形的性质与判定综合
基础夯实
1. D如图,连接AC,交B D于点O,
∵四边形ABCD 是菱形,∴ BD⊥AC,OA=OC,OB=OD,∵BD=12,∴OB=OD=6.在 Rt△AOB 中,AO=
∴菱形的面积为 故选 D.
2. A ∵ 四边形ABCD 是菱形,CD=5,BD=8, . BC=CD=5,BO=DO=4,OA=OC,AC⊥BD,∴∠BOC=90°.在 Rt△OBC 中,由勾股定理得 -4 =3,∴AC=2OC=6,∵菱形ABCD 的面积=AE ,故选 A.
3.解析 (1)证明;∵四边形 ABCD 是菱形,∴AB∥CD,∴∠AFE=∠DCE,∵E是AD的中点,∴AE=DE,在△AFE与△DCE中, ∴△AFE≌△DCE(AAS),∴AF=CD.
(2)BD⊥DF.理由:如图,
·四边形ABCD 是菱形,∴AB=AD=CD,
AF=CD,∴AB=AD=AF,∴∠ABD=∠ADB,∠ADF= 90°.. BD⊥DF.
(3)当菱形ABCD满足∠ABC=60°时,四边形ACDF是菱形.
提示:∵AF=CD,AF∥CD,∴四边形ACDF 是平行四边形,∵∠ABC=60°,AB=BC,
△ABC是等边三角形,∴AB=AC,∴AC=CD,平行四边形ACDF 是菱形.
4.解析 (1)证明:··四边形 ABCD 是平行四边形,
∴AD∥BC,..∠OAF=∠OCE,
∵EF 垂直平分AC,∴EF⊥AC,OA=OC,在△AOF和△COE中.
∴△AOF≌△COE(ASA),
∴OE=OF,∴ 四边形AECF 是平行四边形,
又∵EF⊥AC,∴平行四边形AECF是菱形.
(2)由(1)知,OE=OF,四边形 AECF 是菱形,∴CE=AE=12.
∵ AC ⊥AB,EF ⊥AC,∴ ∠COE = 90°,EF ∥AB,
∴EF=2OE=12 ,.. 菱形 AECF 的面积
能力提升
5.解析 (1)证明:∵四边形ABCD 是平行四边形,OB=OD= BD,∵BD=2AB,∴AB=OB,∵AE∥BD,OE∥AB,∴四边形ABOE 是平行四边形,又∵AB=OB,∴平行四边形ABOE 是菱形.
(2)如图,连接BE,交 OA 于 F,∵四边形ABOE是菱形,∴OA⊥ B BE = 2BE, .. BE = 6 , . . BF = 3 ,.. OB = ,即 BD 的长为
6.解析 (1)证明:∵ △ABC 是等边三角形,∴AB=BC,∠ABC=60°,
E 为AB 中点,..BE= AB,.. BE=BD,
.△BED是等边三角形,∴BE=BD=DE,
由作图知,DF平分∠EDB,∴∠EDF=∠FDB,
·· EF∥BC,. ∠EFD =∠FDB, . ∠EFD =∠EDF,. EF=ED,∴ EF=BD,..四边形BDEF 是菱形.
(2)∵ △ABC是等边三角形,AD⊥BC,
∴∠C=60°,∠ADC=90°,∠CAD=∠BAD=30°,
四边形 BDEF 是菱形,∴AG⊥FD,FG=GD.
在 Rt△AGD 中,∵
7.解析 (1)在菱形ABCD中, 16=8,
由勾股定理得 12,∴菱形ABCD 的面积
(2)不发生变化.理由:如图①,连接AO,则 即
∴OE+OF=9.6,
故OE+OF 的值不发生变化.
(3)发生变化.
如图②,连接AO,则
即
.. OE-OF=9.6,
.. OE+OF的值发生变化,OE、OF 之间的数量关系为OE-OF=9.6.
微专题 对角线互相垂直的四边形的面积例题 解析 结论:两对角线乘积的一半.
应用:
第1课时菱形的性质
基础夯实
知识点 1 菱形的定义
1.如图,在平行四边形ABCD中,AB=4,BC=6,将线段 AB 水平向右平移a(a<6)个单位长度得到线段EF,若四边形 ECDF 为菱形,则a的值为 ( )
A.1 B.2 C.3 D.4
知识点 2 菱形边的性质
2.如图,O是坐标原点,菱形ABOC的顶点B 在x轴的负半轴上,顶点 C 的坐标为(3,4),则顶点A 的坐标为 ( )
A.(-4,2)
C.(-2,4) D.(-4,
3.「2025四川成都铁路中学月考」如图,菱形ABCD 的周长为20,E 是AC 的中点,F 是AB 的中点,连接 EF,则EF=
4.「2024四川广安中考」如图,菱形ABCD 中,点E,F分别是 AB,BC 边上的点,BE =BF,求证:∠DEF=∠DFE.
知识点 3 菱形对角线的性质
5.新课标优秀传统文化 「2025山东青岛市北期中」中国结寓意团圆、美满,以独特的东方神韵体现中国人民的智慧和深厚的文化底蕴.如图,小陶家有一个中国结装饰,可以近似看作菱形ABCD,测得BD=16 cm,AC=12 cm,则此菱形的周长为 ( )
A.28 cm B.40 cm C.56 cm D.80 cm
6.「2025山西大学附中月考」如图,已知在平面直角坐标系中,四边形ABCD 是菱形,其中点B 的坐标是(6,2),点D的坐标是(0,2),点A在x轴上,则点 C的坐标是 ( )
A.(3,2) B.(3,3) C.(3,4) D.(2,4)
7.解释教材变式 如图,四边形ABCD 是菱形,∠ACD=30°,BD=6,求:
(1)∠BAD 和∠ABC 的度数.
(2)AB 和AC 的长.
8.「2024 上海崇明模拟,☆☆」图①是艺术家埃舍尔的作品,他将数学与绘画完美结合,在平面上创造出立体效果.图②是一个菱形,将图②截去一个边长为原来一半的菱形得到图③,用图③镶嵌得到图④,将图④着色后,再次镶嵌便得到图①,则图④中∠ABC的度数是 ( )
A.30° B.45° C.60° D.75°
9.「2025陕西启迪中学月考, 〔公〕如图,在菱形ABCD中,∠ABC=80°,E 是线段 BD 上一动点(点 E 不与点B、D 重合),当△ABE 是等腰三角形时,∠DAE 的度数为 ( )
A.30° B.70°
C.30°或60° D.40°或 70°
10.如图,在菱形ABCD 中,点A、B、C、D 均在坐标轴上,∠ABC=120°,点A(-3,0),点E是CD的中点,点 P 是OC上一动点,则PD+PE 的最小值是 ( )
A.3 B.5
11.新 探究题「2024甘肃中考,☆☆」如图1,动点 P 从菱形ABCD 的点A 出发,沿边 AB→BC 匀速运动,运动到点 C 时停止.设点 P 的运动路程为x,PO的长为y,y与x的函数图象如图2所示,当点 P 运动到BC 中点时,PO 的长为 ( )
A.2 B.3 C. D.2
素养提优
12.「2025四川成都七中月考」在菱形 ABCD 中,∠ABC=60°,P 是直线 BD 上一动点,以AP 为边向右侧作等边△APE(A,P,E逆时针排列),点 E的位置随点 P 的位置变化而变化.
(1)如图1,当点 P 在线段 BD 上,且点 E 在菱形ABCD 内部或边上时,连接 CE,则 BP 与 CE的数量关系是 ,BC 与 CE 的位置关系是 .
(2)如图2,当点 P 在线段 BD 上,且点 E 在菱形ABCD外部时,(1)中的结论是否还成立 若成立,请予以证明;若不成立,请说明理由.
(3)当点 P 在直线 BD 上时,其他条件不变,连接BE.若 AB=2 ,BE = 2 请直接写出△APE 的面积.
菱形的判定
基础夯实
知识点 1 有一组邻边相等的平行四边形是菱形
1.「2025山东济南济阳期中」在实验课上,为判断地板砖是不是菱形,甲、乙二人分别用仪器进行了测量,甲测量出两组对角分别相等,然后乙测量出 ,最后得到结论:地板砖是菱形.则横线处应填 ( )
A.两组对边分别相等 B.一组邻边相等
C.两条对角线相等 D.一组邻角相等
2.依据所标识的数据,下列平行四边形一定为菱形的是 ( )
知识点 2 对角线互相垂直的平行四边形是菱形
3.「2024内蒙古通辽中考」如图, ABCD 的对角线AC,BD交于点 O,以下条件不能证明 ABCD 是菱形的是 ( )
A.∠BAC=∠BCA B.∠ABD=∠CBD
4.如图,在四边形ABCD中,AD=BC,AC⊥BD 于点 O.请添加一个条件: ,使四边形ABCD 成为菱形.
5.教材变式「2023湖南永州中考」如图,已知四边形ABCD是平行四边形,其对角线相交于点 O,OA=3,BD=8,AB=5.
(1)△AOB 是直角三角形吗 请说明理由.
(2)求证:四边形ABCD 是菱形.
知识点 3 四边相等的四边形是菱形
6.「2025 河南郑州期中」如 图,在 A△ABO中,AO=BO,∠O=120°,C 是 AB 的中点,若将△ABO 绕点 C 逆时针旋转180°,则旋转前后两个三角形组成的图形是 ( )
A.等腰梯形 B.菱形
C.正五边形 D.正三角形
7.「2025江西吉安十校联考」小明用四个全等的含30°角的直角三角尺拼成如图所示的三个图案,其中是菱形的有 ( )
A.0个 B.1个 C.2个 D.3个
8.如图,AC=8,分别以点A,C为圆心,以5为半径作弧,两条弧分别相交于点 B 和点 D.依次连接点 D,A,B,C,D,连接BD、AC,交于点 O.
(1)判断四边形 ABCD 的形状,并说明理由.
(2)求BD的长.
9.如图,在四边形ABCD 中,E、F、G、H 分别是线段 AD、BD、BC、AC的中点,要使四边形 EFGH 是菱形,需添加的条件是( )
A. AC=BD B. AC⊥BD
C. AB=CD D. AB⊥CD
10.用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是( )
11.「2025辽宁沈阳大东月考, 」如图,已知点A,D,C,B在同一条直线上,且AD=BC,AE=BF,CE=DF.
(1)求证:AE∥BF.
(2)若DF=FC,求证:四边形 DECF 是菱形.
12.教材变式做 「2024江苏扬州中考,〔如图1,将两个宽度相等的矩形纸条叠放在一起,得到四边形ABCD.
(1)试判断四边形ABCD 的形状,并说明理由.
(2)已知矩形纸条宽度为2cm ,将矩形纸条旋转至如图2所示的位置时,四边形ABCD 的面积为8 cm ,求此时直线AD、CD 所夹锐角∠1 的度数.
素养提优
13.新根据能力 考虑分类讨论 如图,在平行四边形ABCD中,AB⊥AC,AB=6,BC=10,点 P从点B 出发,沿射线BC方向运动,同时点Q 从点D 出发,沿DA 方向运动,当点 Q 运动到点 A 时,点 Q 停止运动,设运动的时间为 t s.
(1)若点 P 每秒运动3 个单位,点Q 每秒运动1个单位,求当t为何值时,以P、C、D、Q为顶点的四边形为平行四边形.
(2)当点 P 每秒运动 m 个单位,点Q 每秒运动n个单位时,若运动中能使以点 P、C、D、Q为顶点的四边形为菱形,请直接写出 m、n的数量关系.
第3课时 菱形的性质与判定综合
基础夯实
知识点 1 菱形的面积
1.如图,菱形 ABCD 中,AB=10,BD=12,菱形ABCD的面积为 ( )
A.60 B.120 C.192 D.96
2.如图,四边形 ABCD 是菱形,CD=5,BD=8,AE⊥BC于点 E,则AE的长是( )
A. B.6 C.4 D.12
知识点 2 菱形的性质与判定的综合
3.「2025山东青岛期中」如图,在菱形ABCD中,E 是AD的中点,CE,BA的延长线交于点 F,连接AC,DF.
(1)求证:AF=CD.
(2)连接 BD,请判断 BD 与 DF 的位置关系,并说明理由.
(3)当菱形ABCD满足∠ABC= °时,四边形ACDF 是菱形.
4.「2025河南郑州外国语学校期中」如图,在 ABCD 中,点E,F分别在边 BC,AD 上,AC 与 EF 交于点 O,且EF垂直平分AC,连接AE,CF.
(1)求证:四边形AECF 是菱形.
(2)若AC⊥AB,∠B=30°,AE=12,求四边形AECF的面积.
能力提升
5.如图, ABCD的对角线AC,BD 相交于点 O,且 BD =2AB,AE∥BD,OE∥AB.
(1)求证:四边形ABOE 是菱形.
(2)若AO=4,四边形ABOE 的面积是12 ,求 BD的长.
6.如图,已知等边△ABC中,AD⊥BC,E为AB中点.以 D 为圆心,适当长为半径画弧,交DE 于点M,交DB 于点N,分别以M、N为圆心,大于 MV的长为半径画弧,两弧交于点 P,作射线 DP 交AB 于点 G.过点E作EF∥BC 交射线DP 于点 F,连接BF、AF.
(1)求证:四边形 BDEF 是菱形.
(2)若AC=4,求△AFD的面积.
素养提优
7.如图,在边长为 10 的菱形 ABCD 中,对角线 BD=16,对角线AC,BD相交于点 G,点 O 是直线 BD 上的动点,OE⊥AB 于 E,OF⊥AD 于 F.
(1)求对角线AC 的长及菱形ABCD 的面积.
(2)如图①,当点 O 在对角线 BD 上运动时,OE+OF 的值是否发生变化 请说明理由.
(3)如图②,当点 O 在对角线 BD 的延长线上时,OE+OF 的值是否发生变化 若不变,请说明理由;若变化,请探究OE,OF之间的数量关系.
微专题 对角线互相垂直的四边形的面积
例题 如图①,四边形 ABCD 的对角线 则
结论:对角线互相垂直的四边形的面积等于
应用:如图②,四边形 ABCD 是我们常见的风筝的图案,其中对角线 BD 的长为30 cm,AC 的长为40 cm,AC 垂直平分BD,垂足为 E.求四边形 ABCD 的面积.
1 菱形的性质与判定
第1课时 菱形的性质
基础夯实
1. B ∵ 四边形 ABCD 是平行四边形,∴AB∥CD,CE∥FD,CD=AB=4,
∵将线段 AB 水平向右平移得到线段 EF,.. AB∥EF∥CD,∴四边形 ECDF 为平行四边形.根据菱形的定义可知,当CD=CE=4时, ECDF为菱形,此时a=BE=BC-CE=6-4=2.故选 B.
2C 如图,过 C 作 CN⊥x轴于 N,过 A 作 AM⊥x轴于M,
∵点C 的坐标为(3,4),∴ON=3,CN=4,∴OC= 四边形 ABOC 是菱形,∴AC=OC=5,AC∥BO,∴点A的坐标为(-2,4).故选 C.
3.答案
解析 ··菱形 ABCD 的周长为20,∴ BC=20÷4=5,∵E 是AC的中点,F是AB 的中点,∴ EF 是△ABC的中位线,∴ ,故答案为
4.证明 ∵ 四边形ABCD 是菱形,
∴AB=BC=CD=AD,∠A=∠C,
∵BE=BF,∴AB-BE=BC-BF,∴AE=CF,
在△DAE 和△DCF中,
∴ △DAE≌△DCF(SAS),∴ DE=DF,
∴ ∠DEF=∠DFE.
5. B ∵ 四边形ABCD为菱形,且BD=16cm,AC=12cm, 4C=6cm,AC⊥BD,∴∠AOB=90°,在Rt△OAB 中,由勾股定理得
∴菱形ABCD的周长=4AB=4×10=40(cm),故选 B.
6. C 连接AC,BD,相交于点 E,
∵四边形ABCD 是菱形,∴AE=CE,BE=DE,AC⊥BD,
∵点A 在x轴上,点B的坐标为(6,2),点D 的坐标为(0,2),∴BD=6,AE=2,∴DE= BD=3,AC=2AE=4,∴点 C 的坐标为(3,4).故选 C.
7.解析 (1)∵ 四边形ABCD 是菱形,
∴ DC = BC,AC ⊥ BD,∠BCD = 2 ∠ACD,∠ABC =2∠CBD,
∵∠ACD=30°,∴∠BCD=60°,
∴ ∠BAD = ∠BCD = 60°,△BCD 为等边三角形,
∴ ∠CBD=60°,∴∠ABC=2∠CBD=120°.
(2)∵ 四边形 ABCD 是菱形,△BCD 为等边三角形,BD=6,AC⊥BD,∴AO=OC,BC=BD=6,∴AB=BC=CD=6.
在 Rt△COD中,∠ACD=30°,
能力提升
8. C 如图,
∵∠BAD=∠BAE=∠DAE,∠BAD+∠BAE+∠DAE=360°,∴∠BAD=∠BAE=∠DAE=120°,
∵ BC∥AD,∴∠ABC=180°-120°=60°,故选 C.
9. C 在菱形ABCD中,∠ABC=80°,∴ ∠ABD= ∠ABC =40°,∵ AD∥BC,∴∠BAD=180°-∠ABC=100°,
∵△ABE是等腰三角形,点 E不与点 B、D 重合,
∴AE=BE或AB=BE.
当AE=BE时,∠ABE=∠BAE=40°,∴∠DAE=100°- 当AB=BE 时, 40°)=70°,∴∠DAE=100°-70°=30°.
综上所述,当△ABE 是等腰三角形时,∠DAE 的度数为30°或60°,故选 C.
10 A 根据题意得 E 点关于x 轴的对称点是 BC 的中点,设为点 E',连接 DE'交 AC 于点 P,如图,此时PD+PE的值最小,为 DE'的长.
∵四边形ABCD是菱形,∠ABC=120°,点A(-3,0),
∴OA=OC=3,∠DBC=60°,BC=CD,
∴△BCD 是等边三角形,易得 DE'=OC=3,即 PD+PE 的最小值是3.
11 C 结合图象可得,当x=0时,PO=AO=4,当点 P运动到点 B 时,PO=BO=2,∵ 四边形 ABCD 是菱形,∴AC⊥BD,∴ ∠AOB =∠BOC = 90°,∴ AB = BC = .当点 P 运动到BC 中点时,PO 的长为 故选 C.
方法总结 动点与函数图象综合问题的解题策略
(1)趋势判断法:根据几何图形的构造特点,对动点运动进行分段,并判断每段对应函数图象的增减变化趋势;
(2)解析式计算法:根据题意求出每段的函数解析式,结合解析式对应的函数图象进行判断;
(3)定点求值法:结合几何图形特点,在点运动的拐点、垂直点、特殊点处求出函数值,对选项进行排除;
(4)范围排除法:根据动点的运动过程,求出两个变量的变化范围,对选项进行排除.
素养提优
12 解析 (1)如图1,连接AC,延长CE交AD 于点H,
∵四边形ABCD是菱形,∴AB=BC,
∵ ∠ABC=60°,∴ △ABC 是等边三角形,
∴AB=AC,∠BAC=60°.
∵△APE是等边三角形,∴AP=AE,∠PAE=60°,
∵∠BAP+∠PAC=∠CAE+∠PAC=60°,
∴ ∠BAP=∠CAE.
在△BAP 和△CAE中,
∴ △BAP≌△CAE(SAS),∴BP=CE.
∵ 四边形 ABCD 是菱形,.
∵ △ABC是等边三角形,∴∠BCA=60°,
. △BAP≌△CAE,∴∠ABP=∠ACE=30°,
∴∠BCE=∠BCA+∠ACE=60°+30°=90°,∴ CE⊥BC.故答案为 BP=CE;CE⊥BC.
(2)(1)中的结论:BP=CE,CE⊥BC仍然成立,理由如下:如图2,连接AC,
. 在菱形ABCD中,AB=BC,且∠ABC=60°,∴△ABC是等边三角形,∴ AB=AC,∠BAC = ∠ACB = 60°,
∴△APE 是等边三角形,∴AP=AE,∠PAE=60°,
∴∠BAC+∠PAC=∠PAE+∠PAC,∴∠BAP=∠CAE.
在△ABP 和△ACE 中,
△ACE(SAS),∴BP=CE,∠ACE=∠ABP,
, ∠ABP= ∠ABC=30°,∴ ∠ACE=∠ABP=30°,
∵.∠BCE=∠ACE+∠ACB=90°,∴CE⊥BC,
∵(1)中的结论:BP=CE,CE⊥BC 仍然成立.
(3)△APE 的面积为7 或31
详解:如图3,当点 P 在 BD 的延长线上时,连接AC交 BD 于点 O,作 EF⊥AP 于 F,
四边形ABCD 是菱形,∴AC⊥BD,BD平分∠ABC,
与(2)同理可知CE⊥BC,∵BE=2 ,BC=AB=
∵'=CE=8,∴DP=2,∴OP=5,
∵ △APE 是等边三角形,∴ 如图4,当点 P 在 DB 的延长线上时,同理可得AP=
综上所述,△APE的面积为7 或31
第2课时 菱形的判定
基础夯实
1. B由“甲测量出两组对角分别相等”推知该地板砖是平行四边形,则当乙测量出一组邻边相等时,该平行四边形地板砖是菱形,故选 B.
2. C选项 A 中,∵四边形是平行四边形,∴对角线互相平分,故A 不一定是菱形.选项 B 中,∵四边形是平行四边形,∴对边相等,故B 不一定是菱形.选项 C中,根据三角形的内角和定理可得: 55°,..平行四边形的邻边相等,..C是菱形.
选项 D中,∵四边形是平行四边形,∴对边平行,故D不一定是菱形.故选 C.
3. D 选项 A,∵ ∠BAC=∠BCA,∴AB=BC,∴ ABCD是菱形,故选项A不符合题意.选项B,∵四边形ABCD是平行四边形,∴ AD∥BC,∴ ∠ADB = ∠CBD,·∠ABD=∠CBD,.. ∠ABD = ∠ADB,∴ AB =AD,. ABCD是菱形,故选项B不符合题意.选项 C,∵四边形ABCD 是平行四边形, OB=OD,. OA +OB =AD ,∴ OA +OD =AD ,.. ∠AOD=90°,∴ AC⊥BD,∴ ABCD 是菱形,故选项 C 不符合题意.选项 D,. AD +OA =OD ,∴∠OAD=90°,∴OA⊥AD,∴AC与BD不垂直,∴ ABCD不是菱形,故选项D符合题意.故选 D.
4.答案 AD∥BC(答案不唯一)
解析 答案不唯一.当添加“AD∥BC”时,∵AD∥BC,AD=BC,∴四边形ABCD 是平行四边形,∴AC⊥BD,..四边形ABCD 是菱形.
5.解析 (1)△AOB 是直角三角形.理由:∵ 四边形ABCD 是平行四边形, ∵OA=3,AB=5,∴ OA +OB =AB ,∴ △AOB 是直角三角形,且∠AOB=90°.
(2)证明:由(1)可知∠AOB=90°,∴AC⊥BD,∴平行四边形ABCD 是菱形.
6. B 如图,
∵C是AB的中点,∴ CA=CB.△ABO 绕点 C 逆时针旋转180°得到△BAC',· BC'=AO,AC'=BO,∵AO=BO, .四边形 AOBC'为菱形.故选 B.
7 D 四个全等的含 30°角的直角三角尺拼成如题图所示的三个图案,第一个与第三个图案中的四边形的四条边都相等,∴第一个与第三个图案是菱形.第二个图案如图.
∵上图是由四个全等的含30°角的直角三角尺拼成的四边形,∴AD=BC=EF,CD=AB,
··∠ADF=∠FEB=30°,∠AFD=∠FBE=90°,∴AF= 2AD=AD,∴AB=BC=CD=AD,
∴四边形ABCD 是菱形.故选 D.
8解析 (1)四边形ABCD 为菱形.理由如下:由作法,得AB=AD=CB=CD=5,∴四边形ABCD 为菱形.
(2)∵四边形ABCD为菱形,
在 Rt△AOB中,(
能力提升
9. C ∵ 点 E、F、G、H 分别是AD、BD、BC、AC 的中点, ∵ 当 EF = FC=GH=EH时,四边形 EFGH 是菱形,∴当AB=CD时,四边形EFGH 是菱形.故选 C.
10 C 选项 A,由作图可知AC 是 BD 的垂直平分线,. AB=AD,设AC与BD的交点为O,则OB=OD.易知AD∥BC,.. ∠ADO = ∠CBO,又∠AOD = ∠COB,∴△AOD≌△COB,∴AD=BC,∴四边形ABCD 是平行四边形,又AB=AD,∴四边形ABCD 是菱形,不符合题意;选项 B,由作图可知 AB = BC,AD =AB,∴BC=AD,又BC∥AD,∴四边形ABCD 是平行四边形,又AB=BC,∴四边形ABCD是菱形,不符合题意;选项C,由作图可知AB、CD是角平分线,只能得出四边形ABCD 是平行四边形,符合题意;选项D,由作图可知∠DAC=∠CAB,∠DCA =∠ACB,. AD∥BC,..∠DAC = ∠ACB,∴ ∠DAC = ∠CAB = ∠DCA,∴AB∥CD,AD=DC,结合AD∥BC可得四边形 ABCD是菱形,不符合题意.故选 C.
11 证明 (1)∵AD=BC,: AD+CD=BC+CD,∴AC=BD,
∵AE=BF,CE=DF,
∴△AEC≌△BFD(SSS),∴∠A=∠B,∴AE∥BF.
(2)∵ △AEC≌△BFD,∴ ∠ECA=∠FDB,∴EC∥DF,∵EC=DF,∴ 四边形DECF 是平行四边形,∵ DF=FC,∴ 四边形 DECF 是菱形.
12.解析 (1)四边形 ABCD 是菱形,理由如下:如图1,作CH⊥AB,垂足为H,CG⊥AD,垂足为G,∵两个纸条为矩形,∴AB∥CD,AD∥BC,..四边形ABCD 是平行四边形,
∵S ABCD=AB·CH=AD·CG,且CH=CG,∴AB=AD,..四边形ABCD是菱形.
(2)如图2,作AM⊥CD,垂足为M,
且AM=2cm,
∴ CD=4 cm,∴AD=CD=4 cm.
在 Rt△ADM中,AM= AD,∴∠1=30°.
素养提优
13.解析 (1)①如图,当点 P 在线段 BC上时,
DQ=t,PC=10-3t,
∵四边形ABCD 是平行四边形,∴AD∥BC.
若以点 P、C、D、Q为顶点的四边形是平行四边形,则.DQ=PC,∴t=10-3t,.. t=2.5.
②当点 P 在 BC 的延长线上时,PC=3t-10.
若以点 P、C、D、Q为顶点的四边形是平行四边形,则DQ=PC,∴t=3t-10,∴t=5.
综上,当t的值为2.5 或5时,以点 P、C、D、Q 为顶点的四边形为平行四边形.
(2)①当点 P 在线段 BC 上时,若以点 P、C、D、Q 为顶点的四边形是菱形,则DQ=PC=CD=6,∴nt=10-
②如图,当点 P 在 BC 的延长线上时,连接PQ,交 CD于点 E,
·AB⊥AC,∴∠BAC=90°,
四边形ABCD 是平行四边形,
.. CD∥AB,∴∠ACD=∠BAC=90°.
若以点 P、C、D、Q 为顶点的四边形是菱形,则 PQ⊥CD,CE=DE=3,PE=QE,DQ=PC,∴PQ∥AC.
:AD∥BC,∴四边形ACPQ 是平行四边形,
∴PQ=AC=8,∴QE=PE=4,
∴nt= mt-10=5,∴mt=15,∴m=3n.
综上,当3m=2n或m=3n时,以点 P、C、D、Q 为顶点的四边形为菱形.
第3 课时 菱形的性质与判定综合
基础夯实
1. D如图,连接AC,交B D于点O,
∵四边形ABCD 是菱形,∴ BD⊥AC,OA=OC,OB=OD,∵BD=12,∴OB=OD=6.在 Rt△AOB 中,AO=
∴菱形的面积为 故选 D.
2. A ∵ 四边形ABCD 是菱形,CD=5,BD=8, . BC=CD=5,BO=DO=4,OA=OC,AC⊥BD,∴∠BOC=90°.在 Rt△OBC 中,由勾股定理得 -4 =3,∴AC=2OC=6,∵菱形ABCD 的面积=AE ,故选 A.
3.解析 (1)证明;∵四边形 ABCD 是菱形,∴AB∥CD,∴∠AFE=∠DCE,∵E是AD的中点,∴AE=DE,在△AFE与△DCE中, ∴△AFE≌△DCE(AAS),∴AF=CD.
(2)BD⊥DF.理由:如图,
·四边形ABCD 是菱形,∴AB=AD=CD,
AF=CD,∴AB=AD=AF,∴∠ABD=∠ADB,∠ADF= 90°.. BD⊥DF.
(3)当菱形ABCD满足∠ABC=60°时,四边形ACDF是菱形.
提示:∵AF=CD,AF∥CD,∴四边形ACDF 是平行四边形,∵∠ABC=60°,AB=BC,
△ABC是等边三角形,∴AB=AC,∴AC=CD,平行四边形ACDF 是菱形.
4.解析 (1)证明:··四边形 ABCD 是平行四边形,
∴AD∥BC,..∠OAF=∠OCE,
∵EF 垂直平分AC,∴EF⊥AC,OA=OC,在△AOF和△COE中.
∴△AOF≌△COE(ASA),
∴OE=OF,∴ 四边形AECF 是平行四边形,
又∵EF⊥AC,∴平行四边形AECF是菱形.
(2)由(1)知,OE=OF,四边形 AECF 是菱形,∴CE=AE=12.
∵ AC ⊥AB,EF ⊥AC,∴ ∠COE = 90°,EF ∥AB,
∴EF=2OE=12 ,.. 菱形 AECF 的面积
能力提升
5.解析 (1)证明:∵四边形ABCD 是平行四边形,OB=OD= BD,∵BD=2AB,∴AB=OB,∵AE∥BD,OE∥AB,∴四边形ABOE 是平行四边形,又∵AB=OB,∴平行四边形ABOE 是菱形.
(2)如图,连接BE,交 OA 于 F,∵四边形ABOE是菱形,∴OA⊥ B BE = 2BE, .. BE = 6 , . . BF = 3 ,.. OB = ,即 BD 的长为
6.解析 (1)证明:∵ △ABC 是等边三角形,∴AB=BC,∠ABC=60°,
E 为AB 中点,..BE= AB,.. BE=BD,
.△BED是等边三角形,∴BE=BD=DE,
由作图知,DF平分∠EDB,∴∠EDF=∠FDB,
·· EF∥BC,. ∠EFD =∠FDB, . ∠EFD =∠EDF,. EF=ED,∴ EF=BD,..四边形BDEF 是菱形.
(2)∵ △ABC是等边三角形,AD⊥BC,
∴∠C=60°,∠ADC=90°,∠CAD=∠BAD=30°,
四边形 BDEF 是菱形,∴AG⊥FD,FG=GD.
在 Rt△AGD 中,∵
7.解析 (1)在菱形ABCD中, 16=8,
由勾股定理得 12,∴菱形ABCD 的面积
(2)不发生变化.理由:如图①,连接AO,则 即
∴OE+OF=9.6,
故OE+OF 的值不发生变化.
(3)发生变化.
如图②,连接AO,则
即
.. OE-OF=9.6,
.. OE+OF的值发生变化,OE、OF 之间的数量关系为OE-OF=9.6.
微专题 对角线互相垂直的四边形的面积例题 解析 结论:两对角线乘积的一半.
应用:
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
