1.3 正方形的性质与判定同步练习(2课时,含答案) 2025-2026学年北师大版数学九年级上册
文档属性
| 名称 | 1.3 正方形的性质与判定同步练习(2课时,含答案) 2025-2026学年北师大版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 268.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 21:42:19 | ||
图片预览



文档简介
1.3 正方形的性质与判定
第1课时 正方形的性质
基础夯实
知识点 1 正方形的定义
1.一个四边形顺次添加下列条件中的三个条件便得到正方形:
a.两组对边分别相等 b.一组对边平行且相等
c.一组邻边相等 d.一个角是直角
顺次添加的条件:①a→c→d;②b→d→c;③a→b→c.则正确的是 ( )
A.仅① B.仅③ C.①② D.②③
知识点 2 正方形的性质
2.「2025广东深圳龙岗月考」菱形、正方形一定具有而矩形不一定具有的性质是 ( )
A.对边相等 B.对边平行
C.对角线互相平分 D.对角线互相垂直
3.「2025吉林长春月考」如图,在正方形 ABCD 中,点 G在BC边上,DE⊥AG于点 E,BF⊥AG 于点 F,若BF=12,DE=16,则EF的长为 ( )
A.12 B.8 C.6 D.4
4.「2023贵州贵阳期中」如图,在平面直角坐标系中,正方形OABC的顶点O,B的坐标分别是(0,0),(4,0),则顶点 C的坐标是 ( )
A.(2,2) B.(2,-2)
C.(-2,2) D.(2 ,-2)
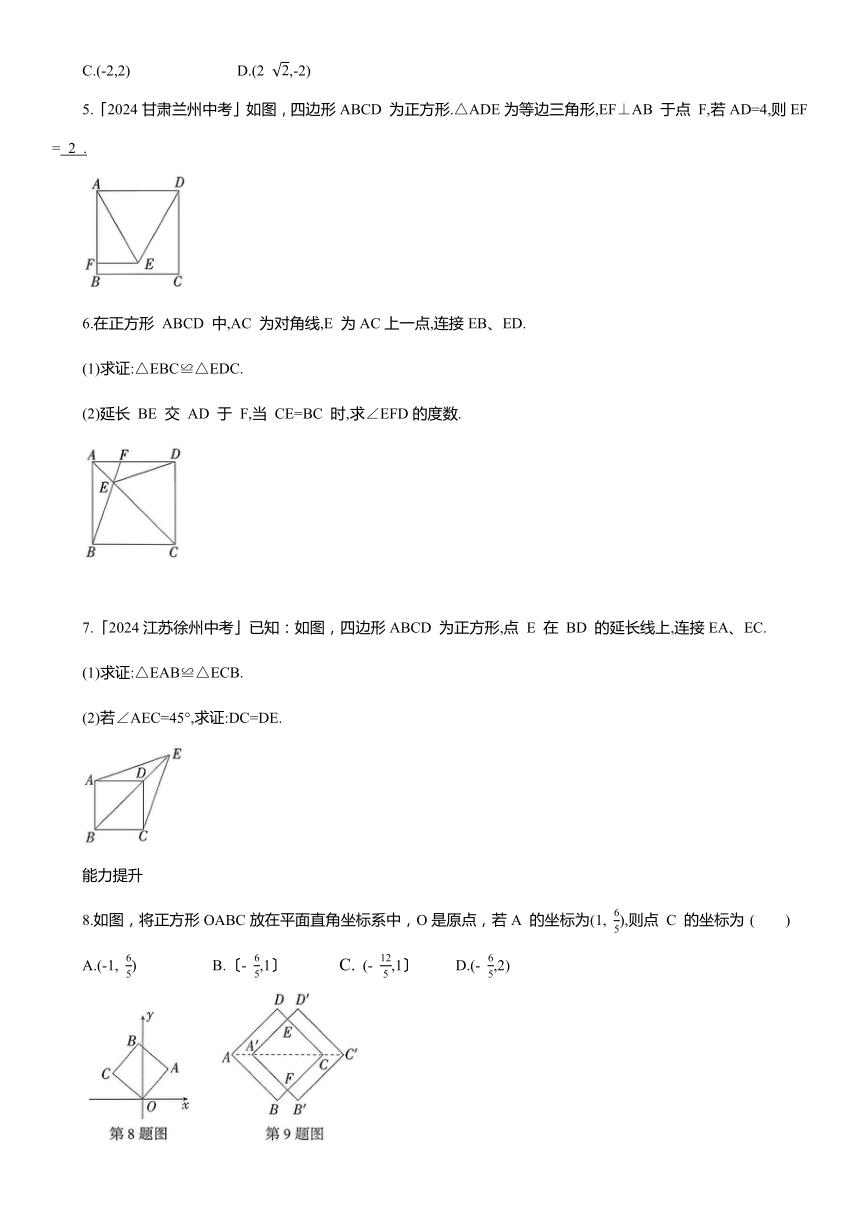
5.「2024甘肃兰州中考」如图,四边形ABCD 为正方形.△ADE为等边三角形,EF⊥AB 于点 F,若AD=4,则EF= 2 .
6.在正方形 ABCD 中,AC 为对角线,E 为AC上一点,连接EB、ED.
(1)求证:△EBC≌△EDC.
(2)延长 BE 交 AD 于 F,当 CE=BC 时,求∠EFD的度数.
7.「2024江苏徐州中考」已知:如图,四边形ABCD 为正方形,点 E 在 BD 的延长线上,连接EA、EC.
(1)求证:△EAB≌△ECB.
(2)若∠AEC=45°,求证:DC=DE.
能力提升
8.如图,将正方形OABC放在平面直角坐标系中,O是原点,若A 的坐标为(1, ),则点 C 的坐标为 ( )
A.(-1, ) B.〔- ,1〕 C. (- ,1〕 D.(- ,2)
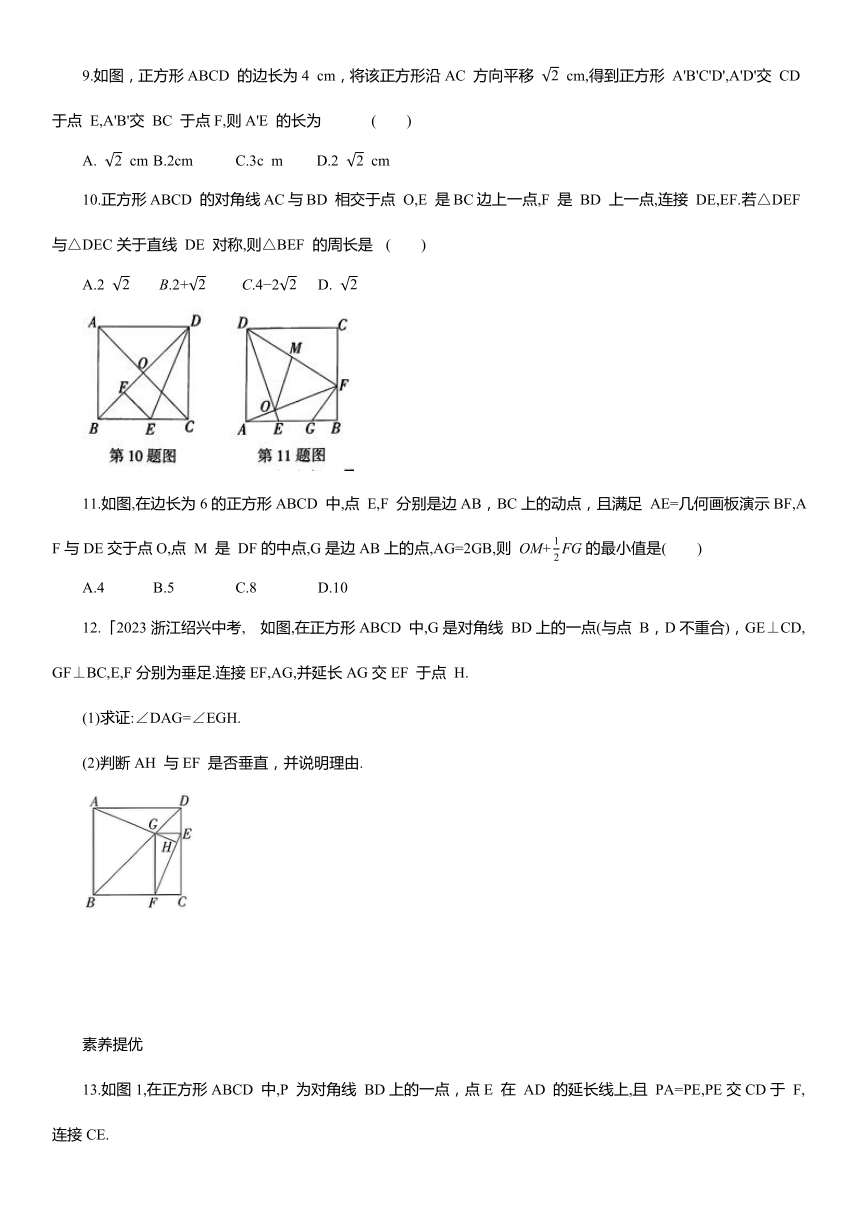
9.如图,正方形ABCD 的边长为4 cm,将该正方形沿AC 方向平移 cm,得到正方形 A'B'C'D',A'D'交 CD 于点 E,A'B'交 BC 于点F,则A'E 的长为 ( )
A. cm B.2cm C.3c m D.2 cm
10.正方形ABCD 的对角线AC与BD 相交于点 O,E 是BC边上一点,F 是 BD 上一点,连接 DE,EF.若△DEF 与△DEC关于直线 DE 对称,则△BEF 的周长是 ( )
A.2 D.
11.如图,在边长为6的正方形ABCD 中,点 E,F 分别是边AB,BC上的动点,且满足 AE=几何画板演示BF,AF与DE交于点O,点 M 是 DF的中点,G是边AB上的点,AG=2GB,则 的最小值是( )
A.4 B.5 C.8 D.10
12.「2023浙江绍兴中考, 如图,在正方形ABCD 中,G是对角线 BD上的一点(与点 B,D不重合),GE⊥CD,GF⊥BC,E,F分别为垂足.连接EF,AG,并延长AG交EF 于点 H.
(1)求证:∠DAG=∠EGH.
(2)判断AH 与EF 是否垂直,并说明理由.
素养提优
13.如图1,在正方形ABCD 中,P 为对角线 BD上的一点,点E 在 AD 的延长线上,且 PA=PE,PE交CD于 F,连接CE.
(1)求证:△PCE是等腰直角三角形.
(2)如图2,把正方形ABCD 改为菱形ABCD,其他条件不变,当∠ABC=120°时,判断△PCE的形状,并说明理由.
第2课时 正方形的判定
基础夯实
知识点 1 正方形的判定
1.如图,已知 ABCD的对角线AC,BD交于点O,添加选项中的条件后,不能证明 ABCD是正方形的为 ( )
A. AB=AD,AC=BD
B. AB=BC,AC⊥BD
C.∠BAD=90°,AC⊥BD
D.∠AOD=90°,AO=DO
2.如图,将矩形纸片ABCD 折叠,使点 A 落在 BC 上的点 F 处,折痕为 BE,若沿 EF 剪下,则折叠部分是一个正方形,其数学原理是 ( )
A.邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形
D.轴对称图形是正方形
3.已知:如图, △ABC 中, ∠ACB = 90°, CD 平分∠ACB,DE⊥AC,DF⊥BC,垂足分别为 E、F.求证:四边形 CEDF 是正方形.
知识点 2 中点四边形
4.如图,点E、F、G、H分别是四边形ABCD 边AB、BC、CD、DA 的中点.现有下列说法:①若AC⊥BD,则四边形 EFGH为矩形;②若AC=BD,则四边形 EFGH为菱形;③若四边形 EFGH 是平行四边形,则AC与 BD 互相平分;④若四边形 EFGH 是正方形,则AC 与 BD 互相垂直且相等.其中正确的个数是( )
A.1 B.2 C.3 D.4
知识点3 正方形的性质与判定的综合
5.如图,正方形ABCD的对角线AC与BD 交于点 O,分别过点 C、点 D 作 CE∥BD,DE∥AC.求证:四边形OCED 是正方形.
能力提升
6.「2025山东青岛大学附中, 」如图,点D、E、F分别是AB、BC、AC 的中点,连接DE、EF、AE、DF.
(1)求证:AE,DF互相平分.
(2)现有三个条件:①∠BAC = 90°;②AE 平分∠BAC;③AE⊥BC.
请你从中选择两个条件(写序号): ,使得四边形ADEF 是正方形,并加以证明.
7.已知:如图1,在正方形ABCD中,E,F分别是BC,CD上的点,AE、BF 相交于点 P,并且AE=BF.
(1)判断AE 和 BF 的位置关系,并说明理由.
(2)如图2,DN⊥AE,FM⊥DN,点 F 在线段 CD 上运动时(点F 不与点 C、D重合),四边形FMNP 能否成为正方形 请说明理由.
素养提优
8.新默赤意创新意识 新建新定义题 我们将菱形、矩形与正方形的接近程度称为菱形或矩形的“接近度”.
(1)设菱形相邻两个内角的度数分别为m°,n°,若我们将菱形的“接近度”定义为|m-n|,则:
①当菱形的一个内角为75°时,“接近度”= ;
②当菱形的“接近度”= 时,菱形为正方形.
(2)设菱形相邻两个内角的度数分别为m°,n°,若我们将菱形的“接近度”定义为 则:
①当菱形的一个内角为 45°时,“接近度”= ;
②当菱形的“接近度”= 时,菱形为正方形.
(3)小军同学给出了如下矩形的“接近度”的定义:设矩形相邻两边的长分别是 a和b(a≤b),将矩形的“接近度”定义为 ,于是 越小,矩形越接近正方形.
你认为他的定义 (填“合理”或“不合理”),并说明理由.
3 正方形的性质与判定
第1课时 正方形的性质
基础夯实
1. C①添加a得到四边形是平行四边形,添加c得到平行四边形是菱形,再添加d 得到菱形是正方形,故①正确;②添加b得到四边形是平行四边形,添加d 得到平行四边形是矩形,再添加 c 得到矩形是正方形,故②正确;③添加a得到四边形是平行四边形,添加b 得到平行四边形仍是平行四边形,再添加c得到平行四边形是菱形,不能得到四边形是正方形,故③不正确.故选 C.
2. D选项A,菱形、正方形、矩形的对边相等,故本选项不符合题意;选项B,菱形、正方形、矩形的对边平行,故本选项不符合题意;选项C,菱形、正方形、矩形的对角线互相平分,故本选项不符合题意;选项D,菱形、正方形的对角线互相垂直,矩形的对角线不一定互相垂直,故本选项符合题意.故选 D.
D ∵ 四边形 ABCD 是正方形,∴ AB=DA,∠BAD=90°,∵ BF⊥AG 于点 F,DE⊥AG 于点 E,∴ ∠AFB=∠DEA=90°,∴∠BAF=∠ADE=90°-∠DAE.
在△BAF 和△ADE 中, △ADE(AAS),∴BF=AE=12,AF=DE=16,∴EF=AF-AE=16-12=4,故选 D.
4. B 连接AC,如图.
∵ 四边形 OABC 是正方形,O、B在x轴上,∴点A,C关于x轴对称,AC所在直线为OB 的垂直平分线,即A,C的横坐标均为2,根据正方形对角线相等的性质可得AC=BO=4,又∵A,C关于x轴对称,.A点纵坐标为2,C点纵坐标为-2,故C点坐标为(2,-2),故选 B.
5.答案 2
解析 · △ADE 是等边三角形,∴ AE = AD = 4,∠DAE=60°,∵ 四边形 ABCD 为正方形,∴∠BAD=
6.解析 (1)证明:∵ 四边形ABCD 是正方形,.. BC=CD,∠BCE=∠DCE=45°,又∵CE=CE,∴△EBC≌△EDC.
(2)∵CE=BC,∠ACB=45°,∴∠EBC=∠BEC=67.5°,··四边形ABCD 是正方形,.. AD∥BC,.∠AFB=∠FBC=67.5°,
∵∠EFD+∠AFB=180°,∴ ∠EFD=112.5°.
7证明 (1)∵ 四边形 ABCD 为正方形,.. AB=BC,∠ABE=∠CBE=45°.
在△EAB 和△ECB 中, △ECB(SAS).
(2)∵四边形ABCD 为正方形,.. 45°.∵ △EAB ≌△ECB, ∠AEC = 45°,∴ ∠CED =∠AEC=22.5°,∵∠BDC=∠CED+∠DCE=∠AED= 45°,∴∠DCE=45°-22.5°=22.5°,∴∠CED=∠DCE,∴DC=DE.
能力提升
8. B 如图,过点A作AE⊥x轴于点 E,过点 C 作 CF⊥x轴于点 F,∴∠OEA=∠CFO=90°.
·四边形 OABC 为正方形,∴OA=OC,∠AOC=90°,
∴ ∠AOE +∠COF = 90°,∴ ∠OAE + ∠AOE = 90°,
∴∠OAE = ∠COF, 在 △AOE 与 △OCF 中,
又∵A 的坐标为
故选B.
9 C连接DD',如图,
∵正方形ABCD 平移得到正方形A'B'C'D',
∴∠CA'D'=∠ACD=45°,DD'∥AC',
D'E=4-1=3(cm),故选 C.
10. A ∵ 正 方 形 ABCD 的边长 是 2,∴ BD = 与△DEC 关于直线 DE对称,∴ DC = DF = 2,EC = EF,. . BF =2 -2,∴△BEF的周长=BF+BE+EF=BF+BE+EC=BF+ 故选 A.
11. B ∵四边形 ABCD 是正方形,∴AD=AB,∠DAB=∠ABC=90°,又∵AE=BF,∴△ADE≌△BAF(SAS),∴∠ADE=∠BAF,
∴ ∠DOF = ∠ADO + ∠DAO = ∠BAF + ∠DAO =∠DAB=90°,∵ 点 M 是 DF 的中点, 如图所示,在AB延长线上截取BH=BG,连接FH,DH,
∵FB=FB,∠FBG=∠FBH=90°,BG=BH,∴△FBG≌△FBH(SAS),∴FH=FG,
当H、D、F三点共线时,DF+HF有最小值,即此时OM+ 有最小值,最小值为DH的长的一半,
∵AG=2GB,AB=6,∴BH=BG=2,∴AH=8.
在 Rt△ADH中,由勾股定理得
的最小值为5,故选 B.
12 解析 (1)证明:∵ 四边形 ABCD 为正方形,∠ADE=90°,∵GE⊥CD,∴∠GEC=90°,. AD∥GE,∴∠DAG=∠EGH.
(2)AH⊥EF.理由如下,连接 GC交EF于点O,如图,
∵ BD为正方形ABCD的对角线,
∴∠ADG=∠CDG=45°,
又∵ DG=DG,AD=CD,
·.△ADG≌△CDG(SAS),∴∠DAG=∠DCG.
∵四边形ABCD为正方形,∴ ∠ECF=90°,又∵ GE⊥CD,GF⊥BC,∴ 四边形 FCEG 为矩形,∴OE=OC,∴∠OEC=∠OCE,∴∠DAG=∠OEC,由(1) 得 ∠DAG = ∠EGH, ∴ ∠EGH = ∠OEC,∵∠EGH+∠GEH=∠OEC+∠GEH=∠GEC = 90°,∴∠GHE=90°,∴AH⊥EF.
素养提优
13.解析 (1)证明:如图1,
∵四边形 ABCD 是正方形,∴ AD = DC,∠ADB =∠CDB=45°,∠ADC=90°.
在△PDA 和△PDC 中. △PDC,∴PA=PC,∠3=∠1,∵ PA=PE,∴∠2=∠3,PA=PE=PC,∴∠1=∠2,又∵ ∠EDF=90°,∠DFE=∠PFC,∴ ∠FPC = ∠EDF = 90°,∵ PE = PC,∴△PEC是等腰直角三角形.
(2)△PCE是等边三角形.
理由;如图2,
∵四边形ABCD 是菱形,∴AD=DC,∠ADB=∠CDB,∠ADC = ∠ABC = 120°, 在 △PDA 和 △PDC 中,∠3=∠1,∵ PA=PE,.. ∠2= ∠3,PA = PE = PC,∴∠1=∠2,又∵∠DFE=∠PFC,∴∠EPC=∠EDC,∵ ∠ADC = 120°,∴ ∠EDC = 60°,∴ ∠EPC= 60°,∵ PE=PC,∴△PEC是等边三角形.
第2课时 正方形的判定
基础夯实
1、B 选项 A,因为AB=AD,所以 ABCD 为菱形,因为AC=BD,所以菱形ABCD 为正方形,不符合题意;选项B,因为 AB=BC,所以 ABCD 为菱形,但AC⊥BD不能证明菱形ABCD 为正方形,符合题意;选项 C,因为∠BAD=90°,所以 ABCD 为矩形,又因为AC⊥BD,所以 ABCD为正方形,不符合题意;选项D,因为∠AOD=90°,所以 ABCD为菱形,又因为AO=DO,所以菱形ABCD 为正方形,不符合题意.故选 B.
2. A 根据折叠的特性,可得∠BAD=∠BFE=90°,AB=BF,AE = EF.∵ 四边形 ABCD 是矩形,.. ∠BAD =∠ABF=90°.∵ ∠BAD=∠ABF=∠BFE=90°,.. 四边形ABFE 是矩形.∵AB=BF,∴四边形ABFE 是正方形.故选A.
3.证明 ∵CD平分∠ACB,DE⊥AC,DF⊥BC,
∴DE=DF,∠CED=∠CFD=90°,
··∠ACB=90°,∴ 四边形 CEDF 是矩形,
又∵ DE=DF,∴ 四边形 CEDF 是正方形.
4. C ∵ 点 E、F、G、H分别是四边形ABCD 边AB、BC、CD、DA 的中点,∴EF∥AC,EF= AC,GH∥AC,GH=i/ AC,EH∥BD,EH= BD,.. EF∥GH,EF=GH,∴四边形EFGH为平行四边形.①当AC⊥BD 时,EF⊥EH,则四边形 EFGH为矩形,说法正确;②当AC=BD 时,EF=EH,则四边形EFGH为菱形,说法正确;③四边形EFGH一定是平行四边形,AC 与BD 不一定互相平分,原说法错误;④当四边形EFGH是正方形时,EF⊥EH,EF=EH,则AC⊥BD,AC=BD,即AC 与 BD 互相垂直且相等,说法正确.正确的说法有3个,故选 C.
5.证明 : CE∥BD,DE∥AC,
∴ 四边形 OCED 是平行四边形,
∵四边形ABCD 是正方形,
∴OA=OC=OB=OD,AC⊥BD,
∴四边形 OCED 是正方形.
能力提升
6.解析 (1)证明:∵D、E、F分别是AB,BC,AC的中点,∴ DE、EF都是△ABC的中位线,∴ DE∥AC,EF∥AB,
∴ 四边形 ADEF为平行四边形,∴AE与DF 互相平分.
(2)答案不唯一.可选择①③,证明如下:
∵四边形ADEF 为平行四边形,∠BAC=90°,..四边形ADEF 是矩形,. 点 D、F 分别是AB、AC的中点,∴ DF是△ABC的中位线,.. DF∥BC,∵ AE⊥BC,∴AE⊥DF,∴四边形 ADEF 是正方形.
解析 (1)AE⊥BF.理由:∵四边形ABCD 是正方形,∴AB=BC,∠ABC=∠C=90°.
在 Rt△ABE和 Rt△BCF 中,AE=BF,AB=BC,. Rt△ABE≌Rt△BCF(HL),∴∠BAE=∠CBF,∴ ∠BAE +∠BEA = 90°, .. ∠CBF +∠BEA = 90°,.∠BPE=90°,∴AE⊥BF.
(2)四边形 FMNP 不能成为正方形.理由如下:
··FM⊥DN,DN⊥AE,且由(1)知AE⊥BF,四边形 FMNP 是矩形.
∠BAP+∠NAD=∠NAD+∠ADN=90°,∠BAP=∠ADN,
在△BAP 和△ADN中,
..△BAP≌△ADN(AAS),
.. BP=AN,AP=DN.
:AE=BF,∴AE-AN=BF-BP,
EN=PF,
∵点 F 在线段CD 上运动(点 F 不与点 C、D 重合),
∴ P、E不重合,∴PN≠PF,
∴ 四边形 FMNP 不能成为正方形.
素养提优
8.解析 (1)①∵菱形的一个内角为75°,..与它相邻的内角的度数为 105°.∴该菱形的“接近度”=1m-n|=|105-75|=30.故答案为30.
②当菱形的一个内角为90°时,菱形是正方形,此时菱形相邻的两内角度数为90°,90°,即当菱形的“接近度”等于190-901=0时,菱形是正方形.故答案为0.
(2)①菱形的一个内角为45°,∴与它相邻的内角的度数为135°,∴该菱形的“接近度 故答案为
②当菱形的一个内角为90°时,菱形是正方形,即当菱形的“接近度 时,菱形是正方形.故答案为 1.
不合理.理由;当 时,a=b,矩形变为正方形,
∴a/b越接近1,矩形越接近正方形,即只有矩形的“接近度"a/b越接近1,矩形才越接近正方形.
第1课时 正方形的性质
基础夯实
知识点 1 正方形的定义
1.一个四边形顺次添加下列条件中的三个条件便得到正方形:
a.两组对边分别相等 b.一组对边平行且相等
c.一组邻边相等 d.一个角是直角
顺次添加的条件:①a→c→d;②b→d→c;③a→b→c.则正确的是 ( )
A.仅① B.仅③ C.①② D.②③
知识点 2 正方形的性质
2.「2025广东深圳龙岗月考」菱形、正方形一定具有而矩形不一定具有的性质是 ( )
A.对边相等 B.对边平行
C.对角线互相平分 D.对角线互相垂直
3.「2025吉林长春月考」如图,在正方形 ABCD 中,点 G在BC边上,DE⊥AG于点 E,BF⊥AG 于点 F,若BF=12,DE=16,则EF的长为 ( )
A.12 B.8 C.6 D.4
4.「2023贵州贵阳期中」如图,在平面直角坐标系中,正方形OABC的顶点O,B的坐标分别是(0,0),(4,0),则顶点 C的坐标是 ( )
A.(2,2) B.(2,-2)
C.(-2,2) D.(2 ,-2)
5.「2024甘肃兰州中考」如图,四边形ABCD 为正方形.△ADE为等边三角形,EF⊥AB 于点 F,若AD=4,则EF= 2 .
6.在正方形 ABCD 中,AC 为对角线,E 为AC上一点,连接EB、ED.
(1)求证:△EBC≌△EDC.
(2)延长 BE 交 AD 于 F,当 CE=BC 时,求∠EFD的度数.
7.「2024江苏徐州中考」已知:如图,四边形ABCD 为正方形,点 E 在 BD 的延长线上,连接EA、EC.
(1)求证:△EAB≌△ECB.
(2)若∠AEC=45°,求证:DC=DE.
能力提升
8.如图,将正方形OABC放在平面直角坐标系中,O是原点,若A 的坐标为(1, ),则点 C 的坐标为 ( )
A.(-1, ) B.〔- ,1〕 C. (- ,1〕 D.(- ,2)
9.如图,正方形ABCD 的边长为4 cm,将该正方形沿AC 方向平移 cm,得到正方形 A'B'C'D',A'D'交 CD 于点 E,A'B'交 BC 于点F,则A'E 的长为 ( )
A. cm B.2cm C.3c m D.2 cm
10.正方形ABCD 的对角线AC与BD 相交于点 O,E 是BC边上一点,F 是 BD 上一点,连接 DE,EF.若△DEF 与△DEC关于直线 DE 对称,则△BEF 的周长是 ( )
A.2 D.
11.如图,在边长为6的正方形ABCD 中,点 E,F 分别是边AB,BC上的动点,且满足 AE=几何画板演示BF,AF与DE交于点O,点 M 是 DF的中点,G是边AB上的点,AG=2GB,则 的最小值是( )
A.4 B.5 C.8 D.10
12.「2023浙江绍兴中考, 如图,在正方形ABCD 中,G是对角线 BD上的一点(与点 B,D不重合),GE⊥CD,GF⊥BC,E,F分别为垂足.连接EF,AG,并延长AG交EF 于点 H.
(1)求证:∠DAG=∠EGH.
(2)判断AH 与EF 是否垂直,并说明理由.
素养提优
13.如图1,在正方形ABCD 中,P 为对角线 BD上的一点,点E 在 AD 的延长线上,且 PA=PE,PE交CD于 F,连接CE.
(1)求证:△PCE是等腰直角三角形.
(2)如图2,把正方形ABCD 改为菱形ABCD,其他条件不变,当∠ABC=120°时,判断△PCE的形状,并说明理由.
第2课时 正方形的判定
基础夯实
知识点 1 正方形的判定
1.如图,已知 ABCD的对角线AC,BD交于点O,添加选项中的条件后,不能证明 ABCD是正方形的为 ( )
A. AB=AD,AC=BD
B. AB=BC,AC⊥BD
C.∠BAD=90°,AC⊥BD
D.∠AOD=90°,AO=DO
2.如图,将矩形纸片ABCD 折叠,使点 A 落在 BC 上的点 F 处,折痕为 BE,若沿 EF 剪下,则折叠部分是一个正方形,其数学原理是 ( )
A.邻边相等的矩形是正方形
B.对角线相等的菱形是正方形
C.两个全等的直角三角形构成正方形
D.轴对称图形是正方形
3.已知:如图, △ABC 中, ∠ACB = 90°, CD 平分∠ACB,DE⊥AC,DF⊥BC,垂足分别为 E、F.求证:四边形 CEDF 是正方形.
知识点 2 中点四边形
4.如图,点E、F、G、H分别是四边形ABCD 边AB、BC、CD、DA 的中点.现有下列说法:①若AC⊥BD,则四边形 EFGH为矩形;②若AC=BD,则四边形 EFGH为菱形;③若四边形 EFGH 是平行四边形,则AC与 BD 互相平分;④若四边形 EFGH 是正方形,则AC 与 BD 互相垂直且相等.其中正确的个数是( )
A.1 B.2 C.3 D.4
知识点3 正方形的性质与判定的综合
5.如图,正方形ABCD的对角线AC与BD 交于点 O,分别过点 C、点 D 作 CE∥BD,DE∥AC.求证:四边形OCED 是正方形.
能力提升
6.「2025山东青岛大学附中, 」如图,点D、E、F分别是AB、BC、AC 的中点,连接DE、EF、AE、DF.
(1)求证:AE,DF互相平分.
(2)现有三个条件:①∠BAC = 90°;②AE 平分∠BAC;③AE⊥BC.
请你从中选择两个条件(写序号): ,使得四边形ADEF 是正方形,并加以证明.
7.已知:如图1,在正方形ABCD中,E,F分别是BC,CD上的点,AE、BF 相交于点 P,并且AE=BF.
(1)判断AE 和 BF 的位置关系,并说明理由.
(2)如图2,DN⊥AE,FM⊥DN,点 F 在线段 CD 上运动时(点F 不与点 C、D重合),四边形FMNP 能否成为正方形 请说明理由.
素养提优
8.新默赤意创新意识 新建新定义题 我们将菱形、矩形与正方形的接近程度称为菱形或矩形的“接近度”.
(1)设菱形相邻两个内角的度数分别为m°,n°,若我们将菱形的“接近度”定义为|m-n|,则:
①当菱形的一个内角为75°时,“接近度”= ;
②当菱形的“接近度”= 时,菱形为正方形.
(2)设菱形相邻两个内角的度数分别为m°,n°,若我们将菱形的“接近度”定义为 则:
①当菱形的一个内角为 45°时,“接近度”= ;
②当菱形的“接近度”= 时,菱形为正方形.
(3)小军同学给出了如下矩形的“接近度”的定义:设矩形相邻两边的长分别是 a和b(a≤b),将矩形的“接近度”定义为 ,于是 越小,矩形越接近正方形.
你认为他的定义 (填“合理”或“不合理”),并说明理由.
3 正方形的性质与判定
第1课时 正方形的性质
基础夯实
1. C①添加a得到四边形是平行四边形,添加c得到平行四边形是菱形,再添加d 得到菱形是正方形,故①正确;②添加b得到四边形是平行四边形,添加d 得到平行四边形是矩形,再添加 c 得到矩形是正方形,故②正确;③添加a得到四边形是平行四边形,添加b 得到平行四边形仍是平行四边形,再添加c得到平行四边形是菱形,不能得到四边形是正方形,故③不正确.故选 C.
2. D选项A,菱形、正方形、矩形的对边相等,故本选项不符合题意;选项B,菱形、正方形、矩形的对边平行,故本选项不符合题意;选项C,菱形、正方形、矩形的对角线互相平分,故本选项不符合题意;选项D,菱形、正方形的对角线互相垂直,矩形的对角线不一定互相垂直,故本选项符合题意.故选 D.
D ∵ 四边形 ABCD 是正方形,∴ AB=DA,∠BAD=90°,∵ BF⊥AG 于点 F,DE⊥AG 于点 E,∴ ∠AFB=∠DEA=90°,∴∠BAF=∠ADE=90°-∠DAE.
在△BAF 和△ADE 中, △ADE(AAS),∴BF=AE=12,AF=DE=16,∴EF=AF-AE=16-12=4,故选 D.
4. B 连接AC,如图.
∵ 四边形 OABC 是正方形,O、B在x轴上,∴点A,C关于x轴对称,AC所在直线为OB 的垂直平分线,即A,C的横坐标均为2,根据正方形对角线相等的性质可得AC=BO=4,又∵A,C关于x轴对称,.A点纵坐标为2,C点纵坐标为-2,故C点坐标为(2,-2),故选 B.
5.答案 2
解析 · △ADE 是等边三角形,∴ AE = AD = 4,∠DAE=60°,∵ 四边形 ABCD 为正方形,∴∠BAD=
6.解析 (1)证明:∵ 四边形ABCD 是正方形,.. BC=CD,∠BCE=∠DCE=45°,又∵CE=CE,∴△EBC≌△EDC.
(2)∵CE=BC,∠ACB=45°,∴∠EBC=∠BEC=67.5°,··四边形ABCD 是正方形,.. AD∥BC,.∠AFB=∠FBC=67.5°,
∵∠EFD+∠AFB=180°,∴ ∠EFD=112.5°.
7证明 (1)∵ 四边形 ABCD 为正方形,.. AB=BC,∠ABE=∠CBE=45°.
在△EAB 和△ECB 中, △ECB(SAS).
(2)∵四边形ABCD 为正方形,.. 45°.∵ △EAB ≌△ECB, ∠AEC = 45°,∴ ∠CED =∠AEC=22.5°,∵∠BDC=∠CED+∠DCE=∠AED= 45°,∴∠DCE=45°-22.5°=22.5°,∴∠CED=∠DCE,∴DC=DE.
能力提升
8. B 如图,过点A作AE⊥x轴于点 E,过点 C 作 CF⊥x轴于点 F,∴∠OEA=∠CFO=90°.
·四边形 OABC 为正方形,∴OA=OC,∠AOC=90°,
∴ ∠AOE +∠COF = 90°,∴ ∠OAE + ∠AOE = 90°,
∴∠OAE = ∠COF, 在 △AOE 与 △OCF 中,
又∵A 的坐标为
故选B.
9 C连接DD',如图,
∵正方形ABCD 平移得到正方形A'B'C'D',
∴∠CA'D'=∠ACD=45°,DD'∥AC',
D'E=4-1=3(cm),故选 C.
10. A ∵ 正 方 形 ABCD 的边长 是 2,∴ BD = 与△DEC 关于直线 DE对称,∴ DC = DF = 2,EC = EF,. . BF =2 -2,∴△BEF的周长=BF+BE+EF=BF+BE+EC=BF+ 故选 A.
11. B ∵四边形 ABCD 是正方形,∴AD=AB,∠DAB=∠ABC=90°,又∵AE=BF,∴△ADE≌△BAF(SAS),∴∠ADE=∠BAF,
∴ ∠DOF = ∠ADO + ∠DAO = ∠BAF + ∠DAO =∠DAB=90°,∵ 点 M 是 DF 的中点, 如图所示,在AB延长线上截取BH=BG,连接FH,DH,
∵FB=FB,∠FBG=∠FBH=90°,BG=BH,∴△FBG≌△FBH(SAS),∴FH=FG,
当H、D、F三点共线时,DF+HF有最小值,即此时OM+ 有最小值,最小值为DH的长的一半,
∵AG=2GB,AB=6,∴BH=BG=2,∴AH=8.
在 Rt△ADH中,由勾股定理得
的最小值为5,故选 B.
12 解析 (1)证明:∵ 四边形 ABCD 为正方形,∠ADE=90°,∵GE⊥CD,∴∠GEC=90°,. AD∥GE,∴∠DAG=∠EGH.
(2)AH⊥EF.理由如下,连接 GC交EF于点O,如图,
∵ BD为正方形ABCD的对角线,
∴∠ADG=∠CDG=45°,
又∵ DG=DG,AD=CD,
·.△ADG≌△CDG(SAS),∴∠DAG=∠DCG.
∵四边形ABCD为正方形,∴ ∠ECF=90°,又∵ GE⊥CD,GF⊥BC,∴ 四边形 FCEG 为矩形,∴OE=OC,∴∠OEC=∠OCE,∴∠DAG=∠OEC,由(1) 得 ∠DAG = ∠EGH, ∴ ∠EGH = ∠OEC,∵∠EGH+∠GEH=∠OEC+∠GEH=∠GEC = 90°,∴∠GHE=90°,∴AH⊥EF.
素养提优
13.解析 (1)证明:如图1,
∵四边形 ABCD 是正方形,∴ AD = DC,∠ADB =∠CDB=45°,∠ADC=90°.
在△PDA 和△PDC 中. △PDC,∴PA=PC,∠3=∠1,∵ PA=PE,∴∠2=∠3,PA=PE=PC,∴∠1=∠2,又∵ ∠EDF=90°,∠DFE=∠PFC,∴ ∠FPC = ∠EDF = 90°,∵ PE = PC,∴△PEC是等腰直角三角形.
(2)△PCE是等边三角形.
理由;如图2,
∵四边形ABCD 是菱形,∴AD=DC,∠ADB=∠CDB,∠ADC = ∠ABC = 120°, 在 △PDA 和 △PDC 中,∠3=∠1,∵ PA=PE,.. ∠2= ∠3,PA = PE = PC,∴∠1=∠2,又∵∠DFE=∠PFC,∴∠EPC=∠EDC,∵ ∠ADC = 120°,∴ ∠EDC = 60°,∴ ∠EPC= 60°,∵ PE=PC,∴△PEC是等边三角形.
第2课时 正方形的判定
基础夯实
1、B 选项 A,因为AB=AD,所以 ABCD 为菱形,因为AC=BD,所以菱形ABCD 为正方形,不符合题意;选项B,因为 AB=BC,所以 ABCD 为菱形,但AC⊥BD不能证明菱形ABCD 为正方形,符合题意;选项 C,因为∠BAD=90°,所以 ABCD 为矩形,又因为AC⊥BD,所以 ABCD为正方形,不符合题意;选项D,因为∠AOD=90°,所以 ABCD为菱形,又因为AO=DO,所以菱形ABCD 为正方形,不符合题意.故选 B.
2. A 根据折叠的特性,可得∠BAD=∠BFE=90°,AB=BF,AE = EF.∵ 四边形 ABCD 是矩形,.. ∠BAD =∠ABF=90°.∵ ∠BAD=∠ABF=∠BFE=90°,.. 四边形ABFE 是矩形.∵AB=BF,∴四边形ABFE 是正方形.故选A.
3.证明 ∵CD平分∠ACB,DE⊥AC,DF⊥BC,
∴DE=DF,∠CED=∠CFD=90°,
··∠ACB=90°,∴ 四边形 CEDF 是矩形,
又∵ DE=DF,∴ 四边形 CEDF 是正方形.
4. C ∵ 点 E、F、G、H分别是四边形ABCD 边AB、BC、CD、DA 的中点,∴EF∥AC,EF= AC,GH∥AC,GH=i/ AC,EH∥BD,EH= BD,.. EF∥GH,EF=GH,∴四边形EFGH为平行四边形.①当AC⊥BD 时,EF⊥EH,则四边形 EFGH为矩形,说法正确;②当AC=BD 时,EF=EH,则四边形EFGH为菱形,说法正确;③四边形EFGH一定是平行四边形,AC 与BD 不一定互相平分,原说法错误;④当四边形EFGH是正方形时,EF⊥EH,EF=EH,则AC⊥BD,AC=BD,即AC 与 BD 互相垂直且相等,说法正确.正确的说法有3个,故选 C.
5.证明 : CE∥BD,DE∥AC,
∴ 四边形 OCED 是平行四边形,
∵四边形ABCD 是正方形,
∴OA=OC=OB=OD,AC⊥BD,
∴四边形 OCED 是正方形.
能力提升
6.解析 (1)证明:∵D、E、F分别是AB,BC,AC的中点,∴ DE、EF都是△ABC的中位线,∴ DE∥AC,EF∥AB,
∴ 四边形 ADEF为平行四边形,∴AE与DF 互相平分.
(2)答案不唯一.可选择①③,证明如下:
∵四边形ADEF 为平行四边形,∠BAC=90°,..四边形ADEF 是矩形,. 点 D、F 分别是AB、AC的中点,∴ DF是△ABC的中位线,.. DF∥BC,∵ AE⊥BC,∴AE⊥DF,∴四边形 ADEF 是正方形.
解析 (1)AE⊥BF.理由:∵四边形ABCD 是正方形,∴AB=BC,∠ABC=∠C=90°.
在 Rt△ABE和 Rt△BCF 中,AE=BF,AB=BC,. Rt△ABE≌Rt△BCF(HL),∴∠BAE=∠CBF,∴ ∠BAE +∠BEA = 90°, .. ∠CBF +∠BEA = 90°,.∠BPE=90°,∴AE⊥BF.
(2)四边形 FMNP 不能成为正方形.理由如下:
··FM⊥DN,DN⊥AE,且由(1)知AE⊥BF,四边形 FMNP 是矩形.
∠BAP+∠NAD=∠NAD+∠ADN=90°,∠BAP=∠ADN,
在△BAP 和△ADN中,
..△BAP≌△ADN(AAS),
.. BP=AN,AP=DN.
:AE=BF,∴AE-AN=BF-BP,
EN=PF,
∵点 F 在线段CD 上运动(点 F 不与点 C、D 重合),
∴ P、E不重合,∴PN≠PF,
∴ 四边形 FMNP 不能成为正方形.
素养提优
8.解析 (1)①∵菱形的一个内角为75°,..与它相邻的内角的度数为 105°.∴该菱形的“接近度”=1m-n|=|105-75|=30.故答案为30.
②当菱形的一个内角为90°时,菱形是正方形,此时菱形相邻的两内角度数为90°,90°,即当菱形的“接近度”等于190-901=0时,菱形是正方形.故答案为0.
(2)①菱形的一个内角为45°,∴与它相邻的内角的度数为135°,∴该菱形的“接近度 故答案为
②当菱形的一个内角为90°时,菱形是正方形,即当菱形的“接近度 时,菱形是正方形.故答案为 1.
不合理.理由;当 时,a=b,矩形变为正方形,
∴a/b越接近1,矩形越接近正方形,即只有矩形的“接近度"a/b越接近1,矩形才越接近正方形.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
