人教版必修一 1.3 位置变化快慢的描述——速度(共31张PPT)
文档属性
| 名称 | 人教版必修一 1.3 位置变化快慢的描述——速度(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 32.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-08-22 17:35:23 | ||
图片预览











文档简介
(共31张PPT)
第 3 节 位置变化快慢的描述——速度
第一章 运动的描述
1.理解速度的物理意义,知道速度是矢量.
2.理解平均速度和瞬时速度的区别,知道速率的概念.
3.会用平均速度公式进行相关的计算.
教学目标
生活和科学研究中经常需要知道物体运动的快慢和方向。不同的运动,快慢程度并不相同。同学们猜想下是汽车快还是飞机快?
情景引入
A
B
O
1
5
cm
Δt=4s
xA=1cm
xB=5cm
O
100
500
m
Δt=10s
xC=100m
C
D
Δx= xB- xA=4cm
xD=500m
Δx = xD- xC=400m
速度
如何比较物体运动的快慢呢?
可以用单位时间内的位移来表示运动的快慢
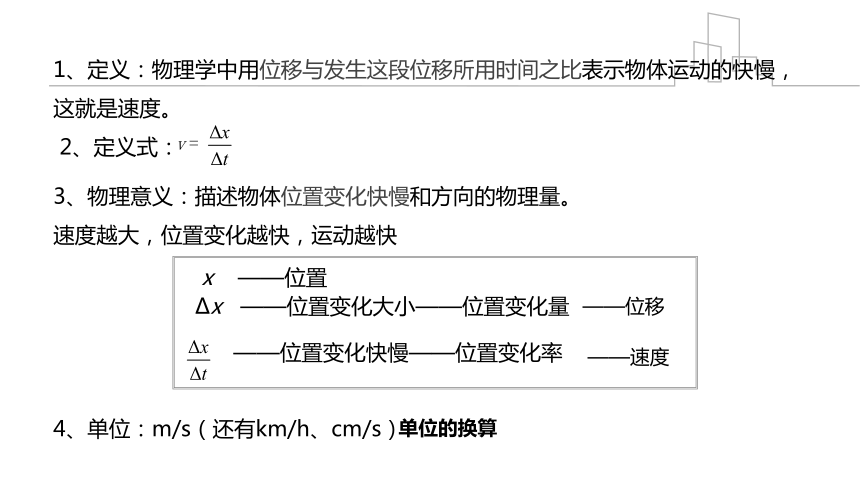
1、定义:物理学中用位移与发生这段位移所用时间之比表示物体运动的快慢,这就是速度。
2、定义式:
3、物理意义:描述物体位置变化快慢和方向的物理量。
速度越大,位置变化越快,运动越快
4、单位:m/s(还有km/h、cm/s)
单位的换算
x ——位置
Δx ——位置变化大小——位置变化量
——位置变化快慢——位置变化率
——位移
——速度
5、速度是矢量:
大小:数值上等于单位时间内位移的大小。
方向:物体运动的方向。
6、比值定义法:用两个物理量的比值来定义一个新的物理量,这个新物理量与前两个物理量不直接成比例关系。
思考:两辆汽车从某地出发,速度都是20m/s,他们的运动情况完全相同吗?
可能是背道而驰 !!
v与Δx、Δt不直接成比例关系
注意:这里的速度和初中所学速度的含义不完全相同。
1、关于几个物理量的的说法正确的是( )
A.速度越大,物体的位移越大
B.速度越大,物体的位置变化越大
C.速度越大,物体的位置变化越快
D.速度越大,物体在单位时间内的位移越大
CD
课堂训练
2、关于速度的说法,下列各项中正确的是( )
A.速度是描述物体运动快慢的物理量,速度大表示物体运动的快
B.速度描述物体的位置变化快慢,速度大的表示物体位置变化大
C.速度越大,位置变化越快,位移也就越大
D.v1=2m/s,v2=-3m/s,v1表示的速度大
A
1、平均速度:
定义:物体在时间Δt内运动的平均快慢程度。运动物体的位移Δx与发生这段位移所用时间Δt的比值。
公式:
物理意义:粗略描述物体在时间Δt内运动的快慢和方向。
平均速度是矢量,既有大小又有方向。
方向:与Δx的方向相同,由初位置指向末位置。
平均速度和瞬时速度
求平均速度必须指明是求哪段时间(或哪段位移)的平均速度。
Δx与Δt的同一性和对应性
例1、做单向直线运动的一辆自行车在第一个5s内的位移为10m,第二个5s内的位移为15m,第三个5s内的位移为12m,第四个5s内的位移为15m。请分别求出它在每个5s内的平均速度以及这20s内的平均速度 第二个5s内的运动情况和第4个5s内的运动情况一定完全一样吗?
v1=2m/s;v2=3m/s;v3=2.4m/s;v4=3m/s;v=2.6m/s
例2、物体沿一条直线由A运动到B,
(1)若前1/3时间做速度为v1的匀速运动,后2/3时间做速度为v2的匀速运动,求物体从A到B的平均速度。
(2)若前1/3位移做速度为v1的匀速运动,后2/3位移做速度为v2的匀速运动,求物体从A到B的平均速度。
平均速度不是速度的平均值
t
(t+Δt )
可用时刻 t 到 t +Δt 一小段时间内的平均速度 来代替时刻 t 物体的速度,Δt 越小,运动快慢的差异就越小。当 Δt 非常非常小时,运动快慢的差异可以忽略不计,就可认为是t时刻的速度。
Δx
思考讨论:平均速度描述物体在一段时间内运动的平均快慢程度及方向。那么,怎样描述物体在某一时刻运动的快慢和方向呢?
2、瞬时速度
(1)定义:物体经过某一位置或在某一时刻的运动快慢程度就是瞬时速度。
(2)物理意义:瞬时速度精确地描述了物体运动的快慢。
(3)瞬时速度是矢量,既有大小又有方向。
方向:与物体在某一时刻或某一位置的运动方向相同。
大小:叫做瞬时速率、即时速率,简称速率。
(4)匀速直线运动是瞬时速度保持不变的运动。
在匀速直线运动中,平均速度与瞬时速度相等。
汽车速度计不能显示车辆运动的方向,它的示数实际是汽车的速率。
注意:日常生活中说到的“速度”,有时是指速率,要根据上下文判断。
例3、利用如图所示装置可以测量滑块从木板上下滑时通过光电门的速度。图中MN是水平桌面,PQ是木板,1和2是固定在木板上适当位置的两个光电门(与之连接的两个光电计时器没有画出)。让滑块从木板的顶端滑下,光电门1、2各自连接的计时器显示的挡光时间分别为5.0×10-2s和2.0×10-2s。小滑块的宽度d为0.5cm,则滑块通过光电门1的速度v1= ______m/s,滑块通过光电门2的速度v2= ______m/s。(结果保留两位有效数字)
0.10
0.25
3、下面的几个速度中表示瞬时速度的是 。
A.百米赛跑的运动员以9.5 m/s的速度冲过终点线
B.汽车从甲站行驶到乙站的速度是40 km/h
C.某同学从家里到学校步行速度为1.5 m/s
D.经提速后某动车的运行速度最高可达486 km/h
E.由于堵车,在隧道内的车速仅为1.2 m/s
F.返回地面的太空舱以8 m/s的速度落入太平洋中
G.汽车以72 km/h的速度通过长江大桥全程
H.子弹射出枪口的速度是800 m/s
I.小球第3 s末的速度是6 m/s
ADFHI
课堂训练
测量平均速度 用手拉通过打点计时器的纸带时,纸带运动确定时间内的位移就被记录下来,据此可以计算纸带运动的速度。
如图是打点计时器打出的一条纸带示意图。若想计算实验时运动纸带在D、G两点的
平均速度,只需测出D、G间的位移Δx和所用时间Δt,就可以算出平均速度:
计算每隔0.1s的平均速度纸带示意图
实验:测量纸带的平均速度和瞬时速度
每隔0.1s(或更短)计算一次平均速度。
1. 在图中选取纸带上一点为起始点0,后面每5个点取一个计数点,分别用数字1,2,3,...标出这些计数点;
2. 测量各计数点到起始点0的距离x,记录在表1中;
3. 计算两相邻计数点间的位移Δx 同时记录对应的时间Δt ;
4. 根据Δx和Δt计算纸带在相邻计数点间的平均速度v 。
位置 0 1 2 3 4 ...
x/m
Δx /m
Δt /s
v/(m/s)
表1 手拉纸带的位移和平均速度
测量瞬时速度 下面考虑如何测量图中E点的瞬时速度。
E点在D、G两点之间,D、G两点间的平均速度也可以求出。如果不要求很精确,用这个平均速度粗略地代表E点的瞬时速度,也未尝不可,如果把包含E点在内的间隔取得小一些,例如取图中的DF线段,那么经过D、F两点所用的时间Δt就会变短,用两点间位移Δx和时间Δt算出的平均速度代表纸带在E点瞬时速度,就会精确一些。D、F两点离E点越近,算出的平均速度越接近E点的瞬时速度。
D、F两点间的距离过小,测量误差会增大。所以实际测量过程中要根据需要及所用仪器的情况,在要测量的点附近选取合适的位移和时间。请考虑此实验中产生误差的原因。
思考:此实验中产生误差的原因有哪些?
请根据上述测量瞬时速度的方法,计算上节实验中纸带上各级计数点的瞬时速度。 每隔0.06s计算一次速度。
1. 从纸带起始点0算起,后面每3个点取一个计数点;
2. 测量各计数点到起始点0的距离x,记录在表2中;
3. 计算两相邻计数点间的位移 Δx,同时记录对应的时间Δt;
4. 根据Δx和Δt算出的速度值就可以代表在Δx这一区间内任意一点的瞬时速度。
将算出的各计数点的速度值记录在下表中。
计算每隔0.06s的平均速度纸带示意图
位置 0 1 2 3 4 ...
x/m
Δx /m
Δt /s
v/(m/s)
表2 手拉纸带各计数点的瞬时速度
(1)建立坐标系:以时间t为横轴,速度v为纵轴;
(2)描点;
(3)用平滑的曲线连起来。
v/(m·s-1)
t/s
O
作图步骤:
速度—时间图像或v-t图像
物体运动的速度随时间变化的情况可以用图来直观表示。以时间t横轴,速度v为纵轴,坐标中的图像为速度—时间图像或v-t图像。
速度-时间(v-t)图象
t/s 0 1 2 3 4 5 6 7
v m/s 0.05 0.10 0.20 0.30 0.28 0.28 0.46 0.55
0 1 2 3 4 5 6 7
0.6
0.5
0.4
0.3
0.2
0.1
t/10-1s
v/(m·s-1)
用图像表示速度
4、如下图是一个物体运动的v-t图象,从以下三个方面说明它的速度是怎样变化的.
(1)物体是从静止开始运动还是具有一定的初速度?
(2)运动的方向是否变化?
(3)速度的大小是否变化?怎样变化?
答案:(1)具有一定的初速度;
(2)运动方向在t3时刻发生变化;
(3)0~t1时间段内,速度均匀增大;t1~t2时间段内,速度不变;
t2~t3时间段内,速度均匀减小;t3时刻后,速度反向均匀增加。
课堂训练
1、物理学中用位移与发生这段位移所用时间之比表示物体速度。
2、速度是矢量,它既有大小,又有方向。 v的方向是由对应Δt时间内位移Δx的方向决定。
3、平均速度:粗略地描述了物体运动快慢程度和方向。
4、瞬时速度精确地描述了物体运动的快慢和方向。
5、测量纸带的平均速度和瞬时速度。
6、速度—时间图像。
课堂总结
1、 (多选)如图所示,一人骑自行车晨练,由静止开始沿直线运动,她在第1 s内、第2 s内、第3 s内、第4 s内通过的位移分别为1 m、2 m、3 m、4 m,则( )
A.她在4 s末的瞬时速度为4 m/s
B.她在第2 s内的平均速度为2 m/s
C.她在4 s内的平均速度为2.5 m/s
D.她在1 s末的速度为1 m/s
BC
解析:由 可得该人在第2s内的平均速度为2m/s,B正确;前4s内的平均速速
为 m/s=2.5m/s,C正确;因无法确定该人的瞬时速度,A、D错误。
跟踪练习
2、在110 m跨栏比赛中,某运动员用了13.15秒跑完全程。通过测量,测得他在5秒末的速度是8.00 m/s,到达终点的速度是9.80 m/s,则以下有关平均速度和瞬时速度的说法中正确的是( )
A.8.00 m/s是瞬时速度
B.9.80 m/s是全程的平均速度
C.全程的平均速度是8.90 m/s
D.全程的平均速度是8.37 m/s
AD
3、物体沿直线运动,下列说法中正确的是( )
A.物体在某时刻的速度为3 m/s,则该物体在1 s内的位移一定是3 m
B.物体在某1 s内的平均速度为3 m/s,则物体在这1 s内的位移一定是3 m
C.物体在某段时间内的平均速度为3 m/s,则物体在第1 s内的位移一定是3 m
D.物体在某段时间内的平均速度为3 m/s,则物体在任意1 s内的位移一定是3 m
B
Δx与Δt的同一性和对应性
解析:AC=14.0 mm,AC间的平均速度为 =2×0.02(14.0×10-3) m/s=0.35 m/s;AD=25.0 mm,AD间的平均速度为 =3×0.02(25.0×10-3) m/s≈0.42 m/s.对描述B点的瞬时速度来说,AC段所取的位移间隔更小,更能接近B点的真实速度,即B点的瞬时速度更接近于0.35 m/s.
4、如图所示,打点计时器所用电源的频率为50 Hz,某次实验中得到一条纸带,用毫米刻度尺测出各点间的距离如图所示,则:AC=______mm,AD=_______ mm.那么由此可以算出纸带在AC间的平均速度为________ m/s,纸带在AD间的平均速度为________m/s;B点的瞬时速度更接近于________ m/s.
14.0
25.0
0.35
0.42
0.35
5、某同学在做“练习使用打点计时器”实验时打出的纸带如图所示,每两点之间还有四个点没有画出来,图中上面的数字为相邻两点间的距离,打点计时器的电源频率为50 Hz.
(1)相邻两个计数点间的时间为________ s.
(2)打第4个计数点时纸带的速度v4=________ m/s.(保留三位有效数字)
解析:(1)每两个计数点间有5个打点间隔,所以T=5×0.02 s=0.1 s.
(2)打第4个计数点时的瞬时速度近似等于3、5两点间的平均速度,所以
0.1
1.20
谢谢
大家
第 3 节 位置变化快慢的描述——速度
第一章 运动的描述
1.理解速度的物理意义,知道速度是矢量.
2.理解平均速度和瞬时速度的区别,知道速率的概念.
3.会用平均速度公式进行相关的计算.
教学目标
生活和科学研究中经常需要知道物体运动的快慢和方向。不同的运动,快慢程度并不相同。同学们猜想下是汽车快还是飞机快?
情景引入
A
B
O
1
5
cm
Δt=4s
xA=1cm
xB=5cm
O
100
500
m
Δt=10s
xC=100m
C
D
Δx= xB- xA=4cm
xD=500m
Δx = xD- xC=400m
速度
如何比较物体运动的快慢呢?
可以用单位时间内的位移来表示运动的快慢
1、定义:物理学中用位移与发生这段位移所用时间之比表示物体运动的快慢,这就是速度。
2、定义式:
3、物理意义:描述物体位置变化快慢和方向的物理量。
速度越大,位置变化越快,运动越快
4、单位:m/s(还有km/h、cm/s)
单位的换算
x ——位置
Δx ——位置变化大小——位置变化量
——位置变化快慢——位置变化率
——位移
——速度
5、速度是矢量:
大小:数值上等于单位时间内位移的大小。
方向:物体运动的方向。
6、比值定义法:用两个物理量的比值来定义一个新的物理量,这个新物理量与前两个物理量不直接成比例关系。
思考:两辆汽车从某地出发,速度都是20m/s,他们的运动情况完全相同吗?
可能是背道而驰 !!
v与Δx、Δt不直接成比例关系
注意:这里的速度和初中所学速度的含义不完全相同。
1、关于几个物理量的的说法正确的是( )
A.速度越大,物体的位移越大
B.速度越大,物体的位置变化越大
C.速度越大,物体的位置变化越快
D.速度越大,物体在单位时间内的位移越大
CD
课堂训练
2、关于速度的说法,下列各项中正确的是( )
A.速度是描述物体运动快慢的物理量,速度大表示物体运动的快
B.速度描述物体的位置变化快慢,速度大的表示物体位置变化大
C.速度越大,位置变化越快,位移也就越大
D.v1=2m/s,v2=-3m/s,v1表示的速度大
A
1、平均速度:
定义:物体在时间Δt内运动的平均快慢程度。运动物体的位移Δx与发生这段位移所用时间Δt的比值。
公式:
物理意义:粗略描述物体在时间Δt内运动的快慢和方向。
平均速度是矢量,既有大小又有方向。
方向:与Δx的方向相同,由初位置指向末位置。
平均速度和瞬时速度
求平均速度必须指明是求哪段时间(或哪段位移)的平均速度。
Δx与Δt的同一性和对应性
例1、做单向直线运动的一辆自行车在第一个5s内的位移为10m,第二个5s内的位移为15m,第三个5s内的位移为12m,第四个5s内的位移为15m。请分别求出它在每个5s内的平均速度以及这20s内的平均速度 第二个5s内的运动情况和第4个5s内的运动情况一定完全一样吗?
v1=2m/s;v2=3m/s;v3=2.4m/s;v4=3m/s;v=2.6m/s
例2、物体沿一条直线由A运动到B,
(1)若前1/3时间做速度为v1的匀速运动,后2/3时间做速度为v2的匀速运动,求物体从A到B的平均速度。
(2)若前1/3位移做速度为v1的匀速运动,后2/3位移做速度为v2的匀速运动,求物体从A到B的平均速度。
平均速度不是速度的平均值
t
(t+Δt )
可用时刻 t 到 t +Δt 一小段时间内的平均速度 来代替时刻 t 物体的速度,Δt 越小,运动快慢的差异就越小。当 Δt 非常非常小时,运动快慢的差异可以忽略不计,就可认为是t时刻的速度。
Δx
思考讨论:平均速度描述物体在一段时间内运动的平均快慢程度及方向。那么,怎样描述物体在某一时刻运动的快慢和方向呢?
2、瞬时速度
(1)定义:物体经过某一位置或在某一时刻的运动快慢程度就是瞬时速度。
(2)物理意义:瞬时速度精确地描述了物体运动的快慢。
(3)瞬时速度是矢量,既有大小又有方向。
方向:与物体在某一时刻或某一位置的运动方向相同。
大小:叫做瞬时速率、即时速率,简称速率。
(4)匀速直线运动是瞬时速度保持不变的运动。
在匀速直线运动中,平均速度与瞬时速度相等。
汽车速度计不能显示车辆运动的方向,它的示数实际是汽车的速率。
注意:日常生活中说到的“速度”,有时是指速率,要根据上下文判断。
例3、利用如图所示装置可以测量滑块从木板上下滑时通过光电门的速度。图中MN是水平桌面,PQ是木板,1和2是固定在木板上适当位置的两个光电门(与之连接的两个光电计时器没有画出)。让滑块从木板的顶端滑下,光电门1、2各自连接的计时器显示的挡光时间分别为5.0×10-2s和2.0×10-2s。小滑块的宽度d为0.5cm,则滑块通过光电门1的速度v1= ______m/s,滑块通过光电门2的速度v2= ______m/s。(结果保留两位有效数字)
0.10
0.25
3、下面的几个速度中表示瞬时速度的是 。
A.百米赛跑的运动员以9.5 m/s的速度冲过终点线
B.汽车从甲站行驶到乙站的速度是40 km/h
C.某同学从家里到学校步行速度为1.5 m/s
D.经提速后某动车的运行速度最高可达486 km/h
E.由于堵车,在隧道内的车速仅为1.2 m/s
F.返回地面的太空舱以8 m/s的速度落入太平洋中
G.汽车以72 km/h的速度通过长江大桥全程
H.子弹射出枪口的速度是800 m/s
I.小球第3 s末的速度是6 m/s
ADFHI
课堂训练
测量平均速度 用手拉通过打点计时器的纸带时,纸带运动确定时间内的位移就被记录下来,据此可以计算纸带运动的速度。
如图是打点计时器打出的一条纸带示意图。若想计算实验时运动纸带在D、G两点的
平均速度,只需测出D、G间的位移Δx和所用时间Δt,就可以算出平均速度:
计算每隔0.1s的平均速度纸带示意图
实验:测量纸带的平均速度和瞬时速度
每隔0.1s(或更短)计算一次平均速度。
1. 在图中选取纸带上一点为起始点0,后面每5个点取一个计数点,分别用数字1,2,3,...标出这些计数点;
2. 测量各计数点到起始点0的距离x,记录在表1中;
3. 计算两相邻计数点间的位移Δx 同时记录对应的时间Δt ;
4. 根据Δx和Δt计算纸带在相邻计数点间的平均速度v 。
位置 0 1 2 3 4 ...
x/m
Δx /m
Δt /s
v/(m/s)
表1 手拉纸带的位移和平均速度
测量瞬时速度 下面考虑如何测量图中E点的瞬时速度。
E点在D、G两点之间,D、G两点间的平均速度也可以求出。如果不要求很精确,用这个平均速度粗略地代表E点的瞬时速度,也未尝不可,如果把包含E点在内的间隔取得小一些,例如取图中的DF线段,那么经过D、F两点所用的时间Δt就会变短,用两点间位移Δx和时间Δt算出的平均速度代表纸带在E点瞬时速度,就会精确一些。D、F两点离E点越近,算出的平均速度越接近E点的瞬时速度。
D、F两点间的距离过小,测量误差会增大。所以实际测量过程中要根据需要及所用仪器的情况,在要测量的点附近选取合适的位移和时间。请考虑此实验中产生误差的原因。
思考:此实验中产生误差的原因有哪些?
请根据上述测量瞬时速度的方法,计算上节实验中纸带上各级计数点的瞬时速度。 每隔0.06s计算一次速度。
1. 从纸带起始点0算起,后面每3个点取一个计数点;
2. 测量各计数点到起始点0的距离x,记录在表2中;
3. 计算两相邻计数点间的位移 Δx,同时记录对应的时间Δt;
4. 根据Δx和Δt算出的速度值就可以代表在Δx这一区间内任意一点的瞬时速度。
将算出的各计数点的速度值记录在下表中。
计算每隔0.06s的平均速度纸带示意图
位置 0 1 2 3 4 ...
x/m
Δx /m
Δt /s
v/(m/s)
表2 手拉纸带各计数点的瞬时速度
(1)建立坐标系:以时间t为横轴,速度v为纵轴;
(2)描点;
(3)用平滑的曲线连起来。
v/(m·s-1)
t/s
O
作图步骤:
速度—时间图像或v-t图像
物体运动的速度随时间变化的情况可以用图来直观表示。以时间t横轴,速度v为纵轴,坐标中的图像为速度—时间图像或v-t图像。
速度-时间(v-t)图象
t/s 0 1 2 3 4 5 6 7
v m/s 0.05 0.10 0.20 0.30 0.28 0.28 0.46 0.55
0 1 2 3 4 5 6 7
0.6
0.5
0.4
0.3
0.2
0.1
t/10-1s
v/(m·s-1)
用图像表示速度
4、如下图是一个物体运动的v-t图象,从以下三个方面说明它的速度是怎样变化的.
(1)物体是从静止开始运动还是具有一定的初速度?
(2)运动的方向是否变化?
(3)速度的大小是否变化?怎样变化?
答案:(1)具有一定的初速度;
(2)运动方向在t3时刻发生变化;
(3)0~t1时间段内,速度均匀增大;t1~t2时间段内,速度不变;
t2~t3时间段内,速度均匀减小;t3时刻后,速度反向均匀增加。
课堂训练
1、物理学中用位移与发生这段位移所用时间之比表示物体速度。
2、速度是矢量,它既有大小,又有方向。 v的方向是由对应Δt时间内位移Δx的方向决定。
3、平均速度:粗略地描述了物体运动快慢程度和方向。
4、瞬时速度精确地描述了物体运动的快慢和方向。
5、测量纸带的平均速度和瞬时速度。
6、速度—时间图像。
课堂总结
1、 (多选)如图所示,一人骑自行车晨练,由静止开始沿直线运动,她在第1 s内、第2 s内、第3 s内、第4 s内通过的位移分别为1 m、2 m、3 m、4 m,则( )
A.她在4 s末的瞬时速度为4 m/s
B.她在第2 s内的平均速度为2 m/s
C.她在4 s内的平均速度为2.5 m/s
D.她在1 s末的速度为1 m/s
BC
解析:由 可得该人在第2s内的平均速度为2m/s,B正确;前4s内的平均速速
为 m/s=2.5m/s,C正确;因无法确定该人的瞬时速度,A、D错误。
跟踪练习
2、在110 m跨栏比赛中,某运动员用了13.15秒跑完全程。通过测量,测得他在5秒末的速度是8.00 m/s,到达终点的速度是9.80 m/s,则以下有关平均速度和瞬时速度的说法中正确的是( )
A.8.00 m/s是瞬时速度
B.9.80 m/s是全程的平均速度
C.全程的平均速度是8.90 m/s
D.全程的平均速度是8.37 m/s
AD
3、物体沿直线运动,下列说法中正确的是( )
A.物体在某时刻的速度为3 m/s,则该物体在1 s内的位移一定是3 m
B.物体在某1 s内的平均速度为3 m/s,则物体在这1 s内的位移一定是3 m
C.物体在某段时间内的平均速度为3 m/s,则物体在第1 s内的位移一定是3 m
D.物体在某段时间内的平均速度为3 m/s,则物体在任意1 s内的位移一定是3 m
B
Δx与Δt的同一性和对应性
解析:AC=14.0 mm,AC间的平均速度为 =2×0.02(14.0×10-3) m/s=0.35 m/s;AD=25.0 mm,AD间的平均速度为 =3×0.02(25.0×10-3) m/s≈0.42 m/s.对描述B点的瞬时速度来说,AC段所取的位移间隔更小,更能接近B点的真实速度,即B点的瞬时速度更接近于0.35 m/s.
4、如图所示,打点计时器所用电源的频率为50 Hz,某次实验中得到一条纸带,用毫米刻度尺测出各点间的距离如图所示,则:AC=______mm,AD=_______ mm.那么由此可以算出纸带在AC间的平均速度为________ m/s,纸带在AD间的平均速度为________m/s;B点的瞬时速度更接近于________ m/s.
14.0
25.0
0.35
0.42
0.35
5、某同学在做“练习使用打点计时器”实验时打出的纸带如图所示,每两点之间还有四个点没有画出来,图中上面的数字为相邻两点间的距离,打点计时器的电源频率为50 Hz.
(1)相邻两个计数点间的时间为________ s.
(2)打第4个计数点时纸带的速度v4=________ m/s.(保留三位有效数字)
解析:(1)每两个计数点间有5个打点间隔,所以T=5×0.02 s=0.1 s.
(2)打第4个计数点时的瞬时速度近似等于3、5两点间的平均速度,所以
0.1
1.20
谢谢
大家
