3.3探索与表达规律同步练习(含解析)北师大版数学七年级上册
文档属性
| 名称 | 3.3探索与表达规律同步练习(含解析)北师大版数学七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 15:39:08 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
3.3探索与表达规律
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.少数民族服饰以其精美的花纹和艳丽的色彩越来越受到设计师们的喜爱.某民族服饰的花边均是由基础图形进行若干次平移后组成的有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,第3个图案由10个基础图形组成,……,如图,按此规律排列下去,第2025个图案中的基础图形个数为( )
A.6070 B.6073 C.6076 D.6079
2.如图中每个图形都是由口、O、△中的两个(可以相同)构成.观察各图形与它下面的数之间的关系,可知最右面图形下面的“?”表示( )
A.23 B.32 C.13 D.31
3.小明的身份证号是,则他的出生年月是( )
A.2008年3月 B.2004年8月
C.2008年8月 D.2024年8月
4.按一定规律排列的多项式:,,,,,,,第10个多项式是( )
A. B. C. D.
5.如图,下列图形是由同样大小的棋子按照一定规律排列而成的,其中,图①中有5颗棋子,图②中有8颗棋子,图③中有13颗棋子,图④中有20颗棋子,按照此规律排列下去,图⑧中的棋子颗数为( )
A.55 B.68 C.72 D.85
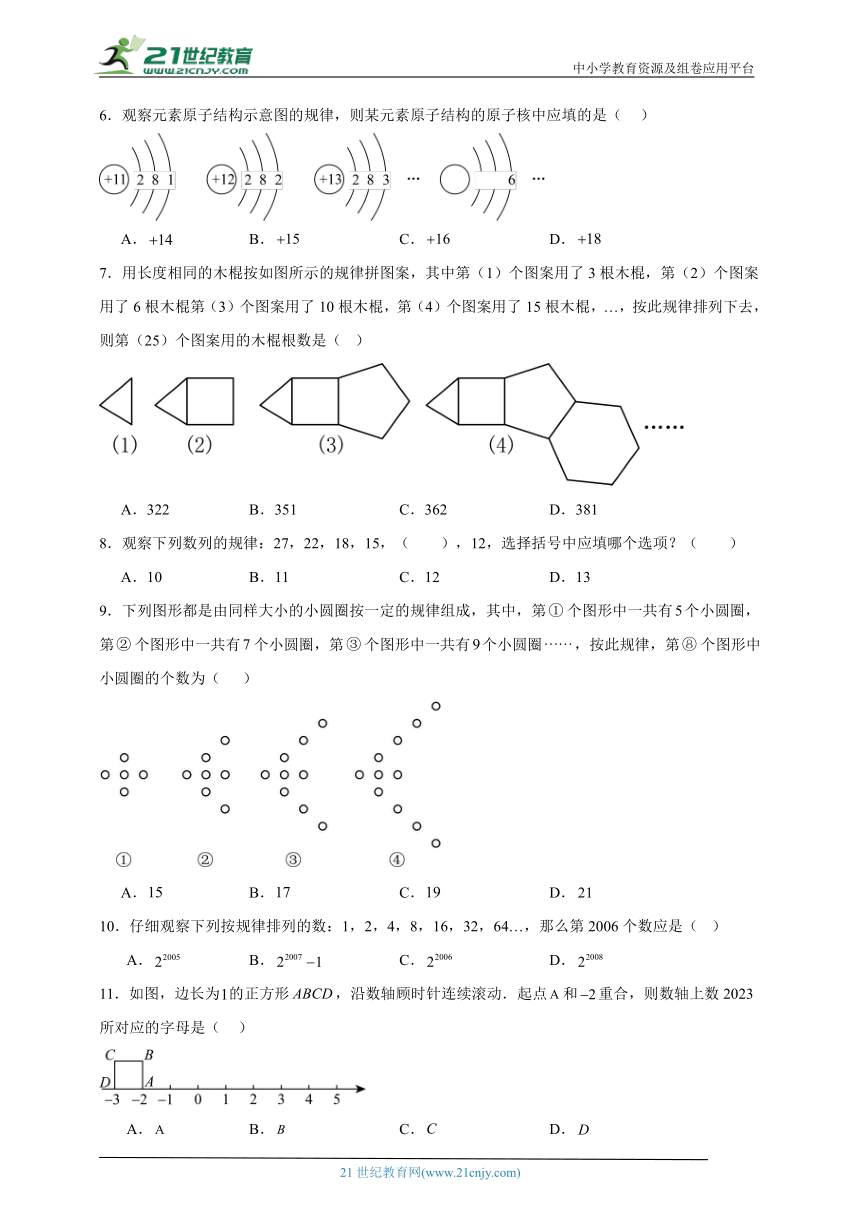
6.观察元素原子结构示意图的规律,则某元素原子结构的原子核中应填的是( )
A. B. C. D.
7.用长度相同的木棍按如图所示的规律拼图案,其中第(1)个图案用了3根木棍,第(2)个图案用了6根木棍第(3)个图案用了10根木棍,第(4)个图案用了15根木棍,…,按此规律排列下去,则第(25)个图案用的木棍根数是( )
A.322 B.351 C.362 D.381
8.观察下列数列的规律:27,22,18,15,( ),12,选择括号中应填哪个选项?( )
A.10 B.11 C.12 D.13
9.下列图形都是由同样大小的小圆圈按一定的规律组成,其中,第个图形中一共有个小圆圈,第个图形中一共有个小圆圈,第个图形中一共有个小圆圈,按此规律,第个图形中小圆圈的个数为( )
A. B. C. D.
10.仔细观察下列按规律排列的数:1,2,4,8,16,32,64…,那么第2006个数应是( )
A. B. C. D.
11.如图,边长为的正方形,沿数轴顾时针连续滚动.起点和重合,则数轴上数2023所对应的字母是( )
A. B. C. D.
12.同学们做操,排成一个正方形的队伍,从前、后、左、右数,小红都是第5个,问一共有( )人.
A.81 B.25 C.32 D.120
二、填空题
13.如图,线段上的点数与线段的总数有如下关系:当线段上有个点时,线段总共有条;当线段上有个点时,线段总共有条;当线段上有个点时,线段总共有条,···,按此规律.当线段上有个点时,线段总共有 条
14.观察下图,图(1)有2个三角形,记作;图(2)有3个三角形,记作;图(3)有6个三角形,记作;图(4)有11个三角形,记作;按此方法继续下去,则 (结果用含的代数式表示).
15.如图,在数轴上,、P两点表示的数分别是1、2,、关于点O对称,、关于点P对称,、关于点O对称,、关于点P对称……依此规律,则点表示的数是 .
16.(《时代学习报》数学文化节试题)东方传统建筑中的塔,千姿百态,造型各异.数学中的宝塔更是千变万化、不计其数.从1开始的奇数,按照规律排成下面形式的宝塔:
观察行中各数的规律:
前2行的各数之和;
前3行的各数之和;
前4行的各数之和;
前5行的各数之和;
因此,可推知前6行的各数之和 ;
根据以上规律,猜想: .
17.观察下列式子的规律:、、、、…,则第个式子为 .
三、解答题
18.观察以下等式:
第1个等式:,
第2个等式:,
第3个等式:,
第4个等式:,…
根据以上规律,解决下列问题:
(1)写出第5等式:______________;
(2)写出你猜想的第n个等式(用含n的等式表示),并说明其正确性.
19.阅读材料:
在计算时,直接计算很繁琐,我们可以采用“裂项——消项”法简化运算.
.
方法应用:试用“裂项—消项”法解下面各题:
(1);
(2).
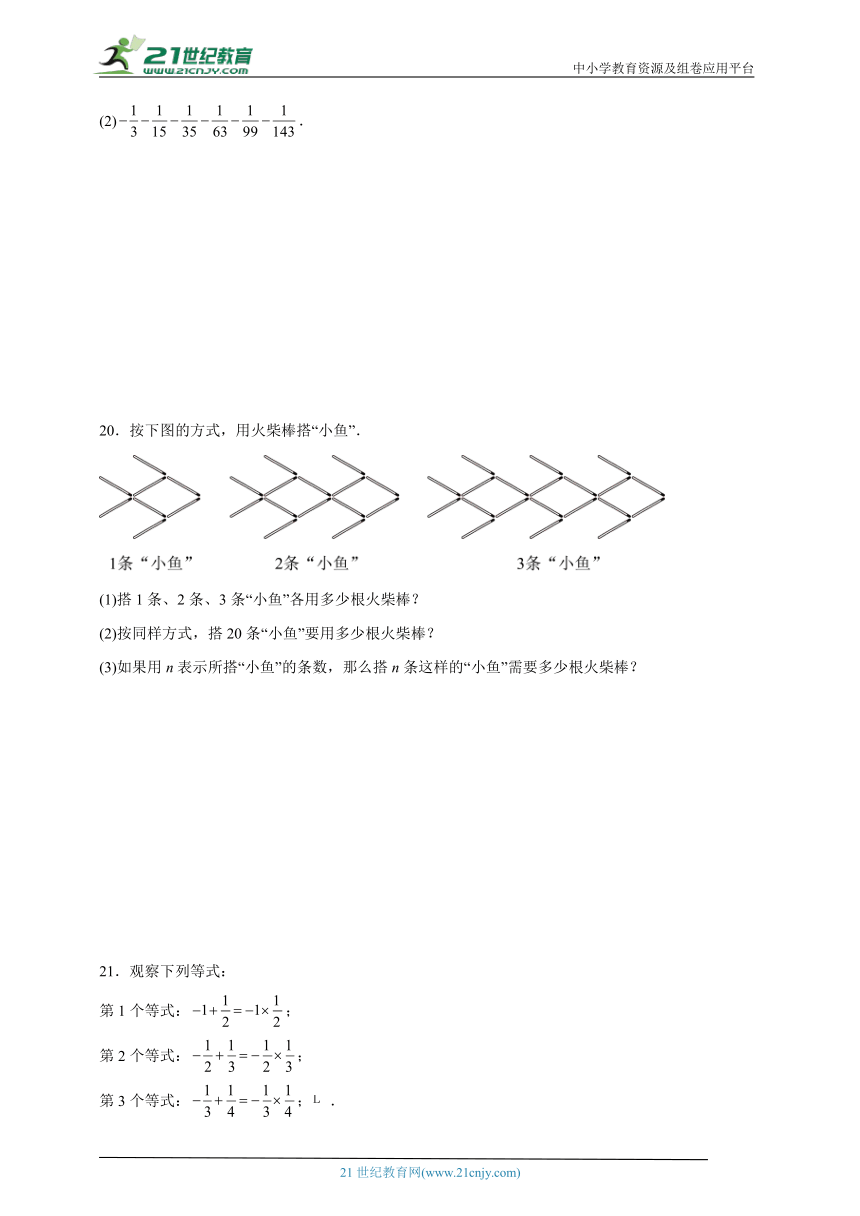
20.按下图的方式,用火柴棒搭“小鱼”.
(1)搭1条、2条、3条“小鱼”各用多少根火柴棒?
(2)按同样方式,搭20条“小鱼”要用多少根火柴棒?
(3)如果用n表示所搭“小鱼”的条数,那么搭n条这样的“小鱼”需要多少根火柴棒?
21.观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:;.
….
(1)请写出第5个等式:______;
(2)写出第个等式:______;(用含n的式子表示,n为正整数)
(3)根据你发现的规律计算:.
22.先阅读,再答题
根据你发现的规律,试写出:
(1);
(2)________________;
(3)计算:
23.如图,用棋子摆出一组形如正方形的图形,按照这种方法摆下去,摆第n个图形需要多少枚棋子?
24.如图,通过观察,小明同学发现可以用这样的方法确定每个图形中黑色和白色小正方形的总个数:如第1个图中共有1个黑色小正方形,第2个图中共有个黑白小正方形,第3个图中共有个黑白小正方形.第4个图中共有个黑白小正方形,回答问题:
(1)根据规律,第5个图中计算黑白小正方形的等式是: ;
(2)根据规律,第个图中计算黑白小正方形的等式是: ;
(3)根据(2)的等式,计算:.
《3.3探索与表达规律》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C B B C B D C A
题号 11 12
答案 B A
1.C
【分析】本题考查了图形类规律探索,根据图形找出已知规律是解题关键.观察图形发现第个图案由个基础图形组成,即可求解.
【详解】解:由图形可知,第1个图案由4个基础图形组成,,
第2个图案由7个基础图形组成,,
第3个图案由10个基础图形组成,,
……
观察发现,第个图案由个基础图形组成,
第2025个图案中的基础图形个数为,
故选:C.
2.D
【分析】本题为图形规律题,合理分析变化规律是解题的关键.
观察图形找出规律求解即可.
【详解】
解:观察可得:两个三角形,一内一外,即三角形代表;
观察可得:一内一外,即正方形代表,圆型代表;
观察可得:一内一外,即三角形代表,正方形代表;
观察可得:一内一外,即圆型代表;
综上一内一外,内部圆形为,外部正方形为,则此图为;
故选:D.
3.C
【分析】本题是考查身份证的数字编码问题,身份证的第位表示的出生日期,其中位是出生的年份,11、12位是出生的月份,据此解答.
【详解】解:小明的身份证号是,则他的出生年月是2008年8月.
故选:C.
4.B
【分析】本题考查了数字规律,理解材料提示,找出规律是关键.
根据材料提示,找出多项式的各项系数,指数的规律即可求解.
【详解】解:多项式:,,,,,,,
∴的系数是(是正整数),奇数项的符号为正,偶数项的符号为负,的指数为(是正整数),
∴当时,的系数是,的符号为负,的指数为,
∴第10个多项式是,
故选:B .
5.B
【分析】本题考查了图形的变化规律,根据题意得出第n个图形中棋子数为,据此求解.
【详解】解:图①数量是,
图②数量是,
图③数量是,
图④数量是,
,
图n中棋子的数量是,
当时,,
故选:B.
6.C
【分析】本题主要考查了数字规律.
通过观察三种原子结构示意图的电子分布规律发现原子核外电子的电子数之和等于原子核中的数字,据此即可解答.
【详解】解:由三种原子结构示意图可知:原子核外电子排布为第一层2个,第二层8个,三个电子层的电子数之和等于原子核中的数字.
故:该元素原子结构的原子核中数字,
故选C.
7.B
【分析】本题主要考查了图形变化的规律,根据所给图形,依次求出所需木棍的根数,发现规律即可解决问题.
【详解】解:由所给图形可知,
第(1)个图案所用木棍的根数为:;
第(2)个图案所用木棍的根数为:;
第(3)个图案所用木棍的根数为:;
…,
所以第()个图案所用木棍的根数为:.
当时,(根),
即第(25)个图案所用木棍的根数为351根.
故选:B.
8.D
【分析】本题考查数字变化的规律,根据所给数列发现前后两数的差依次减少1是解题的关键.
观察所给数列发现前后两数的差依次减少1,据此可解决问题.
【详解】解:由题知,
,
,
,
∴接下来两数的差为2,
则,
且,
符合此规律,
∴括号中应填13.
故选:D.
9.C
【分析】本题主要考查图形规律,理解图示数量关系,找出规律是关键.
根据图示的数量得到第个图形中一共有个小圆圈,由此即可求解.
【详解】解:由题知,第①个图形中一共有个小圆圈,
第②个图形中一共有个小圆圈,
第③个图形中一共有个小圆圈,
,
∴第个图形中一共有个小圆圈,
∴第⑧个图形中小圆圈的个数为,
故选:C.
10.A
【分析】认真观察各数,发现数与数之间的变化规律,把各数写成乘方的形式是此题的关键.因为、、、、、可得出规律:、、、、、、.
【详解】解:,
第2006个数应是.
故选:A.
11.B
【分析】本题考查旋转正方形所对应的数问题,掌握旋转正方形对应四个数规律,发现规律,用规律解决问题是关键.
【详解】旋转1次B在位置,第2次旋转点C在0位置,第3次旋转点D在1位置,第4次旋转点A在2位置,第5次旋转B在3位置,
,
,
数轴上2023所对应的点是B点.
故答案为:B.
12.A
【分析】此题考查了方阵问题中总点数每边点数每边点数的灵活应用,关键是根据行、列排列特点求出每边人数.
因为从前、后、左、右数,小红都是第5个,所以每行都有:人,由此利用方阵问题中:总人数每边人数每边人数,即可解答.
【详解】解:每边人数是:(人),
共有:(人),
答:一共有81人.
故选:A.
13.
【分析】本题考查线段条数计算和规律性探索,解答关键是辨别线段数目增长的规律.
根据给出的条件进行观察找出规律:当有个点时,线段总共有条,代入,即可求解.
【详解】解:∵当线段上有个点时,线段总共有条;
当线段上有个点时,线段总共有条;
当线段上有个点时,线段总共有条,
···,按此规律.
∴当线段上有个点时,线段总共有条,
∴当线段上有个点时,线段总共有条,
故答案为:条.
14.
【分析】本题考查了图形的变化类问题,解决此类探究性问题,关键在观察、分析已知数据,寻找它们之间的共同规律以及与第一个图形的相互联系,探寻其规律.仔细观察图形变化,找到图形的变化规律,利用规律解题即可.
【详解】解:第一个图形中有个三角形;
第二个图形中有个三角形;
第三个图形中有个三角形;
第四个图形中有个三角形;
;
第n个图形中有个三角形.
故答案为:
15.
【分析】木题考查了数字的规律,找出一般规律是解题的关键;由已知条件找出关于:,:,:,:,:,根据对称规律得、关于点O对称,即可求解.
【详解】解:,P两点表示的数分别是1,2,、关于点O对称,
表示的数是,
,关于点P对称,
表示的数是,
同理可得::,:,:,:,:,
根据对称规律得、关于点O对称,
点表示的数是,
故答案为:.
16.
【分析】本题主要考查了数字类的规律探索,观察可知连续几个数的立方和等于这几个数的和的平方,据此规律求解即可.
【详解】解:前2行的各数之和
前3行的各数之和;
前4行的各数之和;
前5行的各数之和,
前6行的各数之和
……,
以此类推可得,
故答案为:;.
17.
【分析】本题考查了数字规律,理解式子中系数,字母指数的数量关系是关键.
根据式子中系数,字母指数的数字规律即可求解.
【详解】解:、、、、…,
系数依次是,字母的指数依次是,
∴第个式子为,
故答案为: .
18.(1)
(2)
【分析】本题考查有理数混合运算的规律探索,正确理解题意是解题的关键.
根据题目给出的4个等式,找到规律,即可解答.
【详解】(1)解:根据规律,第5等式为,
故答案为.
(2)第1个等式:,
第2个等式:,
第3个等式:,
第4个等式:,…
根据以上规律,第n个等式为.
故答案为.
19.(1)
(2)
【分析】本题考查了数字的变化类,找到变化规律是解题的关键.
(1)根据题中的方法,进行“裂项——消项”法简化运算;
(2)根据题中的方法,进行“裂项——消项”法简化运算.
【详解】(1)解:
;
(2)解:
.
20.(1)搭1条,2条,3条“小鱼”各用8根,14根,20根火柴棒
(2)按同样方式,搭20条“小鱼”要用122根火柴棒
(3)搭n条这样的“小鱼”需要根火柴棒
【分析】本题考查了图形的变化类问题,对于找规律的题目首先应找出发生变化的位置,并且观察变化规律,注意由特殊到一般的分析方法.
(1)根据题干内容求解即可;
(2)找出规律,得出搭20条这样的小鱼需要的火柴根数即可;
(3)根据规律,总结出公式即可.
【详解】(1)搭第1条小鱼需要的火柴棒个数为:;
搭第2条小鱼需要的火柴棒个数为:;
搭第3条小鱼需要的火柴棒个数为:;
(2)由(1)得,搭第20条小鱼需要的火柴棒个数为:;
(3)由(1)得,搭第n条小鱼需要的火柴棒个数为:.
21.(1)
(2)
(3)
【分析】本题考查了数字类规律题,有理数的四则混合运算,掌握数字类规律是解题的关键.
(1)根据规律计算即可求解;
(2)根据规律即可求解;
(3)先将乘法化为加法,再加减即可求解;
【详解】(1)解:第5个等式:,
故答案为:;
(2)解:第n个等式:,
故答案为:;
(3)解:原式.
.
22.(1)9;11
(2)
(3)
【分析】本题考查数字规律的探索,结合题意分析规律是解题的关键.
(1)根据题中规律得出第5个等式即可得出结果;
(2)根据题意总结出规律即可;
(3)结合(2)中规律求解即可.
【详解】(1)解:由题意可得,第5个等式为,
故答案为:9;11;
(2)由题意可得,第n个等式:,
故答案为:
(3)
,
.
23.
【分析】本题主要考查了图形类的规律探索,观察前3个图形可知每个图形需要的棋子数为序号的4倍,据此规律求解即可.
【详解】解:第1个图形需要枚棋子,
第2个图形需要枚棋子,
第3个图形需要枚棋子,
……,
以此类推,可知第 n 个图形需要枚棋子.
24.(1)
(2)
(3)7500
【分析】本题考查了图形的变化规律、有理数混合运算,熟练掌握以上知识点是关键.
(1)根据各图形中小正方形个数的变化可找出变化规律即可求出结论;
(2)根据各图形中小正方形个数的变化可找出变化规律“第n个图形中有小正方形的个数即可求解;
(3)利用(2)的规律即可求解.
【详解】(1)解:第1个图中,计算黑白小正方形的等式是:;
第2个图中,计算黑白小正方形的等式是:;
第3个图中,计算黑白小正方形的等式是:;
第4个图中,计算黑白小正方形的等式是:;
第5个图中,计算黑白小正方形的等式是:
故答案为:
(2)解:由(1)得:;
故答案为:
(3)解:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.3探索与表达规律
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.少数民族服饰以其精美的花纹和艳丽的色彩越来越受到设计师们的喜爱.某民族服饰的花边均是由基础图形进行若干次平移后组成的有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,第3个图案由10个基础图形组成,……,如图,按此规律排列下去,第2025个图案中的基础图形个数为( )
A.6070 B.6073 C.6076 D.6079
2.如图中每个图形都是由口、O、△中的两个(可以相同)构成.观察各图形与它下面的数之间的关系,可知最右面图形下面的“?”表示( )
A.23 B.32 C.13 D.31
3.小明的身份证号是,则他的出生年月是( )
A.2008年3月 B.2004年8月
C.2008年8月 D.2024年8月
4.按一定规律排列的多项式:,,,,,,,第10个多项式是( )
A. B. C. D.
5.如图,下列图形是由同样大小的棋子按照一定规律排列而成的,其中,图①中有5颗棋子,图②中有8颗棋子,图③中有13颗棋子,图④中有20颗棋子,按照此规律排列下去,图⑧中的棋子颗数为( )
A.55 B.68 C.72 D.85
6.观察元素原子结构示意图的规律,则某元素原子结构的原子核中应填的是( )
A. B. C. D.
7.用长度相同的木棍按如图所示的规律拼图案,其中第(1)个图案用了3根木棍,第(2)个图案用了6根木棍第(3)个图案用了10根木棍,第(4)个图案用了15根木棍,…,按此规律排列下去,则第(25)个图案用的木棍根数是( )
A.322 B.351 C.362 D.381
8.观察下列数列的规律:27,22,18,15,( ),12,选择括号中应填哪个选项?( )
A.10 B.11 C.12 D.13
9.下列图形都是由同样大小的小圆圈按一定的规律组成,其中,第个图形中一共有个小圆圈,第个图形中一共有个小圆圈,第个图形中一共有个小圆圈,按此规律,第个图形中小圆圈的个数为( )
A. B. C. D.
10.仔细观察下列按规律排列的数:1,2,4,8,16,32,64…,那么第2006个数应是( )
A. B. C. D.
11.如图,边长为的正方形,沿数轴顾时针连续滚动.起点和重合,则数轴上数2023所对应的字母是( )
A. B. C. D.
12.同学们做操,排成一个正方形的队伍,从前、后、左、右数,小红都是第5个,问一共有( )人.
A.81 B.25 C.32 D.120
二、填空题
13.如图,线段上的点数与线段的总数有如下关系:当线段上有个点时,线段总共有条;当线段上有个点时,线段总共有条;当线段上有个点时,线段总共有条,···,按此规律.当线段上有个点时,线段总共有 条
14.观察下图,图(1)有2个三角形,记作;图(2)有3个三角形,记作;图(3)有6个三角形,记作;图(4)有11个三角形,记作;按此方法继续下去,则 (结果用含的代数式表示).
15.如图,在数轴上,、P两点表示的数分别是1、2,、关于点O对称,、关于点P对称,、关于点O对称,、关于点P对称……依此规律,则点表示的数是 .
16.(《时代学习报》数学文化节试题)东方传统建筑中的塔,千姿百态,造型各异.数学中的宝塔更是千变万化、不计其数.从1开始的奇数,按照规律排成下面形式的宝塔:
观察行中各数的规律:
前2行的各数之和;
前3行的各数之和;
前4行的各数之和;
前5行的各数之和;
因此,可推知前6行的各数之和 ;
根据以上规律,猜想: .
17.观察下列式子的规律:、、、、…,则第个式子为 .
三、解答题
18.观察以下等式:
第1个等式:,
第2个等式:,
第3个等式:,
第4个等式:,…
根据以上规律,解决下列问题:
(1)写出第5等式:______________;
(2)写出你猜想的第n个等式(用含n的等式表示),并说明其正确性.
19.阅读材料:
在计算时,直接计算很繁琐,我们可以采用“裂项——消项”法简化运算.
.
方法应用:试用“裂项—消项”法解下面各题:
(1);
(2).
20.按下图的方式,用火柴棒搭“小鱼”.
(1)搭1条、2条、3条“小鱼”各用多少根火柴棒?
(2)按同样方式,搭20条“小鱼”要用多少根火柴棒?
(3)如果用n表示所搭“小鱼”的条数,那么搭n条这样的“小鱼”需要多少根火柴棒?
21.观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:;.
….
(1)请写出第5个等式:______;
(2)写出第个等式:______;(用含n的式子表示,n为正整数)
(3)根据你发现的规律计算:.
22.先阅读,再答题
根据你发现的规律,试写出:
(1);
(2)________________;
(3)计算:
23.如图,用棋子摆出一组形如正方形的图形,按照这种方法摆下去,摆第n个图形需要多少枚棋子?
24.如图,通过观察,小明同学发现可以用这样的方法确定每个图形中黑色和白色小正方形的总个数:如第1个图中共有1个黑色小正方形,第2个图中共有个黑白小正方形,第3个图中共有个黑白小正方形.第4个图中共有个黑白小正方形,回答问题:
(1)根据规律,第5个图中计算黑白小正方形的等式是: ;
(2)根据规律,第个图中计算黑白小正方形的等式是: ;
(3)根据(2)的等式,计算:.
《3.3探索与表达规律》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C B B C B D C A
题号 11 12
答案 B A
1.C
【分析】本题考查了图形类规律探索,根据图形找出已知规律是解题关键.观察图形发现第个图案由个基础图形组成,即可求解.
【详解】解:由图形可知,第1个图案由4个基础图形组成,,
第2个图案由7个基础图形组成,,
第3个图案由10个基础图形组成,,
……
观察发现,第个图案由个基础图形组成,
第2025个图案中的基础图形个数为,
故选:C.
2.D
【分析】本题为图形规律题,合理分析变化规律是解题的关键.
观察图形找出规律求解即可.
【详解】
解:观察可得:两个三角形,一内一外,即三角形代表;
观察可得:一内一外,即正方形代表,圆型代表;
观察可得:一内一外,即三角形代表,正方形代表;
观察可得:一内一外,即圆型代表;
综上一内一外,内部圆形为,外部正方形为,则此图为;
故选:D.
3.C
【分析】本题是考查身份证的数字编码问题,身份证的第位表示的出生日期,其中位是出生的年份,11、12位是出生的月份,据此解答.
【详解】解:小明的身份证号是,则他的出生年月是2008年8月.
故选:C.
4.B
【分析】本题考查了数字规律,理解材料提示,找出规律是关键.
根据材料提示,找出多项式的各项系数,指数的规律即可求解.
【详解】解:多项式:,,,,,,,
∴的系数是(是正整数),奇数项的符号为正,偶数项的符号为负,的指数为(是正整数),
∴当时,的系数是,的符号为负,的指数为,
∴第10个多项式是,
故选:B .
5.B
【分析】本题考查了图形的变化规律,根据题意得出第n个图形中棋子数为,据此求解.
【详解】解:图①数量是,
图②数量是,
图③数量是,
图④数量是,
,
图n中棋子的数量是,
当时,,
故选:B.
6.C
【分析】本题主要考查了数字规律.
通过观察三种原子结构示意图的电子分布规律发现原子核外电子的电子数之和等于原子核中的数字,据此即可解答.
【详解】解:由三种原子结构示意图可知:原子核外电子排布为第一层2个,第二层8个,三个电子层的电子数之和等于原子核中的数字.
故:该元素原子结构的原子核中数字,
故选C.
7.B
【分析】本题主要考查了图形变化的规律,根据所给图形,依次求出所需木棍的根数,发现规律即可解决问题.
【详解】解:由所给图形可知,
第(1)个图案所用木棍的根数为:;
第(2)个图案所用木棍的根数为:;
第(3)个图案所用木棍的根数为:;
…,
所以第()个图案所用木棍的根数为:.
当时,(根),
即第(25)个图案所用木棍的根数为351根.
故选:B.
8.D
【分析】本题考查数字变化的规律,根据所给数列发现前后两数的差依次减少1是解题的关键.
观察所给数列发现前后两数的差依次减少1,据此可解决问题.
【详解】解:由题知,
,
,
,
∴接下来两数的差为2,
则,
且,
符合此规律,
∴括号中应填13.
故选:D.
9.C
【分析】本题主要考查图形规律,理解图示数量关系,找出规律是关键.
根据图示的数量得到第个图形中一共有个小圆圈,由此即可求解.
【详解】解:由题知,第①个图形中一共有个小圆圈,
第②个图形中一共有个小圆圈,
第③个图形中一共有个小圆圈,
,
∴第个图形中一共有个小圆圈,
∴第⑧个图形中小圆圈的个数为,
故选:C.
10.A
【分析】认真观察各数,发现数与数之间的变化规律,把各数写成乘方的形式是此题的关键.因为、、、、、可得出规律:、、、、、、.
【详解】解:,
第2006个数应是.
故选:A.
11.B
【分析】本题考查旋转正方形所对应的数问题,掌握旋转正方形对应四个数规律,发现规律,用规律解决问题是关键.
【详解】旋转1次B在位置,第2次旋转点C在0位置,第3次旋转点D在1位置,第4次旋转点A在2位置,第5次旋转B在3位置,
,
,
数轴上2023所对应的点是B点.
故答案为:B.
12.A
【分析】此题考查了方阵问题中总点数每边点数每边点数的灵活应用,关键是根据行、列排列特点求出每边人数.
因为从前、后、左、右数,小红都是第5个,所以每行都有:人,由此利用方阵问题中:总人数每边人数每边人数,即可解答.
【详解】解:每边人数是:(人),
共有:(人),
答:一共有81人.
故选:A.
13.
【分析】本题考查线段条数计算和规律性探索,解答关键是辨别线段数目增长的规律.
根据给出的条件进行观察找出规律:当有个点时,线段总共有条,代入,即可求解.
【详解】解:∵当线段上有个点时,线段总共有条;
当线段上有个点时,线段总共有条;
当线段上有个点时,线段总共有条,
···,按此规律.
∴当线段上有个点时,线段总共有条,
∴当线段上有个点时,线段总共有条,
故答案为:条.
14.
【分析】本题考查了图形的变化类问题,解决此类探究性问题,关键在观察、分析已知数据,寻找它们之间的共同规律以及与第一个图形的相互联系,探寻其规律.仔细观察图形变化,找到图形的变化规律,利用规律解题即可.
【详解】解:第一个图形中有个三角形;
第二个图形中有个三角形;
第三个图形中有个三角形;
第四个图形中有个三角形;
;
第n个图形中有个三角形.
故答案为:
15.
【分析】木题考查了数字的规律,找出一般规律是解题的关键;由已知条件找出关于:,:,:,:,:,根据对称规律得、关于点O对称,即可求解.
【详解】解:,P两点表示的数分别是1,2,、关于点O对称,
表示的数是,
,关于点P对称,
表示的数是,
同理可得::,:,:,:,:,
根据对称规律得、关于点O对称,
点表示的数是,
故答案为:.
16.
【分析】本题主要考查了数字类的规律探索,观察可知连续几个数的立方和等于这几个数的和的平方,据此规律求解即可.
【详解】解:前2行的各数之和
前3行的各数之和;
前4行的各数之和;
前5行的各数之和,
前6行的各数之和
……,
以此类推可得,
故答案为:;.
17.
【分析】本题考查了数字规律,理解式子中系数,字母指数的数量关系是关键.
根据式子中系数,字母指数的数字规律即可求解.
【详解】解:、、、、…,
系数依次是,字母的指数依次是,
∴第个式子为,
故答案为: .
18.(1)
(2)
【分析】本题考查有理数混合运算的规律探索,正确理解题意是解题的关键.
根据题目给出的4个等式,找到规律,即可解答.
【详解】(1)解:根据规律,第5等式为,
故答案为.
(2)第1个等式:,
第2个等式:,
第3个等式:,
第4个等式:,…
根据以上规律,第n个等式为.
故答案为.
19.(1)
(2)
【分析】本题考查了数字的变化类,找到变化规律是解题的关键.
(1)根据题中的方法,进行“裂项——消项”法简化运算;
(2)根据题中的方法,进行“裂项——消项”法简化运算.
【详解】(1)解:
;
(2)解:
.
20.(1)搭1条,2条,3条“小鱼”各用8根,14根,20根火柴棒
(2)按同样方式,搭20条“小鱼”要用122根火柴棒
(3)搭n条这样的“小鱼”需要根火柴棒
【分析】本题考查了图形的变化类问题,对于找规律的题目首先应找出发生变化的位置,并且观察变化规律,注意由特殊到一般的分析方法.
(1)根据题干内容求解即可;
(2)找出规律,得出搭20条这样的小鱼需要的火柴根数即可;
(3)根据规律,总结出公式即可.
【详解】(1)搭第1条小鱼需要的火柴棒个数为:;
搭第2条小鱼需要的火柴棒个数为:;
搭第3条小鱼需要的火柴棒个数为:;
(2)由(1)得,搭第20条小鱼需要的火柴棒个数为:;
(3)由(1)得,搭第n条小鱼需要的火柴棒个数为:.
21.(1)
(2)
(3)
【分析】本题考查了数字类规律题,有理数的四则混合运算,掌握数字类规律是解题的关键.
(1)根据规律计算即可求解;
(2)根据规律即可求解;
(3)先将乘法化为加法,再加减即可求解;
【详解】(1)解:第5个等式:,
故答案为:;
(2)解:第n个等式:,
故答案为:;
(3)解:原式.
.
22.(1)9;11
(2)
(3)
【分析】本题考查数字规律的探索,结合题意分析规律是解题的关键.
(1)根据题中规律得出第5个等式即可得出结果;
(2)根据题意总结出规律即可;
(3)结合(2)中规律求解即可.
【详解】(1)解:由题意可得,第5个等式为,
故答案为:9;11;
(2)由题意可得,第n个等式:,
故答案为:
(3)
,
.
23.
【分析】本题主要考查了图形类的规律探索,观察前3个图形可知每个图形需要的棋子数为序号的4倍,据此规律求解即可.
【详解】解:第1个图形需要枚棋子,
第2个图形需要枚棋子,
第3个图形需要枚棋子,
……,
以此类推,可知第 n 个图形需要枚棋子.
24.(1)
(2)
(3)7500
【分析】本题考查了图形的变化规律、有理数混合运算,熟练掌握以上知识点是关键.
(1)根据各图形中小正方形个数的变化可找出变化规律即可求出结论;
(2)根据各图形中小正方形个数的变化可找出变化规律“第n个图形中有小正方形的个数即可求解;
(3)利用(2)的规律即可求解.
【详解】(1)解:第1个图中,计算黑白小正方形的等式是:;
第2个图中,计算黑白小正方形的等式是:;
第3个图中,计算黑白小正方形的等式是:;
第4个图中,计算黑白小正方形的等式是:;
第5个图中,计算黑白小正方形的等式是:
故答案为:
(2)解:由(1)得:;
故答案为:
(3)解:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
