2024-2025学年江苏省宿迁市钟吾初级中学八年级(下)月考数学试卷(3月份)(含部分答案)
文档属性
| 名称 | 2024-2025学年江苏省宿迁市钟吾初级中学八年级(下)月考数学试卷(3月份)(含部分答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 142.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 19:54:30 | ||
图片预览



文档简介
2024-2025学年江苏省宿迁市钟吾初级中学八年级(下)月考数学试卷(3月份)
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列图形既是中心对称图形,也是轴对称图形的是( )
A. B. C. D.
2.下列计算正确的是( )
A. B. C. D.
3.下列二次根式与是同类二次根式的是( )
A. B. C. D.
4.矩形具备但是平行四边形不一定具备的性质是( )
A. 两组对边分别相等 B. 两组对角分别相等
C. 两条对角线相等 D. 两条对角线互相平分
5.已知ab<0,且,,则a+b结果是( )
A. 8 B. 2 C. -2 D. -8
6.如图 ABCD,E,F分别是边AD,BC上的点,且AE=BF,连接AF与BE相交于点P,连接DF与CE相交于点Q,若S△ABP=3,S ABCD=36,则阴影部分的面积为( )
A. 15 B. 16 C. 17 D. 18
7.如图,将△ABC绕点A逆时针旋转60°得到△ADE,DE与BC交于点P,下列结论:①BC=DE;②PA平分∠BPE;③PA+PC=PE;④PA+PD=PB.其中正确的有( )
A. 1个
B. 2个
C. 3个
D. 4个
8.如图,在Rt△ABC中,∠BAC=90°,∠B=60°,AB=4,P为BC边上的动点,以PA,PC为邻边作 PAQC,连接PQ,则PQ长的最小值是( )
A. 2 B. 4 C. D.
二、填空题:本题共10小题,每小题3分,共30分。
9.函数的定义域是______.
10.比较大小: ______.(填“>”、“<”或“=”)
11.二次根式,,,,中是最简二次根式的是______.
12.已知,则= ______.
13.实数a,b在数轴上的位置如图所示,则化简的值是______.
14.对于任意两个不相等的正实数a,b,定义一种新运算“ ”,即,如,则6 8= ______.
15.如图,将矩形ABCD绕点A顺时针旋转到矩形AEFG的位置,已知∠1=110°,则旋转角α= ______.
16.如图矩形ABCD,点E在BC的延长线上,CE=BD,连接AE,如果∠E=28°,则∠ADB= ______.
17.如图 ABCD,∠ABC=135°,E在CD的延长线上,F在BC上,AE∥BD,EF⊥BC,已知EF=4,则AB的长是______.
18.整数x满足0<x<60,且二次根式与是同类二次根式,则x= ______.
三、解答题:本题共10小题,共96分。解答应写出文字说明,证明过程或演算步骤。
19.(本小题8分)
计算:
(1)×;
(2).
20.(本小题8分)
化简:
(1);
(2).
21.(本小题8分)
(1)已知x、y为实数,且,求的值;
(2)已知x+y=7,xy=8,求代数式x2+y2的值.
22.(本小题8分)
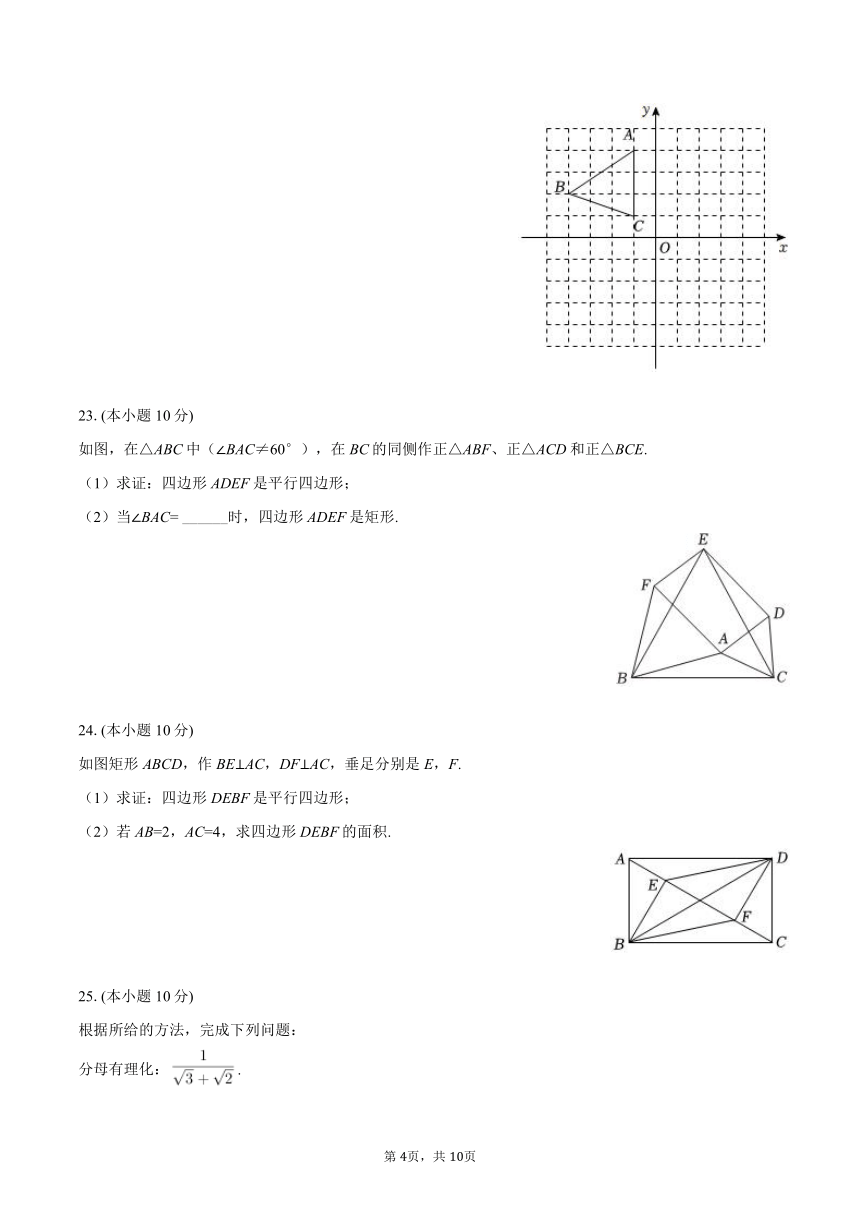
如图直角坐标系,网格中最小正方形的边长为1,已知△ABC.
(1)画出△ABC关于原点成中心对称的△A1B1C1;
(2)画出将△ABC绕坐标原点O逆时针旋转90°,得到△A2B2C2;
(3)请直接写出以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
23.(本小题10分)
如图,在△ABC中(∠BAC≠60°),在BC的同侧作正△ABF、正△ACD和正△BCE.
(1)求证:四边形ADEF是平行四边形;
(2)当∠BAC= ______时,四边形ADEF是矩形.
24.(本小题10分)
如图矩形ABCD,作BE⊥AC,DF⊥AC,垂足分别是E,F.
(1)求证:四边形DEBF是平行四边形;
(2)若AB=2,AC=4,求四边形DEBF的面积.
25.(本小题10分)
根据所给的方法,完成下列问题:
分母有理化:.
解:.
(1)计算:;
(2)已知,,求x2+y2的值.
26.(本小题10分)
在 ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明BE=CD;
(2)在图2中,若∠ABC=90°,G是EF的中点,求∠BDG的度数.
27.(本小题12分)
如图①,在平面直角坐标系中,已知 ABCD在第一象限,点A在y的正半轴,AB∥x轴.直线y=-x从原点出发沿x轴正方向向右平移,在平移过程中直线y=-x被 ABCD截得的线段长度l与直线在x轴上平移的距离m的函数图象如图②所示.
(1)直接写出点A,B的坐标:A ______,B ______;
(2)求点D的坐标;
(3)当直线y=-x平分 ABCD的面积时,m= ______.
28.(本小题12分)
如图正方形网格中最小正方形的边长都是1,每个小正方形的顶点称为格点, ABCD的顶点A、B、C、D都在格点上,只用无刻度的直尺,分别在给定的网格中按下列要求作图,保留作图痕迹.
(1) ABCD的面积为______;
(2)在图①中,画出 ABCD的边AD上的高BE,并求BE的长;
(3)在图②中,在 ABCD的边AD上找一点F,连结AF,使∠ABF=45°,并直接写出BF的长:______.
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】C
5.【答案】B
6.【答案】A
7.【答案】D
8.【答案】C
9.【答案】x>-2
10.【答案】<
11.【答案】
12.【答案】2
13.【答案】b
14.【答案】
15.【答案】20°
16.【答案】56°
17.【答案】2
18.【答案】3或23
19.【答案】3+2;
2-.
20.【答案】3;
m.
21.【答案】2;
14.
22.【答案】如图,△A1B1C1即为所求;
如图,△A2B2C2即为所求;
、
如图,D1(-4,5),D2(2,3),D3(-4,-1).
23.【答案】证明:∵△ABF、△ACD、△BCE都是正三角形,
∴AB=BF=AF,AC=CD=AD,BE=BC=CE,∠ABF=∠CBE=∠BCE=∠ACD=60°,
∴∠ABF-∠ABE=∠CBE-∠ABE,
即∠FBE=∠ABC,
在△FBE和△ABC中,
,
∴△FBE≌△ABC(SAS),
∴EF=AC,
同理:△DEC≌△ABC(SAS),
∴DE=AB,
∴DE=AB=AF,EF=AC=AD,
∴四边形ADEF是平行四边形;
150°.
24.【答案】证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,
∴∠BAE=∠DCF,
∵BE⊥AC,DF⊥AC,
∴BE∥DF,∠AEB=∠CFD=90°,
∴△AEB≌△CFD(AAS),
∴BE=DF,
∴四边形DEBF是平行四边形;
2.
25.【答案】9;
1.
26.【答案】(1)证明:如图1,∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠DAE=∠BEA,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠BEA=∠BAE,
∴AB=BE,
∴BE=CD.
(2)解:如图2,连接BG,CG,
∵四边形ABCD是平行四边形,∠ABC=90°,
∴四边形ABCD是矩形,
∴∠BCD=∠ADC=∠BAD=90°,
∴∠ECF=90°,∠DAE=∠BAE=∠BAD=45°,
∴∠F=∠DAF=45°,
∴∠CEF=∠F=45°,
∴FD=AD=CB,FC=EC,
∵G是EF的中点,
∴CG⊥EF,CG=FG=EG=EF,∠BCG=∠FCG=∠ECF=45°,
∴∠F=∠BCG,
在△DFG和△BCG中,
,
∴△DFG≌△BCG(SAS),
∴DG=BG,∠DGF=∠BGC,
∵∠CGF=∠CGE=90°,
∴∠BGD=∠BGC-∠CGE+∠DGE=∠DGF-∠CGF+∠DGE=∠CGE=90°,
∴∠BDG=∠DBG=45°,
∴∠BDG的度数是45°.
27.【答案】(0,2),(4,2);
D(1,4);
.
28.【答案】17;
;
.
第1页,共1页
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列图形既是中心对称图形,也是轴对称图形的是( )
A. B. C. D.
2.下列计算正确的是( )
A. B. C. D.
3.下列二次根式与是同类二次根式的是( )
A. B. C. D.
4.矩形具备但是平行四边形不一定具备的性质是( )
A. 两组对边分别相等 B. 两组对角分别相等
C. 两条对角线相等 D. 两条对角线互相平分
5.已知ab<0,且,,则a+b结果是( )
A. 8 B. 2 C. -2 D. -8
6.如图 ABCD,E,F分别是边AD,BC上的点,且AE=BF,连接AF与BE相交于点P,连接DF与CE相交于点Q,若S△ABP=3,S ABCD=36,则阴影部分的面积为( )
A. 15 B. 16 C. 17 D. 18
7.如图,将△ABC绕点A逆时针旋转60°得到△ADE,DE与BC交于点P,下列结论:①BC=DE;②PA平分∠BPE;③PA+PC=PE;④PA+PD=PB.其中正确的有( )
A. 1个
B. 2个
C. 3个
D. 4个
8.如图,在Rt△ABC中,∠BAC=90°,∠B=60°,AB=4,P为BC边上的动点,以PA,PC为邻边作 PAQC,连接PQ,则PQ长的最小值是( )
A. 2 B. 4 C. D.
二、填空题:本题共10小题,每小题3分,共30分。
9.函数的定义域是______.
10.比较大小: ______.(填“>”、“<”或“=”)
11.二次根式,,,,中是最简二次根式的是______.
12.已知,则= ______.
13.实数a,b在数轴上的位置如图所示,则化简的值是______.
14.对于任意两个不相等的正实数a,b,定义一种新运算“ ”,即,如,则6 8= ______.
15.如图,将矩形ABCD绕点A顺时针旋转到矩形AEFG的位置,已知∠1=110°,则旋转角α= ______.
16.如图矩形ABCD,点E在BC的延长线上,CE=BD,连接AE,如果∠E=28°,则∠ADB= ______.
17.如图 ABCD,∠ABC=135°,E在CD的延长线上,F在BC上,AE∥BD,EF⊥BC,已知EF=4,则AB的长是______.
18.整数x满足0<x<60,且二次根式与是同类二次根式,则x= ______.
三、解答题:本题共10小题,共96分。解答应写出文字说明,证明过程或演算步骤。
19.(本小题8分)
计算:
(1)×;
(2).
20.(本小题8分)
化简:
(1);
(2).
21.(本小题8分)
(1)已知x、y为实数,且,求的值;
(2)已知x+y=7,xy=8,求代数式x2+y2的值.
22.(本小题8分)
如图直角坐标系,网格中最小正方形的边长为1,已知△ABC.
(1)画出△ABC关于原点成中心对称的△A1B1C1;
(2)画出将△ABC绕坐标原点O逆时针旋转90°,得到△A2B2C2;
(3)请直接写出以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
23.(本小题10分)
如图,在△ABC中(∠BAC≠60°),在BC的同侧作正△ABF、正△ACD和正△BCE.
(1)求证:四边形ADEF是平行四边形;
(2)当∠BAC= ______时,四边形ADEF是矩形.
24.(本小题10分)
如图矩形ABCD,作BE⊥AC,DF⊥AC,垂足分别是E,F.
(1)求证:四边形DEBF是平行四边形;
(2)若AB=2,AC=4,求四边形DEBF的面积.
25.(本小题10分)
根据所给的方法,完成下列问题:
分母有理化:.
解:.
(1)计算:;
(2)已知,,求x2+y2的值.
26.(本小题10分)
在 ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明BE=CD;
(2)在图2中,若∠ABC=90°,G是EF的中点,求∠BDG的度数.
27.(本小题12分)
如图①,在平面直角坐标系中,已知 ABCD在第一象限,点A在y的正半轴,AB∥x轴.直线y=-x从原点出发沿x轴正方向向右平移,在平移过程中直线y=-x被 ABCD截得的线段长度l与直线在x轴上平移的距离m的函数图象如图②所示.
(1)直接写出点A,B的坐标:A ______,B ______;
(2)求点D的坐标;
(3)当直线y=-x平分 ABCD的面积时,m= ______.
28.(本小题12分)
如图正方形网格中最小正方形的边长都是1,每个小正方形的顶点称为格点, ABCD的顶点A、B、C、D都在格点上,只用无刻度的直尺,分别在给定的网格中按下列要求作图,保留作图痕迹.
(1) ABCD的面积为______;
(2)在图①中,画出 ABCD的边AD上的高BE,并求BE的长;
(3)在图②中,在 ABCD的边AD上找一点F,连结AF,使∠ABF=45°,并直接写出BF的长:______.
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】C
5.【答案】B
6.【答案】A
7.【答案】D
8.【答案】C
9.【答案】x>-2
10.【答案】<
11.【答案】
12.【答案】2
13.【答案】b
14.【答案】
15.【答案】20°
16.【答案】56°
17.【答案】2
18.【答案】3或23
19.【答案】3+2;
2-.
20.【答案】3;
m.
21.【答案】2;
14.
22.【答案】如图,△A1B1C1即为所求;
如图,△A2B2C2即为所求;
、
如图,D1(-4,5),D2(2,3),D3(-4,-1).
23.【答案】证明:∵△ABF、△ACD、△BCE都是正三角形,
∴AB=BF=AF,AC=CD=AD,BE=BC=CE,∠ABF=∠CBE=∠BCE=∠ACD=60°,
∴∠ABF-∠ABE=∠CBE-∠ABE,
即∠FBE=∠ABC,
在△FBE和△ABC中,
,
∴△FBE≌△ABC(SAS),
∴EF=AC,
同理:△DEC≌△ABC(SAS),
∴DE=AB,
∴DE=AB=AF,EF=AC=AD,
∴四边形ADEF是平行四边形;
150°.
24.【答案】证明:∵四边形ABCD是矩形,
∴AB∥CD,AB=CD,
∴∠BAE=∠DCF,
∵BE⊥AC,DF⊥AC,
∴BE∥DF,∠AEB=∠CFD=90°,
∴△AEB≌△CFD(AAS),
∴BE=DF,
∴四边形DEBF是平行四边形;
2.
25.【答案】9;
1.
26.【答案】(1)证明:如图1,∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠DAE=∠BEA,
∵AE平分∠BAD,
∴∠DAE=∠BAE,
∴∠BEA=∠BAE,
∴AB=BE,
∴BE=CD.
(2)解:如图2,连接BG,CG,
∵四边形ABCD是平行四边形,∠ABC=90°,
∴四边形ABCD是矩形,
∴∠BCD=∠ADC=∠BAD=90°,
∴∠ECF=90°,∠DAE=∠BAE=∠BAD=45°,
∴∠F=∠DAF=45°,
∴∠CEF=∠F=45°,
∴FD=AD=CB,FC=EC,
∵G是EF的中点,
∴CG⊥EF,CG=FG=EG=EF,∠BCG=∠FCG=∠ECF=45°,
∴∠F=∠BCG,
在△DFG和△BCG中,
,
∴△DFG≌△BCG(SAS),
∴DG=BG,∠DGF=∠BGC,
∵∠CGF=∠CGE=90°,
∴∠BGD=∠BGC-∠CGE+∠DGE=∠DGF-∠CGF+∠DGE=∠CGE=90°,
∴∠BDG=∠DBG=45°,
∴∠BDG的度数是45°.
27.【答案】(0,2),(4,2);
D(1,4);
.
28.【答案】17;
;
.
第1页,共1页
同课章节目录
