2024-2025学年江苏省泰州市靖江市滨江学校七年级(下)第二次联考数学试卷(5月份)(含部分答案)
文档属性
| 名称 | 2024-2025学年江苏省泰州市靖江市滨江学校七年级(下)第二次联考数学试卷(5月份)(含部分答案) |  | |
| 格式 | docx | ||
| 文件大小 | 162.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 19:56:32 | ||
图片预览



文档简介
2024-2025学年江苏省泰州市靖江市滨江学校七年级(下)第二次联考数学试卷(5月份)
一、选择题:本题共6小题,每小题3分,共18分。在每小题给出的选项中,只有一项是符合题目要求的。
1.志愿服务,传递爱心,传递文明,下列志愿服务标志为轴对称图形的是( )
A. B. C. D.
2.下列句子中,是真命题的是( )
A. 你的作业做完了吗? B. 相等的角是对顶角
C. 过直线l外一点作l的平行线 D. 负数都小于0
3.若a>b,则下列不等式成立的是( )
A. a+2<b+2 B. a-2>b-2 C. 2a<2b D. -2a>-2b
4.下列说法错误的是( )
A. 图形的平移后,每组对应点之间的距离相等
B. 图形的旋转后,对应点到旋转中心的距离相等
C. 两个图形关于某条直线对称,对应点一定在直线的两旁
D. 两个图形如果关于一条直线成轴对称,那么由这两个图形所组成的图形是轴对称图形
5.《九章算术》是中国古代数学专著,该书内容十分丰富,系统总结了战国、秦、汉时期的数学成就.其中第八章“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,现在我们把它改为横排,如图1、图2.图中,各行从左到右列出的算筹数,分别表示未知数x、y的系数与相应的常数项.把图1所示的算筹图,用我们现在所熟悉的方程组形式表述出来就是,类似地,图2所示的算筹图,我们可以表述为( )
A. B. C. D.
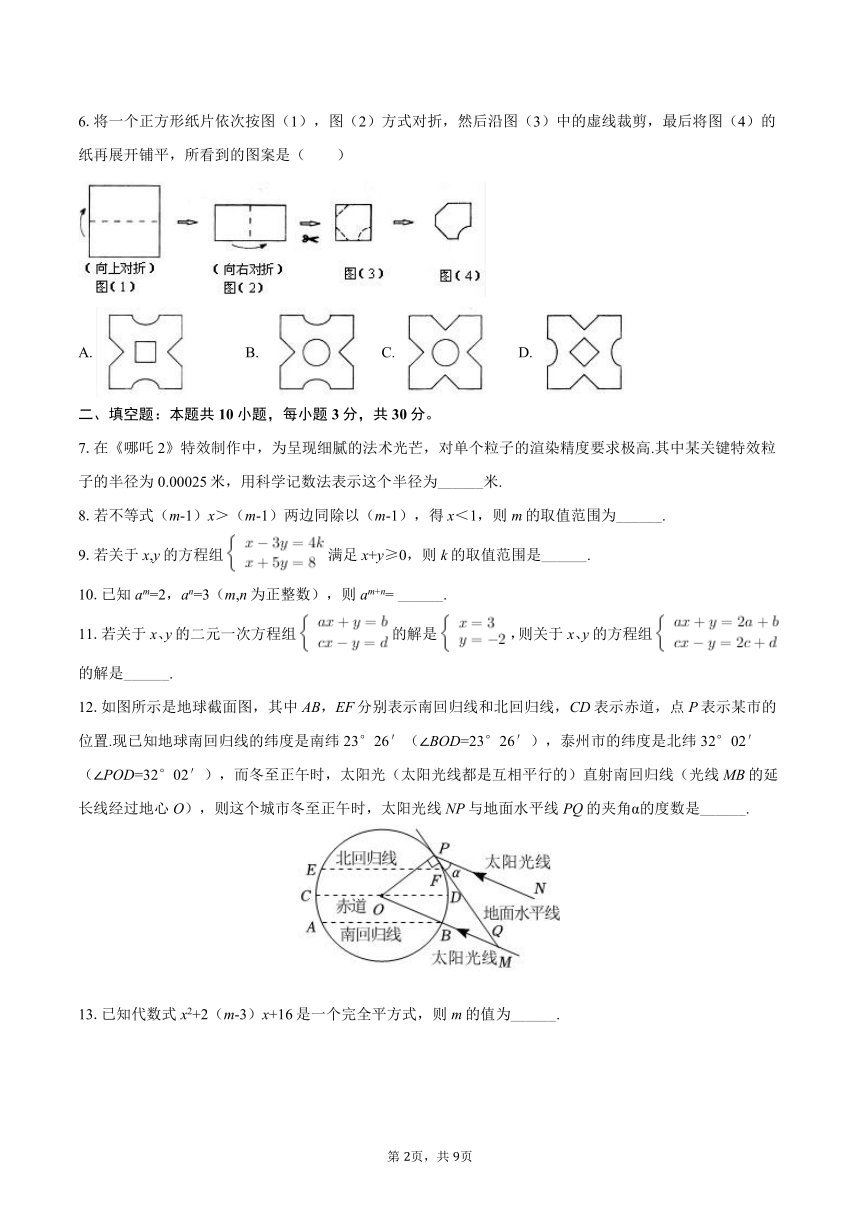
6.将一个正方形纸片依次按图(1),图(2)方式对折,然后沿图(3)中的虚线裁剪,最后将图(4)的纸再展开铺平,所看到的图案是( )
A. B. C. D.
二、填空题:本题共10小题,每小题3分,共30分。
7.在《哪吒2》特效制作中,为呈现细腻的法术光芒,对单个粒子的渲染精度要求极高.其中某关键特效粒子的半径为0.00025米,用科学记数法表示这个半径为______米.
8.若不等式(m-1)x>(m-1)两边同除以(m-1),得x<1,则m的取值范围为______.
9.若关于x,y的方程组满足x+y≥0,则k的取值范围是______.
10.已知am=2,an=3(m,n为正整数),则am+n= ______.
11.若关于x、y的二元一次方程组的解是,则关于x、y的方程组的解是______.
12.如图所示是地球截面图,其中AB,EF分别表示南回归线和北回归线,CD表示赤道,点P表示某市的位置.现已知地球南回归线的纬度是南纬23°26′(∠BOD=23°26′),泰州市的纬度是北纬32°02′(∠POD=32°02′),而冬至正午时,太阳光(太阳光线都是互相平行的)直射南回归线(光线MB的延长线经过地心O),则这个城市冬至正午时,太阳光线NP与地面水平线PQ的夹角α的度数是______.
13.已知代数式x2+2(m-3)x+16是一个完全平方式,则m的值为______.
14.某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到敬老院慰问老人.如果分给每位老人4盒牛奶,那么剩下28盒牛奶;如果分给每位老人5盒牛奶,那么最后一位老人分得的牛奶不足4盒,但至少1盒.则这个敬老院的老人最少有______.
15.不等式2x+1>m+3有2个负整数解,则m的取值范围______.
16.已知a,b,c满足a2+2b=7,b2-2c=-1,c2-6a=-17,则a+2b-3c的值为______.
三、解答题:本题共10小题,共102分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题12分)
计算:
(1);
(2)(-a)3 a2+(2a4)2÷a3;
(3)(x+1)2-x(x-1);
(4)(x-2y)2-(3x+y)(3x-y).
18.(本小题9分)
(1)用乘法公式计算:1232-124×122;
(2)先化简,再求值:(3a+b)2-(3a+b)(3a-b)-2b2,其中a=,b=-2.
19.(本小题10分)
解方程组或不等式组:
(1);
(2).
20.(本小题9分)
如图,在一个10×10的正方形网格中有一个△ABC,△ABC的顶点都在格点上.
(1)在网格中画出△ABC向下平移4个单位,再向右平移6个单位得到的△A1B1C1;
(2)在网格中画出△ABC关于点P成中心对称得到的△A2B2C2;
(3)若可将△A1B1C1绕点O旋转得到△A2B2C2,请在正方形网格中标出点O.
21.(本小题6分)
奥运会过后掀起一股滑雪的热潮,很多同学纷纷来到滑雪场,想亲身感受一下奥运健儿在赛场上风驰电掣的感觉,但是第一次走进滑雪场的你,学会正确的滑雪姿势是最重要的,正确的滑雪姿势是上身挺直略前倾,与小腿平行,使脚的根部处于微微受力的状态,如图所示,AB∥CD,如果人的小腿CD与地面的夹角∠CDE=60°,求出身体BA与水平线的夹角∠BAF的度数.
22.(本小题10分)
如图,在六边形ABCDEF中,AF∥BE∥CD,ED∥AB,∠A=110°,∠ABC=100°.
(1)求六边形ABCDEF内角和的度数;
(2)求∠C、∠D的度数;
(3)若一只蚂蚁从AB的中点出发沿A-B-C-D-E-F-A的方向运动到AB的中点停止,蚂蚁一共转过了多少度?
23.(本小题10分)
如果一个正整数能表示为两个连续偶数的平方差,那么我们称这个正整数为“靖兴数”,如4=22-02,12=42-22,20=62-42,因此,4,12,20这三个数都是“靖兴数”.
(1)m、n为连续偶数(m>n),当28=m2-n2时,m+n= ______;
(2)设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连续偶数构成的“靖兴数”是4的倍数吗?为什么?
24.(本小题10分)
某中学为落实《教育部办公厅关于进一步加强中小学生体质管理的通知》文件要求,决定增设篮球、足球两门选修课程,需要购进一批篮球和足球.已知购买2个篮球和3个足球共需费用510元;购买3个篮球和5个足球共需费用810元.
(1)求篮球和足球的单价分别是多少元;
(2)学校计划采购篮球、足球共50个,并要求篮球不少于30个,且总费用不超过5500元.那么有哪几种购买方案?
25.(本小题12分)
我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.
例如图1可以得到(a+b)2=a2+2ab+b2,基于此,请解答下列问题:
(1)根据图2,写出一个代数恒等式:______.
(2)利用(1)中得到的结论,解决下面的问题:
①若a+b+c=10,ab+ac+bc=36,求a2+b2+c2的值;
②若三个实数x,y,z满足2x×4y÷8z=16,x2+4y2+9z2=56,求2xy-3xz-6yz的值.
26.(本小题14分)
已知AB∥CD,M、N分别在AB、CD上.
(1)如图(1),已知∠AME=15°,∠CNE=45°,求出∠MEN的大小;
(2)如图(2),∠AME的平分线所在直线与∠DNE的平分线相交于点Q,∠MEN=70°.根据题意,在图中补全图形,并求∠MQN的度数;
(3)如图(3),连接MN,∠AMN=100°,射线ME从MA开始,绕M点以10°每秒的速度逆时针旋转,同时射线NF从ND开始,绕N点以20°每秒的速度逆时针旋转,直线ME与射线NF交于P,若△MNP中有两个角相等,直接写出运动时间t秒(0≤t≤9)的值______.
1.【答案】D
2.【答案】D
3.【答案】B
4.【答案】C
5.【答案】D
6.【答案】D
7.【答案】2.5×10-4
8.【答案】m<1.
9.【答案】k≥-2
10.【答案】6
11.【答案】
12.【答案】34°32′
13.【答案】7或-1
14.【答案】30
15.【答案】-8≤m<-6
16.【答案】-2
17.【答案】4; 3 a5; 3 x+1; -8 x2-4xy+5y2.
18.【答案】1;
6 ab,原式=4.
19.【答案】;
x>3.
20.【答案】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)如图,连接A1A2,B1B2,C1C2,相交于点O,
则△A1B1C1绕点O旋转180°得到△A2B2C2,
则点O即为所求.
21.【答案】∠BAF=60°.
22.【答案】720°; ∠ C=150°,∠D=110°; 360°.
23.【答案】14;
这两个连续偶数构成的“靖兴数”是4的倍数,理由见解析.
24.【答案】解:(1)设篮球的单价为a元,足球的单价为b元,
由题意可得:,
解得,
答:篮球的单价为120元,足球的单价为90元;
(2)设采购篮球x个,则采购足球为(50-x)个,
∵要求篮球不少于30个,且总费用不超过5500元,
∴,
解得30≤x≤33,
∵x为整数,
∴x的值可为30,31,32,33,
∴共有四种购买方案,
方案一:采购篮球30个,采购足球20个;
方案二:采购篮球31个,采购足球19个;
方案三:采购篮球32个,采购足球18个;
方案四:采购篮球33个,采购足球17个.
25.【答案】(a+b+c)2=a2+b2+c2+2ab+2bc+2ac; ①28;②-20.
26.【答案】60°;
55°;
.
第1页,共1页
一、选择题:本题共6小题,每小题3分,共18分。在每小题给出的选项中,只有一项是符合题目要求的。
1.志愿服务,传递爱心,传递文明,下列志愿服务标志为轴对称图形的是( )
A. B. C. D.
2.下列句子中,是真命题的是( )
A. 你的作业做完了吗? B. 相等的角是对顶角
C. 过直线l外一点作l的平行线 D. 负数都小于0
3.若a>b,则下列不等式成立的是( )
A. a+2<b+2 B. a-2>b-2 C. 2a<2b D. -2a>-2b
4.下列说法错误的是( )
A. 图形的平移后,每组对应点之间的距离相等
B. 图形的旋转后,对应点到旋转中心的距离相等
C. 两个图形关于某条直线对称,对应点一定在直线的两旁
D. 两个图形如果关于一条直线成轴对称,那么由这两个图形所组成的图形是轴对称图形
5.《九章算术》是中国古代数学专著,该书内容十分丰富,系统总结了战国、秦、汉时期的数学成就.其中第八章“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,现在我们把它改为横排,如图1、图2.图中,各行从左到右列出的算筹数,分别表示未知数x、y的系数与相应的常数项.把图1所示的算筹图,用我们现在所熟悉的方程组形式表述出来就是,类似地,图2所示的算筹图,我们可以表述为( )
A. B. C. D.
6.将一个正方形纸片依次按图(1),图(2)方式对折,然后沿图(3)中的虚线裁剪,最后将图(4)的纸再展开铺平,所看到的图案是( )
A. B. C. D.
二、填空题:本题共10小题,每小题3分,共30分。
7.在《哪吒2》特效制作中,为呈现细腻的法术光芒,对单个粒子的渲染精度要求极高.其中某关键特效粒子的半径为0.00025米,用科学记数法表示这个半径为______米.
8.若不等式(m-1)x>(m-1)两边同除以(m-1),得x<1,则m的取值范围为______.
9.若关于x,y的方程组满足x+y≥0,则k的取值范围是______.
10.已知am=2,an=3(m,n为正整数),则am+n= ______.
11.若关于x、y的二元一次方程组的解是,则关于x、y的方程组的解是______.
12.如图所示是地球截面图,其中AB,EF分别表示南回归线和北回归线,CD表示赤道,点P表示某市的位置.现已知地球南回归线的纬度是南纬23°26′(∠BOD=23°26′),泰州市的纬度是北纬32°02′(∠POD=32°02′),而冬至正午时,太阳光(太阳光线都是互相平行的)直射南回归线(光线MB的延长线经过地心O),则这个城市冬至正午时,太阳光线NP与地面水平线PQ的夹角α的度数是______.
13.已知代数式x2+2(m-3)x+16是一个完全平方式,则m的值为______.
14.某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到敬老院慰问老人.如果分给每位老人4盒牛奶,那么剩下28盒牛奶;如果分给每位老人5盒牛奶,那么最后一位老人分得的牛奶不足4盒,但至少1盒.则这个敬老院的老人最少有______.
15.不等式2x+1>m+3有2个负整数解,则m的取值范围______.
16.已知a,b,c满足a2+2b=7,b2-2c=-1,c2-6a=-17,则a+2b-3c的值为______.
三、解答题:本题共10小题,共102分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题12分)
计算:
(1);
(2)(-a)3 a2+(2a4)2÷a3;
(3)(x+1)2-x(x-1);
(4)(x-2y)2-(3x+y)(3x-y).
18.(本小题9分)
(1)用乘法公式计算:1232-124×122;
(2)先化简,再求值:(3a+b)2-(3a+b)(3a-b)-2b2,其中a=,b=-2.
19.(本小题10分)
解方程组或不等式组:
(1);
(2).
20.(本小题9分)
如图,在一个10×10的正方形网格中有一个△ABC,△ABC的顶点都在格点上.
(1)在网格中画出△ABC向下平移4个单位,再向右平移6个单位得到的△A1B1C1;
(2)在网格中画出△ABC关于点P成中心对称得到的△A2B2C2;
(3)若可将△A1B1C1绕点O旋转得到△A2B2C2,请在正方形网格中标出点O.
21.(本小题6分)
奥运会过后掀起一股滑雪的热潮,很多同学纷纷来到滑雪场,想亲身感受一下奥运健儿在赛场上风驰电掣的感觉,但是第一次走进滑雪场的你,学会正确的滑雪姿势是最重要的,正确的滑雪姿势是上身挺直略前倾,与小腿平行,使脚的根部处于微微受力的状态,如图所示,AB∥CD,如果人的小腿CD与地面的夹角∠CDE=60°,求出身体BA与水平线的夹角∠BAF的度数.
22.(本小题10分)
如图,在六边形ABCDEF中,AF∥BE∥CD,ED∥AB,∠A=110°,∠ABC=100°.
(1)求六边形ABCDEF内角和的度数;
(2)求∠C、∠D的度数;
(3)若一只蚂蚁从AB的中点出发沿A-B-C-D-E-F-A的方向运动到AB的中点停止,蚂蚁一共转过了多少度?
23.(本小题10分)
如果一个正整数能表示为两个连续偶数的平方差,那么我们称这个正整数为“靖兴数”,如4=22-02,12=42-22,20=62-42,因此,4,12,20这三个数都是“靖兴数”.
(1)m、n为连续偶数(m>n),当28=m2-n2时,m+n= ______;
(2)设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连续偶数构成的“靖兴数”是4的倍数吗?为什么?
24.(本小题10分)
某中学为落实《教育部办公厅关于进一步加强中小学生体质管理的通知》文件要求,决定增设篮球、足球两门选修课程,需要购进一批篮球和足球.已知购买2个篮球和3个足球共需费用510元;购买3个篮球和5个足球共需费用810元.
(1)求篮球和足球的单价分别是多少元;
(2)学校计划采购篮球、足球共50个,并要求篮球不少于30个,且总费用不超过5500元.那么有哪几种购买方案?
25.(本小题12分)
我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.
例如图1可以得到(a+b)2=a2+2ab+b2,基于此,请解答下列问题:
(1)根据图2,写出一个代数恒等式:______.
(2)利用(1)中得到的结论,解决下面的问题:
①若a+b+c=10,ab+ac+bc=36,求a2+b2+c2的值;
②若三个实数x,y,z满足2x×4y÷8z=16,x2+4y2+9z2=56,求2xy-3xz-6yz的值.
26.(本小题14分)
已知AB∥CD,M、N分别在AB、CD上.
(1)如图(1),已知∠AME=15°,∠CNE=45°,求出∠MEN的大小;
(2)如图(2),∠AME的平分线所在直线与∠DNE的平分线相交于点Q,∠MEN=70°.根据题意,在图中补全图形,并求∠MQN的度数;
(3)如图(3),连接MN,∠AMN=100°,射线ME从MA开始,绕M点以10°每秒的速度逆时针旋转,同时射线NF从ND开始,绕N点以20°每秒的速度逆时针旋转,直线ME与射线NF交于P,若△MNP中有两个角相等,直接写出运动时间t秒(0≤t≤9)的值______.
1.【答案】D
2.【答案】D
3.【答案】B
4.【答案】C
5.【答案】D
6.【答案】D
7.【答案】2.5×10-4
8.【答案】m<1.
9.【答案】k≥-2
10.【答案】6
11.【答案】
12.【答案】34°32′
13.【答案】7或-1
14.【答案】30
15.【答案】-8≤m<-6
16.【答案】-2
17.【答案】4; 3 a5; 3 x+1; -8 x2-4xy+5y2.
18.【答案】1;
6 ab,原式=4.
19.【答案】;
x>3.
20.【答案】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)如图,连接A1A2,B1B2,C1C2,相交于点O,
则△A1B1C1绕点O旋转180°得到△A2B2C2,
则点O即为所求.
21.【答案】∠BAF=60°.
22.【答案】720°; ∠ C=150°,∠D=110°; 360°.
23.【答案】14;
这两个连续偶数构成的“靖兴数”是4的倍数,理由见解析.
24.【答案】解:(1)设篮球的单价为a元,足球的单价为b元,
由题意可得:,
解得,
答:篮球的单价为120元,足球的单价为90元;
(2)设采购篮球x个,则采购足球为(50-x)个,
∵要求篮球不少于30个,且总费用不超过5500元,
∴,
解得30≤x≤33,
∵x为整数,
∴x的值可为30,31,32,33,
∴共有四种购买方案,
方案一:采购篮球30个,采购足球20个;
方案二:采购篮球31个,采购足球19个;
方案三:采购篮球32个,采购足球18个;
方案四:采购篮球33个,采购足球17个.
25.【答案】(a+b+c)2=a2+b2+c2+2ab+2bc+2ac; ①28;②-20.
26.【答案】60°;
55°;
.
第1页,共1页
同课章节目录
