河北省邯郸市育华中学2025年九年级下学期中考四模数学试卷(含答案)
文档属性
| 名称 | 河北省邯郸市育华中学2025年九年级下学期中考四模数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 371.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 21:08:04 | ||
图片预览



文档简介
2025年河北省邯郸市丛台区育华中学中考数学四模试卷
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.表示代数式“”的意义正确的是( )
A. B. C. D.
2.在如图所示的平面内,点P是直线l外一点,过点P可作a条直线l的垂线,过点P可作b条直线l的平行线,则的值为( )
A. 0 B. 1 C. 2 D. 无法确定
3.关于x的不等式的解集如图所示,则m的值是( )
A. 3 B. C. 2 D.
4.如图,与是位似图形,则位似中心可以是( )
A. 点M B. 点N C. 点Q D. 点P
5.某市准备规划一座长为,宽为的矩形市民健身娱乐场所,则该场所的面积用科学记数法表示为( )
A. B. C. D.
6.如图是嘉嘉用6块相同的小正方体搭成的几何体,若淇淇拿走其中的n个小正方体后,发现该几何体的左视图没有发生变化,则n的最大值为( )
A. 1 B. 2 C. 3 D. 4
7.若,则代数式的值是( )
A. B. 2 C. D. 4
8.如图,四边形ABCD内接于,点I是的内心,,点E在AD的延长线上,则的度数为
A. B. C. D.
9.“行人守法,安全过街”体现了对生命的尊重,也体现了公民的文明素质,更反映了城市的文明程度.在某路口的斑马线路段横穿双向车道,其中,米,在人行绿灯亮时,小刚共用时10秒通过AC,其中通过BC的速度是通过AB的倍,求小刚通过AB的速度.设小刚通过AB的速度为x米/秒,则根据题意列方程为( )
A. B. C. D.
10.关于x的一元二次方程的根的情况,下列说法正确的是( )
A. 实数根的个数由b的值确定 B. 没有实数根
C. 两根互为倒数 D. 若,则两根互为相反数
11.如图,点P在正六边形ABCDEF的对角线BE上移动,以点A为圆心、线段AP的长为半径作弧,交射线AF于点若,则AQ的长可以是( )
A.
B. 3cm
C.
D. 7cm
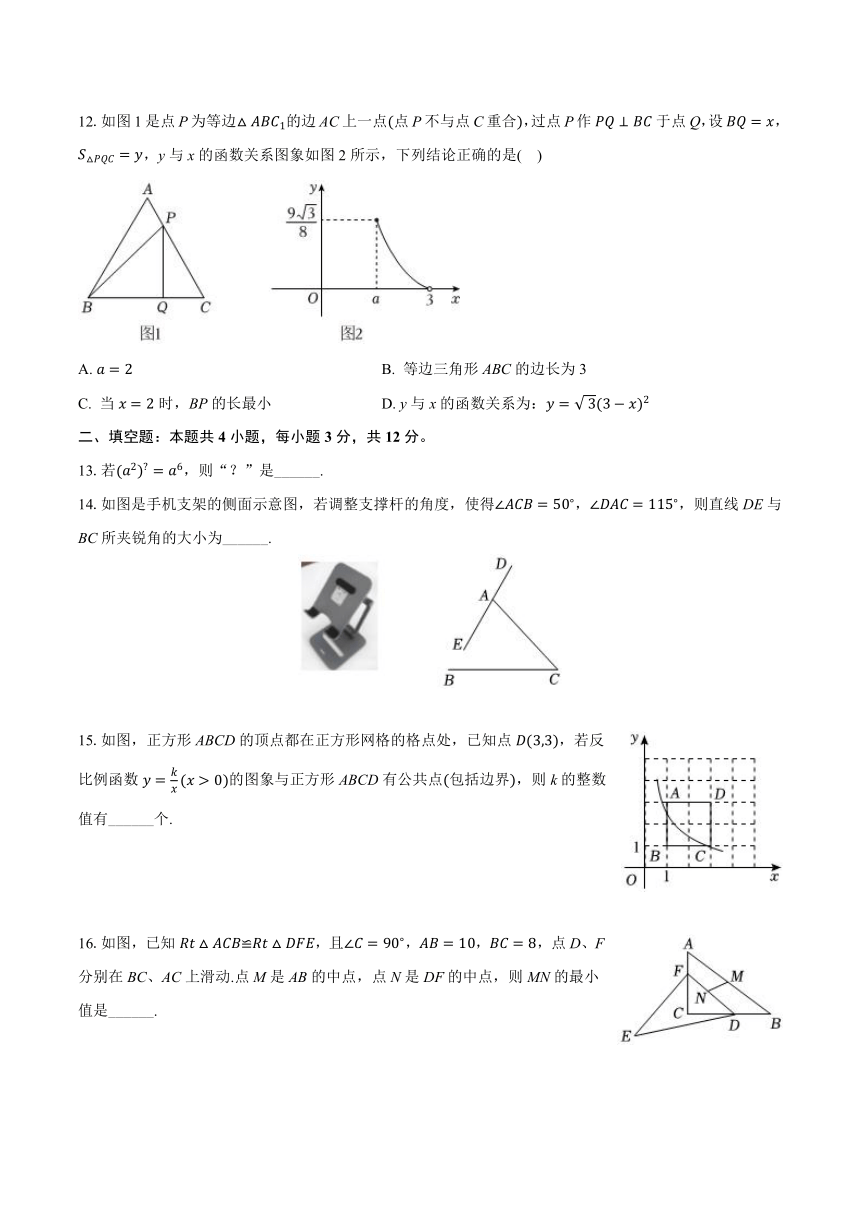
12.如图1是点P为等边的边AC上一点点P不与点C重合,过点P作于点Q,设,,y与x的函数关系图象如图2所示,下列结论正确的是( )
A. B. 等边三角形ABC的边长为3
C. 当时,BP的长最小 D. y与x的函数关系为:
二、填空题:本题共4小题,每小题3分,共12分。
13.若,则“?”是______.
14.如图是手机支架的侧面示意图,若调整支撑杆的角度,使得,,则直线DE与BC所夹锐角的大小为______.
15.如图,正方形ABCD的顶点都在正方形网格的格点处,已知点,若反比例函数的图象与正方形ABCD有公共点包括边界,则k的整数值有______个.
16.如图,已知,且,,,点D、F分别在BC、AC上滑动.点M是AB的中点,点N是DF的中点,则MN的最小值是______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题7分
如图,容器中装有5个小球,小球上分别标有数字:,0,5,2,现从容器中随机摸出四个小球,对小球上的数字进行运算.
①若摸出的四个小球上分别标有2,,0,,计算:;
②若摸出的四个数字的积不为0,求这四个数字的和;
将摸出的四个小球上的数字按一定顺序填入“□-□-□-□”中的“□”内,计算所得算式的结果,直接写出计算结果的最小值.
18.本小题8分
下面是一道例题及其解答过程的一部分,其中A、B是关于n的多项式.
例:先去括号,再合并同类项:
解:
=…
①直接写出:______,______;
②直接写出:原式的运算结果为______;
若n为任意正整数,试说明的值总能被7整除.
19.本小题9分
为提高在校生消防安全意识,现从某校抽取一部分学生进行消防安全知识检测,男生女生分开进行,将男生成绩绘制成条形统计图其中得4分的人数丢失,女生成绩绘制成扇形统计图,若从参赛的男生中随机抽取一人,抽到得4分的概率为
计算男生得4分的人数,补全条形统计图;
若男生的人数是女生的人数的2倍,男生成绩中位数是a,女生成绩众数是b,求的值;
若扇形图中的和是邻补角,求女生得分为5分的扇形的圆心角度数,并比较此时男生和女生平均成绩的大小.
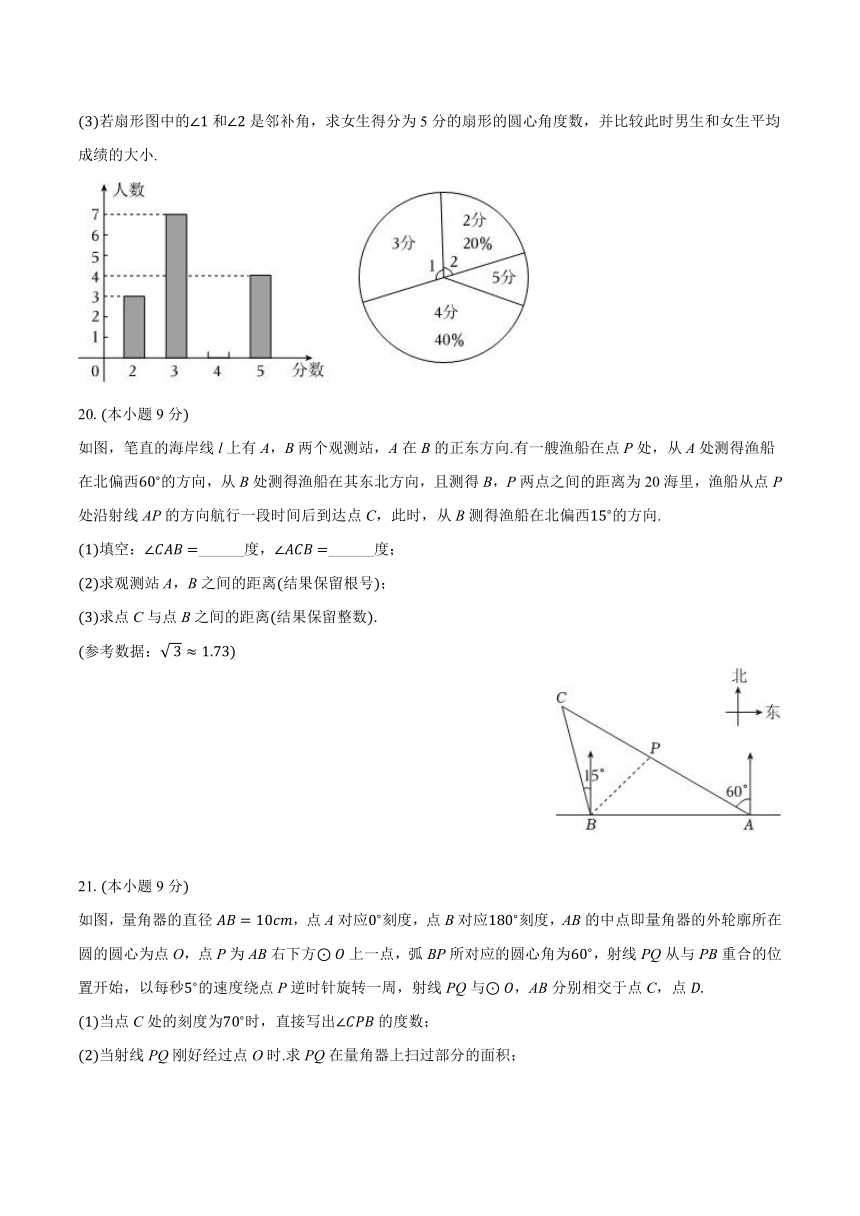
20.本小题9分
如图,笔直的海岸线l上有A,B两个观测站,A在B的正东方向.有一艘渔船在点P处,从A处测得渔船在北偏西的方向,从B处测得渔船在其东北方向,且测得B,P两点之间的距离为20海里,渔船从点P处沿射线AP的方向航行一段时间后到达点C,此时,从B测得渔船在北偏西的方向.
填空:______度,______度;
求观测站A,B之间的距离结果保留根号;
求点C与点B之间的距离结果保留整数
参考数据:
21.本小题9分
如图,量角器的直径,点A对应刻度,点B对应刻度,AB的中点即量角器的外轮廓所在圆的圆心为点O,点P为AB右下方上一点,弧BP所对应的圆心角为,射线PQ从与PB重合的位置开始,以每秒的速度绕点P逆时针旋转一周,射线PQ与,AB分别相交于点C,点
当点C处的刻度为时,直接写出的度数;
当射线PQ刚好经过点O时.求PQ在量角器上扫过部分的面积;
当射线PQ旋转至与相切时,求射线PQ旋转的时间.
22.本小题9分
如图,已知一次函数的图象经过点,
求这个一次函数;
若点在该函数图象上,连接OC,求的面积;
若点是该函数图象上的一个动点,点D坐标为连接DP,将线段DP绕点D顺时针旋转得到线段DQ,点Q是否能落在第三象限,若能,请直接写出m的取值范围;若不能,请说明理由.
23.本小题10分
消防员正在对一处着火点A进行喷水灭火,水流路线L为抛物线的一部分.建立如图所示的平面直角坐标系,已知消防车上的喷水口B高出地面2m,距离原点的水平距离为6m,着火点A距离点B的水平距离为10m,且点B,A分别位于y轴左右两侧,抛物线L的解析式为其中b,c为常数
写出点B的坐标,并用含b的代数式表示c;
若着火点A高出地面
①求水流恰好经过着火点A时抛物线L的解析式,并求它的对称轴;
②为彻底消除隐患,消防员对距着火点A水平距离1m的范围内继续进行喷水,直接写出抛物线水流路线解析式中b的取值范围包含端点是______,及c的最小值是______.
24.本小题11分
如图1,在平行四边形ABCD中,于点E,且点P从点E出发,沿向终点C运动,设点P在该折线上运动的路径长为,连接
的长为______,当点 P在BC上运动时,EP的最小值为______;
点F是AE的中点,如图2,
①请用无刻度的直尺和圆规过点F作BC的垂线FG,垂足为点保留作图痕迹,不写作法;
②求证:≌;
延长PE到点M,使得,以CE,ME为邻边作平行四边形
①当点P在BC上,平行四边形CEMN对角线EN所在的直线恰好经过点D时,如图3,求x的值;
②当点A落在平行四边形CEMN的边上或内部时,直接写出x的取值范围.
答案和解析
1.A
解:,
故选:
2.C
解:根据题意可知,过点P作直线l的垂线,过点P作直线l的平行线,,
将,代入,可得
故选:
3.A
解:,
,
由数轴可知,该不等式的解集为,
,
解得,
故选:
4.D
解:如图,根据位似中心是位似点连线的交点,可知点P为位似中心,
故选:
5.C
解:
故选:
6.C
解:拿走其中的n个小正方体后,发现该几何体的左视图没有发生变化,可以拿走最左侧的一个和最右侧的两个,则n的最大值为
故选:
7.D
解:原式
当时.原式
故选:
8.C
解:点I是的内心,
,,
,
,
又四边形ABCD内接于,
,
故选:
9.A
解:米,
米.
小刚通过AB的速度为x米/秒,通过BC的速度是通过AB的倍,
小刚通过BC的速度为米/秒.
又小刚共用时10秒通过AC,
故选:
10.D
解:,
此方程有两个不相等的实数根,
当时,方程变形为,解得或,即两根互为相反数,
故选:
11.C
解:如图,过点A作于点,
则由题意可知,,,
,
,,
在中,由勾股定理得,,
在中,由勾股定理得,,
当点P在正六边形ABCDEF的对角线BE上移动时,,
故选:
12.B
解:观察图象得:当时,,此时点P与点A重合,
由题意可得:此时点Q是BC的中点,
,,
此时,
此时,
解得:负值舍去,故A选项错误;
等边三角形ABC的边长为,故B选项正确;
在中,,,
,,
当时,取得最小值,BP长最小,故C选项错误;
,故D选项错误.
故选:
13.3
解:,
“?”是3,
故答案为:
根据幂的乘方法则计算即可.
本题考查了幂的乘方与积的乘方,熟练掌握运算法则是解题的关键.
14.
解:延长DE交BC于F,
,,
故答案为:
15.9
解:点,正方形ABCD的顶点都在正方形网格的格点处,
,
当反比例函数过点D时,,
当反比例函数过点B时,,
满足条件的k的取值范围为,其中共有9个k的整数值.
故答案为:
16.2
解:连接CN,CM,
,,,
,
,
,
点M是AB的中点,点N是DF的中点,,
,,
由三角形三边关系定理得到:,
的最小值是
故答案为:
17.①,②;
①
;
②摸出的四个数字的积不为0,
摸出的四个数字为,5,2,
;
根据有理数的加法法则可知,当摸出的四个小球上的数字为,0,5,2时,计算结果最小,
即
18.①;;②; 证明见解析.
①根据题意可知,,
则,
故答案为:;;
②
故答案为:;
原式
,
即n为任意正整数,的值总能被7整除.
19.6,图见解析;
;
,男生平均成绩>女生平均成绩.
设得4分的人数为x,则,解得,
经检验,是分式方程的解,
补全条形统计图如图,
男生人数为20人,
女生人数为10人,
由题意可知,男生成绩的第10,11个数分别为3和4,
中位数分,
观察扇形统计图可知 分,
;
若扇形图中的和是邻补角,则,即2分,3分所占的比例为,
分所占的比例为,
,
女生得分为5分的扇形的圆心角度数为,
男生平均成绩:分,
女生平均成绩:分,
男生平均成绩>女生平均成绩.
20.30,45;
观测站A,B之间的距离为海里;
点C与点B之间的距离约为27海里.
解:从A处测得点P处渔船在北偏西的方向,
,
从B处测得渔船点P处在其东北方向,从B测得点C渔船在北偏西的方向,
,
,
故答案为:30,45;
如图1,过点P作于D点,则,
在中,,海里,
海里,海里,
在中,,
海里,
海里,
观测站A,B之间的距离为海里;
根据题意,得如图2,过点P作于D点,过点B作,垂足为F,
在中,,,
海里.
在中,,,
海里,
则点C与点B之间的距离约为27海里.
21.; ; 当射线PQ旋转至与相切时,射线PQ旋转的时间为30秒或66秒.
解:的度数为
连接OC,如图,
点C处的刻度为,
,
,
;
连接PO并延长,交于点C,如图,
弧BP所对应的圆心角为,
,
,
在量角器上扫过部分为扇形
,
在量角器上扫过部分的面积为
连接PO,过点P作,如图,
,OP为的半径,
为的切线,
,,
为等边三角形,
,
,
情况一:当PQ旋转至位置时,
射线PQ旋转的角度为,
射线PQ从与PB重合的位置开始,以每秒的速度绕点P逆时针旋转,
射线PQ旋转的时间为秒
情况二:当PQ旋转至位置时,射线PQ转过的角度为,
射线PQ从与PB重合的位置开始,以每秒的速度绕点P逆时针旋转,
射线PQ旋转的时间为秒
综上所述,当射线PQ旋转至与相切时,射线PQ旋转的时间为30秒或66秒.
22.;
12;
点Q能落在第三象限;m的取值范围为;理由见解答过程.
解:已知一次函数的图象经过点,,将点A,点B的坐标分别代入得:
,
解得,
这个一次函数的解析式为;
点在图象上,将点C代入得:
,
解得,
,
的OB边上的高为,
又,
,
的面积为
点Q能落在第三象限;m的取值范围为;理由如下:
解:将点代入一次函数得:,
,
由题意,有以下两个临界位置:
①如图1,当轴时,将线段DP绕点D顺时针旋转得到线段DQ,点Q恰好落在y轴上,
点D坐标为,
此时,
解得;
②如图2,当将线段DP绕点D顺时针旋转得到线段DQ,点Q恰好落在x轴上时,
过点P作轴于点E,
,
点D坐标为,
,
轴,,
,
,
由旋转的性质得:,,
,
,
在和中,
,
≌,
,
,即,
将线段DP绕点D顺时针旋转得到线段DQ,点Q能落在第三象限,此时
23.点B的坐标为,;
①抛物线的解析式为:,对称轴为直线;②,
消防车上的喷水口B高出地面2m,距离原点的水平距离为6m,
点B的坐标为,
抛物线L的解析式为经过点,
,
整理得:;
①着火点A距离点B的水平距离为10m,着火点A高出地面3m,点B的坐标为,
,
,
由得,
抛物线的解析式为:,
水流恰好经过着火点A,
代入得:,
解得:,
,
抛物线的解析式为:,
对称轴为直线,
②消防员对距着火点A水平距离1m的范围内继续进行喷水,,
当抛物线经过点时,
,
解得:;
当抛物线经过点时,
,,
解得:,
综上可得:,
,,
随b的增大而增大,
当时,c取得最小值为,
的最小值为
故答案为:,
24.5;;
①见解析;
②见解析;
①;
②x的取值范围为;理由见解答过程.
解:在平行四边形ABCD中,于点E,且
,
,
解得:,
在直角三角形BCE中,由勾股定理得:,
当时,EP取得最小值,
,即,
解得:,
的最小值为;
故答案为:5;;
①如图2,即为所求;
②由作图知,
,即,
,
,
,
点F是AE的中点,
,
,
≌;
①点P从点E出发,沿向终点C运动,设点P在该折线上运动的路径长为,点P在BC上,平行四边形CEMN对角线EN所在的直线恰好经过点D时,如图3,
由题意得,,,,
,
,,
,
四边形 ABCD是平行四边形,
,,
,
,
,
,
,
,
∽,
,
,
,
,
解得;
②x的取值范围为;理由如下:
当P在BE上时,如图4,
,
,
当时,点A落在 CEMN的边上,
,
解得:,
;
当P在BC上时,如图5,过P作于Q,设MN与直线AB交于H,
,
,
,,,
,,
,
四边形CEMN是平行四边形,
,,
,
,
,
,
∽,
,
,
,
,,
当且时,点A落在 CEMN的边上或内部,
,
解得:,
,
综上所述,当时,点A落在 CEMN的边上或内部.
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.表示代数式“”的意义正确的是( )
A. B. C. D.
2.在如图所示的平面内,点P是直线l外一点,过点P可作a条直线l的垂线,过点P可作b条直线l的平行线,则的值为( )
A. 0 B. 1 C. 2 D. 无法确定
3.关于x的不等式的解集如图所示,则m的值是( )
A. 3 B. C. 2 D.
4.如图,与是位似图形,则位似中心可以是( )
A. 点M B. 点N C. 点Q D. 点P
5.某市准备规划一座长为,宽为的矩形市民健身娱乐场所,则该场所的面积用科学记数法表示为( )
A. B. C. D.
6.如图是嘉嘉用6块相同的小正方体搭成的几何体,若淇淇拿走其中的n个小正方体后,发现该几何体的左视图没有发生变化,则n的最大值为( )
A. 1 B. 2 C. 3 D. 4
7.若,则代数式的值是( )
A. B. 2 C. D. 4
8.如图,四边形ABCD内接于,点I是的内心,,点E在AD的延长线上,则的度数为
A. B. C. D.
9.“行人守法,安全过街”体现了对生命的尊重,也体现了公民的文明素质,更反映了城市的文明程度.在某路口的斑马线路段横穿双向车道,其中,米,在人行绿灯亮时,小刚共用时10秒通过AC,其中通过BC的速度是通过AB的倍,求小刚通过AB的速度.设小刚通过AB的速度为x米/秒,则根据题意列方程为( )
A. B. C. D.
10.关于x的一元二次方程的根的情况,下列说法正确的是( )
A. 实数根的个数由b的值确定 B. 没有实数根
C. 两根互为倒数 D. 若,则两根互为相反数
11.如图,点P在正六边形ABCDEF的对角线BE上移动,以点A为圆心、线段AP的长为半径作弧,交射线AF于点若,则AQ的长可以是( )
A.
B. 3cm
C.
D. 7cm
12.如图1是点P为等边的边AC上一点点P不与点C重合,过点P作于点Q,设,,y与x的函数关系图象如图2所示,下列结论正确的是( )
A. B. 等边三角形ABC的边长为3
C. 当时,BP的长最小 D. y与x的函数关系为:
二、填空题:本题共4小题,每小题3分,共12分。
13.若,则“?”是______.
14.如图是手机支架的侧面示意图,若调整支撑杆的角度,使得,,则直线DE与BC所夹锐角的大小为______.
15.如图,正方形ABCD的顶点都在正方形网格的格点处,已知点,若反比例函数的图象与正方形ABCD有公共点包括边界,则k的整数值有______个.
16.如图,已知,且,,,点D、F分别在BC、AC上滑动.点M是AB的中点,点N是DF的中点,则MN的最小值是______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题7分
如图,容器中装有5个小球,小球上分别标有数字:,0,5,2,现从容器中随机摸出四个小球,对小球上的数字进行运算.
①若摸出的四个小球上分别标有2,,0,,计算:;
②若摸出的四个数字的积不为0,求这四个数字的和;
将摸出的四个小球上的数字按一定顺序填入“□-□-□-□”中的“□”内,计算所得算式的结果,直接写出计算结果的最小值.
18.本小题8分
下面是一道例题及其解答过程的一部分,其中A、B是关于n的多项式.
例:先去括号,再合并同类项:
解:
=…
①直接写出:______,______;
②直接写出:原式的运算结果为______;
若n为任意正整数,试说明的值总能被7整除.
19.本小题9分
为提高在校生消防安全意识,现从某校抽取一部分学生进行消防安全知识检测,男生女生分开进行,将男生成绩绘制成条形统计图其中得4分的人数丢失,女生成绩绘制成扇形统计图,若从参赛的男生中随机抽取一人,抽到得4分的概率为
计算男生得4分的人数,补全条形统计图;
若男生的人数是女生的人数的2倍,男生成绩中位数是a,女生成绩众数是b,求的值;
若扇形图中的和是邻补角,求女生得分为5分的扇形的圆心角度数,并比较此时男生和女生平均成绩的大小.
20.本小题9分
如图,笔直的海岸线l上有A,B两个观测站,A在B的正东方向.有一艘渔船在点P处,从A处测得渔船在北偏西的方向,从B处测得渔船在其东北方向,且测得B,P两点之间的距离为20海里,渔船从点P处沿射线AP的方向航行一段时间后到达点C,此时,从B测得渔船在北偏西的方向.
填空:______度,______度;
求观测站A,B之间的距离结果保留根号;
求点C与点B之间的距离结果保留整数
参考数据:
21.本小题9分
如图,量角器的直径,点A对应刻度,点B对应刻度,AB的中点即量角器的外轮廓所在圆的圆心为点O,点P为AB右下方上一点,弧BP所对应的圆心角为,射线PQ从与PB重合的位置开始,以每秒的速度绕点P逆时针旋转一周,射线PQ与,AB分别相交于点C,点
当点C处的刻度为时,直接写出的度数;
当射线PQ刚好经过点O时.求PQ在量角器上扫过部分的面积;
当射线PQ旋转至与相切时,求射线PQ旋转的时间.
22.本小题9分
如图,已知一次函数的图象经过点,
求这个一次函数;
若点在该函数图象上,连接OC,求的面积;
若点是该函数图象上的一个动点,点D坐标为连接DP,将线段DP绕点D顺时针旋转得到线段DQ,点Q是否能落在第三象限,若能,请直接写出m的取值范围;若不能,请说明理由.
23.本小题10分
消防员正在对一处着火点A进行喷水灭火,水流路线L为抛物线的一部分.建立如图所示的平面直角坐标系,已知消防车上的喷水口B高出地面2m,距离原点的水平距离为6m,着火点A距离点B的水平距离为10m,且点B,A分别位于y轴左右两侧,抛物线L的解析式为其中b,c为常数
写出点B的坐标,并用含b的代数式表示c;
若着火点A高出地面
①求水流恰好经过着火点A时抛物线L的解析式,并求它的对称轴;
②为彻底消除隐患,消防员对距着火点A水平距离1m的范围内继续进行喷水,直接写出抛物线水流路线解析式中b的取值范围包含端点是______,及c的最小值是______.
24.本小题11分
如图1,在平行四边形ABCD中,于点E,且点P从点E出发,沿向终点C运动,设点P在该折线上运动的路径长为,连接
的长为______,当点 P在BC上运动时,EP的最小值为______;
点F是AE的中点,如图2,
①请用无刻度的直尺和圆规过点F作BC的垂线FG,垂足为点保留作图痕迹,不写作法;
②求证:≌;
延长PE到点M,使得,以CE,ME为邻边作平行四边形
①当点P在BC上,平行四边形CEMN对角线EN所在的直线恰好经过点D时,如图3,求x的值;
②当点A落在平行四边形CEMN的边上或内部时,直接写出x的取值范围.
答案和解析
1.A
解:,
故选:
2.C
解:根据题意可知,过点P作直线l的垂线,过点P作直线l的平行线,,
将,代入,可得
故选:
3.A
解:,
,
由数轴可知,该不等式的解集为,
,
解得,
故选:
4.D
解:如图,根据位似中心是位似点连线的交点,可知点P为位似中心,
故选:
5.C
解:
故选:
6.C
解:拿走其中的n个小正方体后,发现该几何体的左视图没有发生变化,可以拿走最左侧的一个和最右侧的两个,则n的最大值为
故选:
7.D
解:原式
当时.原式
故选:
8.C
解:点I是的内心,
,,
,
,
又四边形ABCD内接于,
,
故选:
9.A
解:米,
米.
小刚通过AB的速度为x米/秒,通过BC的速度是通过AB的倍,
小刚通过BC的速度为米/秒.
又小刚共用时10秒通过AC,
故选:
10.D
解:,
此方程有两个不相等的实数根,
当时,方程变形为,解得或,即两根互为相反数,
故选:
11.C
解:如图,过点A作于点,
则由题意可知,,,
,
,,
在中,由勾股定理得,,
在中,由勾股定理得,,
当点P在正六边形ABCDEF的对角线BE上移动时,,
故选:
12.B
解:观察图象得:当时,,此时点P与点A重合,
由题意可得:此时点Q是BC的中点,
,,
此时,
此时,
解得:负值舍去,故A选项错误;
等边三角形ABC的边长为,故B选项正确;
在中,,,
,,
当时,取得最小值,BP长最小,故C选项错误;
,故D选项错误.
故选:
13.3
解:,
“?”是3,
故答案为:
根据幂的乘方法则计算即可.
本题考查了幂的乘方与积的乘方,熟练掌握运算法则是解题的关键.
14.
解:延长DE交BC于F,
,,
故答案为:
15.9
解:点,正方形ABCD的顶点都在正方形网格的格点处,
,
当反比例函数过点D时,,
当反比例函数过点B时,,
满足条件的k的取值范围为,其中共有9个k的整数值.
故答案为:
16.2
解:连接CN,CM,
,,,
,
,
,
点M是AB的中点,点N是DF的中点,,
,,
由三角形三边关系定理得到:,
的最小值是
故答案为:
17.①,②;
①
;
②摸出的四个数字的积不为0,
摸出的四个数字为,5,2,
;
根据有理数的加法法则可知,当摸出的四个小球上的数字为,0,5,2时,计算结果最小,
即
18.①;;②; 证明见解析.
①根据题意可知,,
则,
故答案为:;;
②
故答案为:;
原式
,
即n为任意正整数,的值总能被7整除.
19.6,图见解析;
;
,男生平均成绩>女生平均成绩.
设得4分的人数为x,则,解得,
经检验,是分式方程的解,
补全条形统计图如图,
男生人数为20人,
女生人数为10人,
由题意可知,男生成绩的第10,11个数分别为3和4,
中位数分,
观察扇形统计图可知 分,
;
若扇形图中的和是邻补角,则,即2分,3分所占的比例为,
分所占的比例为,
,
女生得分为5分的扇形的圆心角度数为,
男生平均成绩:分,
女生平均成绩:分,
男生平均成绩>女生平均成绩.
20.30,45;
观测站A,B之间的距离为海里;
点C与点B之间的距离约为27海里.
解:从A处测得点P处渔船在北偏西的方向,
,
从B处测得渔船点P处在其东北方向,从B测得点C渔船在北偏西的方向,
,
,
故答案为:30,45;
如图1,过点P作于D点,则,
在中,,海里,
海里,海里,
在中,,
海里,
海里,
观测站A,B之间的距离为海里;
根据题意,得如图2,过点P作于D点,过点B作,垂足为F,
在中,,,
海里.
在中,,,
海里,
则点C与点B之间的距离约为27海里.
21.; ; 当射线PQ旋转至与相切时,射线PQ旋转的时间为30秒或66秒.
解:的度数为
连接OC,如图,
点C处的刻度为,
,
,
;
连接PO并延长,交于点C,如图,
弧BP所对应的圆心角为,
,
,
在量角器上扫过部分为扇形
,
在量角器上扫过部分的面积为
连接PO,过点P作,如图,
,OP为的半径,
为的切线,
,,
为等边三角形,
,
,
情况一:当PQ旋转至位置时,
射线PQ旋转的角度为,
射线PQ从与PB重合的位置开始,以每秒的速度绕点P逆时针旋转,
射线PQ旋转的时间为秒
情况二:当PQ旋转至位置时,射线PQ转过的角度为,
射线PQ从与PB重合的位置开始,以每秒的速度绕点P逆时针旋转,
射线PQ旋转的时间为秒
综上所述,当射线PQ旋转至与相切时,射线PQ旋转的时间为30秒或66秒.
22.;
12;
点Q能落在第三象限;m的取值范围为;理由见解答过程.
解:已知一次函数的图象经过点,,将点A,点B的坐标分别代入得:
,
解得,
这个一次函数的解析式为;
点在图象上,将点C代入得:
,
解得,
,
的OB边上的高为,
又,
,
的面积为
点Q能落在第三象限;m的取值范围为;理由如下:
解:将点代入一次函数得:,
,
由题意,有以下两个临界位置:
①如图1,当轴时,将线段DP绕点D顺时针旋转得到线段DQ,点Q恰好落在y轴上,
点D坐标为,
此时,
解得;
②如图2,当将线段DP绕点D顺时针旋转得到线段DQ,点Q恰好落在x轴上时,
过点P作轴于点E,
,
点D坐标为,
,
轴,,
,
,
由旋转的性质得:,,
,
,
在和中,
,
≌,
,
,即,
将线段DP绕点D顺时针旋转得到线段DQ,点Q能落在第三象限,此时
23.点B的坐标为,;
①抛物线的解析式为:,对称轴为直线;②,
消防车上的喷水口B高出地面2m,距离原点的水平距离为6m,
点B的坐标为,
抛物线L的解析式为经过点,
,
整理得:;
①着火点A距离点B的水平距离为10m,着火点A高出地面3m,点B的坐标为,
,
,
由得,
抛物线的解析式为:,
水流恰好经过着火点A,
代入得:,
解得:,
,
抛物线的解析式为:,
对称轴为直线,
②消防员对距着火点A水平距离1m的范围内继续进行喷水,,
当抛物线经过点时,
,
解得:;
当抛物线经过点时,
,,
解得:,
综上可得:,
,,
随b的增大而增大,
当时,c取得最小值为,
的最小值为
故答案为:,
24.5;;
①见解析;
②见解析;
①;
②x的取值范围为;理由见解答过程.
解:在平行四边形ABCD中,于点E,且
,
,
解得:,
在直角三角形BCE中,由勾股定理得:,
当时,EP取得最小值,
,即,
解得:,
的最小值为;
故答案为:5;;
①如图2,即为所求;
②由作图知,
,即,
,
,
,
点F是AE的中点,
,
,
≌;
①点P从点E出发,沿向终点C运动,设点P在该折线上运动的路径长为,点P在BC上,平行四边形CEMN对角线EN所在的直线恰好经过点D时,如图3,
由题意得,,,,
,
,,
,
四边形 ABCD是平行四边形,
,,
,
,
,
,
,
,
∽,
,
,
,
,
解得;
②x的取值范围为;理由如下:
当P在BE上时,如图4,
,
,
当时,点A落在 CEMN的边上,
,
解得:,
;
当P在BC上时,如图5,过P作于Q,设MN与直线AB交于H,
,
,
,,,
,,
,
四边形CEMN是平行四边形,
,,
,
,
,
,
∽,
,
,
,
,,
当且时,点A落在 CEMN的边上或内部,
,
解得:,
,
综上所述,当时,点A落在 CEMN的边上或内部.
同课章节目录
