第五单元简易方程同步练习(含解析)人教版数学五年级上册
文档属性
| 名称 | 第五单元简易方程同步练习(含解析)人教版数学五年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 129.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-22 17:42:20 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第五单元简易方程
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.解方程时,等式两边要同时( )。
A.加上12 B.减去12 C.除以12
2.解方程7.2+5x=39.7时,第一步是( )。
A.7.2+5x-7.2=39.7-7.2 B.7.2+5x÷5=39.7÷5 C.7.2+5x-5x=39.7-5x
3.下面的式子中,是方程的( )。
A.45÷9=5 B.y+8 C.x+8<15 D.4y=2
4.下面属于方程的是( )
A.3+x B.4+a=8 C.7+6=13 D.7x
5.如果1.23×a<1.23,则a( )。
A.大于1 B.等于1 C.小于1
6.甲数是乙数的3倍,下面( )算式是对的.
A.甲数×3=乙数 B.乙数+3=甲数 C.乙数×3=甲数
7.下列方程中,与方程1.5+0.6=1.8的解不同的是( )。
A.1.5=1.2 B.15+0.6=18 C.15+6=18 D.15=12
8.下列式子是方程的是( )。
A.3+2=2+3 B.3x=9 C.x+7 D.x-7>5
9.若方程2x+3=7的解与方程ax-5=9的解相同,则a的值为( )。
A.7 B.9 C.2
10.帅帅前几次数学考试的平均成绩是87.5,这一次的校考如果考105分,平均成绩正好是91分,这是帅帅的第( )次数学考试。
A.3 B.4 C.5
二、填空题
11.解时,把( )看成一个整体。
12.等式两边乘( ),或除以( )的数,左右两边仍然相等。
13.=6是方程+3=9的( )。
14.用含有字母的式子表示题目中的数量。
货车每次运货n吨,运了8次,共运货( )吨。
15.用字母表示数写出运算定律,比用文字叙述更( ),也( )应用。
16.如果3a+1.8=7.8,那么1.5a+4=( )。
17.在第19届中国北京科技产业博览会上,一项“中国原创”的重大发明成为世界焦点,这项发明被称为“立体快巴”,也被称为“空中奔跑的巴士”“陆地空客”。普通公交车最大载客a人,“立体快巴”载客量是普通公交车最大载客量的15倍,“立体快巴”最大载客( )人。“立体快巴”的载客量比普通公交车的最大载客量还多1120人,根据上面所述数量关系列出方程是( )。
18.45×(20×61)=(45×20)×61这是应用了( )律。用字母表示:(a×b)×c=( )。
19.说一说下面每个式子所表示的意义.
张师傅每天做a个零件,李师傅每天比张师傅多做8个.
a+8表示的意义是 .
5a表示的意义是 .
20.有4个长方形瓷片拼成一个大正方形(如图),中间空白处是正方形,量得大小正方形边长分别是10厘米和2厘米,你能算出一块瓷片的面积是 平方厘米.
三、判断题
21.4×b=4b.( )
22.所有等式都是方程,所有的方程都是等式。 。
23.a的平方表示2个a相乘,也就是2a。( )
24.已知〇+☆=180,△+☆=180(☆为同一个数),根据等式的性质,两边同时减去☆,由此得到〇△。( )
25.8a+16a=(8+16)a. ( )
四、计算题
26.一个数,先加上6,所得结果再乘8,最后用9去除,结果是32,求这个数?
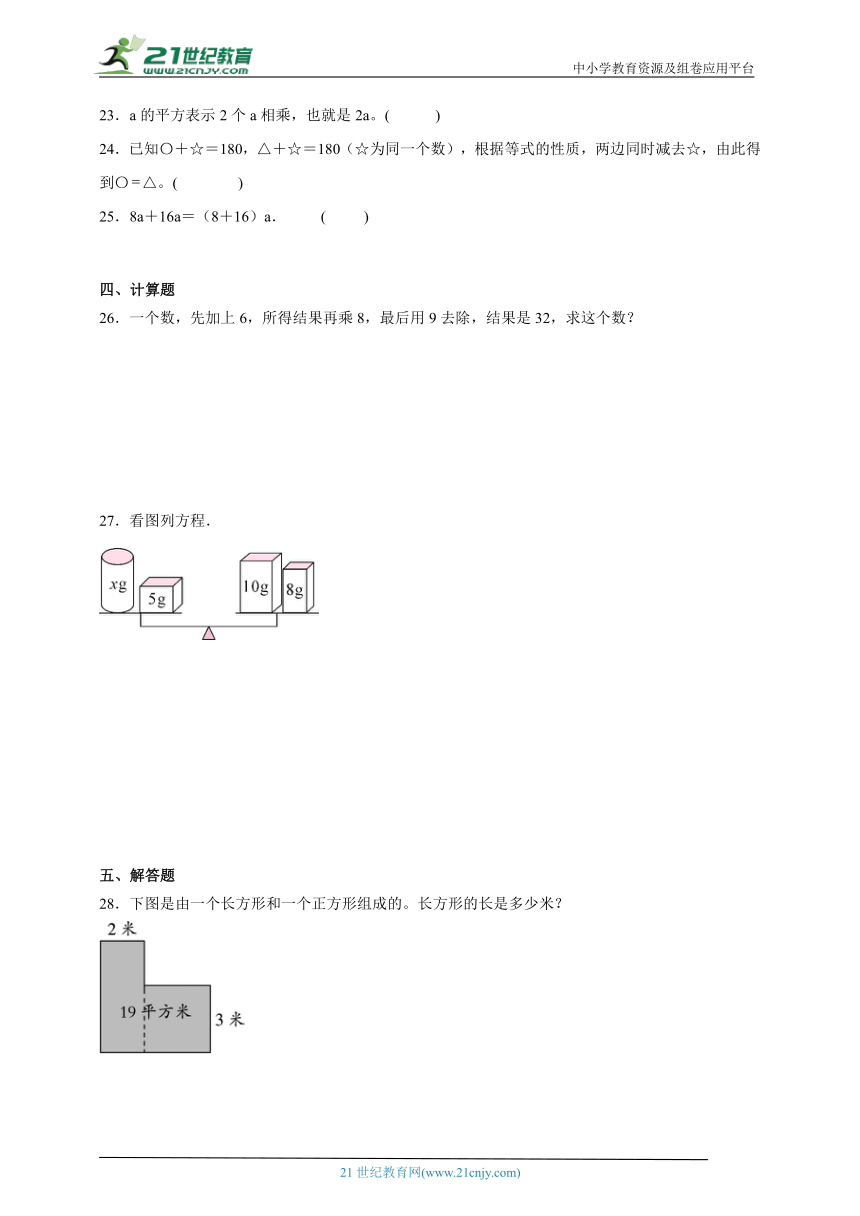
27.看图列方程.
五、解答题
28.下图是由一个长方形和一个正方形组成的。长方形的长是多少米?
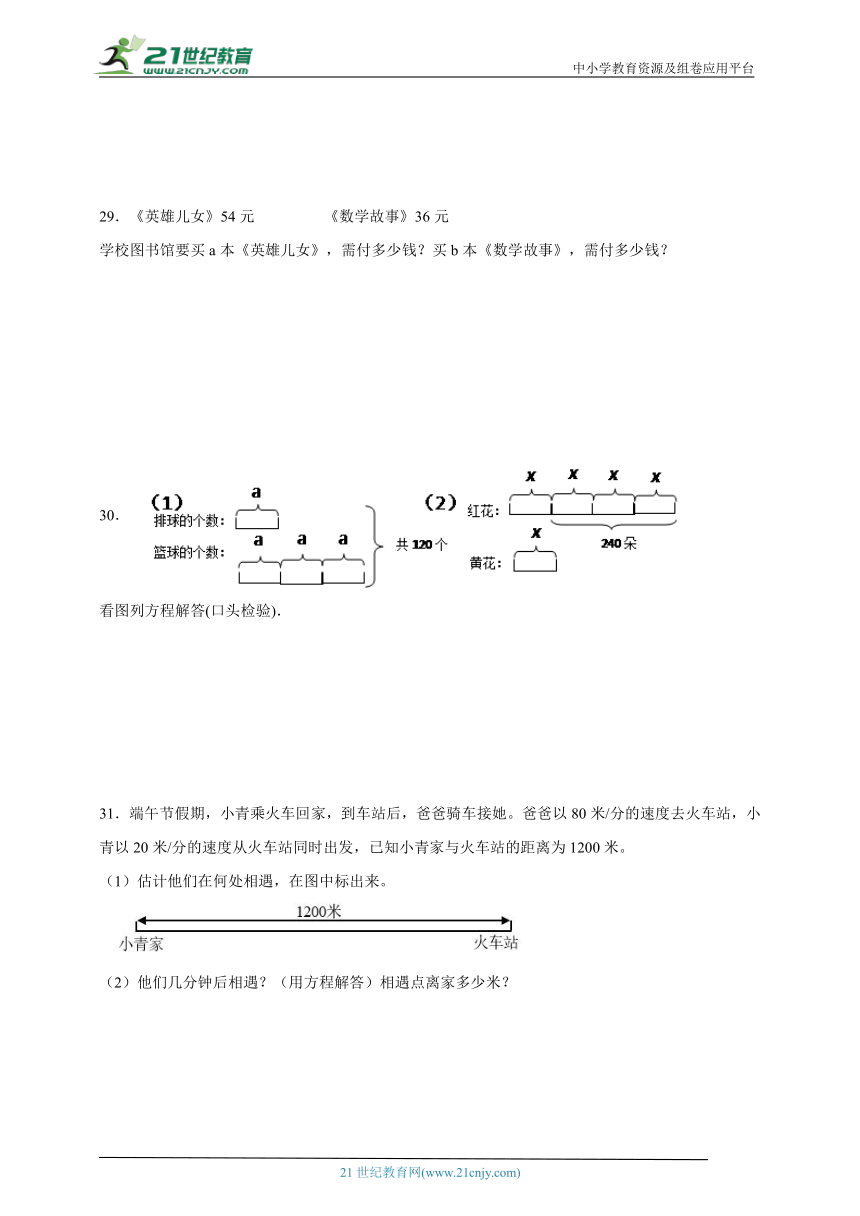
29.《英雄儿女》54元 《数学故事》36元
学校图书馆要买a本《英雄儿女》,需付多少钱?买b本《数学故事》,需付多少钱?
30.
看图列方程解答(口头检验).
31.端午节假期,小青乘火车回家,到车站后,爸爸骑车接她。爸爸以80米/分的速度去火车站,小青以20米/分的速度从火车站同时出发,已知小青家与火车站的距离为1200米。
(1)估计他们在何处相遇,在图中标出来。
(2)他们几分钟后相遇?(用方程解答)相遇点离家多少米?
《第五单元简易方程》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A D B C C B B A C
1.A
【分析】方程左边有一个减去12,要去掉减法,需要用加法。据此解题。
【详解】解方程时,等式两边要同时加上12。
故答案为:A
【点睛】本题考查了解方程,掌握等式的性质1是解题关键。
2.A
【分析】解方程时,先把5x看作一个整体,利用等式的性质1,方程两边同时减去7.2,再利用等式的性质2,方程两边同时除以5,据此解答。
【详解】解方程7.2+5x=39.7时,第一步是方程两边同时减去7.2。
故答案为:A
【点睛】掌握利用等式的性质求方程解的方法是解答题目的关键。
3.D
【分析】含有字母的等式就是方程,据此概念判断各选项中的式子是否是方程即可。
【详解】A.“45÷9=5”中没有未知数,所以它不是方程;
B.“y+8”中没有等号,所以它不是方程;
C.“x+8<15”中没有等号,所以它不是方程;
D.“4y=2”中有未知数有等号,所以它是方程。
故答案为:D
【点睛】本题考查了方程的概念。判断一个式子是否是方程,要看一下两点:①是否是等号;②是否有未知数。
4.B
【详解】略
5.C
【分析】根据因数和积的大小关系进行判断。
A.一个数(0除外)乘大于1的数,积比原来的数大;
B.一个数(0除外)乘1,积等于原来的数;
C.一个数(0除外)乘小于1的数,积比原来的数小。
【详解】A.如果a大于1,那么1.23×a>1.23,不符合题意;
B.如果a等于1,那么1.23×a=1.23,不符合题意;
C.如果a小于1,那么1.23×a<1.23,符合题意。
故答案为:C
6.C
【分析】:根据甲数是乙数的3倍,可知乙数×3=甲数,据此进行选择.
【详解】因为甲数是乙数的3倍;
所以乙数×3=甲数.
故选C.
7.B
【分析】等式的性质1:等式的两边同时加上或减去同一个数,左右两边仍然相等。
等式的性质2:等式的两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
根据等式的性质分别求出原方程和四个选项中方程的解,再比较,得出结论。
【详解】1.5+0.6=1.8
解:1.5+0.6-0.6=1.8-0.6
1.5=1.2
1.5÷1.5=1.2÷1.5
=0.8
A.1.5=1.2
解:1.5÷1.5=1.2÷1.5
=0.8
与方程1.5+0.6=1.8的解相同,不符合题意;
B.15+0.6=18
解:15+0.6-0.6=18-0.6
15=17.4
15÷15=17.4÷15
=1.16
与方程1.5+0.6=1.8的解不同,符合题意;
C.15+6=18
解:15+6-6=18-6
15=12
15÷15=12÷15
=0.8
与方程1.5+0.6=1.8的解相同,不符合题意;
D.15=12
解:15÷15=12÷15
=0.8
与方程1.5+0.6=1.8的解相同,不符合题意。
故答案为:B
【点睛】本题考查根据等式的性质解方程,也可以求出原方程的解,再把方程的解分别代入四个选项的方程左边进行检验,找出与方程的右边不相等的方程即可。
8.B
【分析】含有未知数的等式是方程。据此概念解题即可。
【详解】A.3+2=2+3是等式,不含有未知数,所以不是方程;
B.3x=9既含有未知数又是等式,具备了方程的条件,因此是方程;
C.x+7虽然含有未知数,但它不是等式,也不是方程;
D.x-7>5虽然含有未知数,但它是不等式,不是方程。
故答案为:B
【点睛】本题考查了方程的认识,掌握方程的概念是解题的关键。
9.A
【分析】先求出2x+3=7的解,再把解代入ax-5=9中,即可求出m的值;据此解答。
【详解】由分析可知:
2x+3=7
解:2x+3-3=7-3
2x=4
2x÷2=4÷2
x=2
把x=2代入ax-5=9中
2a-5=9
解:2a-5+5=9+5
2a=14
2a÷2=14÷2
a=7
即若方程2x+3=7的解与方程ax-5=9的解相同,则a的值为7。
故答案为:A
10.C
【分析】假设帅帅前面已经考了x次,这一次是第(x+1)次考试,前面x次的总分是x×87.5分,再加上这一次校考的分数105分,求出总的分数,再除以考试的总次数,等于平均成绩91分,据此列出方程,解方程求出帅帅已经参加的次数,最后加1即可得解。
【详解】解:设帅帅前面已经考了x次。
(87.5×x+105)÷(x+1)=91
87.5x+105=91×(x+1)
87.5x+105=91+91x
91x-87.5x=105-91
3.5x=14
x=14÷3.5
x=4
4+1=5(次)
即这是帅帅的第5次数学考试。
故答案为:C
【点睛】此题的解题关键是弄清题意,把帅帅前面考试的次数设为未知数x,找出题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。
11.
【分析】解时,把看成一个整体,根据等式的性质,在方程两边同时减去2,再在方程两边同时乘5即可求解。
【详解】解时,把看成一个整体。
【点睛】此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去、同时乘或同时除以一个数(0除外),两边仍相等。
12. 同一个数 同一个不为0
【详解】等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
如:20=18+2,20×3=(18+2)×3。
13.解
【分析】等式的性质1:等式的两边同时加上或减去同一个数,左右两边仍然相等。
根据等式的性质1求出方程+3=9的解,据此解答。
【详解】+3=9
解:+3-3=9-3
=6
所以,=6是方程+3=9的解。
14.8n
【分析】共运货的吨数=每次运货数×次数,据此可以解答此题。
【详解】由分析可知,货车每次运货n吨,运了8次,共运货8n吨。
15. 简明易记 便于
【详解】用字母表示数在数学中有不少优势,其中用字母表示数写出运算定律,比用文字叙述更简明易记,也便于应用。
16.7
【分析】根据题意,3a+1.8=7.8,等式的两边同时先减去1.8,然后再同时除以3,求出a的数值,然后再代入1.5a+4求出即可。
【详解】3a+1.8=7.8
解:3a+1.8-1.8=7.8-1.8
3a=6
3a÷3=6÷3
a=2
那么1.5a+4=1.5×2+4=7。
【点睛】本题关键是根据等式的性质求出a的数值,然后代入求解即可。
17. 15a 15a-a=1120
【分析】求一个数的几倍是多少,用乘法计算,即用a乘15即可求出“立体快巴”最大载客的人数;因为“立体快巴”的载客量比普通公交车的最大载客量还多1120人,则可得数量关系:“立体快巴”的载客量-普通公交车的最大载客量=1120,据此填空即可。
【详解】a×15=15a(人)
普通公交车最大载客a人,“立体快巴”载客量是普通公交车最大载客量的15倍,“立体快巴”最大载客15a人。“立体快巴”的载客量比普通公交车的最大载客量还多1120人,根据上面所述数量关系列出方程是15a-a=1120。
18. 乘法结合 a×(b×c)
【分析】根据乘法结合律:三个数相乘,先乘前两个数,或先乘后两个数,积不变,由此进行填空即可。
【详解】45×(20×61)=(45×20)×61这是应用了乘法结合律。用字母表示:(a×b)×c=a×(b×c)。
19. 李师傅每天做零件个数 张师傅5天做零件个数
【详解】由李师傅每天做零件个数=张师傅每天做零件个数+8,可知a+8表示的意义;
由张师傅做零件个数=张师傅每天做零件个数×天数,可知5a表示的意义.
20.24
【详解】试题分析:根据图形观察可得:长方形的长与宽的和等于大正方形的边长10厘米;长与宽的差等于小正方形的边长;由此设长方形的长为x、宽为y,即可得出两个含有x、y的方程,由此利用加减消元的方法即可分别求得x、y的值.
解:设长方形的长为x厘米,宽为y厘米;根据题意可得方程:
x+y=10,①;
x﹣y=2,②;
①+②可得:2x=12,则x=6;
把x=6代入①可得:y=4,
所以长方形的面积为:6×4=24(平方厘米),
答:一块瓷砖的面积为24平方厘米.
故答案为24.
点评:根据图形观察,得出长方形的长和宽与已知的大小正方形的边长的数量关系,是解决本题的关键.
21.√
【详解】略
22.×
【分析】方程是指含有未知数的等式,而等式是指等号两边相等的式子;所以所有的方程都是等式是正确的,但是所有的等式也一定是方程,就是错误的,举例验证即可进行判断。
【详解】所有的方程都是等式,此句正确;
但所有的等式就不一定是方程,如:5×10=25×2,只是等式,不是方程,因为只有含未知数的等式才是方程。
故答案为:×
【点睛】此题考查方程与等式的关系:所有的方程都是等式,但等式不一定是方程,只有含未知数的等式才是方程。
23.×
【分析】根据乘法的意义:a的平方表示2个a相乘,而2a表示2个a相加,据此解答。
【详解】a的平方表示2个a相乘,写成,也就是a2。
而2a表示2个a相加,写成,因此a的平方表示2个a相乘,也就是a2,原题干的说法是错误的。
故答案为:×
【点睛】解答本题的关键是正确区分a2和2a的不同。
24.√
【分析】等式的性质1:等式的两边同时加上或减去同一个数,左右两边仍然相等。
根据等式的性质1,将〇+☆=180和△+☆=180的两边同时减去☆,再比较,得出结论。
【详解】〇+☆=180,两边同时减去☆,即:
〇+☆-☆=180-☆
得〇=180-☆
△+☆=180,两边同时减去☆,即:
△+☆-☆=180-☆
得△=180-☆
由此得到〇△。
原题说法正确。
故答案为:√
【点睛】本题考查等式的性质1的应用。
25.√
【解析】略
26.30
【分析】假设这个数是x,根据题目中的数量关系:(这个数+6)×8÷9=32,代入未知数,列出方程,解方程即可求出这个数。
【详解】解:设这个数是x,
(x+6)×8÷9=32
(x+6)×8÷9×9=32×9
(x+6)×8=288
(x+6)×8÷8=288÷8
x+6=36
x+6-6=36-6
x=30
即这个数是30。
27.x+5=10+8
【解析】略
28.5米
【分析】根据题图可知,“长方形的面积+正方形的面积=组合图形的面积”,据此列方程解答即可。
【详解】解:设长方形的长为x米。
2x+3×3=19
2x+9=19
2x+9-9=19-9
2x=10
2x÷2=10÷2
x=5
答:长方形的长是5米。
【点睛】明确题目中存在的等量关系是解答本题的关键。
29.54a元;36b元
【分析】用一本《英雄儿女》的价钱乘a求出买a本《英雄儿女》需付的金额;用一本《数学故事》的价钱乘b求出买b本《数学故事》需付的金额;据此解答。
【详解】54×a=54a(元)
36×b=36b(元)
答:学校图书馆要买a本《英雄儿女》,需付54a元;买b本《数学故事》,需付36b元。
【点睛】熟练掌握单价×数量=总价,是解答此题的关键。
30.(1)30;(2)80
【详解】(1)解:a+3a=120 (2) 4x-x=240
(3+1)a=120 (4-1)x=240
4a÷4=120÷4 3x÷3=240÷3
a=30 x=80
31.(1)见详解
(2)960米
【分析】(1)由于爸爸的速度快,小青的速度比较慢,而且爸爸比小青的速度快得多,所以在过中点,离火车站近点的地方相遇,标注合理即可。
(2)可以设他们x分钟相遇,小青每分钟走的路程×相遇时间+爸爸每分钟走的路程×时间=1200,据此即可列方程,再根据等式的性质解方程即可,再用爸爸每分钟走的路程×时间即可求出相遇点离家多少米。。
【详解】(1)如下图所示:
(2)解:设他们x分钟后相遇。
80x+20x=1200
100x=1200
100x÷100=1200÷100
x=12
12×80=960(米)
答:相遇点离家960米。
【点睛】本题主要考查列方程解一个未知数的题目以及相遇问题的公式,熟练掌握它的公式并灵活运用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五单元简易方程
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.解方程时,等式两边要同时( )。
A.加上12 B.减去12 C.除以12
2.解方程7.2+5x=39.7时,第一步是( )。
A.7.2+5x-7.2=39.7-7.2 B.7.2+5x÷5=39.7÷5 C.7.2+5x-5x=39.7-5x
3.下面的式子中,是方程的( )。
A.45÷9=5 B.y+8 C.x+8<15 D.4y=2
4.下面属于方程的是( )
A.3+x B.4+a=8 C.7+6=13 D.7x
5.如果1.23×a<1.23,则a( )。
A.大于1 B.等于1 C.小于1
6.甲数是乙数的3倍,下面( )算式是对的.
A.甲数×3=乙数 B.乙数+3=甲数 C.乙数×3=甲数
7.下列方程中,与方程1.5+0.6=1.8的解不同的是( )。
A.1.5=1.2 B.15+0.6=18 C.15+6=18 D.15=12
8.下列式子是方程的是( )。
A.3+2=2+3 B.3x=9 C.x+7 D.x-7>5
9.若方程2x+3=7的解与方程ax-5=9的解相同,则a的值为( )。
A.7 B.9 C.2
10.帅帅前几次数学考试的平均成绩是87.5,这一次的校考如果考105分,平均成绩正好是91分,这是帅帅的第( )次数学考试。
A.3 B.4 C.5
二、填空题
11.解时,把( )看成一个整体。
12.等式两边乘( ),或除以( )的数,左右两边仍然相等。
13.=6是方程+3=9的( )。
14.用含有字母的式子表示题目中的数量。
货车每次运货n吨,运了8次,共运货( )吨。
15.用字母表示数写出运算定律,比用文字叙述更( ),也( )应用。
16.如果3a+1.8=7.8,那么1.5a+4=( )。
17.在第19届中国北京科技产业博览会上,一项“中国原创”的重大发明成为世界焦点,这项发明被称为“立体快巴”,也被称为“空中奔跑的巴士”“陆地空客”。普通公交车最大载客a人,“立体快巴”载客量是普通公交车最大载客量的15倍,“立体快巴”最大载客( )人。“立体快巴”的载客量比普通公交车的最大载客量还多1120人,根据上面所述数量关系列出方程是( )。
18.45×(20×61)=(45×20)×61这是应用了( )律。用字母表示:(a×b)×c=( )。
19.说一说下面每个式子所表示的意义.
张师傅每天做a个零件,李师傅每天比张师傅多做8个.
a+8表示的意义是 .
5a表示的意义是 .
20.有4个长方形瓷片拼成一个大正方形(如图),中间空白处是正方形,量得大小正方形边长分别是10厘米和2厘米,你能算出一块瓷片的面积是 平方厘米.
三、判断题
21.4×b=4b.( )
22.所有等式都是方程,所有的方程都是等式。 。
23.a的平方表示2个a相乘,也就是2a。( )
24.已知〇+☆=180,△+☆=180(☆为同一个数),根据等式的性质,两边同时减去☆,由此得到〇△。( )
25.8a+16a=(8+16)a. ( )
四、计算题
26.一个数,先加上6,所得结果再乘8,最后用9去除,结果是32,求这个数?
27.看图列方程.
五、解答题
28.下图是由一个长方形和一个正方形组成的。长方形的长是多少米?
29.《英雄儿女》54元 《数学故事》36元
学校图书馆要买a本《英雄儿女》,需付多少钱?买b本《数学故事》,需付多少钱?
30.
看图列方程解答(口头检验).
31.端午节假期,小青乘火车回家,到车站后,爸爸骑车接她。爸爸以80米/分的速度去火车站,小青以20米/分的速度从火车站同时出发,已知小青家与火车站的距离为1200米。
(1)估计他们在何处相遇,在图中标出来。
(2)他们几分钟后相遇?(用方程解答)相遇点离家多少米?
《第五单元简易方程》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A D B C C B B A C
1.A
【分析】方程左边有一个减去12,要去掉减法,需要用加法。据此解题。
【详解】解方程时,等式两边要同时加上12。
故答案为:A
【点睛】本题考查了解方程,掌握等式的性质1是解题关键。
2.A
【分析】解方程时,先把5x看作一个整体,利用等式的性质1,方程两边同时减去7.2,再利用等式的性质2,方程两边同时除以5,据此解答。
【详解】解方程7.2+5x=39.7时,第一步是方程两边同时减去7.2。
故答案为:A
【点睛】掌握利用等式的性质求方程解的方法是解答题目的关键。
3.D
【分析】含有字母的等式就是方程,据此概念判断各选项中的式子是否是方程即可。
【详解】A.“45÷9=5”中没有未知数,所以它不是方程;
B.“y+8”中没有等号,所以它不是方程;
C.“x+8<15”中没有等号,所以它不是方程;
D.“4y=2”中有未知数有等号,所以它是方程。
故答案为:D
【点睛】本题考查了方程的概念。判断一个式子是否是方程,要看一下两点:①是否是等号;②是否有未知数。
4.B
【详解】略
5.C
【分析】根据因数和积的大小关系进行判断。
A.一个数(0除外)乘大于1的数,积比原来的数大;
B.一个数(0除外)乘1,积等于原来的数;
C.一个数(0除外)乘小于1的数,积比原来的数小。
【详解】A.如果a大于1,那么1.23×a>1.23,不符合题意;
B.如果a等于1,那么1.23×a=1.23,不符合题意;
C.如果a小于1,那么1.23×a<1.23,符合题意。
故答案为:C
6.C
【分析】:根据甲数是乙数的3倍,可知乙数×3=甲数,据此进行选择.
【详解】因为甲数是乙数的3倍;
所以乙数×3=甲数.
故选C.
7.B
【分析】等式的性质1:等式的两边同时加上或减去同一个数,左右两边仍然相等。
等式的性质2:等式的两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
根据等式的性质分别求出原方程和四个选项中方程的解,再比较,得出结论。
【详解】1.5+0.6=1.8
解:1.5+0.6-0.6=1.8-0.6
1.5=1.2
1.5÷1.5=1.2÷1.5
=0.8
A.1.5=1.2
解:1.5÷1.5=1.2÷1.5
=0.8
与方程1.5+0.6=1.8的解相同,不符合题意;
B.15+0.6=18
解:15+0.6-0.6=18-0.6
15=17.4
15÷15=17.4÷15
=1.16
与方程1.5+0.6=1.8的解不同,符合题意;
C.15+6=18
解:15+6-6=18-6
15=12
15÷15=12÷15
=0.8
与方程1.5+0.6=1.8的解相同,不符合题意;
D.15=12
解:15÷15=12÷15
=0.8
与方程1.5+0.6=1.8的解相同,不符合题意。
故答案为:B
【点睛】本题考查根据等式的性质解方程,也可以求出原方程的解,再把方程的解分别代入四个选项的方程左边进行检验,找出与方程的右边不相等的方程即可。
8.B
【分析】含有未知数的等式是方程。据此概念解题即可。
【详解】A.3+2=2+3是等式,不含有未知数,所以不是方程;
B.3x=9既含有未知数又是等式,具备了方程的条件,因此是方程;
C.x+7虽然含有未知数,但它不是等式,也不是方程;
D.x-7>5虽然含有未知数,但它是不等式,不是方程。
故答案为:B
【点睛】本题考查了方程的认识,掌握方程的概念是解题的关键。
9.A
【分析】先求出2x+3=7的解,再把解代入ax-5=9中,即可求出m的值;据此解答。
【详解】由分析可知:
2x+3=7
解:2x+3-3=7-3
2x=4
2x÷2=4÷2
x=2
把x=2代入ax-5=9中
2a-5=9
解:2a-5+5=9+5
2a=14
2a÷2=14÷2
a=7
即若方程2x+3=7的解与方程ax-5=9的解相同,则a的值为7。
故答案为:A
10.C
【分析】假设帅帅前面已经考了x次,这一次是第(x+1)次考试,前面x次的总分是x×87.5分,再加上这一次校考的分数105分,求出总的分数,再除以考试的总次数,等于平均成绩91分,据此列出方程,解方程求出帅帅已经参加的次数,最后加1即可得解。
【详解】解:设帅帅前面已经考了x次。
(87.5×x+105)÷(x+1)=91
87.5x+105=91×(x+1)
87.5x+105=91+91x
91x-87.5x=105-91
3.5x=14
x=14÷3.5
x=4
4+1=5(次)
即这是帅帅的第5次数学考试。
故答案为:C
【点睛】此题的解题关键是弄清题意,把帅帅前面考试的次数设为未知数x,找出题中数量间的相等关系,列出包含x的等式,解方程得到最终的结果。
11.
【分析】解时,把看成一个整体,根据等式的性质,在方程两边同时减去2,再在方程两边同时乘5即可求解。
【详解】解时,把看成一个整体。
【点睛】此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去、同时乘或同时除以一个数(0除外),两边仍相等。
12. 同一个数 同一个不为0
【详解】等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
如:20=18+2,20×3=(18+2)×3。
13.解
【分析】等式的性质1:等式的两边同时加上或减去同一个数,左右两边仍然相等。
根据等式的性质1求出方程+3=9的解,据此解答。
【详解】+3=9
解:+3-3=9-3
=6
所以,=6是方程+3=9的解。
14.8n
【分析】共运货的吨数=每次运货数×次数,据此可以解答此题。
【详解】由分析可知,货车每次运货n吨,运了8次,共运货8n吨。
15. 简明易记 便于
【详解】用字母表示数在数学中有不少优势,其中用字母表示数写出运算定律,比用文字叙述更简明易记,也便于应用。
16.7
【分析】根据题意,3a+1.8=7.8,等式的两边同时先减去1.8,然后再同时除以3,求出a的数值,然后再代入1.5a+4求出即可。
【详解】3a+1.8=7.8
解:3a+1.8-1.8=7.8-1.8
3a=6
3a÷3=6÷3
a=2
那么1.5a+4=1.5×2+4=7。
【点睛】本题关键是根据等式的性质求出a的数值,然后代入求解即可。
17. 15a 15a-a=1120
【分析】求一个数的几倍是多少,用乘法计算,即用a乘15即可求出“立体快巴”最大载客的人数;因为“立体快巴”的载客量比普通公交车的最大载客量还多1120人,则可得数量关系:“立体快巴”的载客量-普通公交车的最大载客量=1120,据此填空即可。
【详解】a×15=15a(人)
普通公交车最大载客a人,“立体快巴”载客量是普通公交车最大载客量的15倍,“立体快巴”最大载客15a人。“立体快巴”的载客量比普通公交车的最大载客量还多1120人,根据上面所述数量关系列出方程是15a-a=1120。
18. 乘法结合 a×(b×c)
【分析】根据乘法结合律:三个数相乘,先乘前两个数,或先乘后两个数,积不变,由此进行填空即可。
【详解】45×(20×61)=(45×20)×61这是应用了乘法结合律。用字母表示:(a×b)×c=a×(b×c)。
19. 李师傅每天做零件个数 张师傅5天做零件个数
【详解】由李师傅每天做零件个数=张师傅每天做零件个数+8,可知a+8表示的意义;
由张师傅做零件个数=张师傅每天做零件个数×天数,可知5a表示的意义.
20.24
【详解】试题分析:根据图形观察可得:长方形的长与宽的和等于大正方形的边长10厘米;长与宽的差等于小正方形的边长;由此设长方形的长为x、宽为y,即可得出两个含有x、y的方程,由此利用加减消元的方法即可分别求得x、y的值.
解:设长方形的长为x厘米,宽为y厘米;根据题意可得方程:
x+y=10,①;
x﹣y=2,②;
①+②可得:2x=12,则x=6;
把x=6代入①可得:y=4,
所以长方形的面积为:6×4=24(平方厘米),
答:一块瓷砖的面积为24平方厘米.
故答案为24.
点评:根据图形观察,得出长方形的长和宽与已知的大小正方形的边长的数量关系,是解决本题的关键.
21.√
【详解】略
22.×
【分析】方程是指含有未知数的等式,而等式是指等号两边相等的式子;所以所有的方程都是等式是正确的,但是所有的等式也一定是方程,就是错误的,举例验证即可进行判断。
【详解】所有的方程都是等式,此句正确;
但所有的等式就不一定是方程,如:5×10=25×2,只是等式,不是方程,因为只有含未知数的等式才是方程。
故答案为:×
【点睛】此题考查方程与等式的关系:所有的方程都是等式,但等式不一定是方程,只有含未知数的等式才是方程。
23.×
【分析】根据乘法的意义:a的平方表示2个a相乘,而2a表示2个a相加,据此解答。
【详解】a的平方表示2个a相乘,写成,也就是a2。
而2a表示2个a相加,写成,因此a的平方表示2个a相乘,也就是a2,原题干的说法是错误的。
故答案为:×
【点睛】解答本题的关键是正确区分a2和2a的不同。
24.√
【分析】等式的性质1:等式的两边同时加上或减去同一个数,左右两边仍然相等。
根据等式的性质1,将〇+☆=180和△+☆=180的两边同时减去☆,再比较,得出结论。
【详解】〇+☆=180,两边同时减去☆,即:
〇+☆-☆=180-☆
得〇=180-☆
△+☆=180,两边同时减去☆,即:
△+☆-☆=180-☆
得△=180-☆
由此得到〇△。
原题说法正确。
故答案为:√
【点睛】本题考查等式的性质1的应用。
25.√
【解析】略
26.30
【分析】假设这个数是x,根据题目中的数量关系:(这个数+6)×8÷9=32,代入未知数,列出方程,解方程即可求出这个数。
【详解】解:设这个数是x,
(x+6)×8÷9=32
(x+6)×8÷9×9=32×9
(x+6)×8=288
(x+6)×8÷8=288÷8
x+6=36
x+6-6=36-6
x=30
即这个数是30。
27.x+5=10+8
【解析】略
28.5米
【分析】根据题图可知,“长方形的面积+正方形的面积=组合图形的面积”,据此列方程解答即可。
【详解】解:设长方形的长为x米。
2x+3×3=19
2x+9=19
2x+9-9=19-9
2x=10
2x÷2=10÷2
x=5
答:长方形的长是5米。
【点睛】明确题目中存在的等量关系是解答本题的关键。
29.54a元;36b元
【分析】用一本《英雄儿女》的价钱乘a求出买a本《英雄儿女》需付的金额;用一本《数学故事》的价钱乘b求出买b本《数学故事》需付的金额;据此解答。
【详解】54×a=54a(元)
36×b=36b(元)
答:学校图书馆要买a本《英雄儿女》,需付54a元;买b本《数学故事》,需付36b元。
【点睛】熟练掌握单价×数量=总价,是解答此题的关键。
30.(1)30;(2)80
【详解】(1)解:a+3a=120 (2) 4x-x=240
(3+1)a=120 (4-1)x=240
4a÷4=120÷4 3x÷3=240÷3
a=30 x=80
31.(1)见详解
(2)960米
【分析】(1)由于爸爸的速度快,小青的速度比较慢,而且爸爸比小青的速度快得多,所以在过中点,离火车站近点的地方相遇,标注合理即可。
(2)可以设他们x分钟相遇,小青每分钟走的路程×相遇时间+爸爸每分钟走的路程×时间=1200,据此即可列方程,再根据等式的性质解方程即可,再用爸爸每分钟走的路程×时间即可求出相遇点离家多少米。。
【详解】(1)如下图所示:
(2)解:设他们x分钟后相遇。
80x+20x=1200
100x=1200
100x÷100=1200÷100
x=12
12×80=960(米)
答:相遇点离家960米。
【点睛】本题主要考查列方程解一个未知数的题目以及相遇问题的公式,熟练掌握它的公式并灵活运用。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
